| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Un sistem de ecuatii liniare in care numarul ecuatiilor, m, este mai mare decat numarul necunoscutelor, n, este un sistem supradeterminat.
Forma generala a unui astfel de sistem este data de:
![]() (69)
(69)
unde:
![]() (70)
(70)
este matricea sistemului.
Un astfel de sistem, din punctul de vedere al algebrei clasice, nu are solutie, deci el nu prezinta interes.
In cadrul solutionarii unei probleme tehnice pot apare astfel de sisteme de ecuatii. Un exemplu ar fi acela in care, pentru determinarea unui anumit numar de parametri, n, sa se efectueze un numar mult mai mare de masuratori, m, nu insa suficient de precise.
O alta situatie in care este necesara gasirea unei solutii pentru un astfel de sistem este aceea a rezolvarii sistemelor liniare omogene, asa cum se va vedea in paragraful urmator.
Deoarece sistemul (69) nu are o solutie, se pune problema determinarii unui vector solutie X astfel incat AX sa fie 'cat mai aproape posibil de b'.
Notam:
![]() (71)
(71)
Vectorul R este vectorul reziduu. Se cauta vectorul X astfel incat
![]() sa fie
minima.
sa fie
minima.
Componentele vectorului reziduu au expresiile:
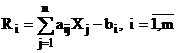 . (72)
. (72)
Se determina componentele ![]() astfel incat suma
astfel incat suma
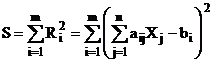 (73)
(73)
sa aiba o valoare minima.
Conditia necesara de extrem este de forma:
![]() (74)
(74)
ea reprezentand un sistem de n ecuatii liniare cu n necunoscute.
Se poate scrie:
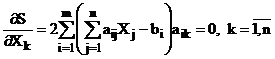 . (75)
. (75)
Rescriind sistemul obtinem:
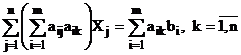 (76)
(76)
Fie ![]() transpusa matricei A, avand elementele:
transpusa matricei A, avand elementele:
![]() (77)
(77)
Tinand cont de (77), relatia (76) se poate scrie sub forma:
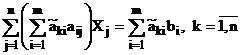 . (78)
. (78)
Tinand cont de expresia produsului ![]() vom avea:
vom avea:
![]() (79)
(79)
deci un sistem de n ecuatii cu n necunoscute.
Daca ![]() sunt vectorii
coloana ai matricei A, avand elementele
sunt vectorii
coloana ai matricei A, avand elementele ![]() , atunci sistemul (79) se mai poate scrie:
, atunci sistemul (79) se mai poate scrie:
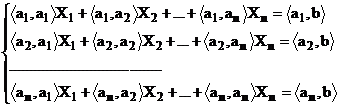 (80)
(80)
unde ![]() reprezinta
produsul scalar dintre vectorii coloana
reprezinta
produsul scalar dintre vectorii coloana ![]() si
si ![]() ai matricei A.
Sistemul avand o matrice patratica poate fi rezolvat numeric printr-o
metoda expusa anterior.
ai matricei A.
Sistemul avand o matrice patratica poate fi rezolvat numeric printr-o
metoda expusa anterior.
Este simplu de aratat ca vectorul R = AX - b este ortogonal oricarui vector Ax, pentru orice x.
Pentru aceasta se face produsul scalar ![]() cu reziduul R:
cu reziduul R:
![]() . (81)
. (81)
Tinand cont ca:
![]() , (82)
, (82)
se poate scrie ca:
![]() (83)
(83)
Rezulta ca pseudo-solutia X a sistemului (69) este obtinuta astfel incat vectorul AX este proiectia vectorului b in spatiul generat de vectorii Ax.
Un sistem de n ecuatii neliniare cu n necunoscute este de forma:
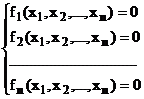 . (94)
. (94)
Folosind o notatie vectoriala, sistemul poate fi pus sub forma:
![]() (95)
(95)
unde:
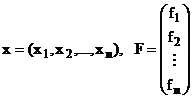 . (96)
. (96)
Se pune sistemul (95)
intr-o forma vectoriala echivalenta, ![]() , evidentiind in cadrul fiecarei ecuatii din (95),
in partea stanga a semnului egal, componenta
, evidentiind in cadrul fiecarei ecuatii din (95),
in partea stanga a semnului egal, componenta ![]() . In aceste conditii sistemul echivalent cu sistemul
initial este
. In aceste conditii sistemul echivalent cu sistemul
initial este ![]() ,
, ![]() fiind componentele
vectorului G.
fiind componentele
vectorului G.
Consideram o
aproximatie initiala ![]() a solutiei
sistemului.
a solutiei
sistemului.
Se utilizeaza relatia de recurenta:
![]() (97)
(97)
sau, pe componente:
![]() . (98)
. (98)
Sirul ![]() este convergent
catre solutia xR a sistemului daca
este convergent
catre solutia xR a sistemului daca ![]() este suficient de
apropiat de
este suficient de
apropiat de ![]() si daca, in
vecinatatea lui
si daca, in
vecinatatea lui ![]() , este indeplinita conditia:
, este indeplinita conditia:
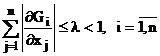 . (99)
. (99)
Se poate arata ca limita sirului de vectori ![]() este chiar
solutia sistemului,
este chiar
solutia sistemului, ![]() .
.
Avem:
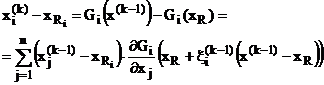 (100)
(100)
unde: ![]() .
.
Tinand seama de conditia de convergenta obtinem:
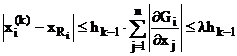 (101)
(101)
unde:
![]() (102)
(102)
Dand valori lui k in relatia (101), putem scrie ca:
![]() . (103)
. (103)
Trecand la limita in aceasta ultima relatie si tinand cont ca l este subunitar, rezulta ca:
![]() (104)
(104)
deci metoda Jacobi este convergenta.
Limita sirului de vectori ![]() este chiar
solutia sistemului,
este chiar
solutia sistemului, ![]() .
.
Consideram
sistemul (95) si presupunem ca intr-o vecinatate V din domeniul
de definitie al lui F exista o solutie unica ![]() , adica
, adica ![]() .
.
Notam:
 (105)
(105)
matricea Jacobiana a sistemului.
Presupunand ca ![]() si
si ![]() sunt continue in
vecinatatea V si ca:
sunt continue in
vecinatatea V si ca:
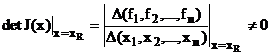 (106)
(106)
rezulta ca F este o transformare regulata in
vecinatatea V a solutiei ![]() si ca
exista transformarea inversa, tot o transformare regulata.
si ca
exista transformarea inversa, tot o transformare regulata.
Mai rezulta
ca ![]() este diferita de
matricea nula intr-o vecinatate a lui
este diferita de
matricea nula intr-o vecinatate a lui ![]() datorita
presupunerilor de continuitate facute asupra derivatelor partiale.
datorita
presupunerilor de continuitate facute asupra derivatelor partiale.
Prin analogie cu functia de iterare a lui Newton din cadrul ecuatiilor cu o singura necunoscuta, in cadrul sistemelor de ecuatii neliniare functia de iterare va avea forma vectoriala:
![]() (107)
(107)
iar sirul de iterare va fi:
![]() (108)
(108)
vectorul ![]() fiind aproximatia
initiala pentru solutia sistemului.
fiind aproximatia
initiala pentru solutia sistemului.
Se poate considera o
alta forma vectoriala a relatiei de recurenta
care sa nu mai contina pe ![]() si anume cea
obtinuta prin inmultirea relatiei (108) la stanga cu
[J(x)]:
si anume cea
obtinuta prin inmultirea relatiei (108) la stanga cu
[J(x)]:
![]() . (109)
. (109)
In practica, este mai utila scrierea sirului de iterare pe componente, sub forma:
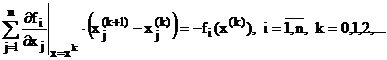 . (110)
. (110)
Aceste relatii reprezinta un sistem de n ecuatii liniare cu n necunoscute, necunoscutele fiind:
![]() . (111)
. (111)
Conditia de convergenta a metodei este data de teorema lui Kantorovich:
Daca in sfera inchisa:
![]() (112)
(112)
sunt satisfacute conditiile:
matricea functionala 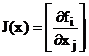 are in
are in ![]() o inversa
o inversa ![]() cu proprietatea
cu proprietatea ![]() ;
;
![]() ;
;
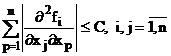 si
si ![]() ;
;
Constantele ![]() satisfac inegalitatea
satisfac inegalitatea ![]() , atunci, pentru aproximatie initiala
, atunci, pentru aproximatie initiala ![]() , sirul iterativ definit de:
, sirul iterativ definit de:
![]()
este convergent catre solutia ![]() .
.
Cap. 4. Valori proprii si vectori proprii
Introducere
Calculul valorilor proprii si a vectorilor proprii pentru matrice patratice constituie probleme frecvent intalnite si de aceea, cunoasterea unor metode numerice de calcul pentru aceste elemente este binevenita.
Este important aici sa reamintim notiunile de baza legate de vectori si valori proprii.
Se considera o matrice A, reala, patratica, de ordin n. Un numar lIC se numeste valoare proprie a matricei A daca exista un vector nenul X astfel incat:
![]() . (4.1)
. (4.1)
Vectorul X se numeste vector propriu asociat valorii proprii l
Daca I este matricea unitate de ordin n, ecuatia (4.1) poate fi pusa sub forma:
![]() (4.2)
(4.2)
Aceasta relatie reprezinta un sistem omogen de ecuatii liniare care nu poate avea o solutie X nenula decat daca:
![]() , (4.3)
, (4.3)
adica:
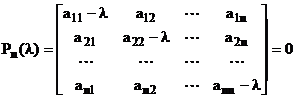 . (4.4)
. (4.4)
Acest determinant
este un polinom de grad n in l, ![]() , care poseda n radacini
, care poseda n radacini ![]() , reale (simple sau multiple) sau complexe.
, reale (simple sau multiple) sau complexe.
![]() se numeste polinom caracteristic iar ecuatia
se numeste polinom caracteristic iar ecuatia![]() = 0 poarta numele de ecuatie caracteristica.
= 0 poarta numele de ecuatie caracteristica.
Fie p numarul valorilor proprii distincte.
Acestora le corespunde un numar p de vectori proprii liniar independenti care pot fi completati cu un numar (n-p) de alti vectori pana la o baza in spatiul vectorial din care face parte A.
Se stie ca
un determinant ramane nemodificat daca i se transforma liniile
in coloane. Ca urmare, daca notam cu ![]() transpusa matricei A,
avem:
transpusa matricei A,
avem:
![]() (4.5)
(4.5)
deci A si ![]() au aceleasi
valori proprii.
au aceleasi
valori proprii.
Fie ![]() si
si ![]() vectorii proprii
pentru A si
vectorii proprii
pentru A si ![]() care corespund valorii
proprii
care corespund valorii
proprii ![]() .
.
Vom avea, prin definitie:
![]() si
si ![]() . (4.6)
. (4.6)
Scriind aceste
relatii pentru doua valori proprii distincte, ![]() . Tinand cont de faptul ca
. Tinand cont de faptul ca ![]() , se poate scrie:
, se poate scrie:
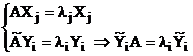 . (4.7)
. (4.7)
Daca in (4.7)
se inmulteste prima relatie la stanga cu ![]() iar a doua la dreapta
cu
iar a doua la dreapta
cu ![]() si apoi se scad,
se obtine:
si apoi se scad,
se obtine:
![]() . (4.8)
. (4.8)
Deoarece s-au considerat valorile proprii li si lj distincte, rezulta ca avem:
![]() . (4.9)
. (4.9)
Se poate spune
ca daca ![]() este un vector propriu
pentru A ce corespunde valorii proprii
este un vector propriu
pentru A ce corespunde valorii proprii ![]() iar
iar ![]() este vectorul propriu al matricei
este vectorul propriu al matricei ![]() ce corespunde valorii
proprii
ce corespunde valorii
proprii ![]() , atunci
, atunci ![]() si
si ![]() sunt vectori
ortogonali daca
sunt vectori
ortogonali daca ![]() .
.
Inainte de a prezenta algoritmul de calcul pentru valorile proprii si vectorii proprii pentru o matrice reala A, este important sa fie facuta o localizare a valorilor proprii. (Teorema lui Gerschgorin):
Fiecare valoare
proprie a matricei A se gaseste in cel putin un disc circular cu
centrul in ![]() si de raza
si de raza
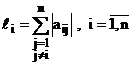 sau
sau 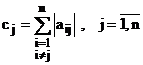 . (4.10)
. (4.10)
Se poate afirma ca toate valorile proprii ale lui A se gasesc in reuniunea discurilor
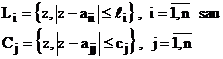 . (4.11)
. (4.11)
Avand k discuri Gerschgorin care formeaza un domeniu compact care este izolat, atunci k valori proprii ale lui A se gasesc in acest domeniu. Un disc izolat contine exact o valoare proprie.
Daca in linia i
a lui A numai elementul ![]() este nenul, atunci acest element este valoare proprie pentru
A.
este nenul, atunci acest element este valoare proprie pentru
A.
Prin aceste metode se pot determina valorile proprii ale matricei A fara a apela la polinomul caracteristic.
Se considera in
cadrul acestei metode ca toate
valorile proprii ![]() ale matricei A, sunt
distincte astfel incat vectorii proprii corespunzatori
ale matricei A, sunt
distincte astfel incat vectorii proprii corespunzatori ![]() formeaza o
baza in spatiul vectorial al matricei A.
formeaza o
baza in spatiul vectorial al matricei A.
Fie V un vector
oarecare. El se poate scrie ca o combinatie liniara a vectorilor ![]() liniar
independenti:
liniar
independenti:
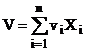 . (4.21)
. (4.21)
Inmultind la
stanga cu A si tinand cont de faptul ca ![]() sunt vectori proprii
se poate scrie:
sunt vectori proprii
se poate scrie:
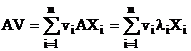 (4.22)
(4.22)
sau, din aproape in aproape:
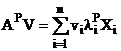 . (4.23)
. (4.23)
Daca:
![]() (4.24)
(4.24)
putem scrie:
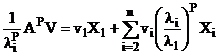 . (4.25)
. (4.25)
Trecand la
limita in relatia (4.25), tinand cont ca ![]() , se obtine:
, se obtine:
![]() (4.26)
(4.26)
sau, altfel scris:
![]() . (4.27)
. (4.27)
Rezulta ca sirul de vectori AV,A2V,, tinde catre vectorul propriu v1X1.
In practica, daca l este suficient de mare, normele vectorilor:
![]() (4.28)
(4.28)
pot creste foarte mult, depasind posibilitatile de calcul. De aceea, la trecerea de la un pas la celalalt se reduce norma vectorului curent la unitate prin impartirea tuturor componentelor sale la componenta de modul maxim, rezultand sirul:
![]() . (4.29)
. (4.29)
Se poate scrie ca:
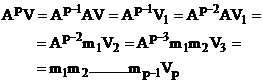 . (4.30)
. (4.30)
Tinand cont de (4.27) se poate scrie:
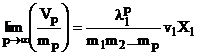 . (4.31)
. (4.31)
Rezulta ca
pentru p suficient de mare, vectorul ![]() este proportional
cu vectorul propriu X1 ce corespunde valorii proprii l
este proportional
cu vectorul propriu X1 ce corespunde valorii proprii l
![]() . (4.32)
. (4.32)
Se poate scrie ca:
![]() . (4.33)
. (4.33)
Valoarea proprie l se obtine impartind
componenta la componenta vectorii ![]() si
si ![]() , deci:
, deci:
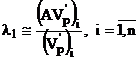 . (4.34)
. (4.34)
Daca relatia (4.31) se scrie si pentru (p-1) si se face impartirea membru cu membru, se poate scrie ca:
![]() . (4.35)
. (4.35)
Calculul se
opreste la acea valoare a lui p pentru care valorile obtinute pentru ![]() in doua
iteratii consecutive sunt suficient de apropiate, conform unei erori
impuse.
in doua
iteratii consecutive sunt suficient de apropiate, conform unei erori
impuse.
Metoda puterii directe poate fi utilizata pentru determinarea in continuare a celorlalte valori proprii, in ordine descrescatoare, daca se procedeaza astfel:
Avand
obtinuta valoarea proprie ![]() si vectorul
propriu corespunzator
si vectorul
propriu corespunzator ![]() , se noteaza cu
, se noteaza cu ![]() vectorul propriu
pentru
vectorul propriu
pentru ![]() corespunzator lui
corespunzator lui
![]() .
.
Avem:
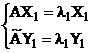 . (4.36)
. (4.36)
Se compune matricea:
![]() . (4.37)
. (4.37)
De remarcat in (4.37) ca ![]() este o matrice iar
este o matrice iar ![]() un scalar.
un scalar.
Fie Xj vectorul propriu ce corespunde valorii proprii lj a lui A. Tinand cont de asociativitatea produsului de matrice, vom avea:
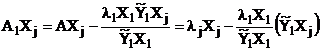 . (4.38)
. (4.38)
Dar ![]() daca
daca ![]() , iar ecuatia (4.38) devine:
, iar ecuatia (4.38) devine:
![]() . (4.39)
. (4.39)
Daca ![]() , atunci ecuatia (4.38) devine:
, atunci ecuatia (4.38) devine:
![]() . (4.40)
. (4.40)
Din (4.39) si
(4.40) rezulta ca matricea A1 are drept valori proprii
numerele ![]() si vectorii
proprii
si vectorii
proprii ![]()
Valoarea proprie
dominanta ![]() a disparut din
setul de valori proprii ale lui
a disparut din
setul de valori proprii ale lui ![]() . Cea mai mare valoare proprie, in modul, este acum
. Cea mai mare valoare proprie, in modul, este acum ![]() .
.
Aplicand metoda
puterii directe pentru matricea ![]() se determina
se determina ![]() . Se poate proceda la determinarea unei noi matrice
. Se poate proceda la determinarea unei noi matrice ![]() si a valorii
proprii
si a valorii
proprii ![]() , s.a.m.d. Determinarea vectorului propriu
, s.a.m.d. Determinarea vectorului propriu ![]() ce corespunde lui
ce corespunde lui ![]() pentru matricea
pentru matricea ![]() se poate face prin
determinarea solutiei sistemului omogen
se poate face prin
determinarea solutiei sistemului omogen
![]() (4.41)
(4.41)
prin metoda descrisa in Cap.
Metoda descrisa
pentru calculul celei mai mari valori proprii poate fi modificata astfel
incat sa poata fi determinata cea mai mica valoare proprie,
![]() . In acest caz, pornind de la un vector oarecare V, se
construieste un proces iterativ prin inmultire cu matricea A-1
obtinand metoda puterii inverse. Se stie ca matricea
inversa A-1 are aceiasi vectori proprii ca si A iar
valorile sale proprii sunt inversele valorilor proprii ale lui A.
. In acest caz, pornind de la un vector oarecare V, se
construieste un proces iterativ prin inmultire cu matricea A-1
obtinand metoda puterii inverse. Se stie ca matricea
inversa A-1 are aceiasi vectori proprii ca si A iar
valorile sale proprii sunt inversele valorilor proprii ale lui A.
Se considera vectorul V dat de relatia (4.21).
Prin inmultire la stanga cu A-1 se obtine:
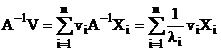 . (4.42)
. (4.42)
Din aproape in aproape obtinem:
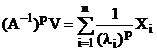 . (4.43)
. (4.43)
Considerand valoarea proprie ![]() cea mai mica in
modul, avem:
cea mai mica in
modul, avem:
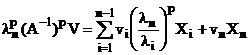 . (4.44)
. (4.44)
Trecand la limita se obtine:
![]() (4.45)
(4.45)
Daca in aceasta situatie sirul de vectori se noteaza:
![]() (4.46)
(4.46)
efectuand normarea vectorilor din cadrul fiecarui pas rezulta:
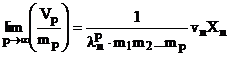 . (4.47)
. (4.47)
In aceasta
situatie, vectorul ![]() este proportional cu vectorul
este proportional cu vectorul ![]() , si se poate scrie:
, si se poate scrie:
![]() . (4.48)
. (4.48)
Rezulta ca:
![]() (4.49)
(4.49)
iar pentru ![]() se poate scrie
se poate scrie
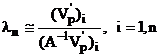 (4.50)
(4.50)
sau inca
![]() . (4.51)
. (4.51)
In utilizarea acestor doua metode este necesar sa se porneasca de la un vector arbitrar V. De obicei se alege un vector cat mai simplu, cel mai utilizat fiind vectorul avand toate componentele egale cu unitatea.
Aceste metode pot fi
modificate in continuare pentru obtinerea unor metode noi, numite 'cu
deplasarea originii'. Se poate arata ca matricele (A-qI) si
A au acelasi set de vectori proprii,
iar pentru fiecare valoare proprie ![]() a matricei A
corespunde valoarea proprie (
a matricei A
corespunde valoarea proprie (![]() - q) a matricei (A-qI).
- q) a matricei (A-qI).
Se pot constitui procese iterative bazate pe puterea directa sau inversa a matricei (A-qI).
O alegere
corecta a lui q poate face ca valoarea proprie (![]() - q) sa devina cea mai mica (sau cea mai
mare), de unde, prin folosirea metodei puterii inverse sau a puterii directe,
se poate determina valoarea proprie (
- q) sa devina cea mai mica (sau cea mai
mare), de unde, prin folosirea metodei puterii inverse sau a puterii directe,
se poate determina valoarea proprie (![]() - q).
- q).
In continuare, se pot modifica matricele in sensul determinarii celorlalte valori proprii, prin modificarea constantei q, pozitiva sau negativa.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2817
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved