| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
In sectiunea 1.6, am introdus notiunea de torsiune ca fiind un anumit factor in formulele lui Frenet. In cele ce urmeaza, vom da torsiunii o definitie geometrica, analoaga cu definitia curburii.
Fie M un punct al urmei al curbei parametrizate C, de clasa C3 si fie N I , N ¹ M. In cazul curbelor plane, binormalele in M si N sunt perpendiculare pe planul curbei. Cand curba nu este plana, unghiul al planelor osculatoare in punctele M si N, care coincide cu unghiul binormalelor in M si N, masoara deviatia pe care o sufera binormala cand punctul curent descrie arcul MN, datorita faptului ca arcul MN iese din planul osculator M. Fie | s| lungimea arcului MN.
Teorema 7.1. O curba parametrizata de clasa C3
are torsiunea absoluta |k2(s)| bine determinata in orice punct in care
curbura este nenula. Torsiunea absoluta este egala cu limita raportului ![]() cand N
→ M, N I Mai
precis, daca
cand N
→ M, N I Mai
precis, daca ![]() este
parametrizarea naturala a curbei, atunci
este
parametrizarea naturala a curbei, atunci
![]() (7.1)
(7.1)
Demonstratie. Din motive de continuitate, curbura fiind
nenula in punctul M(x(s),
y(s),
z(s)),
este nenula intr-o vecinatate a acestui punct. In orice punct in care curbura
este nenula, vectorii ![]() si
si ![]() sunt necoliniari, deci in orice punct din
vecinatatea lui M exista un plan
osculator bine determinat.
sunt necoliniari, deci in orice punct din
vecinatatea lui M exista un plan
osculator bine determinat.
Fie N(x(s
+ s), y(s + s), z(s + s)) si fie ![]() si
si ![]() versorii binormalelor in punctele M si N.
Unghiul dintre acesti versori fiind , din teorema
cosinusului rezulta ca
versorii binormalelor in punctele M si N.
Unghiul dintre acesti versori fiind , din teorema
cosinusului rezulta ca ![]() In
consecinta,
In
consecinta,
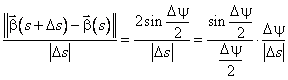
deci ![]() . Conform celei
de-a treia formule a lui Frenet, obtinem ca
. Conform celei
de-a treia formule a lui Frenet, obtinem ca ![]() , adica (7.1).
, adica (7.1).
In continuare, vom aborda problema calculului torsiunii. Din formula a doua a lui Frenet obtinem
![]()
Dar ![]() . Pe de
alta parte, din
. Pe de
alta parte, din ![]() rezulta
rezulta ![]() . Atunci
. Atunci
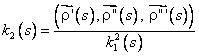 (7.2)
(7.2)
Asadar, torsiunea k2(s) a curbei C in punctul M este data de
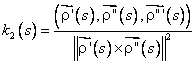 (7.3)
(7.3)
Ne propunem acum sa gasim formula de calcul a torsiunii in cazul unei parametrizari oarecare. Fie, deci, (I, r) un reprezentant al curbei C si (j, ) drumul parametrizat natural echivalent cu drumul (I, r). Din (4.26) rezulta
![]() (7.4)
(7.4)
Din (4.25), (4.26) si (7.4) obtinem
![]() .
.
Dar din (4.25) si (4.27) avem
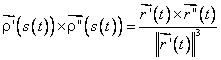
Atunci, din (7.3) rezulta
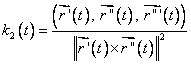
sau
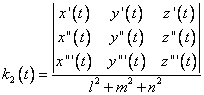 (7.5)
(7.5)
unde l, m, n sunt dati de (4.13).
Definitie. Se numeste raza de torsiune intr-un punct si se
noteaza cu T(t) inversa torsiunii in acel punct, adica ![]() .
.
Observatii.
1) Curbura si torsiunea unei curbe intr-un punct au fost definite geometric, deci exprima proprietati intrinseci ale curbei. Asadar, curbura si torsiunea sunt invarianti scalari ai curbei. Se poate arata ca daca se cunosc curbura si torsiunea unei curbe, curba este determinata abstractie facand de pozitia sa.
2) Curbele cu proprietatea T(t) d2 = const., unde d este distanta de la origine la planul osculator in punctul curent al curbei, au fost studiate de matematicianul roman Gh. Titeica. De aceea ii poarta numele, numindu-se curbe Titeica.
3) O curba este
plana daca si numai daca torsiunea ei in orice punct este nula. Intr-adevar,
curba fiind plana, in orice punct al curbei planul osculator coincide cu planul
curbei, deci ![]() Conform (7.1), k2(s) = 0. Reciproc,
din k2(s) = 0 rezulta ca
Conform (7.1), k2(s) = 0. Reciproc,
din k2(s) = 0 rezulta ca ![]() este un vector constant, deci
este un vector constant, deci ![]() Dar
Dar
![]() , adica
, adica ![]() sau A x'(s) + B
y'(s) +
sau A x'(s) + B
y'(s) +
C z'(s) = 0. Integrand,
rezulta A x(s) + B y(s) + C
z(s) = -D, deci curba se afla in planul de ecuatie Ax + by
+ Cz + D = 0.
Probleme rezolvate.
1) Sa se
calculeze torsiunea curbei de reprezentant ![]() , r(t) = (acost, asint,
bt), a, b > 0.
, r(t) = (acost, asint,
bt), a, b > 0.
Solutie. Imaginea curbei este elicea cilindrica.
Avem: ![]()
![]()
![]() . Atunci
. Atunci ![]() , deci
, deci ![]() . Folosind (7.5),
obtinem
. Folosind (7.5),
obtinem ![]() . Asadar,
torsiunea elicei este constanta.
. Asadar,
torsiunea elicei este constanta.
2) Sa se determine functia t → f(t), t
> 0, astfel incat curba de reprezentant ![]()
![]() sa fie o curba plana.
sa fie o curba plana.
Solutie. Conditia k2(t) = 0, t >0, conduce la ecuatia diferentiala ![]() . Rezulta ca
. Rezulta ca ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2562
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved