| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Variabile aleatoare. Caracteristici numerice. Functie de repartitie
Una dintre notiunile fundamentale ale teoriei probabilitatilor este aceea de variabila aleatoare.
Evenimentele unui camp de probabilitate nu sunt, principial, marimi in intelesul atribuit acestora in stiintele naturale sau tehnica; ele se descriu insa cu ajutorul unor marimi avand valori reale si care, in general, sunt rezultatul unor masuratori. Principalul merit al actualei sistematizari a calcului probabilitatilor consta in definirea variabilelor aleatoare, deci a marimilor pe care ni le prezinta experimentul direct, sau teoriile destinate sa-l interpreteze.
Daca intelegem prin variabila aleatoare o functie reala definita pe multimea evenimentelor elementare asociate experimentului considerat vom putea ilustra prin exemple tipice pentru teoria probabilitatilor cum se trece de la un eveniment la o variabila aleatoare si anume:
Exemplul 3.1. Sa consideram un experiment care
are ca rezultat evenimentul A. In locul evenimentul A putem considera variabila
aleatoare ![]() care ia valoarea 1 daca s-a realizat A si 0
daca s-a realizat
care ia valoarea 1 daca s-a realizat A si 0
daca s-a realizat ![]() . Am
definit o variabila aleatoare bernuolliana cu doua valori (variabila
indicatoare a evenimentului A) prin relatia:
. Am
definit o variabila aleatoare bernuolliana cu doua valori (variabila
indicatoare a evenimentului A) prin relatia:
![]()
In practica este de multe ori mai comod ca in locul evenimentelor sa utilizam variabilele aleatoare indicatoare care le sunt asociate.
Variabile aleatoare discrete
Fie ![]() un s-camp
de probabilitate si
un s-camp
de probabilitate si ![]() un sistem complet (finit sau numarabil) de
evenimente. Sistemul numeric
un sistem complet (finit sau numarabil) de
evenimente. Sistemul numeric ![]()
![]() , se
numeste distributia s-campului de probabilitate
, se
numeste distributia s-campului de probabilitate
Definitie. Numim variabila aleatoare
discreta o functie ![]() definita pe multimea evenimentelor elementare
definita pe multimea evenimentelor elementare ![]() cu valori reale daca:
cu valori reale daca:
![]() ia valorile
ia valorile ![]() ,
, ![]() ;
;
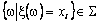 ,
, ![]() .
.
O variabila aleatoare discreta pentru care I este finita se numeste variabila aleatoare simpla.
Schematic variabila aleatoare ![]() se noteaza prin:
se noteaza prin:
|
|
Tabloul (3.1) se numeste distributia sau repartitia
variabilei aleatoare ![]() .
.
Numarul produselor defecte dintr-un lot examinat, numarul de defectiuni care apar intr-o anumita perioada de functionare a unui dispozitiv, indicatorul unui eveniment A sunt variabile aleatoare discrete.
Faptul ca ![]() ne sugereaza ideea ca aceasta suma se
repartizeaza intr-un anumit mod intre aceste valori
ne sugereaza ideea ca aceasta suma se
repartizeaza intr-un anumit mod intre aceste valori ![]() deci din punct de vedere probabilistic o
variabila aleatoare este complet determinata daca se da o astfel de repartitie.
Vom stabili o astfel de lege de repartitie.
deci din punct de vedere probabilistic o
variabila aleatoare este complet determinata daca se da o astfel de repartitie.
Vom stabili o astfel de lege de repartitie.
Una din formele cele mai simple in care putem reprezenta o astfel de lege este forma schematica (3.1) sau sub forma unui tabel.
|
xi |
x1 |
x2 |
xI |
xn |
||
|
pi |
p1 |
p2 |
pI |
pn |
iar o alta forma este cea grafica luand pe axa absciselor valorile xi iar pe axa ordonatelor probabilitatile corespunzatoare. Putem obtine unind aceste puncte poligonul de repartitie
|
|
sau diagrama in batoane
|
|
Exemplul
3.2. Un lot de piese este supus unui control de calitate in
modul urmator: se extrage pe rand cate o piesa care se cerceteaza daca poate fi
admisa sau nu. Se cerceteaza 5 piese. Daca piesa din extractia de rang ![]() nu corespunde, lotul se respinge. Sa se scrie
tabloul de repartitie al variabilei aleatoare care reprezinta
numarul de piese cercetate, daca probabilitatea ca o piesa luata la intamplare
din lot sa fie admisa este 0,85.
nu corespunde, lotul se respinge. Sa se scrie
tabloul de repartitie al variabilei aleatoare care reprezinta
numarul de piese cercetate, daca probabilitatea ca o piesa luata la intamplare
din lot sa fie admisa este 0,85.
Sa se traseze poligonul de repartitie corespunzator.
R. Variabila aleatoare ![]() poate lua valorile:
poate lua valorile:
1 - daca prima piesa e rebut, deci ![]()
2 - daca prima piesa extrasa e buna, iar a doua rebut: ![]() ;
;
3 - daca primele doua piese sunt bune si a treia
rebut; ![]()
4 - primele trei piese sunt bune, iar a patra rebut
: ![]()
5 - primele patru piese sunt bune; ![]()
Deci ![]()
Poligonul de repartitie este cel din figura:
|
|
Momentele unei variabile aleatoare discrete
Momentele unei variabile aleatoare discrete sunt valorile tipice cele mai frecvent utilizate in aplicatii.
Definitie. Fie ![]() o variabila aleatoare discreta care ia
valorile
o variabila aleatoare discreta care ia
valorile ![]() cu probabilitatile
cu probabilitatile ![]() ,
, ![]() . Daca
seria
. Daca
seria ![]() este absolut convergenta, expresia:
este absolut convergenta, expresia:
|
|
se numeste valoare medie a
variabilei aleatoare discrete ![]() .
.
Daca ξ este o variabila aleatoare simpla care ia valorile x1,.,xn cu probabilitatile p1,.,pn atunci valoarea medie va fi:
|
|
Vom da in continuare cateva proprietati ale valorilor medii:
(P1)
Daca si η sunt doua variabile aleatoare discrete definite prin (3.2.) si daca M ) si M exista, atunci exista valoarea medie ![]() M(x h) si avem:
M(x h) si avem:
|
|
Prin recurenta, se obtine:
(P2)
Fie ![]() , (
, (![]() ) n
variabile aleatoare discrete. Daca
) n
variabile aleatoare discrete. Daca ![]() (
(![]() ) exista,
atunci
) exista,
atunci ![]() exista si
exista si
|
|
(P3)
Fie ![]() o
variabila aleatoare discreta si c o
o
variabila aleatoare discreta si c o ![]() exista,
atunci
exista,
atunci ![]() exista
si avem
exista
si avem
|
|
(P4)
Fie ![]()
![]() ) n variabile discrete si
) n variabile discrete si ![]()
![]() ), n constante. Daca
), n constante. Daca ![]()
![]() ) exista, atunci
) exista, atunci ![]() exista si
exista si
|
|
(P5)
Valoarea medie a variabilei aleatoare ![]() este nula. (
este nula. (![]() se numeste
abaterea variabilei aleatoare
se numeste
abaterea variabilei aleatoare ![]() ).
).
(P6)
Inegalitatea lui Schwarz. Fie ![]() si
si ![]() doua
variabile aleatoare discrete pentru care exista
doua
variabile aleatoare discrete pentru care exista ![]() si
si ![]() . Avem:
. Avem:
|
|
(P7)
Daca ![]() si
si ![]() sunt
doua variabile aleatoare discrete independente si daca
sunt
doua variabile aleatoare discrete independente si daca ![]() si
si ![]() exista,
atunci
exista,
atunci ![]() exista
si
exista
si
|
|
Exemplul
3.3. Un aparat este format din 5 elemente care se pot defecta
independent unul de altul. Numerotam elementele de la 1 la 5 si fie ![]() probabilitatea sa se defecteze elementul cu
numarul k,
probabilitatea sa se defecteze elementul cu
numarul k, ![]() . Sa
se calculeze valoarea medie a numarului de defectiuni.
. Sa
se calculeze valoarea medie a numarului de defectiuni.
R. Fie ![]() variabila aleatoare asociata elementului cu
numarul k care ia valori pe 1 sau 0 dupa cum elementul se defecteaza sau nu:
variabila aleatoare asociata elementului cu
numarul k care ia valori pe 1 sau 0 dupa cum elementul se defecteaza sau nu:
![]()
![]()
Variabila aleatoare care da numarului de defectiuni este ![]() , deci:
, deci:
![]()
Avem:
![]()
![]() de unde:
de unde:
![]()
Definitie. Fie ![]() o variabila
aleatoarea discreta si r un numar natural. Daca exista valoarea medie a
variabilei aleatoare
o variabila
aleatoarea discreta si r un numar natural. Daca exista valoarea medie a
variabilei aleatoare ![]() , atunci aceasta valoare medie se numeste moment de ordin r al variabilei
aleatoare
, atunci aceasta valoare medie se numeste moment de ordin r al variabilei
aleatoare ![]() si se noteaza:
si se noteaza:
|
|
Valoarea medie a
variabilei aleatoare ![]() se numeste moment absolut de ordin r al variabilei
aleatoare
se numeste moment absolut de ordin r al variabilei
aleatoare ![]() si se noteaza:
si se noteaza:
|
|
Definitie. Data o variabila aleatoare discreta ![]() , momentul de ordinul r al variabilei aleatoare abatere a
lui
, momentul de ordinul r al variabilei aleatoare abatere a
lui ![]() se numeste moment centrat de ordinul r a lui
se numeste moment centrat de ordinul r a lui ![]() si se noteaza
si se noteaza
|
|
Momentul centrat de
ordinul doi a variabilei aleatoare discrete ![]() se numeste dispersie sau varianta si se noteaza prin
se numeste dispersie sau varianta si se noteaza prin ![]() sau
sau ![]() , deci:
, deci:
|
|
Numarul ![]() se numeste abatere medie patratica a lui
se numeste abatere medie patratica a lui ![]() .
.
Vom da in continuare cateva proprietati ale dispersiei si ale abaterii medii patratice:
(D1) Are loc egalitatea
|
|
(D2) Daca ![]() cu a si b constante,
atunci
cu a si b constante,
atunci ![]()
(D3) Fie ![]() , n variabile aleatoare discrete doua cate doua independente si
, n variabile aleatoare discrete doua cate doua independente si ![]() , n constante. Avem
, n constante. Avem
|
|
(D4)
Inegalitatea lui Cebisev Fie ![]() o variabila
aleatoare. Are loc inegalitatea:
o variabila
aleatoare. Are loc inegalitatea:
|
|
pentru
orice ![]()
Variabile aleatoare de tip continuu
Fie ![]() un -camp de probabilitate.
un -camp de probabilitate.
Definitie. Se numeste variabila
aleatoare o functie ![]() (definita pe
multimea evenimentelor elementare cu valori reale), astfel incat toate
multimile de forma
(definita pe
multimea evenimentelor elementare cu valori reale), astfel incat toate
multimile de forma ![]() apartin lui
apartin lui ![]() pentru orice
pentru orice ![]()
Vom da in continuare cateva proprietati ale variabilelor aleatoare:
(P1)
Fie ![]() o
variabila aleatoare si c o constanta; atunci
o
variabila aleatoare si c o constanta; atunci ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() cu
cu ![]() sunt
variabile aleatoare.
sunt
variabile aleatoare.
(P2)
Fie ![]() si
si ![]() doua
variabile aleatoare; atunci
doua
variabile aleatoare; atunci ![]() ,
, ![]() ,
, ![]() .
.
(P3)
Daca ![]() si
si ![]() sunt doua
variabile aleatoare atunci
sunt doua
variabile aleatoare atunci ![]() ,
, ![]() ,
, ![]() ,
, ![]() daca:
daca:
![]() ,
, ![]() ,
, ![]() sunt de
asemenea variabile aleatoare.
sunt de
asemenea variabile aleatoare.
Teorema 3.1. Daca ![]() este o variabila aleatoare nenegativa, exista
un sir crescator
este o variabila aleatoare nenegativa, exista
un sir crescator ![]() de variabile aleatoare simple, nenegative,
care converge catre
de variabile aleatoare simple, nenegative,
care converge catre ![]() .
.
Teorema 3.2. Daca ![]() este un sir de
variabile aleatoare atunci
este un sir de
variabile aleatoare atunci ![]()
![]()
![]()
![]() sunt de asemenea
variabile aleatoare.
sunt de asemenea
variabile aleatoare.
Definitie. Vom spune
ca variabilele aleatoare ![]() sunt independente daca pentru toate sistemele
reale
sunt independente daca pentru toate sistemele
reale ![]() avem:
avem:
![]()
Functie de repartitie
Definitie. Se numeste functie
de repartitie a variabilei aleatoare ![]() , functia:
, functia:
|
|
definita pentru orice ![]() .
.
Din aceasta definitie rezulta ca orice variabila aleatoare poate fi data prin intermediul functiei sale de repartitie.
Daca ![]() este o variabila aleatoare discreta cu
este o variabila aleatoare discreta cu ![]() ,
, ![]() atunci din (3.16.) rezulta:
atunci din (3.16.) rezulta:
|
|
si se numeste functie de repartitie de tip discret.
Rezulta ca in acest caz F este o functie in scara, adica ia valori constante pe
intervalele determinate de punctele ![]()
![]()
|
|
Fig. 3.1

Graficul ei este cel din fig. 3.1.
Teorema 3.3. Functia de repartitie a unei variabile aleatoare are urmatoarele proprietati:
![]() daca
daca ![]()
![]()
![]() pentru orice
pentru orice ![]()
![]()
![]()
Teorema 3.4. Orice
functie ![]() monotona,
nedescrescatoare, continua la stanga si cu
monotona,
nedescrescatoare, continua la stanga si cu ![]()
![]() este functia de
repartitie a unei variabile aleatoare definita pe un camp de probabilitate
convenabil ales.
este functia de
repartitie a unei variabile aleatoare definita pe un camp de probabilitate
convenabil ales.
Teorema 3.5. Fie ![]() o variabila aleatoare a carei functie de
repartitie este
o variabila aleatoare a carei functie de
repartitie este ![]() Fie a si b doua numere reale cu
Fie a si b doua numere reale cu ![]() . Au loc egalitatile:
. Au loc egalitatile:
![]()
![]()
![]()
![]()
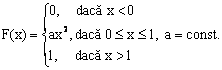
Se cere:
Sa se determine constanta a asa incat F sa fie functie de repartitie.
Sa se calculeze ![]()
R. Functia F este continua in toate punctele axei reale cu
exceptia punctului ![]() . Tinand seama de
definitia functiei de repartitie trebuie ca F sa fie continua la stanga in
orice punct
. Tinand seama de
definitia functiei de repartitie trebuie ca F sa fie continua la stanga in
orice punct ![]() si
si ![]() deci in
deci in ![]() trebuie sa avem:
trebuie sa avem:
![]()
de unde rezulta:
![]()
Daca cerem ca F sa
fie continua in ![]() atunci
atunci ![]() . Avem:
. Avem:
![]()
de unde
![]()
Definitie. Fie ![]() o variabila aleatoare a carei functie de repartitie este
o variabila aleatoare a carei functie de repartitie este ![]() . Daca exista o functie reala ƒ
definita si integrabila pe R asa incat:
. Daca exista o functie reala ƒ
definita si integrabila pe R asa incat:
|
|
atunci ![]() se numeste functie de repartitie absolut continua,
iar
se numeste functie de repartitie absolut continua,
iar ![]() se numeste variabila aleatoare absolut continua.
Functia ƒ(x) se numeste densitate
de probabilitate (repartitie),
iar expresia ƒ(x)dx se numeste lege de probabilitate elementara.
se numeste variabila aleatoare absolut continua.
Functia ƒ(x) se numeste densitate
de probabilitate (repartitie),
iar expresia ƒ(x)dx se numeste lege de probabilitate elementara.
Densitatea de probabilitate are urmatoarele proprietati:
![]() pentru
orice
pentru
orice ![]() .
.
![]()
Pentru orice ![]() reali are loc relatia:
reali are loc relatia:
P(a £ x < b) = ![]()
![]()
Se cere:
Sa se determine
Sa se determine functia de repartitie corespunzatoare.
Sa se calculeze ![]()
R. 1. Din proprietatile densitatii de probabilitate deducem:
![]()
de unde ![]()
2. Fie F functia de repartitie corespunzatoare. Avem:
![]()
Pentru ![]()
![]() , deci
, deci ![]()
Pentru ![]() , avem:
, avem:
![]()
Pentru ![]() , avem:
, avem:
![]()
Deci:
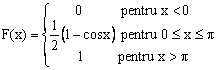
3. ![]() .
.
Graficul functiei ƒ este cel din fig. 3.2, iar al functiei F este cel din fig. 3.3.
Aria hasurata din fig. 3.2. reprezinta probabilitatea ceruta la punctul 3.
|
|
|
|
Fig. 3.2. |
Fig. 3.3. |
Momentele unei variabile de tip continuu
Fie ![]() un -camp de probabilitate si
un -camp de probabilitate si
![]() o variabila aleatoare a carei functie de
repartitie este
o variabila aleatoare a carei functie de
repartitie este ![]() . Fie
. Fie ![]() densitatea de repartitie a variabilei
aleatoare
densitatea de repartitie a variabilei
aleatoare ![]()
Definitie. Se numeste valoare medie a variabilei aleatoare ![]() expresia:
expresia:
|
|
Definitie. Se numeste moment
de ordinul r, ![]() , al variabilei aleatoare continue
, al variabilei aleatoare continue ![]() , expresia:
, expresia:
|
|
iar expresia:
|
|
se numeste moment
absolut de ordin r al variabilei aleatoare ![]()
In acelasi mod in care s-au definit momentul centrat de ordinul r, dispersia, abaterea medie patratica in cazul variabilelor aleatoare discrete, se definesc si pentru variabile aleatoare de tip continuu. Proprietatile valorii medii si ale dispersiei date pentru variabile aleatoare de tip discret se mentin pentru variabile aleatoare de tip continuu. In aplicatii se intalnesc si urmatoarele caracteristici:
Asimetria si excesul. Se numesc asimetrie, As, si exces, E, numerele:
|
|
daca momentele respective exista.
Exemplul 3.7. Fie ![]() o variabila aleatoare de tip continuu cu
densitatea de probabilitate:
o variabila aleatoare de tip continuu cu
densitatea de probabilitate:
![]()
![]()
Sa se calculeze valoarea medie, dispersia, coeficientul de asime-trie si excesul.
R. Avem:
![]()
![]()
Din cauza simetriei
repartitiei date rezulta ![]() .
.
![]()
deci E = 3.
Definitie Se numeste moment
centrat in a de ordinul r al variabilei aleatoare ![]() , momentul de ordinul r al variabilei aleatoare
, momentul de ordinul r al variabilei aleatoare ![]() , iar momentele
, iar momentele ![]() se numesc momente absolute centrate in a de ordinul r.
se numesc momente absolute centrate in a de ordinul r.
Din definitie rezulta urmatoarele proprietati:
(P1) Daca ![]() e o
variabila aleatoare cu
e o
variabila aleatoare cu ![]() si
si ![]() , are loc inegalitatea:
, are loc inegalitatea:
|
|
(P2)
Daca ![]() si
si ![]() sunt doua variabile aleatoare independente care au aceeasi functie de
repartitie F si
sunt doua variabile aleatoare independente care au aceeasi functie de
repartitie F si
![]() este un numar real oarecare, au loc inegalitatile:
este un numar real oarecare, au loc inegalitatile:
|
| |
|
|
pentru orice ![]() , cu
, cu ![]() mediana variabilei aleatoare
mediana variabilei aleatoare ![]() .
.
Din
definitia medianei rezulta ca in cazul unei variabile aleatoare ![]() de tip continuu, mediana este unic determinata
de egalitatea:
de tip continuu, mediana este unic determinata
de egalitatea:
![]()
Din punct de vedere
geometric, mediana este abscisa punctului prin care trece paralela la axa Oy,
care imparte in doua parti egale aria limitata de curba de ecuatie ![]() si axa Ox.
si axa Ox.
Exemplul 3.8. Fie ![]() o variabila aleatoare a carei densitate de
probabilitate este:
o variabila aleatoare a carei densitate de
probabilitate este:
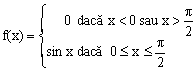
Sa se determine mediana lui ![]() .
.
|
|
|
Figura 3.4. |
R. Daca ![]() este de tip continuu, atunci:
este de tip continuu, atunci:![]() , de unde:
, de unde:
![]()
deci ![]() . Rezulta Me =
. Rezulta Me =
![]() (figura 3.4.).
(figura 3.4.).
Inegalitatea lui Markov. Fie ![]() o variabila aleatoare pozitiva a carei valoare
medie este finita. Pentru orice
o variabila aleatoare pozitiva a carei valoare
medie este finita. Pentru orice ![]() avem:
avem:
|
|
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2777
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved