| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
| електронен | изкуство култура | икономика | история | книга | компютри | медицина | психология |
| различни | социология | техника | управление | финанси | химия |
DOCUMENTE SIMILARE |
|
![]() (1)
(1)
Наличието в
електрическото
поле на
свободни
разпределени
в обема
заряди би
довело до
възникване
на електрически
ток. Поради
това
предположението,
че ![]() води
до
заключението
води
до
заключението
![]() по
повърхността
на
заредените
тела.
по
повърхността
на
заредените
тела.
От пълната система уравнения на електромагнитното поле остават следните уравнения, описващи изследваното електрическо поле:
![]()
![]()
![]()
![]() от
точката А
например до
точката Р, чиито
потенциал е
нула.
от
точката А
например до
точката Р, чиито
потенциал е
нула.
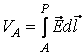
Линейният
интеграл от
вектора ![]() по
даден път от
точката А до
точката В е разликата
в
потенциалите
на точките А
и В
по
даден път от
точката А до
точката В е разликата
в
потенциалите
на точките А
и В
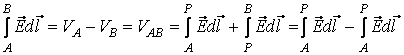
![]() (7)
(7)
![]() в
диференциалния
запис на
теоремата на
Гаус
в
диференциалния
запис на
теоремата на
Гаус
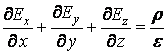 (8)
(8)
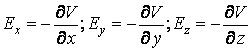
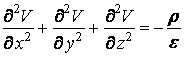
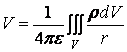
Ако в разглежданата област на пространството отсъствуват обемни електрически заряди, то уравнението на Поасон приема вида
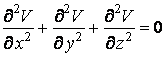
Уравнението (19) се нарича уравнение на Лаплас. Електростатичното поле удовлетворява уравнението на Лаплас.
V MKE
FEMM
Elecnet Infolytica corp
F Finite Element Method Magnetics MKE http femm berlios de
F D MKE
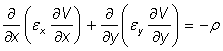 (13)
(13)
![]() -
електрическите
проницаемости
на средата по
направления
х и у;
-
електрическите
проницаемости
на средата по
направления
х и у;
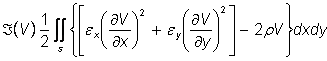 (14)
(14)
Z
r mm mm V e V Електродите са разположени на височина 50 см от повърхноста на земята и следователно нейното влияние може да се пренебрегне, тъй като при разстояния около десет пъти по-големи от размера на телата електрическото поле затихва и потенциала му е нула.
Y
File New
Create new problem lectrostatic
O File Save as Spheres
Problem От “Problem type” се избира, а от “Units” –“milimeters”.
Problem
Problem type Planar
Frequency Hz електростатична задача).
Depth a
Length Units ilimeters
Solver Precision e
Min angle
Comment (коментар) – например, записва се Electric field of two high voltage spheres.
![]() на 0.1,
което
означава, че
разстоянието
между две
съседни
точки от
мрежата ще
бъде 0.1 mm snap to grid
на 0.1,
което
означава, че
разстоянието
между две
съседни
точки от
мрежата ще
бъде 0.1 mm snap to grid ![]() от
вертикалната
лента с
инструментите.
Snap to grid
от
вертикалната
лента с
инструментите.
Snap to grid
Point ![]()
Arc Segment ![]() Angle Max Segment Degrees
Angle Max Segment Degrees
OY OY Max Segment Degrees
Window Zoom най-долната точка, а след това до най-горната по ординатната ос точка. За Max Segment Degrees градуса.
View Natural
Properties Materials Property Definition Add Materials Block Property Name New Material Air ![]() и
и ![]() със
стойности
единица.
Щраква се върху
ОК и
се излиза от
прозореца. С
това е
дефиниран
нов материал
- въздух.
със
стойности
единица.
Щраква се върху
ОК и
се излиза от
прозореца. С
това е
дефиниран
нов материал
- въздух.
Block Labels ![]() от
лентата с
инструментите
и се позиционира
по един
блоков
етикет
(зелена
точка) за всяка
област с
различен
материал.
Както и
възловите
точки,
блоковите
етикети
могат да
бъдат
позиционирани
или с
щракване с левия
бутон на
мишката или с
диалоговата
кутия,
отваряща се
при
натискане на
клавиш <ТАВ>.
от
лентата с
инструментите
и се позиционира
по един
блоков
етикет
(зелена
точка) за всяка
област с
различен
материал.
Както и
възловите
точки,
блоковите
етикети
могат да
бъдат
позиционирани
или с
щракване с левия
бутон на
мишката или с
диалоговата
кутия,
отваряща се
при
натискане на
клавиш <ТАВ>.
Space Block Type Air Let Triange choose Mesh Size Triangle Side Length mm Triangle Side Length
да се дискретизира тази част от областта на крайни елементи т.е. проводящите сфери не са част от модела. Поради това след като се поставят зелените блокови етикети за материалите вътре във всяка от сферите от падащото меню се задава Block Type („тип на блока') да бъде <No mesh>.
mm
Air mm
Conductor Properties Conductors Add Property Circuit properties New Conductor High voltage Prescribed Voltage OK
V Zero Prescribed Voltage
V V Arc Segment ![]()
Space Arc segment properties In conductor High voltage Zero
потенциала V
Properties Boundry Add Property
Bondary property New Boundry Per BC Type Boundry Condition Type Periodic Ok Per Per
Arc Segment Arc Segment Properties None Per Per
![]() от
лентата с
инструментите.
Това
действие
генерира
мрежа с триъгълни
крайни
елементи за
задачата.
Ако
гъстотата на
мрежата не
съответствува
на желаната,
тя може да се
промени с
избиране
блоковите
етикети на
обектите и с
подходяща
промяна на
размера на
елементите,
дефиниран в
свойствата
на всеки обект.
В случая се
генерира
мрежа с 33775
възли и 66118
крайни елементи.
от
лентата с
инструментите.
Това
действие
генерира
мрежа с триъгълни
крайни
елементи за
задачата.
Ако
гъстотата на
мрежата не
съответствува
на желаната,
тя може да се
промени с
избиране
блоковите
етикети на
обектите и с
подходяща
промяна на
размера на
елементите,
дефиниран в
свойствата
на всеки обект.
В случая се
генерира
мрежа с 33775
възли и 66118
крайни елементи.
![]()
FEMMVIEW ![]()
FEMMVIEW
![]() се
изобразява
картина с
линиите на
електрическия
потенциал. Когато
се появи
диалоговата
кутия, се
избира Show equipotential lines и се
приемат
предложените
по подразбиране
стойности за
горна и долна
граница на
потенциала.
След това се
щраква върху ОК.
се
изобразява
картина с
линиите на
електрическия
потенциал. Когато
се появи
диалоговата
кутия, се
избира Show equipotential lines и се
приемат
предложените
по подразбиране
стойности за
горна и долна
граница на
потенциала.
След това се
щраква върху ОК.
![]() и
избиране на
опциите Show Density plot , Show legend
и
избиране на
опциите Show Density plot , Show legend
Grayscale
|
|
|
|
|
|
![]() може да
бъде
получено разпределението
на
интензитета
на електрическото
поле E Plotted Field Intensity E
може да
бъде
получено разпределението
на
интензитета
на електрическото
поле E Plotted Field Intensity E
интензитета на електрическото поле същата задача се решава с програмния пакет ЕlecNet
OY Това става автоматизирано от пакета FEMM .
|
|
|
|
|
|
Y
за да се изчертае линията по която ще се даде разпределението на интензитета. След това се щраква последователно върху точка от повърхноста на горната и долната сфера. Избира се от лентата с менютата Plot XY E Magnitude of field intensity
f y Elecnet a Electric field FORTRAN
O за сравнение максималните стойности на интензитета на електрическото поле.
|
FEMM |
Elecnet | ||
|
V m | |||
FEMM ![]() и след
това се
кликва с
левия бутон на
мишката в
областта на
решението ,
която се
маркирва и
става също
зелена на
цвят. След това
се натиска
бутона с
интеграла
и след
това се
кликва с
левия бутон на
мишката в
областта на
решението ,
която се
маркирва и
става също
зелена на
цвят. След това
се натиска
бутона с
интеграла ![]() и от
падащото
меню на
появилия се
прозорец се
избира Stored energy Ok
и от
падащото
меню на
появилия се
прозорец се
избира Stored energy Ok
![]()
U
FEMM Elecnet
|
FEMM |
Elecnet | ||
|
Съхранена енергия *10-4, J | |||
|
Капацитет*10-12, F |
За изчислението на началните напрежения в газ, в частност във въздуха, се използва условието за самостоятелност на разреждането във вида:
![]()
Ефективният коефициент на йонизация
За въздуха тази функция добре се апроксимира чрез формулата
![]()
Физическия смисъл на условието ( ) се състои в това, че по дължината на промеждутъка или в зоната, където Е>Екр трябва да се произведат определен брой ефективни йонизации, за да се получи самостоятелно разреждане.
За въздуха добро съвпадение на изчислителните и опитни значения на началните напрежения се осигурява при К=8.2
В най-обикновения случай на еднородно поле напрежението, следователно и
![]()
S
За въздуха от (
![]()
![]() се мени
по
продължение
на силовата линия
на полето.
Затова е
необходимо
да се направи
интегриране
по
продължение
на силовата
линия на
полето в
съответствие
с (
се мени
по
продължение
на силовата линия
на полето.
Затова е
необходимо
да се направи
интегриране
по
продължение
на силовата
линия на
полето в
съответствие
с (
При изчислението на началните напрежения се различават два характерни случая. В първия случай полето в промеждутъка е такова, че напрежението надхвърля критическото Е>Екр във всички точки на централната силова линия. Интегрирането в (
Вторият
случай се
характеризира
с това, че съотношението
![]() се
прилага само
върху част от
централната
силова линия.
Следователно
ефективната
йонизация също
така може да
се образува
само в
определена
част на
въздушния
промеждутък.
Така във втория
случай
интегрирането
в (4.1) не по
цялата
дължина на
силовата
линия, а само
в участъка,
където се
изпълнява
условието
се
прилага само
върху част от
централната
силова линия.
Следователно
ефективната
йонизация също
така може да
се образува
само в
определена
част на
въздушния
промеждутък.
Така във втория
случай
интегрирането
в (4.1) не по
цялата
дължина на
силовата
линия, а само
в участъка,
където се
изпълнява
условието ![]()
Началното напрежение изчислено по (
Формулите (
Изчисление на началното напрежение. Нека централната силова линия се явява права. Разстоянието от електрода до точката на силовата линия, в която се изпълнява условието Е=Екр ще обозначим с хкр.
В промеждутъка с известна конфигурация на полето разпределението на напрежението по продължение на централната силова линия се явява функция на различията на потенциалите между електродите “U x
![]()
![]()
U
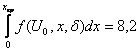
Но (4.4) относно U U U
Решението
на функцията ![]() е
възможно, ако
е известно
разпространението
на
напрежението
на полето по
централната
силова линия,
Така
изчислението
на
промеждутъка
на силовото
поле се явява
необходим
етап от
изчислението
на началното
напрежение.
е
възможно, ако
е известно
разпространението
на
напрежението
на полето по
централната
силова линия,
Така
изчислението
на
промеждутъка
на силовото
поле се явява
необходим
етап от
изчислението
на началното
напрежение.
q
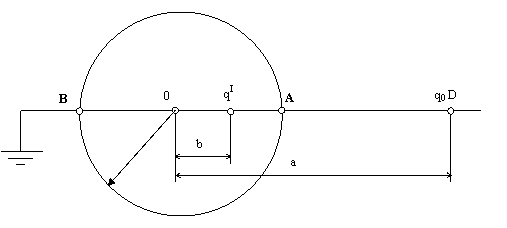

e q q q DO q DO q
Ще съставим уравнения относно потенциала произволни две точки на повърхността на сферата. Най-лесно е това да се направи за точките А и В. За разположението на зарядите дадени на фигура

q b
![]()
![]()
Тъй
като
потенциала
от зарядите q q ![]() q q q
q q q
![]() U
U ![]() r r r S
r r r S
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

За
разположим в
центъра на
сферата I ![]() q I U II
q I U II ![]() II q II q II
II q II q II ![]()
![]()
![]() осигуряват
осигуряват
![]()
![]() намаля
еквипотенциалноста
на повърхността
на сфера I
намаля
еквипотенциалноста
на повърхността
на сфера I ![]() в сфера I.
Прехвърлянето
на заряда
в сфера I.
Прехвърлянето
на заряда ![]() в сфера I q
в сфера I q
След
всяко
прехвърляне
се осигурява
условие на
еквипотенциалност,
на
повърхността
на една от
сферите.
Еквипотенциалноста
на повърхността
на другата
сфера се
нарушава. За
да се
осигурят
условията ![]() U
U ![]() на
повърхностите
на двете
сфери е
необходимо
да се построи
безкрайна
система от заряди
–
прехвърляния.
Съгласно 4.5
значението и
положението
на зарядите в
процеса на
последователните
прехвърляния
се определят
като:
на
повърхностите
на двете
сфери е
необходимо
да се построи
безкрайна
система от заряди
–
прехвърляния.
Съгласно 4.5
значението и
положението
на зарядите в
процеса на
последователните
прехвърляния
се определят
като:
![]()
![]()
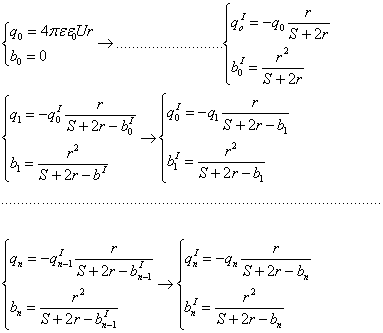
При
![]()
![]()
![]()
![]()
![]()
I q II
Определяйки положенията и значенията на последователните заряди – изображения е лесно да се изчисли напрежението във всяка точка на полето. Тя ще е равна на геометричната сума от вектори на напреженията, създадени от всеки заряд. Най-лесно се изчисляват напреженията на централната силова линия, която в нашия случай съвпада с линията, преминаваща през центровете на кълбата, или векторите на напреженията по тази линия съвпадат с посоката, затова геометричния сбор може да се замени с алгебричен. За всяка точка на централната силова линия напрежението се изразява така:
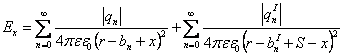
x I
От кадето последното уравнение може да се преобразува във вида:
4.7а 
![]()
От
където
следва че ![]()
![]()
![]()
![]() са
пропорционални
на
напрежението
между
сферите. Капацитетът
на
кълбовидния
разрядник се
определя като:
са
пропорционални
на
напрежението
между
сферите. Капацитетът
на
кълбовидния
разрядник се
определя като:

За изчислението на началното напрежение е нужно да се изчисли интеграла в израза (
U E x U ![]() по
същата линия.
(
по
същата линия.
(
В
зависимост
от
напрежението
приложено към
сферите,
минималното
значение на
напрежението
в
промеждутъка
може да бъде
повече или
по-малко от ![]()
![]() S
S ![]() йонизацията
е възможна в
двете зони,
прилягащи
към сферите.
йонизацията
е възможна в
двете зони,
прилягащи
към сферите.
В разглеждания от нас случай на заземяване на едното от кълбата разпределянето на напрежението по централната силова линия е несиметрично. Напрежението е повече в зоната, прилягаща към сферата намираща се под потенциала.
От
фиг. ![]() значенията
на интеграла
значенията
на интеграла ![]()
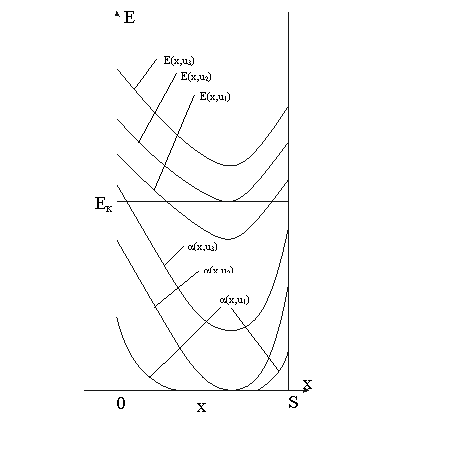

U U
S ![]()
Относителната грешка от 11,28
Изчислението
на началното
напрежение,
т.е. решението
на уравнението
( ![]() във
всяка точка
на
централната
силова линия.
Това
означава, че
интегрирането
върви само по
интегралите,
където се
изпълнява
това условие.
във
всяка точка
на
централната
силова линия.
Това
означава, че
интегрирането
върви само по
интегралите,
където се
изпълнява
това условие.
В Глава втора МКЕ се използува за решаване на задачата за анализа на
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2700
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved