CATEGORII DOCUMENTE
Afaceri Calculatoare Casa masina Didactica pedagogie Diverse Educatie Finante Geografie Istorie & politica Legislatie Limba Management Sanatate Tehnologie

Bulgara	Ceha slovaca	Croata	Engleza	Estona	Finlandeza	Franceza
Germana	Italiana	Letona	Lituaniana	Maghiara	Olandeza	Poloneza
Sarba	Slovena	Spaniola	Suedeza	Turca	Ucraineana

įstatymai	įvairių	Apskaitos	Architektūra	Biografija	Biologija	Botanika	Chemija
Ekologija	Ekonomika	Elektra	Finansai	Fizinis	Geografija	Istorija	Karjeros
Kompiuteriai	Kultūra	Literatūra	Matematika	Medicina	Politika	Prekyba	Psichologija
Receptus	Sociologija	Technika	Teisė	Turizmas	Valdymas	vietimas

Regresijos modeliai - Regresijos modelio samprata

ekonomika

+ Font mai mare | - Font mai mic


DOCUMENTE SIMILARE

Regresijos modeliai

1. Regresijos modelio samprata

Ekonomikos tyrimuose da˛nai tenka nustatyti dviejų dyd˛ių – Y, vadinamo iėjimo kintamuoju (pasekme), ir X, vadinamo įėjimo kintamuoju (prie˛astimi), – tarpusavio ryį. Pasaulyje esama nepaprastos įvairovės ių ryių tipų, bet visus juos galima suskirstyti į dvi grupes:

funkcinius;

koreliacijos.

Kiekvieną funkcinio ryio įėjimo kintamojo reikmę atitinka grie˛tai apibrė˛ta, fiksuota iėjimo kintamojo reikmė. ˇinant įmonės pajamas ir ilaidas, visuomet galima apskaičiuoti pelną. Funkcinė priklausomybė u˛raoma taip: Y=F(X).

Koreliacijos ryio įėjimo kintamojo kitimas veikia tik iėjimo kintamojo vidutines reikmes. Kai yra is ryys, esant tai pačiai įėjimo kintamojo reikmei, iėjimo kintamojo reikmės gali būti skirtingos. Taip yra todėl, kad iėjimo kintamojo dydį, be įėjimo kintamojo, sąlygoja daugybė kitų veiksnių, kurių įtakos negalima ivengti (kartais jie gali būti ne˛inomi). Tad koreliacijos ryys rykėja tik per statistinius stebėjimus: formaliai jis u˛raomas lygtimi: , kur e – atsitiktinė dedamoji, įvertinanti ir X, ir Y atsitiktinį pobūdį. Jei e=0, tai X ir Y sieja funkcinis ryys, o jei funkcija F(X) yra pastovi, tai X ir Y nepriklausomi. Kai yra koreliacijos ryys, funkcija Y=F(X) vadinama regresijos lygtimi (modeliu), o jos koeficientai – regresijos koeficientais.

Priklausomai nuo įėjimo kintamojo X matikumo, skiriami vienmačiai regresijos modeliai, kai kintamųjų skaičius lygus vienam, ir daugiamačiai, kai kintamųjų skaičiaus yra daugiau nei vienetas.

Regresinės lygties kintamųjų ryio stiprumą nusako ryio glaudumo rodikliai:

koreliacijos koeficientas r;

koreliacijos santykis R;

determinacijos koeficientas D.

Kai y ir x sieja tiesinis ryys, io ryio stiprumą nusako koreliacijos koeficientas, kuris nustatomas i stebėjimo duomenų (x_i, y_i), pagal ią formulę:

(1)

čia:	– įėjimo kintamojo reikmių vidurkis;
	– iėjimo kintamojo reikmių vidurkis;
	;
	– įėjimo kintamojo dispersija;
	– iėjimo kintamojo dispersija.

io koreliacijos koeficiento kitimo ribos . Jei r>0, regresijos funkcija didėja, o tai reikia, kad, didėjant x, didėja ir y. Kai r<0, x didėjant, y ma˛ėja. Kai , visi takai sutampa su tiesės linija.

Jei koreliacijos koeficientas r=0 arba artimas jam, tai dar nereikia, kad kintamieji x ir y yra nepriklausomi ar menkai priklausomi: jie gali būti susieti ne tiesine, o priklausomybe.

Jei tarp y ir x yra netiesinė koreliacija, ryio stiprumą nusako koreliacijos santykis:

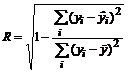; (2)

čia – iėjimo kintamojo reikmė, apskaičiuota pagal regresijos lygtį.

Akivaizdu, kad is koeficientas įgyja reikmes i intervalo . Kuo koeficiento reikmė artimesnė vienetui, tuo ryys stipresnis. Kuo regresijos lygtis geriau aprays stebėjimo duomenis, tuo skaitiklio narys bus ma˛esnis ir koeficientas didesnis.

Ir tiesinės, ir netiesinės koreliacijos atveju apskaičiuojamas determinacijos koeficientas:

. (3)

Jis rodo, kokią viso iėjimo kintamojo kitimo dalį nulemia įėjimo kintamojo kitimas, o (100-D) – likę neįvertinti veiksniai.

Regresiniuose modeliuose gali būti skaičiuojamos trys dispersijos:

liekamosios paklaidos

regresinės lygties

įvertinimo .

Liekamosios paklaidos dispersija parodo, kiek nukrypsta faktiki stebėjimo duomenys nuo apskaičiuotųjų pagal regresijos lygtį:

. (4)

Kuo ios dispersijos reikmė didesnė, tuo modelyje yra daugiau veikiančių y neįvertintų veiksnių.

Regresijos lygties dispersija, parodo nukrypimą nuo vidurkio:

. (5)

Ir įvertinimo dispersija įvertina suminį dispersijų poveikį:

. (6)

Kadangi ryio glaudumo rodikliai įvertinami pagal statistinius duomenis, visuomet būtina patikrinti ių rodiklių reikmingumą.

Koreliacijos koeficiento reikmingumas tikrinamas naudojant Stjudento kriterijų. Laikoma, kad koeficientas yra reikminis, jei galioja i nelygybė:

.; (7)

čia – Stjudento kriterijaus (t) lentelinė reikmė, esant nurodytajam patikimumui a ir n-m-1 laisvės laipsniams; m – regresijos lygtyje įvertinamų koeficientų skaičius.

Lentelinė Stjudento kriterijaus reikmė, kai patikimumas 0,05 ir laisvės laipsnis k=n-m-1, pateikta 1 lentelėje.

1 lentelė

Stjudento kriterijaus reikmė

k
t
k
t
k
t

Koreliacijos koeficiento vidutinis kvadratinis nukrypimas, esant didelei stebėjimo duomenų aibei (n>25), nustatomas taip:

. (8)

Esant ma˛ai aibei:

. (9)

Koreliacijos santykio reikmingumas tikrinamas pagal Fierio kriterijų:

; (10)

čia – Fierio kriterijaus (F) lentelinė reikmė, kai nurodytas patikimumas ir yra du laisvės laipsniai: k₁=(m-1) ir k₂=(n-m).

Vienmačių regresijos modelių sudarymas

Regresijos modelių koeficientų įvertinimas paremtas ma˛iausių kvadratų metodu:

. (11)

ios liekamosios paklaidos dispersijos minimizavimas leid˛ia geriausiai parinkti ne˛inomuosius regresijos lygties koeficientus.

Kiekvienas sudaromas regresijos modelis apima tris etapus:

ryio formos parinkimą;

kiekybinį regresijos lygties koeficientų įvertinimą;

ryio glaudumo reikmingumo nustatymą.

Parenkant modelio tipą, pirmiausia reikėtų grafikai pavaizduoti visus turimus stebėjimo duomenis ir nustatyti jų pasiskirstymą. Kuo glaud˛iau takai isidėstę, tuo stipresnis x ir y ryys. Kai takai isidėsto apskritime, galima teigti, kad koreliacijos ryio nėra. Atliekant grafinę koreliacijos lauko, t.y. statistinių duomenų, analizę, atskiri takai nejungiami kreive, tik pa˛ymima jų vieta.

Regresijos lygties koeficientai nustatomi, naudojant normalinių lygčių sistemą. Kadangi koeficientų skaičius kintamas, kiekvienam modelio tipui i sistema yra skirtinga.

Vienmačio regresijos modelio sudarymo struktūrinė schema pateikta 1 paveiksle. ioje schemoje rodomi trys galimi regresijos modelio sudarymo keliai.

1 pav. Vienmačio regresijos modelio sudarymo struktūrinė schema

Pasirinkus tiesinį regresijos modelį, galima i karto skaičiuoti regresijos lygties koeficientus ir pagal Fierio kriterijų patikrinti, ar gautoji lygtis reikminė. Jei i lygtis reikminė, apskaičiuojamas determinacijos koeficientas ir liekamosios paklaidos dispersija. Toks modelio sudarymo būdas tinka, kai i tikrųjų ˛inoma, kad yra tiesinis regresijos ryys. is kelias parodytas struktūrinėje schemoje punktyrais.

Dalinis tiesinio modelio būdas leid˛ia anksčiau nustatyti tiesinio ryio buvimą. Kai koreliacijos koeficientas nereikminis, būtina nagrinėti kreivinės regresijos modelio tipus.

Kreivinio modelio reikmingumas tikrinamas pagal Fierio kriterijų. Kartais gali būti sprend˛iamas geriausio kreivinio modelio parinkimo u˛davinys. Visi reikminiai kreiviniai modeliai palyginami pagal liekamosios paklaidos dispersijos reikmes. Atrenkamas tas modelis, kurio ma˛iausias.

3. Vienmatis tiesinės regresijos modelis

Tiesinės regresijos modeliai da˛niausiai naudojami, apraant ekonominius procesus. Klasikinis pavyzdys yra paklausos kreivė. Didėjant prekės kainai, pardavimų apimtys ma˛ėja.

Tiesinės regresijos modelio iraika:

; (12)

čia b – tiesinės regresijos lygties polinkis; a – tiesinės regresijos lygties kirtimas.

ioje lygtyje koeficientas gali įgyti bet kurias skaitines reikmes. ios lygties grafikai pavaizduoti 2 paveiksle.

2 pav. Tiesinės regresijos modelio grafikai

Paveikslo grafikai vaizduoja bet kurias galimas x reikmes. Ekonominiai kintamieji da˛niausiai įgyja tik teigiamas reikmes, tad ekonominėje analizėje tikslinga nagrinėti tik virutinį deinį kvadratą.

Bet kokią tiesę apibūdina du dyd˛iai, polinkis b, kuris rodo, kaip pakinta y, pakitus x, ir kirtimas a, t.y. y reikmė, kai x=0.

Bet kokios tiesės polinkis, t.y. santykis y pokyčio su x pokyčiu:

. (13)

is regresijos lygties koeficientas rodo, kiek y pasikeis, x pakitus vienu vienetu. Paprastai is polinkis priklauso nuo x ir y matavimo vienetų. Tarkime, kad paklausos kreivė, kai kaina matuojama centais, yra . ios kreivės polinkis b= Tai pačiai prekei kainą nustatant litais, paklausos kreivė bus y=2 - 0,02x ir b=0,0 Nors nagrinėjamas ekonominis reikinys yra tas pats, polinkis bus ne tas pats. ią „matavimo” problemą galima apeiti, regresijos lygtį sudarant standartizuotiems kintamiesiems.

ˇvaig˛dute pa˛ymėtiems standartizuotiems dyd˛iams būdinga tai, kad jų vidurkis lygus 0, o jų dispersijos lygios vienetui.

Kai b kinta, o a lieka pastovus, lygties grafikas sukasi apie kirtimą. Tai grafikai pavaizduota 3 paveiksle. Didėjant polinkiui, kreivė tampa nuo˛ulnesnė.

3 pav. Polinkio kitimo grafikai

Paklausos kreivės atveju kitimas – tai maksimali prekės kaina, u˛ kurią nebus parduota nė viena prekė. Kintant regresijos lygties kirtimui, o polinkiui nekintant, grafikas pakyla ar nusileid˛ia lygiagrečiai kitiems grafikams (˛r. 4 pav.).

Tiesinės regresijos lygtyje yra du ne˛inomi koeficientai - a ir b; jie nustatomi i normalinių lygčių sistemos:

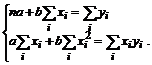(15)

Isprendę ią lygčių sistemą gauname:

; (16)

. (17)

4 pav. Kirtimo kitimo grafikai

Norint patikrinti lygties reikmingumą, pakanka patikrinti koeficiento b reikmingumą, naudojant Stjudento kriterijų:

; (18)

čia .

Ir tiesinės, ir kreivinės regresijos lygties atveju reikmingumas gali būti patikrintas naudojant ir Fierio kriterijų:

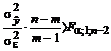. (19)

Pateiksime tiesinės regresijos modelio sudarymą konkrečiam u˛daviniui.

U˛davinys. Duomenys apie gaminio serijos dydį ir įpakavimo ilaidas pateikti 2 lentelėje. Sudaryti regresijos modelį.

2 lentelė

Gaminio įpakavimo ilaidų duomenys

	Gaminio mato vnt.	Gaminio įpakavimo ilaidų duomenys
Serijos dydis	tūkst.vnt.	x_i
Vieneto įpakavimo ilaidos	ct	y_i

Sprendimas. ių duomenų grafinis isidėstymas pateiktas 5 paveiksle.

5 pav. Koreliacijos laukas

I statistinių duomenų isidėstymo darome prielaidą, kad yra tiesinis koreliacijos ryys.

Įvertiname statistines charakteristikas:

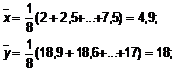
Tuomet koreliacijos koeficientas bus:

Tai rodo, kad koreliacijos ryys yra atvirktinis, t.y. didėjant serijos dyd˛iui, įpakavimo ilaidos ma˛ėja.

Patikriname koreliacijos koeficiento reikmingumą:

=2,57

Tad koreliacijos koeficientas yra reikminis.

Apskaičiuojame regresijos lygties koeficientus:

Tad regresijos lygties iraika yra

Koeficientas b rodo, kad, padidinus serijos dydį vienu tūkstančiu vienetų, produkcijos vieneto įpakavimo ilaidos suma˛ės dyd˛iu 0,34 cento.

Patikriname koreliacijos koeficiento b reikmingumą:

Tad koeficientas b yra reikminis, o kartu ir visa apskaičiuota tiesinės regresijos lygtis yra reikminė.

Determinacijos koeficientas

Tai rodo, kad tūkstančio vienetų įpakavimo ilaidos 82,8% priklauso nuo serijos dyd˛io, o 17,2% - nuo kitų neįvertintų reikmių.

4. Vienmatis hiperbolinės regresijos modelis

Kaip atskiras kreivinės vienmatės regresijos lygties atvejis aptartinas hiperbolinės regresijos modelis. is koreliacijos ryys pasi˛ymi tuo, kad, tolygiai x didėjant, y ma˛ėja greitėjančiai. Tipinis pavyzdys yra vidutinių gaminio ilaidų priklausomybė nuo pardavimo apimties.

Da˛niausia hiperbolinės regresijos modelio iraika:

. (20)

Hiperbolinės lygties parametrai a ir b nustatomi pagal normalinių lygčių sistemą:

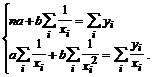(21)

U˛davinys. 3 lentelėje pateikti statistiniai duomenys. Sudaryti regresinį modelį.

3 lentelė

Gaminio vieneto ilaidų statistiniai duomenys

Pavadinimas	Mato vnt.	ˇymėjimas
Pardavimo apimtis	vnt.	x_i
Vieneto ilaidos	Lt	y_i
Apskaičiuotos vieneto ilaidos	vnt.

Sprendimas. Nubrai˛ome koreliacijos lauką (jis pateiktas 6 paveiksle). I statistikos duomenų idėstymo darome prielaidą, kad yra hiperbolinis koreliacijos ryys.

Įvertiname statistikos charakteristikas:

;

6 pav. Koreliacijos laukas

;

Nustatome regresijos lygties koeficientus:

Tada a=24,14; b=26,8.

Hiperbolinė regresijos lygtis u˛raoma taip:

ˇinant pardavimų apimtis, galima apskaičiuoti reikmes pagal pasirinktą regresijos modelį. Kai x=1, tada .

Kitos reikmės pateiktos 3 lentelėje.

Koreliacijos santykis nustatomas taip:

Visos regresijos lygties reikmingumas patikrinamas pagal Fierio kriterijų:

;

Kadangi 18,19>5,99, tai apskaičiuotoji regresijos lygtis yra reikminė.

Determinacijos koeficientas rodo, kad 75,21% vieneto ilaidų priklauso nuo pardavimo apimties.

Liekamoji paklaidos dispersija

5. Daugiamačio regresijos modelio samprata

Vienmatės koreliacijos atveju nagrinėtas vieno iėjimo kintamojo - y ir vieno įėjimo kintamojo - x ryys. Praktikai pasitaiko daug u˛davinių, kur reikia nustatyti y priklausomybę nuo p įėjimo kintamųjų (x₁,x₂ ,, x_p). Kuo įėjimo kintamųjų daugiau, tuo modelį sudaryti darosi sunkiau, atsiranda papildomų tyrimo aspektų.

Daugiamatį koreliacijos ryį nusako is modelis:

. (22)

Bendruoju atveju daugiamatės regresijos modelis u˛raomas:

. (23)

Kai nagrinėjamas tik tiesinis koreliacijos ryys (ekonominėje analizėje to visai pakanka), gauname daugiamatį tiesinį regresijos modelį:

. (24)

Nagrinėjant daugiamačius regresijos modelius, apskaičiuojami tiesinės koreliacijos koeficientai:

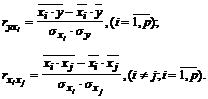(25)

Tiesinės koreliacijos koeficientai vadinami poriniais koreliacijos koeficientais, jiems būdingas simetrikumas,.

Porinių koreliacijos koeficientų reikmingumas tikrinamas analogikai kaip ir vienmatės regresijos atveju, pagal Stjudento kriterijų (7 formulė).

Reikminiai poriniai koreliacijos koeficientai u˛raomi į koreliacijos koeficientų matricą R, kuri yra kvadratinė ir simetrinė:

x_p

Kai koreliacija daugiamatė, dviejų kintamųjų ryį gali veikti ne tik jų tarpusavio sąveika, bet ir kiti kintamieji. Daliniai koreliacijos koeficientai kaip tik ir nustato ryio stiprumą tarp dviejų kintamųjų, kai kitų veiksnių įtaka eliminuota. Gautąsias dalinių koreliacijos koeficientų reikmes kartais galima paaikinti, remiantis ekonominiais samprotavimais.

Daliniai koreliacijos koeficientai nustatomi taip:

; (26)

čia R_ij, R_ii, R_jj – matricos R elementų r_ij, r_ii, r_jj algebriniai papildymai.

Dalinių koreliacijos koeficientų reikmingumas tikrinamas pagal Sjudento kriterijų:

; (27)

čia m – įvertinamų koreliacijos koeficientų skaičius.

Jei daliniai koreliacijos koeficientai nurodo glaudų tiesinį x_i ir x_j ryį, tai vieno įėjimo toliau nebereikia nagrinėti.

Daugiamatis koreliacijos koeficientas nustatomas taip:

; (28)

čia - matricos R determinantas; R₀₀ – r₀₀-ojo elemento algebrinis papildymas.

is koeficientas kinta nuo 0 iki 1. Kai r=0, tai tiesinė regresijos priklausomybė neegzistuoja.

Esant dviem įėjimams, x₁, x₂ (p=2), daugiamatis koreliacijos koeficientas nustatomas taip:

. (29)

Kai įėjimo kintamųjų skaičius p>3, derėtų remtis tokia daugiamačio koreliacijos koeficiento nustatymo formule:

; (30)

čia – standartizuoti regresijos koeficientai.

Paprastai randami pagal tokią lygčių sistemą:

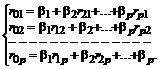(31)

Daugiamačio koreliacijos koeficiento reikmingumas tikrinamas pagal Fierio kriterijų (10 formulė).

Paprastai daugiamačiame tiesinės regresijos modelyje (24) reikia nustatyti (p-1) regresijos koeficientą:

;

koeficientai b₁, b₂,...b_j. ., b_p randami i p lygčių sistemos, kur j-oji lygtis nustatoma taip:

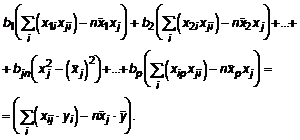(32)

Atskirų apskaičiuotų regresijos koeficientų reikmingumas tikrinamas pagal Stjudento kriterijų:

. (33)

Nereikminiai b_i atmetami.

Koeficiento b_i vidutinis nukrypimas:

(34)

;

Koeficientai c_ii randami i stebėjimo matricos diagonalinių elementų.

Liekamosios paklaidos, regresinės lygties bei įvertinimo paklaidos dispersijos apskaičiuojamos analogikai kaip ir vienmatės regresijos. Visos apskaičiuotosios lygties reikmingumas tikrinamas pagal Fierio kriterijų (19 formulė).

Daugiamačiame regresijos modelyje, analogikai kaip ir vienmačiame, yra determinacijos koeficientas, kuris nustatomas pagal 3 formulę.

Be bendrojo determinacijos koeficiento, yra daliniai determinacijos koeficientai D₁, D₂, , D_n, kurie rodo, kokią variacijos dalį nulemia atitinkami įėjimo kintamieji.

6. Daugiamatės regresijos lygties optimalaus dyd˛io nustatymas

Atliekant konkrečius regresijos modelio parametrų įvertinimo skaičiavimus, nustatyta, kad lygties pagrindimui nepakanka vien ˛inoti daugiamatį koreliacijos koeficientą, bet reikia patikrinti pagal Stjudento kriterijų ir kiekvieno koeficiento reikmingumą. Tokia skaičiavimo seka sudėtinga, nes, tik atlikęs visus sudėtingus skaičiavimus, gauname regresijos lygtį. Ar negalima ankstesniuose skaičiavimo etapuose patikrinti atskirų įėjimo kintamųjų reikmingumą ir kartu suma˛inti skaičiavimo apimtį?

is u˛davinys sprend˛iamas Helvigo metodu, leid˛iančiu nustatyti kiekvieno įėjimo kintamojo x_j papildomą įnaą į skirtingų veiksnių kombinacijų iėjimo kintamojo pasikeitimą.

Įėjimo kintamasis x_jteikia daugiau informacijos apie y kitimą, pirma, jei jo koreliacijos koeficientas artimas vienetui ir, antra, jei jis ma˛iau koreliuotas su kitais įėjimo kintamaisiais.

Įėjimo kintamojo x_jteikiamos informacijos apimtį nusako dydis g_j:

. (35)

iam dyd˛iui visuomet galioja . Dydis g_j lygus 0 tada, kai x_j yra isamios informacijos apie y kitimą indikatorius. Ir g_j=1, kai x_jnesuteikia papildomos informacijos apie y kitimą.

Įėjimo kintamojo x_jteikiamos informacijos kiekis nustatomas taip:

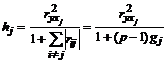. (36)

Suminis atskirų įėjimo kintamųjų kombinacijų informacijos kiekis nustatomas taip:

; (37)

čia k – įėjimo kintamųjų kombinacijų eilės numeris.

Dydis H_k kinta nuo 0 iki 1. Jei H_k artimas vienetui, tai k-oji įėjimo kintamųjų kombinacija teikia beveik isamią informaciją apie y kitimą. Tuomet tinkamiausia tiesinės daugiamatės regresijos lygtis atrenkama taip:

. (48)

iuo metodu ir spręsime konkretų u˛davinį.

U˛davinys. Tarkime, kad yra ˛inoma koreliacijos matrica (˛r. 4 lentelę), kurios visi poriniai koreliacijos koeficientai reikminiai:

4 lentelė

Koreliacijos matrica

Sprendimas. Norint rasti kiekvienos galimos regresijos lygties informacijos kiekį, sudaromos visos galimos įėjimo kintamųjų kombinacijos:

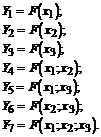
Apskaičiuojamas kiekvienos kombinacijos informacijos kiekis:

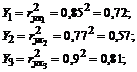
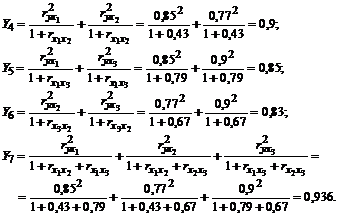
Geriausia yra septintoji regresijos lygtis, apimanti visus tris įėjimus.

7. Daugiamatis tiesinės regresijos modelis

Daugiamačio tiesinės regresijos modelio sudarymo struktūrinė schema pateikta 7 paveiksle.

U˛davinys. į daugiamatį tiesinį modelį modelį sudarysime, spręsdami konkretų u˛davinį, kurio statistiniai duomenys pateikti 5 lentelėje.

5 lentelė

Statistiniai duomenys

Eil. Nr.	y	x	x	x

7 pav. Daugiamačio tiesinės regresijos modelio sudarymo struktūrinė schema

Sprendimas. Remiantis iais pradiniais duomenimis, apskaičiuojami statistikos įvertinimai:

Apskaičiuojami poriniai koreliacijos koeficientai:

;

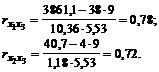
Apskaičiuotų porinių koreliacijos koeficientų reikmingumas patikrinamas, pasitelkus Stjudento kriterijų:

Patikrinamas ma˛iausio porinio koreliacijos koeficiento reikmingumas:

Tai rodo, kad visi poriniai koreliacijos koeficientai yra reikminiai.

Sudaroma koreliacijos koeficientų matrica:

Daliniai koreliacijos koeficientai apskaičiuojami tarp įėjimo kintamųjų x_i ir x_j, tad matricą R reikėtų pertvarkyti, ibraukiant y stulpelį ir y eilutę. Pertvarkyta matrica:

;

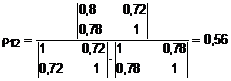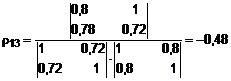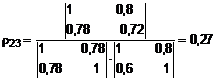Patikriname apskaičiuotų dalinių koreliacijos koeficientų reikmingumą:

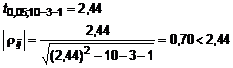Kaip matyti, visi daliniai koreliacijos koeficientai yra nereikminiai, o tai rodo, kad tarp įėjimo kintamųjų nėra glaudaus ryio ir nė vieno jų ibraukti nereikia.

Standartinių regresijos koeficientų apskaičiavimui sudaroma lygčių sistema:

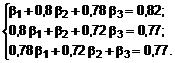
Isprendę ią lygčių sistemą, gauname:

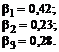
Daugiamatės koreliacijos koeficientas nustatomas taip:

io koeficiento reikmingumas patikrinamas pagal Fierio kriterijų:

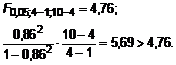
Kaip matome, daugiamatis koreliacijos koeficientas yra reikminis, ir verta apskaičiuoti daugiamatės tiesinės regresijos lygties koeficientus, kurie nustatomi i lygčių sistemos:

Isprendę lygčių sistemą, gauname:

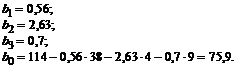
Tada regresijos lygtis yra tokia:

Norint nustatyti visos lygties reikmingumą, būtina apskaičiuoti paklaidų dispersiją. Skaičiuojame pagal regresijos lygties iėjimo reikmes. Skaičiavimo duomenys pateikti 6 lentelėje.

6 lentelė

Paklaidų apskaičiavimo duomenys

	y_i










a

Regresijos lygties paklaidos dispersija

Liekamosios paklaidos dispersija

Vertinimo paklaidos dispersija

Tada apskaičiuotos regresijos lygties reikmingumas tikrinamas pagal Fierio kriterijų:

Kadangi faktika Fierio kriterijaus reikmė didesnė u˛ teorinę, tai apskaičiuotoji regresijos lygtis yra reikminė.

Bendras determinacijos koeficientas

Tai rodo, kad 73,96% y kitimo lemia, x₁, x₂, x₃ kitimas. Lieka neįvertinta 26,04% y kitimo.

Politica de confidentialitate | Termeni si conditii de utilizare

DISTRIBUIE DOCUMENTUL

Vizualizari: 3038
Importanta:

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Distribuie URL
https://www.scrigroup.com/limba/lituaniana/253/Regresijos-modeliai-Regresijos93852.php

Adauga cod HTML in site
<a href="https://www.scrigroup.com/limba/lituaniana/253/Regresijos-modeliai-Regresijos93852.php" target="_blank" title=" - https://www.scrigroup.com/limba/lituaniana/253/Regresijos-modeliai-Regresijos93852.php">Regresijos modeliai - Regresijos modelio samprata</a>