Jungumas

Jungumas

Jungusis grafas – tai grafas, kuriame bet kuri viršūnių pora sujungta grandine. Pavyzdžiui, (žr. 1 pav.) K₅ ir C₅ yra jungieji grafai, tačiau intuityviai jaučiame, kad K₅ yra labiau jungus nei C₅.

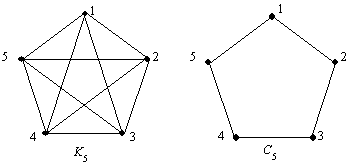
1 pav. Jungumas

Grafo jungumo klausimas yra aktualus praktikoje. Tarkime, reikia suprojektuoti kompiuterių tinkl¹. Tinkl¹ sudaro informacijos saugojimo ir apdorojimo centrai, kurie jungiami ryšio kanalais. Informacijos pasikeitimas tarp dviejų centrų vyksta arba tiesiogiai per šiuos centrus jungiantį ryšio kanal¹ (jei toks yra), arba per kitus centrus ir juos jungiančius ryšio kanalus. Aišku, kad tinklo grafas, kurio viršūnės vaizduoja centrus, o dvi viršūnės jungiamos briauna, jei tarp viršūnėms atitinkančių centrų yra ryšio kanalas, turi būti jungusis. Labai svarbus tinklo parametras yra jo patikimumas: tinklas turi funkcionuoti net ir tuo atveju, jei sugenda keli centrai arba ryšio kanalai. Šį parametr¹ kiekybiškai galima įvertinti per žemiau įvestas s¹vokas.

Viršūninio jungumo skaičius. Tai mažiausias skaičius viršūnių, kurias pašalinus, grafas G tampa arba nejungiuoju grafu arba vienos viršūnės grafu. Šis skaičius žymimas .

Briauninis jungumo skaičius. Tai mažiausias skaičius briaunų, kurias pašalinus, grafas G tampa nejungiuoju grafu. Šis skaičius žymimas .

Pavyzdžiui, , .

2 pav. grafui (pašalinus 4-¹j¹ viršūnź, grafas suyra), o (pašalinus briaunas (4, 6), (4, 7), (4, 8) grafas suyra).

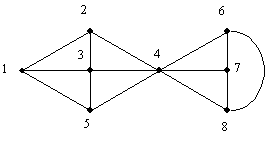
2 pav. Grafo jungumo kiekybiniai įverčiai

Grafo G viršūnė v vadinama s¹lyčio tašku, jei G – v turi daugiau jungiųjų komponenčių nei grafas G.

Grafo G briauna vadinama tiltu, jei, j¹ pašalimus, gautasis grafas turi daugiau jungiųjų komponenčių nei grafas G.

Pavyzdžiui, 3 pav grafas turi tris s¹lyčio taškus (viršūnės 4, 5, 6) ir vien¹ tilt¹ (briauna (4, 5)).

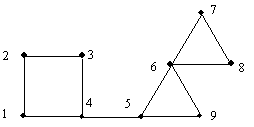
3 pav. Grafo s¹lyčio taškai ir tiltai

Grįžtant prie paragrafo pradžioje pateikto pavyzdžio, nesunku pastebėti, kad grafo viršūninio jungumo ir briauninio jungumo skaičius parodo tinklo atsparum¹ centrų ir ryšio kanalų gedimams, o s¹lyčio taškai bei tiltai parodo labiausiai pažeidžiamas tinklo vietas.

Teorema. Kiekvienam grafui

čia , o – v-osios viršūnės laipsnis.

Teorema. Beveik kiekvienam grafui[6] teisinga lygybė

Grafas vadinamas k-jungiuoju, jei ir briaunomis k-jungiuoju, jei .

Jei , tai grafas vadinamas dviryšiu

2 pav. pavaizduotas grafas yra 1-jungusis ir briaunomis –
3-jungusis. Ai ku, kad šis grafas turi pografius, kurie yra labiau jungieji nei pats grafas. Pavyzdžiui, pografis, kurį indukuoja viršūnių aibė, yra 3-jungusis. Tokių pografių apibūdinimui įvedama k-jungiosios komponentės s¹voka.

Grafo k-jungioji komponentė – tai maksimalus k-jungusis pografis. Jis dažnai vadinamas k-komponente.

Pavyzdžiui, 4 pav. grafas G₁ turi dvi 2-jungi¹sias komponentes (pografiai, kuriuos indukuoja viršūnių ir aibės), o grafas G₂ turi dvi 3-komponentes (pografiai, kuriuos indukuoja viršūnių ir aibės). Tačiau reikia pabrėžti, kad abu grafai G₁ ir G₂ yra 1-jungieji. Be to, nesunku pastebėti, kad dvi 2-komponentės turi vien¹ bendr¹ viršūnź (Grafe G₁ – tai 3-ioji viršūnė), o dvi 3-komponentės turi dvi bendras viršūnes (grafe G₂ – tai 4-oji ir 6-oji viršūnės).

Teorema. Dvi skirtingos grafo G k-komponentės turi ne daugiau nei bendrų viršūnių.

Apibrėžimas. Dvi -grandinės vadinamos nesusikertančiomis (viršūnėmis nesusikertančiomis), jei jos neturi bendrų viršūnių, išskyrus a ir b.

Teorema (H.Witney, 1932). Grafas yra k-jungusis tada ir tiktai tada, kai bet kuri nesutampančių viršūnių pora sujungta ne mažiau kaip k viršūnėmis nesusikertančių grandinių.

Apibrėžimas. Sakoma, kad grafo G viršūnių poaibis S skiria viršūnes a ir b, jei grafe viršūnės a ir b priklauso skirtingoms jungiosioms komponentėms.

4 pav. Grafo k-komponentės

Teorema (K.Mengeras, 1927). Mažiausias skaičius viršūnų, skiriančių dvi negretimas viršūnes a ir b, yra lygus didžiausiam skaičiui poromis nesusikertančių grandinių, jungiančių a ir b viršūnes.

Įveskime skiriančių briaunų s¹vok¹.

Apibrėžimas. Briaunų aibė R skiria grafo G a ir b viršūnes, jei grafe viršūnės a ir b priklauso skirtingoms jungiamosioms komponentėms.

Teorema. Mažiausias skaičius briaunų, skiriančių grafo G viršūnes a ir b, yra lygus didžiausiam briaunomis nesusikertančių grandinių, jungiančių a ir b viršūnes, skaičiui.

Dviryšiai grafai

Tiek grafų teorijoje, tiek ir praktikoje svarbi¹ viet¹ užima 2-jungieji grafai, kurie vadinami dviryšiais grafais.

Kaip buvo minėta aukščiau, grafas yra dviryšis, jei bet kuri¹ nesutampančių viršūnių a ir b por¹ jungia bent dvi viršūnėmis nesusikertančios grandinės.

Galima pateikti ir kit¹ dviryšio grafo apibrėžim¹: grafas vadinamas dviryšiu, jei jis neturi s¹lyčio taškų.

Apibrėžimas. Didžiausias galimas grafo G pografis, neturintis s¹lyčio taškų, vadinamas dvigubo jungumo komponente arba bloku.

Grafo dvigubo jungumo komponenčių bei s¹lyčio taškų ieškojimo uždavinys turi svarbi¹ reikšmź. Pavyzdžiui, visi komunaliniai ir transporto tinklai negali turėti s¹lyčio taškų, t.y. mažiausiai jie turi būti dviryšiai.

Dvigubo jungumo komponenčių išskyrimas grafe padeda sprźsti nepriklausomų ciklų radimo uždavinį bei nustatyti, ar grafas yra plokštusis.

Aptarsime grafo dvigubo jungumo komponenčių (dviryšių komponenčių, blokų) radimo uždavinį.

S¹lyčio taško savybė. Neorientuotojo jungiojo grafo G viršūnė a yra s¹lyčio tašku tada ir tiktai tada, kada egzistuoja tokios kitos dvi grafo viršūnės x ir y, kad bet kuris kelias tarp viršūnių x ir y eina par viršūnź a.

Pavyzdžiui, 5 a) pav. Pavaizduotas grafas G, o 5 b) pav. – to grafo dvigubo jungumo komponentės.

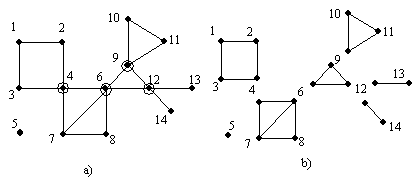
5 pav. Grafo dvigubo jungumo komponentės

Ši s¹lyčio taško savybė įgalina panaudoti paieškos gilyn metod¹, apskaičiuojant grafo G dvigubo jungumo komponentes – blokus.

Panagrinėkime pavyzdį (žr. 6 pav.).

6 pav. Grafo blokinė schema

6 pav. schematiškai vaizduoja jungųjį graf¹, susidedantį iš 9-ių dvigubo jungumo komponenčių bei turintį 5-is s¹lyčio taškus v₁, v₂, v₃, v₄, ir v₅.

Tarkime, kad paiešk¹ gilyn pradėjome iš 9-ojo bloko G₉ viršūnės s, ir visas aplankytas viršūnes (briaunas) talpiname į stek¹ STEK. Pradėjź paiešk¹ iš viršūnės s, per viršūnź v₂ galime patekti į blok¹ . Remiantis paieškos gilyn savybe, kad per viršūnź v₂ grįšime, kai bus aplankytos visos viršūnės, galime teigti, kad sudaro viršūnės (briaunos), kurios buvo aplankytos tarp įėjimo ir grįžimo per viršūnź v₂.

Su kitomis dvigubo jungumo komponentėmis reikalas sudėtingesnis. Iškeliavź iš viršūnės s, galime patekti į jungumo komponentź G₃, o iš G₃ per viršūnź v₃ – patekti į komponentź G₂. Tačiau ir šiuo atveju, kai aplankytos viršūnės (briaunos) saugomos steke STEK, grįžtant per viršūnź v₃, visos aplankytos bloko G₂ viršūnės bus steko viršuje (nuo steko viršaus iki viršūnės v₃). Pašalinus iš steko šias viršūnes, steko viršuje liks bloko G₃ viršūnės, kurios buvo aplankytos iki patekome į blok¹ G₂. Kai grįšime į viršūnź v₂, steko viršuje bus visos bloko G₃ viršūnės.

Vadinasi, jei mokėtume atpažinti s¹lyčio taškus, tai naudodami paiešk¹ gilyn ir saugodami aplankytas viršūnes (briaunas) steke ta tvarka, kuria jos buvo aplankytos, galime rasti dvigubo jungumo komponentes: viršūnės (briaunos), esančios steko viršuje grįžimo per s¹lyčio tašk¹ metu, sudaro dvigubo jungumo komponentź.

Aptarkime formali¹ s¹lyčio taškų radimo s¹lyg¹.

Tarkime, kad – jungusis neorientuotasis grafas. Tarkime, kad T – jį dengiantis medis su šaknimi r, sukonstruotas paieškos gilyn iš viršūnės r metodu.

1 lema. Šaknis r yra s¹lyčio taškas tada ir tiktai tada, kai r turi daugiau nei vien¹ sūnų (žr. 7 pav.).

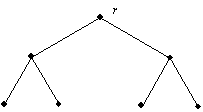
7 pav. Dengiančio medžio T šaknis r – s¹lyčio taškas

2 lema. Viršūnė yra grafo s¹lyčio taškas tada ir tiktai tada, kai yra nors vienas viršūnės v sūnus r, kuris neturi atvirkštinių briaunų, jungiančių jį patį arba bet kurį jo palikuonį su viršūnės v protėviu (žr. 8 pav.).

Priminsime, kad grafo G atvirkštinės briaunos yra visos briaunos, nepriklausančios dengiančiojo medžio T briaunų aibei.

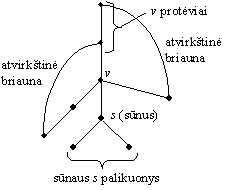
8 pav. Dengiančio medžio T viršūnė v – s¹lyčio taškas

S¹lyčio taškams rasti kiekvienai grafo viršūnei v įvesime du parametrus: ir .

Parametras yra viršūnės v aplankymo eilės numeris, atliekant paiešk¹ gilyn iš viršūnės r.

Parametras [7] – tai mažiausias aplankymo numeris viršūnės x, į kuri¹ galime patekti iš viršūnės v grandine, sudaryta iš nulio arba daugiau dengiančio medžio briaunų ir nedaugiau kaip vienos atvirkštinės briaunos (žr. 9 pav.).

9 a) pav. pavaizduotas grafas G, o 9 b) pav. pavaizduotas t¹ graf¹ dengiantis medis, sukonstruotas paieškos gilyn iš 1-osios viršūnės metodu. Medžio briaunos pavaizduotos ištisine, o atvirkštinės briaunos – punktyrine linija. Romėniškais skaičiais pažymėti viršūnių aplankymo eilės numeriai, o parametro reikšmės apibrėžtos.

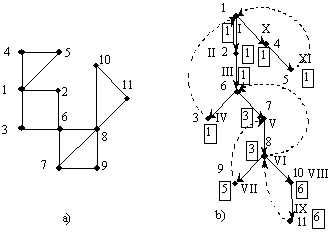
9 pav. Parametrų nr[v] ir low[v] reikšmės

Pasinaudodami parametrais ir galima 2 lemos kriterijų perrašyti kaip teorem¹.

Teorema. Viršūnė yra grafo G s¹lyčio taškas tada ir tiktai tada, kai v turi sūnų s, kuriam .

Pavyzdžiui, 9 a) pav. grafui s¹lyčio taškai yra: 1-oji viršūnė (medžio šaknis, turinti du sūnus), 6-oji viršūnė (ji turi sūnų , kuriam ) ir 8-oji viršūnė (ji turi sūnų , kuriam ).

Bendresnis pavyzdys pateiktas 10 paveiksle. Čia 10 a) pav. duotas grafas, o 10 b) – jį dengiantis medis, sukonstruotas naudojant paiešk¹ gilyn iš 1-osios viršūnės. Simbolių prie medžio reikšmės tos pačios, kaip ir 9 b) pav. Remiantis aukščiau pateiktu nagrinėjimu, nesunku apskaičiuoti, kad šio grafo s¹lyčio taškai yra: 1-oji viršūnė (šaknis, turinti du sūnus), 6-oji viršūnė (sūnaus parametras ), 8-oji viršūnė (turi du sūnus ir , kurių ) ir 11-oji viršūnė (sūnaus ).

Parametr¹ galima apibrėžti rekurentiškai:

low[v] = min (nr[v]; low[s], čia s – viršūnės v sūnus; nr[w], čia (v, w) – atvirkštinė briauna).

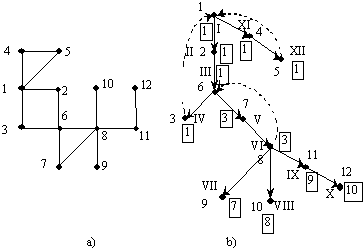
10 pav. S¹lyčio taškų apskaičiavimas

Remiantis šiuo apibrėžimu, reikšmė apskaičiuojama taip.

Kai viršūnė v paieškos gilyn metu yra aplankoma pirm¹ kart¹, tai

Kai nagrinėjama atvirkštinė briauna , tai .

Kai grįžtame į viršūnź v, pilnai apėjus visas briaunas, incidentiškas sūnui s, tai .

Kai grįžtame į viršūnź v, pilnai apėjus visas briaunas, incidentiškas sūnui s, tai reikšmė nusistovi. Jei šiuo metu , tai, pagal teorem¹, v yra s¹lyčio taškas.

Žemiau pateikta dvigubo jungumo komponenčių ieškojimo procedūra, kurios pagrind¹ sudaro paieškos gilyn algoritmas, išnagrinėtas 2.8.1.2 paragrafe, ir kuris papildytas aukščiau aptartu s¹lyčio taškų s¹lygos tikrinimu bei blokų formavimu.

const c

type

mas = array [1..c] of integer;

matr = array [1..2, 1..c] of integer;

procedure blok (n, m : integer; L, lst : mas; var st : mas);

var i, k, u : integer;

s, sk, tau : integer;

t, p, pirma : boolean;

fst, prec : mas;

stek : mas;

nr, low : mas;

begin

pirma := false;

v

nr [v] := 1;

low [v] := 1;

sk

tau

for i := 1 to n do begin

fst [i]:= lst [i] + 1;

prec [i] := 0;

st [i] := 0;

end

k := v;

if fst [k] <= lst [k + 1] then

begin

t := false;

p := true;

prec [k] := k;

end

else

t := true;

while not t do

begin

while p do

begin

u := L [fst [k]];

if prec [u] = 0 then

begin

sk := sk +1;

nr [u] := sk;

low [u] := nr [u];

tau := tau + 1;

stek [tau] := k;

tau := tau + 1;

stek [tau] := u;

prec [u] := k;

if fs t [u] <= lst [u + 1] then

k := u

else

p := false;

end

else

begin

if (prec [k] <> u) and (nr [k] > nr[u]) then

begin

tau := tau + 1;

stek [tau] := k;

tau := tau + 1;

stek [tau] := u;

if nr [u] < low [k] then low [k] := nr [u];

end

p := false;

end

end

while not p and not t do

begin

fst [k] := fst [k] + 1;

if fst [k] <= lst [k + 1] then

begin

if k = 1 then

pirma := true;

p := true;

end

else

if prec [k] = k then

t := true

else

begin

s := k;

k := prec [k];

if low [s] < low [k] then low[k]:=low[s];

if ((k <> 1) and (low [s] >= nr [k])) or ((k = 1) and pirma) then

begin

st[k] := 1;

writeln ('s¹l. taškas = ', k : 3);

end

if low [s] >= nr [k] then

begin

writeln ('blokas');

while (stek [tau] <> s) or (stek [tau – 1] <> k) do

begin

write (stek [tau] : 3,' - ',

stek [tau – 1] : 3);

tau := tau – 2;

writeln

end

write (stek [tau] : 3,' – ',

stek [tau – 1] : 3);

tau := tau – 2;

writeln

end

end

end

end

end;

Srautai tinkluose ir giminingi uždaviniai

Pagrindinės s¹vokos

Aptarsime kelis praktinių uždavinių pavyzdžius.

Pirmas pavyzdys. Tarkime, kad turime tinkl¹ automobilinių kelių, kuriais galima nuvykti iš punkto A į punkt¹ B. Keliai gali kirstis tarpiniuose punktuose. Kiekvienai kelio atkarpai yra žinomas maksimalus skaičius automobilių, kuriuos ši kelio atkarpa gali praleisti per laiko vienet¹ (kelio pralaidumas). Koks didžiausias skaičius automobilių per laiko vienet¹ gali nuvažiuoti iš punkto A į punkt¹ B? Šis automobilių skaičius vadinamas nagrinėjamo kelio tinklo automobilių srauto dydžiu. Paparastai mus domina ne vien tik koks didžiausias automobilių skaičius gali nuvykti iš A į B, bet ir kiekvieno kelio ruožo srautas, t.y. koks skaičius automobilių vyksta šiuo kelio ruožu.

Aišku, kad galimas ir kitas klausimas: kiek ir kokių kelių pralaidumus reikia padidinti, kad maksimalus automobilių srautas per šį kelių tinkl¹ padidėtų nurodytu dydžiu?

Antras pavyzdys. Tarkime, kad naftos verslovė A naftotiekių tinklu yra sujungta su perdirbimo įmone B. Taip pat žinome kiekvieno naftotiekio tarpo maksimalų pralaidum¹ – debit¹ (naftos kiekį per laiko vienet¹). Kokį kiekį naftos per laiko vienet¹ galime perpumpuoti šiuo tinklu?

Trečias pavyzdys. Turime informacijos perdavimo tinkl¹. Žinomas kiekvienos ryšio linijos pralaidumas. Kokį didžiausi¹ informacijos kiekį šiuo tinklu galima perduoti iš punkto A į punkt¹ B?

Šie ir daugelis kitų praktinių uždavinių nagrinėjami srautų tinkluose teorijos metodais. Šiame paragrafe sprźsime pagrindinį šios teorijos uždavinį – maksimalaus srauto radimo uždavinį.

Apibrėžimas. Tinklas, tai pora , kur pirmasis poros elementas yra bet koks orientuotasis grafas, kuriame išskirtos dvi viršūnės s ir t, iš kurių pirmoji viršūnė s, neturinti įeinančių lankų, vadinama šaltiniu, o antroji – t, neturinti išeinančių lankų, vadinama nuotakiu. Antrasis poros elementas C yra funkcija , kuri kiekvienam lankui priskiria neneigiam¹ realųjį skaičių , kuris vadinamas lanko pralaidumu.

Apibrėžimas. Tarkime, kad duota funkcija . Tada funkcijos f divergencija viršūnėje v vadinamas dydis , apibrėžiamas formule:

(1)

Jei interpretuosime kaip sraut¹ iš viršūnės u į viršūnź v, tai skaičius parodo “srauto kiekį”, kuris išeina iš viršūnės v. Šis skaičius gali būti teigiamas (jei iš viršūnės v daugiau išeina negu įeina, t.y. viršūnė v yra papildomas šaltinis), neigiamas (jei į viršūnź v daugiau įeina negu išeina, t.y. srautas kaupiasi viršūnėje v) ir lygus nuliui.

Apibrėžimas. Funkcija vadinama srautu tinkle S, jeigu:

kiekvienam grafo G lankui galioja nelygybė

(2)

kiekvienos viršūnės v, išskyrus s ir t, divergencija lygi nuliui, t.y.

(3)

Skaičius vadinamas srauto dydžiu.

Pagal šį apibrėžim¹ nagrinėjame sraut¹, kuris nesikaupia ir neatsiranda nei vienoje tarpinėje grafo G viršūnėje (išskyrus viršūnes s ir t).

Toliau sprźsime maksimalaus srauto radimo uždavinį: rasime toki¹ funkcij¹ , kuri tenkintų (2) ir (3) apribojimus ir kuriai skaičius būtų didžiausias. Aišku, kad funkcijos f reikšmės kiekvienam lankui apibrėš maksimalų sraut¹ per šį lank¹.

Maksimalaus srauto apskaičiavimo uždavinys yra tiesinio programavimo uždavinys, todėl jam gali būti taikomi tiesinio programavimo uždavinių sprendimo metodai. Tačiau, įvertinant uždavinio specifik¹, yra sukurti žymiai efektyvesni šio uždavinio sprendimi metodai, kuriuos toliau ir nagrinėsime.

Pjūvio apibrėžimas. Tinklo S pjūviu , kurį apibrėžia grafo G viršūnių tikrinis poaibis A, t.y. ir ir , vadiname grafo G tokių lankų aibź, kad , o .

Kitaip tariant,

Aišku, kad bet kokiam tinklo S srautui f pjūvio srautas yra lygus pjūvį sudarančių lankų sumai, t.y.

Lema. Jei , o , tai bet kokiam srautui f iš s į t galioja lygybė

(4)

Įrodymas. (4) lygybės teisingumas išplaukia iš (1) ir (3) formulių.

Susumuokime (3) lygtis visoms grafo viršūnėms . Ši¹ sum¹ sudarys nariai , turintys pliuso arba minuso ženkl¹.

Jei abi viršūnės u ir v priklauso aibei A, tai turės pliuso ženkl¹ lygtyje ir minuso ženkl¹ lygtyje , ir šio dėmens neturės nei viena lygtis , kai ir . Vadinasi, sumuodami šiuos dėmenis, gausime 0.

Jei , o , tai kiekvienas narys sumoje pasikartos vienintelį kart¹ su ženklu plius lygtyje , ir visumoje gausime . Analogiški dėmenys , kai , o , duos (4) formulės narį . Kita vertus, nagrinėjama suma lygi , nes visiems .

Išvada. .

Imdami iš (4) formulės gausime:

Gauta tapatybė įrodo intuityviai aiškų fakt¹: nuotakio srautas yra lygus šaltinio srautui.

Įrodyta lema sako tai, kad tinklo srautas gali būti matuojamas bet kuriame pjūvyje, kuris atskiria s ir t viršūnes.

Pavyzdys. 1 pav. pavaizduotas tinklas. Skaičiai prie lankų apibrėžia sraut¹ f. Lankų pralaidum¹ žymi skliausteliuose parašyti skaičiai. Panagrinėkime pjūvius, kuriuos nusako viršūnių ir poaibiai.

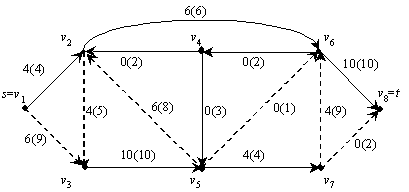
1 pav. Srautas tinkle: 1-osios lemos ir didinančiosios grandinės iliustracija. Punktyru išskirta didinančioji grandinė.

Aibės A viršūnių divergencija yra:

Šias lygtis sudėjź, gausime:

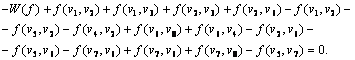
Sutraukź panašius narius, gausime:

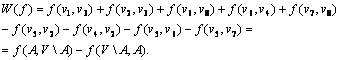
Įstatź srauto reikšmes, gausime:

Pjūviui, kurį nusako poaibis , analogiškai gausime:

Įstatź srauto reikšmes, gausime:

Nesunku pastebėti, kad šie pavyzdžiai iliustruoja lemos įrodym¹ bei lemos išvados teisingum¹.

Apibrėžimas. Pjūvio, kurį nusako viršūnių poaibis A, t.y. pjūvio pralaidumas yra skaičius, apibrėžiamas formule

Kitaip tariant, pjūvio pralaidumas yra lygus pjūvį sudarančių lankų pralaidumų sumai.

Apibrėžimas. Minimaliu pjūviu vadinsime pjūvį , kurio pralaidumas yra mažiausias tarp visų galimų pjūvių, atskiriančių s ir t viršūnes.

Vienas iš pagrindinių srautų tinkluose rezultatų yra nusakomas Fordo ir Falkersono teorema.

Teorema (Fordas (Ford L.R.) ir Falkersonas (Fulkerson D.R.) 1962). Bet kokio srauto iš viršūnės s į viršūnź t dydis neviršija minimalaus pjūvio, skiriančio šias viršūnes, pralaidumo; be to egzistuoja toks srautas, kurio dydis yra lygus tokio minimalaus pjūvio pralaidumui.

Įrodymas. Tarkime, kad – minimalus pjūvis. Remiantis lema, bet kokiam srautui f gausime:

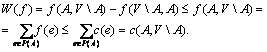
Įrodymas, kad maksimalaus srauto dydis yra lygus minimalaus pjūvio pralaidumui, yra sudėtingesnis faktas. Šis įrodymas išplauks iš maksimalaus srauto konstravimo algoritmo, kuris nagrinėjamas kitame paragrafe.

Maksimalaus srauto konstravimo algoritmas

Visi žinomi maksimalaus srauto konstravimo algoritmai pagrįsti nuosekliu srauto didinimo metodu, o visų srauto didinimo metodų pagrind¹ sudaro didinančiųjų grandinių teorija.

Apibrėžimas. Tinklo S lankas e iš viršūnės u į viršūnź v vadinamas leistinuoju lanku srauto f atžvilgiu, jeigu

a)    ir

arba

b)   ir .

Jei galioja s¹lyga a), tai tokį lank¹ vadinsime suderintuoju (soglasovannaja duga). Jei galioja s¹lyga b), tai tokį lank¹ vadinsime nesuderintuoju (nesoglasovannaja duga).

Apibrėžimas. Ilgio l didinančioji grandinė iš viršūnės s į viršūnź t srauto f atžvilgiu yra seka, sudaryta iš besikeičiančia tvarka surašytų (poromis skirtingų) viršūnių ir lankų:

(5)

Čia , ir kiekvienam lankas srauto f atžvilgiu yra leistinasis lankas iš viršūnės į viršūnź .

Pavyzdžiui, 1 pav. pavaizduoto tinklo ir srauto per jį atžvilgiu, grandinė:

(6)

yra didinančioji grandinė, kurios ilgis yra 6.

Žinodami (5) pavidalo didinanči¹j¹ grandinź, sraut¹ f galime padidinti dydžiu

čia

Tam tikslui (pavyzdžiui, žiūrint į 1 pav.) reikia didinančiosios grandinės kiekvieno suderintojo lanko sraut¹ padidinti dydžiu d, o kiekvieno nesuderintojo lanko sraut¹ sumažinti tuo pačiu dydžiu d, t.y.

Aišku, kad taip apskaičiuota funkcija yra srautas, nes , ; ir , .

Iš tikro, jei nepriklauso didinančiajai grandinei, tai .

Tarkime, kad priklauso didinančiajai grandinei. Tada (žr. 2 pav.):

jei ir yra suderintieji lankai, tai srautas, įtekantis į viršūnź ir ištekantis iš jos padidėja tuo pačiu dydžiu d ; tuo būdu (žr. 2 a) pav.),

jei ir yra nesuderintieji lankai, tai srautas, įtekantis ir ištekantis iš viršūnės sumažėja tuo pačiu dydžiu d ; vadinasi (žr. 2 b) pav.),

jei yra suderintasis lankas, o – nesuderintasis lankas, tai srautas įeinančiu į viršūnź lanku padidėja dydžiu d, o įeinančiu lanku sumažėja tuo pačiu dydžiu; vadinasi (žr. 2 c) pav.),

jei yra nesuderintasis lankas, o – suderintasis lankas, tai išeinančiu iš viršūnės lanku srautas sumažėja dydžiu d, o išeinančiu iš viršūnės lanku padidėja tuo pačiu dydžiu; tuo būdu (žr. 2 d) pav.).

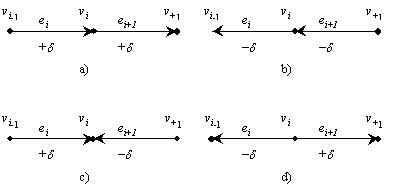
2 pav. Didinančiosios grandinės lankų, incidentiškų viršūnei v_i, srauto perskaičiavimas

Srauto dydis padidėja dėmeniu d

Pavyzdys. Panagrinėkime tinkl¹ su srautu f, kuris pavaizduotas 1 pav. (6) seka yra šio tinklo ir srauto per jį atžvilgiu didinančioji grandinė. Šiai grandinei

Vadinasi, 2. 17.1 pav. pavaizduoto tinklo sraut¹ galima padidinti dydžiu 1, t.y. nuo 10 iki 11. 3.17.3 pav. pavaizduotas tas pats 1 pav. tinklas ir perskaičiuotas srautas.

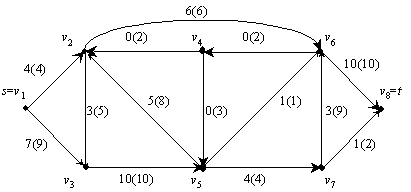
3 pav. Tinklo, pavaizduoto 1 pav., srautas po modifikacijos

Įrodysime teorem¹, kuri pagrindžia maksimalaus srauto apskaičiavimo, naudojant didinačiasias grandines, metod¹.

Teorema. Žemiau pateiktos trys s¹lygos yra ekvivalenčios:

srautas iš s į t maksimalus,

neegzistuoja didinančios grandinės srauto f atžvilgiu,

egzistuoja pjūvis, kurį nusako toks viršūnių poaibis , skiriantis viršūnes s ir t (, ), kad .

Įrodymas Þ 2). Jei srautas maksimalus, tai aišku, kad neegzistuoja didinančiosios grandinės šio srauto atžvilgiu, nes, priešingu atveju, esant didinančiai grandinei, sraut¹ būtų galima padidinti.

Þ 3). Tarkime, kad srautui f neegzistuoja didinančiosios grandinės. Apibrėžkime viršūnių aibź , kuri¹ sudaro viršūnės tokios grandinės

kad , , ir – leistinasis lankas iš viršūnės į viršūnź , . Aišku, kad , o , nes šiuo atveju egzistuotų didinančioji grandinė srauto f atžvilgiu. Panagrinėkime pjūvį . Iš aibės A ir suderintojo lanko apibrėžimo išplaukia, kad kiekvienam pjūvio lankui turi galioti lygybė . Vadinasi, .

Analogiškai, remiantis aibės A ir nesuderintojo lanko apibrėžimu, gausime, kad . Remiantis aukščiau įrodyta lema, gausime

Þ 1) išplaukia iš to fakto, kad srauto dydis nevišija .

Pavyzdys. Nesunku patikrinti, kad srautas 3 pav. yra maksimalus. “Prisotintas” pjūvis , atsirandantis teoremos įrodyme, yra .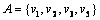

Remiantis pateiktais teoriniais samprotavimais, galima sudaryti paprast¹ maksimalaus srauto apskaičiavimo algoritm¹: pradėdami nuo bet kokio, pavyzdžiui, nulinio srauto (, ), ieškosime didinančiosios grandinės ir, jei tokia grandinė egzistuoja, sraut¹ didinsime; priešingu atveju srautas f yra maksimalus.

Tačiau čia iškyla klausimas, ar algoritmo žingsnių skaičius yra baigtinis. Fordas ir Falkersonas[8] davė neigiam¹ atsakym¹. 1962 m. jie pateikė pavyzdį tokio tinklo, kuriame galima taip parinkinėti didinančiasias grandines, kad procesas niekada nepasibaigtų. Be to, srauto dydis vis¹ laik¹ bus ketvirtadaliu mažesnis už maksimalaus srauto dydį.

Tačiau 1972 m. Edmondsas (Edmonds J.) ir Karpas (Karp R.M.)[9] įrodė, kad, jei kiekviename žingsnyje sraut¹ didinsime trumpiausios didinančiosios grandinės atžvilgiu, tai maksimalus srautas bus sukonstruotas, panaudojant ne daugiau kaip grandinių (čia , ). Rasti trumpiausi¹ didinanči¹j¹ grandinź patogu, naudojant paiešk¹ platyn (žr. 2.9 paragraf¹). Įvertinant tai, kad trumpiausios grandinės konstravimo algoritmo sudėtingumas yra , galime įvertinti viso maksimalaus srauto apskaičiavimo algoritmo sudėtingum¹, – .

Čia nenagrinėsime šio algoritmo detalių, kadangi toliau panagrinėsime efektyvesnį 1970 m. Dinico (Dinic E.A.)[10] pasiūlyt¹ maksimalaus srauto apskaičiavimo algoritm¹, kurio sudėtingumas yra .

Dinico metodas susideda iš fazių. Jo efektyvumas pagrįstas tuo, kad, nepriklausomai nuo tinklo lankų pralaidumo, fazių skaičius niekada neviršija , čia n – tinklo viršūnių skaičius [Lip88].

Panagrinėkime k-osios fazės veiksmus. Tarkime, kad fazės pradžioje turime tinkl¹ G ir jame apibrėžt¹ sraut¹ f. Tokį tinkl¹ žymėsime simboliu G_f.

Remdamiesi tinklu G_f, sudarome pagalbinį tinkl¹, kuris neturi kontūrų (ciklų) ir kurio struktūra vaizduoja visas trumpiausias didinančiasias tinklo G_f grandines. Pažymėkime šį tinkl¹ simboliu S_f. Tinklas S_f konstruojamas paieškos platyn grafe G_f metodu, ir į tinkl¹ S_f įtraukiami tinklo G_f srauto f atžvilgiu leistinieji lankai. Tuo būdu į tinkl¹ S_f įeina šaltinis s, nuotakis t ir grafo G_f leistinieji lankai , čia viršūnė u nutolusi nuo šaltinio s atstumu d, o viršūnė v – atstumu d+1, , o l yra tinklo S_f ilgis, t.y. atstumas nuo s iki t grafe G_f. Šio lanko pralaidum¹ žymėsime ir apibrėšime formule

Sudarius pagalbinį tinkl¹ S_f, toliau jame apskaičiuojamas pseudomaksimalus srautas.

Apibrėžimas. Ilgio l tinklo S_f pseudomaksimalus srautas – tai toks tinklo S_f srautas f ^*, prie kurio tinkle S_f neegzistuoja nei viena l ilgio didinančioji grandinė; kitaip tariant, bet kokiam tinklo S_f iš viršūnės s į viršūnź t keliui

egzistuoja toks lankas , kad

Po to pseudomaksimalus srautas “perkeliamas” į pagrindinį tinkl¹ G_f : srautas sumuojamas su G_f srautu ; jei ši suma iššaukia lanko “persipildym¹”, t.y. suma viršija , tai šis srauto “perteklius” kompensuojamas sumažinant sraut¹ . Tuo būdu viršūnės u divergencija padidėja dydžiu , o viršūnės v divergencija tuo pačiu dydžiu sumažėja. Nesunku įsitikinti, kad tokių visų lankų srautų modifikacija apibrėžia nauj¹ tinklo G_f sraut¹ , kurio dydis . Šiuo veiksmu ir baigiama k-oji fazė.

Maksimalaus srauto konstravimas baigiamas, kai iš tinklo G_f nebegalima sukonstruoti pagalbinio tinklo S_f.

Kaip bus matyti iš toliau pateiktų tinklo S_f bei jo pseudomaksimalaus srauto apskaičiavimo algoritmų, vienos fazės sudėtingumas yra . Kadangi, kaip parodyta literatūroje [Lip88], fazių skaičius neviršija , tai Dinico metodo sudėtingumas yra O(n³).

Pavyzdys. Panagrinėkime tinkl¹, pavaizduot¹ 4 a) paveiksle. Prie lanko parašytas skaičius reiškia lanko maksimalų sraut¹, o skaičius skliausteliuose rodo lanko pralaidum¹.

4 pav. Maksimalaus srauto ieškojimas Dinico metodu

Pradėjź nuo tinklo nulinio srauto , pirmiausia apskaičiuojame pagalbinį be kontūrų tinkl¹ S_f0 (žr. 4 b) pav.). Po to rast¹jį pseudomaksimalų sraut¹ perkeliame į tinkl¹ , gaudami sraut¹ , t.y. tinkl¹ G_f1.

Toliau konstruojame pagalbinį tinkl¹ S_f1 (žr. 4 c) pav.), ir rast¹jį pseudomaksimalų sraut¹ perkeliame į tinkl¹ G_f1. Gauname sraut¹ (tinkl¹ G_f2).

Paskutinėje fazėje konstruojame pagalbinį tinkl¹ S_f2 (žr. 4 d) pav.). Kai šio tinklo pseudomaksimalų sraut¹ perkeliame į G_f2, gauname sraut¹ f, pavaizduot¹ 4 a) pav., kuris yra maksimalus tinklo G srautas, kadangi (žr. 1 paragrafo Fordo ir Falkersono teorem¹).

4 c) pav. gerai iliustruoja t¹ fakt¹, kad pseudomaksomalus srautas nebūtinai yra maksimalus srautas. Iš tikro, šiame paveikslėlyje pavaizduot¹ pseaudomaksimalų sraut¹ galime padidinti panaudojź ilgio 5 didinanči¹j¹ grandinź:

Taip pat pažymėsime, kad tinklo S_f2 (žr. 4 d) pav.) lankas atsirado iš pagrindinio tinklo G dviejų priešpriešais nukreiptų lankų.

Aptarkime pagalbinio tinklo ir jo pseudomaksimalaus srauto apskaičiavimo algoritmus.

Pagalbinio tinklo S_f apaskaičiavimo algoritmas

Tarkime, kad pradinio tinklo grafas nusakytas gretimumo struktūromis ir , .

– tai aibė viršūnių, į kurias iš viršūnės v išeina lankai.

– tai aibė viršūnių, iš kurių į viršūnź v įeina lankai.

Lankų pralaidum¹ žymėsime masyvu , , o faktin¹jį sraut¹ f – masyvu , . Tokia pralaidumo bei srauto vaizdavimo struktūra atminties požiūriu nėra racionali, tačiau prie šios struktūros algoritmas tampa vaizdesnis.

Kintamieji, vaizduojantys pagalbinį tinkl¹ , yra analogiški pradinio tinklo kintamiesiems ir jie žymimi tais pačiais vardais, pridedant prie jų pradinź raidź S. Tuo būdu, SV žymi tinklo viršūnių aibź; ir , , žymi gretimumo struktūr¹; Sc ir Sf atitinkamai žymi lankų pralaidumus ir sraut¹. Masyvo d elementas , , žymi tinklo viršūnės v nuotolį nuo šaltinio s.

Kaip buvo minėta aukščiau, tinklas konstruojamas paieškos platyn iš viršūnės s tinkle metodu. Paieškos platyn procese aplankytos viršūnės v talpinamos į eilź. Kiekviena iš eilės paimta viršūnė u nagrinėjama du kartus: pirm¹ kart¹ – ieškomi iš jos išeinantys leistinieji suderintieji lankai ; antr¹ kart¹ – ieškomi leistinieji nesuderintieji lankai .

Jei tinkle vienu metu lankas yra suderintasis ir nesuderintasis leistinasis lankas, t.y. – leistinasis suderintasis lankas, o – leistinasis nesuderintasis lankas, tai į tinkl¹ įtraukto lanko pralaidumas yra lygus šių lankų pralaidumų srauto f atžvilgiu sumai.

procedure psa

begin

for u I V do

begin

d [u] := ¥

SN [u] :=Æ; SPN [u] := Æ

for v I V do Sc [u, v] := 0;

for v I V do Sf [u, v] := 0;

end

Eil Æ; SV := Æ; d [s] := 0;

Eilė s

while Eil ¹ Æ do

begin

u Eilė

SV := SV È

for v I N [u] do

if ( d [u] < d [v] £ d [t] ) and (f [u, v] < c [u, v] ) then

begin

if d [v] = ¥ then Eil v

d [v] := d [u] + 1;

SN [u] := SN [u] È

SPN [v] := SPN [v] È

Sc [u, v] := c [u, v] – f [u, v];

end

for v I PN [u] do

if ( d [u] < d [v] £ d [t] ) and (f [v, u] > 0 ) then

begin

if d [v] = ¥ then Eil v

d [v] := d [u] + 1;

if Sc [u, v] = 0 then

begin

SN [u] := SN [u] È

SPN [v] := SPN [v] È

end

Sc [u, v] := Sc [u, v] + f [v, u];

end

end

end

Tarkime, po procedūros psa įvykdymo . Jei , tai reiškia, kad paieškos platyn metu nuotakio viršūnė t nebuvo pasiekta. Vadinasi, tinkle nuo s iki t nėra didinančiosios grandinės. Tada, remiantis 2 paragrafo teorema, galime teigti, kad srautas f yra maksimalus.

Jei , tai trumpiausios didinančiosios grandinės iš s į t ilgis yra l. Be to, visų kelių nuo s iki t ilgiai tinkle yra lygūs l, ir jie žymi l ilgio didinančiasias grandines tinkle . Reikia pažymėti, kad, pasiekus nuotakį t, tampa lygus , ir viršūnės v, kurioms , procedūroje psa nenagrinėjamos, kadangi nei viena tokia viršūnė negali priklausyti l ilgio keliui, jungiančiam s ir t.

Nesunku įvertinti procedūros psa sudėtingum¹. Kiekviena viršūnė v į eilź talpinama ir šalinama ne daugiau kaip vien¹ kart¹. Kiekvienas viršūnei v incidentiškas lankas analizuojamas vien¹ kart¹, be to, analizės veiksmų skaičius apribotas konstanta. Vadinasi, bendras veiksmų skaičius be inicializacijos yra . Inicializacijos veiksmų skaičius yra . Tuo būdu, procedūros psa sudėtingumas yra .

Belieka aptarti tinklo pseudomaksimalaus srauto efektyvaus apskaičiavimo algoritm¹. Žemiau pateiktas Malchotros, Kumaro ir Mahešvario (Malhotra V.M., Kumar P.M., Makeshvari S.N. An algorithm for finding maximum flows in networks. Information Processing Lett. 1978, 7, s. 277 – 278) pseudomaksimalaus srauto apskaičiavimo algoritm¹, kurio sudėtingumas yra .

Tinklo S_f pseudomaksimalaus srauto apskaičiavimo procedūra maxpsa

Šio algoritmo aprašymui įveskime tinklo viršūnės potencialo s¹vok¹.

Apibrėžimas. Tinklo viršūnės v potencialas yra maksimalus srauto kiekis, kurį galima praleisti per viršūnź v. Viršūnės v potencialas apibrėžiamas formule

Žemiau pateikta maxpsa procedūra pirmiausia apskaičiuoja pagalbinio tinklo visų viršūnių potencialus ir nulinio potencialo viršūnes patalpina į stek¹ STEK. Aišku, kad nulinio potencialo viršūnes drauge su joms incidentiškais lankais galima pašalinti iš tinklo , ir šis pašalinimas neturės įtakos jokiam tinklo srautui. Tokių viršūnių, o tikslaiu joms incidentiškų lankų pašalinimas gali paveikti kitų tinklo viršūnių potencialus, ir jie gali tapti lygūs nuliui. Jei taip atsitinka, tai naujos nulinio potencialo viršūnės šalinamos iš tinklo.

Jei, pasibaigus nulinio potencialo viršūnių šalinimo procesui, tinklas neturi nenulinio potencialo viršūnių, tai tinklo pseudomaksimalus srautas surastas. Priešingu atveju randame mažiausio potencialo viršūnź r ir jos potencial¹ p. Tada iš viršūnės r į viršūnź t ir iš viršūnės s į viršūnź r konstruojame p dydžio sraut¹. Tuo būdu apskaičiuojamas p dydžio srautas iš šaltinio s į nuotakį t. Šis srautas naudos tik leistinuosius suderintuosius lankus.

Aptarsime, kaip konstruojamas p dydžio srautas iš viršūnės r į viršūnź t. Srauto iš viršūnės s į viršūnź r konstravimas yra analogiškas.

Kaip buvo minėta, p dydžio srautas iš viršūnės r į viršūnź t naudos tik suderintuosius leistinuosius lankus, ir jį patogiausia konstruoti naudojant paiešk¹ platyn iš viršūnės r. Įsivaizduokime, kad viršūnėje r patalpintas krovinys , ir mes norime “perkelti” šį krovinį į viršūnź t. Kiekviena paieškos platyn metu aplankyta viršūnė v “perkelia” krovinį į viršūnes u, į kurias eina lankai iš viršūnės v. Be to, į viršūnź u “perkeliamo” krovinio dalis yra lygi lanko pralaidumui, t.y. . Aišku, kad tokie lankai gali būti šalinami iš tinklo. Lankų šalinimas iššaukia viršūnių potencialų perskaičiavim¹, ir, jei viršūnės v potencialas tampa lygus nuliui, tai viršūnė v talpinama į stek¹ STEK.

Tuo būdu, krovinys iš viršūnės r, kuri nuo šaltinio s nutolusi atstumu d, pirmiausia bus “perkeltas” į viršūnes, nutolusias nuo šaltinio s atstumu , po to, iš šių viršūnių, į viršūnes, nutolusias nuo šaltinio s atstumu ir t.t. iki visas krovinys bus “perkeltas” į viršūnź t. Kadangi p yra mažiausias viršūnės potencialas, tai toks krovinio “perkėlimas” visada yra galimas.

Kaip minėjome, srautas iš s į r konstruojamas analogiškai.

p dydžio srauto iš viršūnės s į t konstravimu baigiasi pagrindinio ciklo veiksmai, ir, kaip buvo minėta aukščiau, pagrindinis ciklas bus kartojamas, kol tinklas turės nenulinio potencialo viršūnių.

procedure maxpsa

begin

STEK Æ

for v I SV do

begin

Pin [v] := 0; Pout [v] := 0;

if v = s then Pin [v] := ¥

else

for uI SPN [v] do

Pin [v] := Pin [v] +Sc [u, v];

if v = t then Pout [v] := ¥

else

for uI SN [v] do

Pout [v] := Pout [v] + Sc [v, u];

P [v] := min (Pin [v], Pout [v]);

if P [v] = 0 then STEK v

end

for v I SV do Q [v] := 0;

XN := SV;

while XN ¹ Æ do

begin

while STEK ¹ Æ do

begin

v STEK; XN := XN

for u I SPN [v] do

begin

Pout [u] := Pout [u] – (Sc [u, v] – Sf [u, v]);

SN [u] := SN [u] ;

SPN [v] := SPN [v] ;

if P [u] ¹ 0 then

begin

P [u] := min (Pin [u], Pout [u]);

if P [u] = 0 then STEK u

end

end

for u I SN [v] do

begin

Pin [u] := Pin [u] – (Sc [v, u] –Sf [v, u]);

SPN [u] := SPN [u] ;

SN [v] := SN [v] ;

if P [u] ¹ 0 then

begin

P [u] := min (Pin [u], Pout [u]);

if P [u] = 0 then STEK u

end

end

end

if XN ¹ Æ then

begin

p ¥

for v I XN do

if P [v] < p then

begin

r :=v;

p := P [r];

end

Eilė Æ Eilė r; Q [r] := p;

repeat

v Eilė

Pin [v] := Pin [v] – Q [v];

Pout [v] := Pout [v] – Q [v];

P [v] := P [v] – Q [v];

if P [v] = 0 then STEK v

if v = t then Q [v] := p

else

begin

u := pirmoji aibės SN [v] viršūnė

while Q [v] > 0 do

begin

if Q [u]  = 0 then Eilė u

delta := min (Q [v], Sc [v, u] – Sf [v, u]);

Sf [v, u] := Sf [v, u] + delta;

Q [v] := Q [v] – delta;

Q [u] := Q [u] + delta;

if Sf [v, u] = Sc [v, u] then

begin

SN [v] := SN [v] ;

SPN [u] := SPN [u] ;

end

if Q [v] > 0 then

u := po viršūnės u einanti kita aibės SN [v] viršūnė

end

end

until v = t;

Eilė Æ Eilė r; Q [r] := p;

repeat

v Eilė

if v ¹ r then

begin

Pin [v] := Pin [v] – Q [v];

Pout [v] := Pout [v] – Q [v];

P [v] := P [v] – Q [v];

if P [v] = 0 then STEK v

end

if v = s then Q [v] := 0

else

begin

u := pirmoji aibės SPN [v] viršūnė

while Q [v] > 0 do

begin

if Q [u] = 0 then Eilė u

delta := min (Q [v], Sc [u, v] – Sf [u, v]);

Sf [u, v] := Sf [u, v] + delta;

Q [v] := Q [v] – delta;

Q [u] := Q [u] + delta;

if Sf [u, v] = Sc [u, v] then

begin

SPN [v] := SPN [v] ;

SN [u] := SN [u] ;

end

if Q [v] > 0 then

u := po viršūnės u einanti kita aibės
SPN [v] viršūnė

end

end

until v = s;

end

end

end

Aptarkime procedūros maxpsa sudėtingum¹. Pradinis viršūnių potencialų apskaičiavimas reikalauja veiksmų, kadangi kiekvienas grafo lankas analizuojamas ne daugiau kaip du kartus: apskaičiuojant Pout [v] ir Pin [v].

Pagrindinio ciklo nulinio potencialo viršūnių šalinimo sudėtingumas taip pat yra , kadangi kiekviena viršūnė į stek¹ STEK talpinama vien¹ kart¹, o šalinant viršūnź iš steko pašalinamos visos jai incidentiškos briaunos, tuo būdu kiekvienas lankas šalinamas ne daugiau kaip vien¹ kart¹.

Kiekviena pagrindinio ciklo iteracija iššaukia ne mažiau kaip vienos nulinio potencialo viršūnės atsiradim¹ (viršūnės r potencialas visada bus lygus nuliui). Vadinasi, pagrindinio ciklo pasikartojimų skaičius neviršija n.

Pagrindiniame cikle, be minėtų nulinio potencialo viršūnių šalinimo veiksmų, naudojant paiešk¹ platyn konstruojamas p dydžio srautas iš r į t ir iš s į r. Šių dalių sudėtingumas yra lygus lankų analizavimo skaičiaus eilei.

Lanko analizė gali būti “naikinamoji”, kai srautas per lank¹ yra lygus to lanko pralaidumui, ir toks lankas šalinamas iš tinklo.

Lanko analizė gali būti “nenaikinamoji”, kai srauto per lank¹ dydis yra mažesnis už to lanko pralaidum¹. Toks lankas iš tinklo nešalinamas ir gali būti analizuojamas kartojant pagrindinį cikl¹.

Aišku, kad per visus pagrindinio ciklo pasikartojimus “naikinamuoju” būdu analizuojame lankų, o kiekviename pagrindiniame cikle “nenaikinamuoju” būdu analizuojame ne daugiau kaip n lankų (po vien¹ kiekvienai aplankytai viršūnei). Vadinasi, per visus pagrindinio ciklo pasikartojimus “nenaikinamuoju” būdu bus analizuota ne daugiau kaip n² lankų. Tuo būdu, bendras pagrindinio ciklo veiksmų skaičius yra , t.y. .

Iš viso nagrinėjimo darome išvad¹, kad procedūros maxpsa sudėtingumas yra .

Dabar aprašytas psa ir maxpsa procedūras galima sukomponuoti į vien¹ bendr¹ maksimalaus srauto apskaičiavimo algoritm¹.

Maksimalaus srauto apskaičiavimo algoritmas

Duota: tinklas, nusakytas gretimumo struktūromis ir , ; laukų pralaidumu , ; šaltiniu s ir nuotakiu t.

Rezultatas:  maksimalus srautas , .

begin

for u I V do

for v I V do f [u, v] :=0; .

repeat

psa

if d [t] ¹ ¥ then

begin

maxpsa

for u I SV do

for v I SV do

begin

f [u, v] := f [u, v] + Sf [u, v];

if f [u, v] > c [u, v] then

begin

f [v, u] := f [v, u] – (f [u, v] – c [u, v]);

f [u, v] := c [u, v];

end

end

end

until d [t] = ¥

end

Išvada. Iš procedūrų psa ir maxpsa sudėtingumo analizės bei to, kad fazių skaičius neviršija išplaukia, kad pateikto maksimalaus srauto algoritmo sudėtingumas yra . Tuo pačiu šių algoritmų analizė parodė, kad bet kokiam tinklui egzistuoja maksimaus srautas. O tai ir yra Fordo ir Falkersono teoremos pilno įrodymo trūkstama grandis.

Šį paragraf¹ baigsime akivaizdžia, bet svarbia pateikta maksimalaus srauto radimo algoritmo savybe.

Teorema. Jeigu tinklo visų lankų pralaidumai yra sveikieji skaičiai, tai maksimalus srautas, apskaičiuotas pagal pateikt¹ algoritm¹, yra sveikaskaitinis, t.y. yra sveikasis skaičius kiekvienam tinklo lankui .

Maksimalaus suporavimo uždavinys dvidaliame grafe

Apibrėžimas. Suporavimas neorientuotajame grafe – tai toks grafo G briaunų poaibis , kad bet kokios dvi poaibio M briaunos tarpusavyje nėra gretimos, t.y. bet kokios dvi poaibio M briaunos nėra incidentiškos vienai ir tai pačiai viršūnei.

Jei briauna , tai sakome, kad M suporuoja u ir v viršūnes.

Jei viršūnė v nėra incidentiška nei vienai poaibio M briaunai, tai viršūnė v vadinama laisv¹ja viršūne, priešingu atveju – suporuot¹ja.

Maksimalaus suporavimo neorientuotame grafe uždavinys yra plačiai paplitźs, ir yra žinomi efektyvūs šio uždavinio sprendimo algoritmai. Visi jie pagrįsti alternuojančių grandinių teorija (teorija čeredujuščichsia cepei).

Tarkim, M – grafo G suporavimas.

Apibrėžimas. Grafo G grandinė, kuri¹ sudaro biaunos, pakaitomis nepriklausančios ir priklausančios poaibiui M, vadinama suporavimo M atžvilgiu alternuojančia grandine.

Grandinė, kurios ilgis lygus 1, pagal apibrėžim¹ taip pat yra alternuojanti.

Alternuojančios grandinės briaunos, priklausančios suporavimui M, vadinamos tamsiomis briaunomis, o nepriklausančios M – šviesiomis briaunomis.

Pavyzdys. Panagrinėkime 5 pav. pavaizduot¹ graf¹.

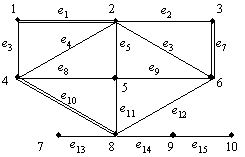
5 pav. Suporavimo uždavinys

Aibė yra suporavimas grafe G; grandinė yra suporavimo M atžvilgiu alternuojanti grandinė; , – tamsiosios grandinės P briaunos; , , – šviesiosios grandinės P briaunos; aibės ir – atitinkamai suporuotųjų ir laisvųjų viršūnių aibės.

Aišku, kag jei grafe G suporavimo M atžvilgiu egzistuoja grandinė, jungianti dvi laisv¹sias viršūnes, tai grafe G galima sukonstruoti suporavim¹, turintį didesnį briaunų skaičių nei M. Aišku, kad tokios alternuojančios grandinės šviesiųjų briaunų skaičius yra vienetu didesnis nei tamsiųjų. Pašalinź iš M visas tamsiasias grandinės briaunas, ir į M įvedź visas šviesiasias tos grandinės briaunas, gausime suporavim¹, kuriame briaunų skaičius bus vienetu didesnis nei M. Dėl tos priežasties alternuojanti grandinė, jungianti dvi laisvasias viršūnes, vadinama didinančiaja grandine.

Teorema (K.Beržas). Neorientuotojo grafo G suporavimas M yra didžiausias tada ir tiktai tada, kai šiame grafe suporavimo M atžvilgiu nėra didinančiosios grandinės.

Šiai teoremai iliustruoti panagrinėkime aukščiau 5 pav. pateikt¹ graf¹. Imkime suporavim¹ ir didinanči¹j¹ grandinź . Dabar galima sudaryti didesnį suporavim¹ .

Suporavimas taip pat nėra didžiausias, nes šio suporavimo atžvilgiu egzistuoja grandinė .

Gausime suporavim¹ , kuris yra didžiausias, nes jo atžvilgiu grafe nėra didinančiosios grandinės.

Tuo būdu, Beržo teorema nusako toki¹ didžiausio suporavimo radimo strategij¹.

Randame bet kokį pradinį suporavim¹ M.

Pavyzdžiui, pradinis suporavimas gali būti būti kuri grafo briauna.

Didesnio pradinio suporavimo galima ieškoti, naudojant “godaus” algoritmo strategij¹:

a)    rasti briaun¹, kurios incidentiškų viršūnių laipsnių suma yra mažiausia, ir įtraukti ši¹ briaun¹ į suporavim¹;

b)   iš grafo pašalinti į suporavim¹ įtraukt¹ briaun¹ drauge su jai gretimomis briaunomis.

Aišku, kad punktai a) ir b) bus kartojami tol, kol grafas G turės bent vien¹ briaun¹.

Nuosekliai konstruoti suporavimų sek¹ , kurioje gaunamas iš radus grafe G suporavimo atžvilgiu didinanči¹j¹ grandinź. Kadangi , tai sekos ilgis bus nedidesnis nei . Todėl norint rasti efektyvų šio uždavinio sprendimo algoritm¹, pagrįst¹ išnagrinėta strategija, reikia sukonstruoti efektyvų didinančiosios grandinės radimo algoritm¹. Nors tokie efektyvūs algoritmai egzistuoja, čia apsiribosime didžiausio suporavimo dvidaliame grafe nagrinėjimu.

Dažniausiai suporavimo uždavinys sprendžiamas dvidaliuose grafuose (žr. 2.2, 2.10 paragrafus). Tai klasikinis kombinatorikos uždavinys, žinomas “uždavinio apie sutuoktinių poras” vardu.

Primename, kad -grafas yra dvidalis, jei jo viršūnių aibź V galima išskaidyti į du poaibius X ir Y taip, kad visų grafo G briaunų galai priklausytų skirtingiems poaibiams. Todėl dvidalis grafas žymimas .

“Uždavinys apie sutuoktinių poras” turi toki¹ interpretacij¹. Tarkime, X ir Y atitinkamai yra vaikinų ir merginų aibės. Sudarykime dvidalį graf¹ , čia , jei jaunuolis x draugauja su mergaite y. Tada kiekvienas suporavimas M atitinka aibź galimų sutuoktinių porų, kiekviena iš kurių sudaryta iš tarpusavyje draugaujančių jaunuolio ir merginos; be to, kiekvienas žmogus dalyvauja ne daugiau kaip vienoje poroje.

Pasirodo, kad maksimalaus suporavimo uždavinį dvidaliame grafe galima lengvai suvesti į maksimalaus srauto tinkle ieškojimo uždavinį.

Tarkime, – dvidalis grafas. Sudarykime tinkl¹ , kuris turėtų šaltinį s, nuotakį t ( ir ), viršūnių aibź , lankų aibź

ir kiekvieno lanko pralaidumas .

Pavyzdys. 6 a) pav. pavaizduotas dvidalis grafas H, o 6 b) pav. – jam atitinkantis tinklas .

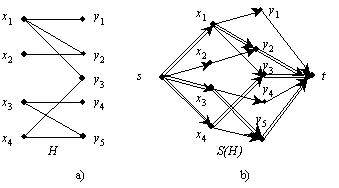
6 pav. Dvidalis grafas H ir jam atitinkantis tinklas S(H). Suporavimas
M = ir jam atitinkantis srautas f_M.

Teorema. Kiekvienam grafo H k galios suporavimui , (, visiems ) egzistuoja vienintelis tinklo dydžio k sveikaskaitinis srautas apibrėžiamas taip:

visiems ,

visiems likusiems tinklo lankams e;

ir atvirkščiai, kiekvienam tinklo dydžio k srautui f atitinka vienintelis grafo H suporavimas , apibrėžiamas taip:

6 pav. pavaizduotas suporavimas grafe H ir jam atitinkantis srautas tinkle .

Ši teorema įgalina maksimalaus srauto apskaičiavimo algoritmus, išnagrinėtus 6 paragrafe, panaudoti apskaičiuojant maksimalų suporavim¹ dvidaliame grafe.

Naudodami Dinico metod¹, maksimalų suporavim¹ galima apskaičiuoti atlikus veiksmų. Tačiau, atsižvelgiant į tinklo specifik¹, yra sukurti efektyvesni maksimalaus suporavimo apskaičiavimo algoritmai. Čia panagrinėsime Hopkrofto ir Karpo algoritm¹, kurio sudėtingumas yra (žr. Hopcroft J., Karp R.M. An algorithm for maximum Matchings in bipartite graphs. SIAM J. Comput., 1973, 2, s. 225-231).

Šis algoritmas naudoja bendr¹ Dinico metodo schem¹. Vienok, dėl tinklo specifikos galima sumažinti tiek fazių skaičių, tiek ir sukurti efektyvesnį pseudomaksimalaus srauto kiekvienoje fazėje apskaičiavimo algoritm¹.

Pirmiausia pašymėsime, kad tinklo kiekvienos didinančiosios grandinės ilgis yra nelyginis skaičius, ir, iš jos atmetus pirm¹j¹ ir paskutini¹j¹ grandis, ši grandinė bus alternuojanti, prasidedanti ir pasibaigianti šviesiaja briauna (leistinaisiais suderintaisiais lankais).

Apibrėžimas. Duotajam suporavimui M ilgio , iš X į Y grandinź :

kurioje visos viršūnės yra skirtingos, x₀ – laisvoji X aibės viršūnė, o y_k+1 – laisvoji Y aibės viršūnė, o kiekviena antroji briauna priklauso M, t.y.

vadinsime alternuojančia grafo H grandine.

Aišku, kad alternuojanči¹ grandinź galima nusakyti viršūnių seka. Ši seka vieninteliu būdu apibrėžia srauto atžvilgiu didinanči¹j¹ grandinź:

Be to, šios grandinės iššauktas srauto padidėjimas nusako suporavim¹, gaut¹ susumavus aibes A ir P moduliu 2: .

Pavyzdžiui, 7 a) pav. pavaizduotas dvidalis grafas ir suporavimas M; 7 b) pav. pavaizduota didinančioji alternuojančioji grandinėP, o 7 c) pav. pavaizduotas suporavimas .

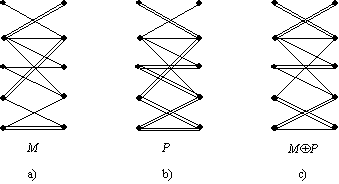
7 pav. Suporavimo M padidinimas, panaudojant alternuojanči¹ grandinź P

Aišku, kad ir dvidalio grafo H atveju yra teisinga Beržo teorema: grafo H suporavimas M yra didžiausias tada ir tiktai tada, kai šiame grafe suporavimo M atžvilgiu nėra didinančiosios grandinės.

Aprašysime Hopkrofto ir Karpo algoritm¹. Šio algoritmo schema yra analogiška Dinico algoritmo schemai: kiekvienoje fazėje tinklui apskaičiuosime pagalbinį bekontūrinį tinkl¹, jo pseudomaksimalų sraut¹ ir jį “perkelsime” į pagrindinį tinkl¹. Kaip buvo minėta aukščiau, dėl tinklo specifikos šie algoritmai yra efektyvesni nei Dinico metode naudojamas analogiškas algoritmas, o fazių skaičius – mažesnis.

Pirmiausia aptarsime pagalbinio bekontūrinio tinklo apskaičiavimo algoritm¹ PGA.

Tarkime, yra dvidalis grafas, o M – suporavimas šiame grafe. Graf¹ H pakeiskime orientuotuoju grafu tokiu būdu: kiekvienai suporavimo M briaunai suteikime orientacij¹ nuo Y į X, o visoms likusioms briaunoms – orientacij¹ nuo X į Y. Aišku, kad tada kelias nuo laisvosios viršūnės į laisv¹j¹ viršūnź bus srauto M atžvilgiu didinančioji grandinė.

Procedūra PGA pradžioje konstruoja bekontūrinio tinklo lankus nuo viršūnės s į visas laisv¹sias aibės X viršūnes. Po to iš šių laisvųjų viršūnių grafe organizuojama paieška platyn. Jei paieškos platyn metu pasiekiame laisv¹j¹ viršūnź , tai į bekontūrinį tinkl¹ įtraukiame lank¹ . Be to, nuo to momento, kai į tinkl¹ įtraukiamas pirmasis toks lankas, daugiau nenagrinėjamos viršūnės, kurios nutolź nuo viršūnės s nemažiau kaip kelio nuo s iki t ilgis.

Panagrinėkime pseudomaksimalų sraut¹ procedūros PGA sukonstruotame pagalbiniame tinkle. Šiame pagalbiniame ilgio tinkle l ilgio (atmetame 1-¹jį ir paskutinįjį lankus) alternuojančios didinančiosios grandinės visų viršūnių potencialai yra lygūs 1. Pagal ši¹ grandinź padidinus sraut¹, visos grandinės viršūnės eliminuojamos iš tolesnio nagrinėjimo. Vadinasi, pagalbinio tinklo pseudomaksimalų sraut¹ apibrėš didžiausia aibė ilgio l poromis nesusikertančių alternuojančių grandinių. Tokių grandinių ieškojim¹ realizuoja procedūra fazė, kuri naudoja paieškos gilyn iš viršūnės s pagalbiniame tinkle metod¹. Naujos aplankytos viršūnės talpinamos į stek¹ STEK. Kiekvien¹ kart¹, kai pasiekiama viršūnė t, steke esančios viršūnės apibrėžia alternuojanči¹ didinanči¹j¹ grandinź. Tada visos viršūnės, išskyrus viršūnź s, šalinamos iš steko kartu didinant sraut¹ (suporavim¹), kurį nusako masyvas pora. Žemiau pateikti procedūrų PGA, fazė ir pagrindinės programos tekstai.

Hopkrofto ir Karpo didžiausio suporavimo algoritmas

Duota:  Dvidalis grafas , nusakytas gretimumo struktūra , čia – aibė viršūnių, gretimų viršūnei x.

Rasti:  Didžiausi¹ suporavim¹, kurį nusako masyvas pora [1..n], , kurios elementas

procedure PGA

begin

for u I V È do

begin

d [u] = ¥

SN [u] := Æ

end

Eilė Æ; SV := Æ

SV := SV È

d [s] := 0;

for x I X do

if pora [x] = 0  then

begin

Eilė x

SN [s] := SN [s] È

d [x] := 1;

end

while Eilė ¹ Æ do

begin

u Eilė

SV := SV È

if u I Y then

if pora [u] = 0 then

begin

SN [u] := SN [u] È t

if d [t] = ¥ then

begin

SV := SV È

d [t] := d [u] + 1;

end

end

else

begin

x := pora [u];

if d [t] = ¥ then

begin

Eilė x

SN [u] := SN [u] È

d [x] := d [u] + 1;

end

end

else

for y I N [u] do

if d [u] < d [y] then

begin

if d [y] = ¥ then Eilė y

SN [u] := SN [u] È

d [y] := d [u] + 1;

end

end

end

procedure faz

begin

for u I SV do

begin

naujas [u] := true;

p [u] := pradžia [u];

end

STEK Æ; STEK s; naujas [s] := false;

while STEK ¹ Æ do

begin

u := top (STEK);

if p [u] = nil then b := false

else b := not naujas [p [u] .viršūnė

while b do

begin

p [u] := p [u] pėdsakas

if p [u] = nil then b := false

else b := not naujas [p [u] .viršūnė

end

if p [u] ¹ nil then

if p [u] .viršūnė = t then

while top (STEK) ¹ s do

begin

y STEK

x STEK

pora [x] := y; pora [y] := x;

end

else

begin

v := p [u] .viršūnė

STEK v

naujas [v] := false;

end

else

u STEK

end

end

begin

for v I V do pora [v] := 0;

PGA

while t I SV do

begin

fazė

PGA

end

end

Reikia pažymėti, kad didelis Hopkrofto ir Karpo algoritmo efektyvumas gaunamas todėl, kad fazių skaičius yra nedidesnis nei [Lip88].