Kombinatorinių objektų generavimo algoritmai

Kombinatorinių objektų generavimo algoritmai

Šiame paragrafe aptarsime pagrindinius kombinatorinių objektų (derinių, kėlinių, aibės išskaidymo ir kt.) generavimo algoritmus.

Optimali tokių objektų generavimo algoritmo struktūra yra:

begin

generuoti pradinį junginį (kombinatorinį objekt¹);

while “generavimo s¹lyga” do

begin

nagrinėti (spausdinti) junginį (kombinatorinį objekt¹);

generuoti junginį (kombinatorinį objekt¹), gretim¹ išnagrinėtam (atspausdintam).

end

end

Priklausomai nuo pasirinktų objektų bei jų generavimo tvarkos, šiame algoritme turi būti konkretizuoti sakiniai “generuoti pradinį junginį”, “generavimo s¹lyga”, “generuoti gretim¹ junginį”.

Derinių generavimo algoritmai

Derinių generavimas leksikografine tvarka

Pirmiausia aptersime derinių generavimo leksikografine didėjimo tvarka algoritm¹. Apie leksikografinź vektorių tvark¹ kalbėjome 1.3 paragrafe. Čia priminsime, kad jei į derinį žiūrėsime kaip į skaičių, tai deriniams atitinkantys skaičiai bus išdėstyti didėjimo tvarka.

Pavyzdys. Panagrinėkime . Deriniai, surašyti leksikografine tvarka, bus:

Derinius nuosekliai talpinsime masyve ir šio masyvo elementai apibrėš derinį.

Pradinio derinio generavimas. Aišku, kad pradinis derinys generuojamas taip:

for l 0 to k do c [l] := l;

Kaip generuoti patį mažiausi¹ leksikografiškai didesnį derinį nei turimas?

Tarkime, – turimas derinys. Leksikografine tvarka pats didžiausias derinys yra: . Vadinasi, , . todėl, norint apskaičiuoti patį mažiausi¹ leksikografiškai didesnį derinį nei nagrinėjamas derinys, elgsimės taip:

masyve rasime pirm¹ iš dešinės element¹ c_l, , tenkinantį s¹lyg¹ ;

šį element¹ padidinsime vienetu, t.y. ;

likusius elementus užpildysime iš eilės einančiais natūraliaisiais skaičiais, t.y.

for i l + 1 to k do c_i: = c_i-1 + 1;

Generavimo pabaigos s¹lyga. Jei pirmasis iš dešinės elementas, tenkinantis s¹lyg¹ , yra , tai reiškia, kad nagrinėjame derinį: . Vadinasi, jau visi deriniai sugeneruoti.

Tuo būdu, derinių generavimo leksikografine tvarka algoritmas yra.

Derinių skaičiaus apskaičiavimo algoritmas

Duota:  n – objektų skaičius,

k – objektų skaičius derinyje.

Rasti:  generuoti derinius leksikografine tvarka.

begin

for l := 0 to k do c [l] := l;

p := true;

while p do

begin

spausdinti derinį

l := k;

while (l >= 1) and c [l] >= n – k + l do l := l – 1;

if l = 0 then p := false

else begin

c [l] := c [l] + 1;

for i := l + 1 to k do c [i] := c [i – 1] + 1;

end

end

end

Trečiasis Grėjaus kodų generavimo algoritmas

Kaip matyti iš antrojo Grėjaus kodo generavimo algoritmo (žr. 1.3 paragraf¹), Grėjaus kodus galima generuoti iš pradinio kodo, žinant sek¹ . Šios sekos elementas žymi skiltį, kuri¹ reikia invertuoti, kad iš -ojo kodo gautume i-¹jį kod¹.

Pavyzdžiui, kai , seka T₃ yra tokia: .

Vadinasi, pakanka mokėti efektyviai generuoti sek¹ T_n, kad galėtume generuoti Grėjaus kodus.

Sek¹ T_n galima efektyviai generuoti naudojant stek¹.

Pradžioje stekas užpildomas elementais: (viršuje yra elementas 1). Algoritmas ima viršutinį steko element¹ i ir patalpina jį į sek¹ T_n; po to į stek¹ įrašomi elementai . Būtent tokiu būdu žemiau pateiktas algoritmas generuoja Grėjaus kodus.

begin

s

for j := n downto 1 do begin

g [j] := 0;

s j

end

while s ¹ Æ do

begin

spausdinti

i s

g [i] := 1 – g [i];

for j := i – 1 downto 1 do s j

end

end

end

Skaičiuojant pagal šį algoritm¹, steko turinys (viršutinis elementas yra steko viršūnėje) kis taip: 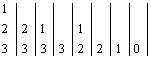, o i reikšmės sudarys T₃ sek¹ .

Pateikt¹ algoritm¹ galima patobulinti. Kiekvien¹ kart¹, kai į stek¹ patalpinamas elementas , mes apriori žinome, kad virš jo bus patalpinti elementai . Protingas šios informacijos panaudojimas įgalina vietoj steko naudoti masyv¹ tokiu būdu. Elementas yra viršutinis steko elementas ir kiekvienam yra elementas, steke esantis tuoj po elemento j (žemiau elemento j), jei j yra steke. Jei elemento j steke nėra, tai elemento reikšmė negali turėti jokios įtakos skaičiavimams ir todėl priskiriame reikšmź , kadangi mes žinome, kad kai kit¹ kart¹ elementas bus patalpintas į stek¹, elementu, esančiu virš jo, bus elementas j. Dar daugiau, kadangi elementai bus talpinami į stek¹ pašalinus element¹ i, mums reikia tiktai priskirti , laikant, kad visiems j, , reikšmė buvo priskirta, kai j buvo pašalintas iš steko (primename, tada ). Pagaliau, kai , elementai į stek¹ patalpinami operacijos dėka.

Dabar gausime tokį algoritm¹.

begin

for j := 0 to n + 1 do begin

g [j] := 0;

t [j] := j + 1;

end

i

while i < n + 1 do

begin

spausdinti

i t

g [i] := 1 – g [i];

t [i – 1] := t [i];

t [i] := i + 1;

if i ¹ 1 then t

end

end

Kai , masyvo t turinys skaičiavimo eigoje kis taip:

Pateikt¹jį algoritm¹ galima truputį patobulinti. Pastebėsim, jei operatorių patalpintume po operatoriaus g [i] := 1 – g [i], tai operatorių if i ¹ 1 then t[0]:=1 galima išmesti. Iš tikro, jei , tai operatorius
t [i – 1] := t [i] tuoj pat ištaisys neteising¹ t [0] reikšmź. Tuo būdu galutinis Grėjaus kodų generavimo algoritmas bus toks.

begin

for j := 0 to n + 1 do begin

g [j] := 0;

t [j] := j + 1;

end

i

while i < n + 1 do

begin

spausdinti

i t

g [i] := 1 – g [i];

t t [i – 1] := t [i]; t [i] := i + 1;

end

end

Derinių generavimas minimalaus pokyčio tvarka

Aptarkome derinių generavimo minimlaus pokyčio tvarka algoritm¹. Minimlaus pokyčio tvarka – tai tokia derinių seka, kai bet koks šios sekos derinys yra gaunamas iš prieš jį stovinčio derinio, pakeitus jame vien¹ element¹ kitu.

Pavyzdys. Panagrinėkime . Deriniai, surašyti minimalaus pokyčio tvarka, bus tokie:

Nesunku pastebėti, kad bet koks šios sekos derinys, išskyrus pirm¹jį, yra gaunamas iš prieš jį stovinčio derinio, pakeitus vien¹ element¹ kitu.

Jei pirmajame derinyje element¹ 2 pakeisime elementu 4, tai gausime antr¹jį derinį. Jei jame element¹ 1 pakeisime elementu 2, tai gausime treči¹jį derinį ir t.t.

Reikia pastebėti, kad ši derinių seka yra užciklinta, t.y. jei paskutiniame derinyje element¹ 5 pakeisime elementu 3, tai gausime pirm¹jį šios sekos derinį.

Kiekvien¹ derinį galima užkoduoti n-skilčiu dvejetainiu skaičiumi : jei , tai elementas i priklauso deriniui; jei , tai elementas i nepriklauso deriniui. Tuo būdu deriniai bus užkoduoti n-skilčiais dvejetainiais skaičiais, kiekvienas iš kurių turi k vienetukų ir nulių.

Aišku, kad minimalaus pokyčio derinių sekos kodai bus dvejetainiai skaičiai, turintys k vienetukų, ir bet kokie du gretimi skaičiai skirsis dviem skiltimis: vienoje nulis keičiamas vienetu, o kitoje vienetas keičiamas nuliu.

Pavyzdys. Aukščiau pateikto minimalaus pokyčio derinių sekos kodai bus:

Tokių kodų generavimas yra glaudžiai susijźs su 1.3 paragrafe išnagrinėtu Grėjaus kodų generavimu.

Tarkime, – Grėjaus kodai, o , – seka Grėjaus kodų, turinčių lygiai k vienetukų. Tada, kaip parodyta literatūroje [RND80], seka sutampa su minimalaus pokyčio derinių seka.

Pavyzdys. Panagrinėkime Grėjaus kodus, kai . Remiantis 1.3 paragrafe išnagrinėtu algoritmu, gausime toki¹ sek¹:

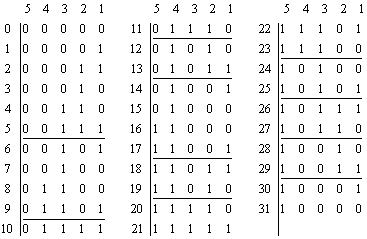
Kodai, turintys 3 vienetukus, – pabraukti. Išrašź šiuos kodus, gausime minimalaus pokyčio derinio sekos kodus.

Norėdami efektyviai generuoti , , kodus, pasinaudokime rekursyviniu apibrėžimu:

(3.4.1)

ir

čia žymi kodus, surašytus atvirkščia tvarka, o reiškia, kad n skilčių užpildome nuliais, o – kad n skilčių užpildome vienetais.

Pastaroji rekurentinė formulė generuoja pradedant ir baigiant.

Pavyzdys. Remdamiesi (3.4.1) formule, pavaizduokime generavimo medį (žr. 3.4.1 pav.).

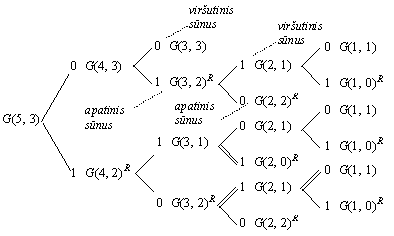
1 pav. G(5, 3) generavimas, remiantis (3.4.1) rekurentine formule

Remdamiesi šiuo medžiu, gausime sek¹:

Nesunku parodyti (žr. [RND80]), kad 3.4.1 pav. pavaizduoto binarinio medžio kabančios viršūnės yra arba arba .

Kodų generavimo uždavinys transformuojasi į binarinio medžio kabančių viršūnių peržiūr¹: pradedant viršutine ir baigiant apatine.

Norint pereiti nuo vienos kabančios viršūnės į gretim¹ kabanči¹ viršūnź, nagrinėjame keli¹ iš pirmos kabančios viršūnės medžio šaknies link. Tuo keliu link šaknies keliaujame viršūnėmis, kurios yra apatiniai sūnūs (žr. 3.4.1 pav.). Pasiekź pirm¹j¹ viršūnź, kuri yra viršutinis sūnus, pereiname pas jo brolį (apatinį sūnų) ir iš jo, eidami viršutiniais sūnumis, einame į kabanči¹ viršūnź.

Pavyzdžiui (žr. 3.4.1 pav.), išnagrinėjź kabanči¹ viršūnź , pirmiausia pasieksime viršutinį sūnų ir pereisime pas jo brolį (apatinį sūnų) . Ir iš jo viršutiniais sūnumis , pasieksime viršūnei gretim¹ kabanči¹ viršūnź . (3.4.1 pav. šis kelias paryškintas).

Nagrinėdami kabanči¹ binarinio medžio viršūnź , mes tuo pačiu žinome keli¹ iš šaknies į kabanči¹ viršūnź. Norėdami pereiti prie gretimos kabančios viršūnės, turime saugoti informacij¹ apie viršūnź , į kuri¹ turime sugrįžti (viršūnės visada yra apatiniai sūnūs). Šios viršūnės bus saugomos steke. Toliau pateiktame generavimo algoritme stekas bus organizuojamas taip pat, kaip jis buvo organizuotas generuojant Grėjaus kodus (žr. treči¹jį Grėjaus kodų generavimo algoritm¹). Parametras t rodo skaičių vienetukų tarp skilčių ir gali būti nesunkiai apskaičiuojamas. Todėl steke saugoma tik i reikšmė.

Atidžiai ištyrinėjus binarinį medį, galima pastebėti, kad nagrinėjamo kodo, kai iš jo grįžtama į viršūnź , perskaičiavimas į gretim¹ kod¹ reiklauja nagrinėti žemiau pateiktus keturis atvejus, priklausomai nuo g_i ir t reikšmės:

Šie pertvarkymai turi įtakos vienetukų skaičiui tarp skilčių : t reikšmź turime sumažinti 1, jei , ir padidinti 1, jei .

Pereinant prie gretimo kodo yra invertuojamos dvi skiltys:

skiltis ,

ir

Atlikus šiuos veiksmus, į stek¹ reikia įrašyti papildom¹ informacij¹: tarpines viršūnes, esančias tarp nagrinėjamos viršūnės ir nagrinėjamos kabančios viršūnės. Kadangi tas priklauso nuo viršūnės steko viršuje, tai t reikšmė gali vėl pasikeisti.

Jei arba , tai reiškia, kad viršūnė, kurioje mes esame, yra kabanti viršūnė: arba ir jokių tarpinių viršūnių saugoti nereikia. Šiuo atveju t visada lygus .

Kita vertus, jei ir , tai į stek¹ turime įtraukti viršūnes , išskyrus t¹ atvejį, kai . Šiuo atveju į stek¹ įtraukiame tik .

Parametro t reikšmė turi būti perskaičiuojama. Kadangi tarp vienetukų gali būti tik , tai . Be to, jei šiuo atveju t tampa lygus 0, tai .

Žemiau pateiktas derinių generavimo minimalaus pokyčio tvarka algoritmas. Šiame algoritme stekas organizuojamas masyvu , o jo viršutinis elementas yra (žr. treči¹jį Grėjaus kodų generavimo algoritm¹). Kadangi , tai ekvivalentu, kad į stek¹ įtraukiame .

const nn =

type mas = array [0..nn] of integer;

var n, i, k : integer;

g, tau : mas;

procedure der (n, k : integer);

var i, j, t : integer;

g, tau : mas;

begin

for j := 1 to k do

begin

g [j] := 1;

tau [j] := j + 1;

end

for j := k + 1 to n + 1 do

begin

g [j] := 0;

tau [j] := j + 1;

end

t := k;

tau [1] := k + 1;

i

while i <> n + 1 do

begin

writeln

for j := n downto 1 do write (g [j] : 3);

writeln

i := tau [1];

tau [1] := tau [i];

tau [i] := i + 1;

if g [i] = 1 then

begin

if t <> 0 then g[t]:=1-g[t]

else g[i-1]:=1-g[i-1];

t:=t+1;

end

else

begin

if t <> 1 then g [t – 1] := 1 – g [t – 1]

else g [i – 1] := 1 – g [i – 1];

t := t – 1;

end

g [i] :=1 – g [i];

if (t = i – 1) or (t = 0) then t := t + 1

else

begin

t := t – g [i – 1];

tau [i – 1] := tau [1];

if t = 0 then tau [1] := i – 1

else tau [1]:=t+1;

end

end

end

begin

writeln ('įveskite n');

readln (n);

writeln ('įveskite k');

readln (k);

der (n, k);

end

Atsitiktinio derinio generavimas

Aptarsime atsitiktinio poaibio, turinčio k elementų, iš aibės, turinčios n elementų , generavim¹. Aišku, kad tokio poaibio generavimo tikimybė yra .

Tam tikslui atsitiktinai parenkame vien¹ iš n elementų (pasirinkimo tikimybė ) ir po to atsitiktinai generuojame -elementį poaibį iš likusių elementų.

Tada šios procedūros eigoje k-elemenčio poaibio išsirinkimo tikimybė yra tokių tikimybių sandauga:

P (pirmasis išsirinktas elementas – vienas iš k elementų

P (antrasis išsirinktas elementas – vienas iš k – 1 likusių elementų)

_ _ __ _ _ __ _ _ __ _ _ __ _ _ __ _ _ _

P (k-asis išsirinktas elementas – paskutinysis iš likusių elementų) .

Ši sandauga bus lygi:

Aptarsime atsitiktinio derinio generavimo algoritm¹.

Algoritmo realizavimui panaudosime papildom¹ masyv¹ p, kuriame saugosime dar neišrinktų elementų numerius. Po to, kai pirmieji elementai išsirinkti, tai bus s¹rašas elementų, kurie dar neišsirinkti. Kadangi nebūtina išsaugoti elementų tvark¹, tai, išsirinkus element¹ , , įjo viet¹ įrašome neišsirinkt¹ element¹ .

Žemiau pateikiamas atsitiktinio derinio generavimo algoritmas.

begin

for j := 1 to n do p [j] := j;

R Æ

for j := 1 to k do

begin

r := rand (j, n);

R := R È

p [r] := p [j];

end

end

Kėlinių generavimo algoritmai

Kėlinių generavimo leksikografine tvarka algoritmas

Aptarsime kėlinių iš n elementų generavimo leksikografine tvarka uždavinį. Sprźsdami šį uždavinį, laikysime aukščiau pateiktos (žr. 3.4 paragrafo pradži¹) kombinatorinų objektų generavimo algoritmo struktūros. Norėdami išsiaiškinti šio algoritmo pagrindinius momentus, panagrinėkime pavyzdį, kai .

Pradinio kodo generavimas. Kėlinį talpinsime masyve , kurio elementai ir nusako kėlinį. Aišku, kad pradinis kėlinys yra . Pavyzdžiu, jei , tai .

Paties mažiausio, leksikografiškai didesnio kėlinio nei nagrinėjamas, apskaičiavimas. Tarkime, – nagrinėjamas kėlinys. Pavyzdžiui, . Jei į kėlinį žiūrėsime kaip į skaičių, tai reikia rasti patį mažiausi¹ skaičių, didesnį nei nagrinėjamas. Tam tikslui reikia:

rasti pirm¹ iš dešinės por¹ toki¹, kad ,

rasti , t.y tarp elementų rasti patį mažiausi¹ element¹, didesnį už ,

elementus ir sukeisti vietomis,

elementus (“uodeg¹”) surašyti atvirkščia tvarka (“apversti”).

Pavyzdžiui, pirmoji iš dešinės pora, tenkinanti 1) punkto reikalavim¹, yra , o elementas . Tada, sukeitź 4 su 5, gausime . “Apvertź uodeg¹”, gausime patį mažiausi¹ leksikografiškai didesnį kėlinį nei duotas: .

Generavimo pabaigos s¹lyga. Aišku, kad pats didžiausias kėlinys yra (masyvo elementas yra pagalbinis, ir jo reikšmė lygi nuliui). Tada pirma iš dešinės pora , tenkinanti s¹lyg¹ yra . Kitaip tariant, jei , tai generavimo pabaiga.

Vadinasi, kėlinių generavimo leksikografine tvarka algoritmas gali būti užrašytas taip.

begin

fo i:= 0 to n do p [i] :=i;

t := true;

while t do

begin

spausdinti

i := n – 1;

while p [i] > p [i+ 1] do i := i – 1;

if i = 0 then t := false

else

begin

j := n;

while p [j] < p [i] do j := j – 1;

pp := p [i]; p [i] := p [j]; p [j] := pp;

k := i + 1; l := n;

while k < l do

begin

pp := p [k]; p [k] := p [l]; p [l] := pp;

k := k + 1; l := l – 1;

end

end

end

end

Kėlinių generavimas antileksikografine tvarka

Be kėlinių generavimo leksikografine tvarka naudojamas ir kėlinių generavimo antileksikografine tvarka metodas.

Apibrėžimas. Vektorius yra antileksikografiškai mažesnis už vektorių (žymime ), jei egzistuoja toks , kad , o , . Pastebėsime, jei vietoje skaičių paimtume raides , išdėstytas natūralia, pavyzdžiui, abėcėlės tvarka: , tai leksikografinė tvarka apibrėš n ilgio žodžių išsidėstym¹ žodyne įprasta tvarka. Tuo tarpu antileksikografinė tvarka apibrėžia žodžių tvark¹, kai tiek pozicijų eiliškumas sekoje, tie ir aibės elementų išsidėstymas žodyje yra atvirkščias.

Pavyzdžiui, užrašykime aibės kėlinius leksikografine ir antileksikografine tvarka.

Leksikografine tvarka:

1, 3, 2; 2, 1, 3; 2, 3, 1; 3, 1, 2; 3, 2, 1.

Antileksikografine tvarka:

2, 1, 3; 1, 3, 2; 3, 1, 2; 2, 3, 1; 3, 2, 1.

Iš leksikografinės tvarkos kėlinio 1, 3, 2 gausime antileksikografinės tvarkos kėlinį, jei 1-t¹ keisime 3-tu, 3-t¹ keisime 1-tu (imame aibės X elementus atvirkščia tvarka) ir kėlinio pozicijas surašome atvirkščia tvarka. Gausime 3, 1, 2, o po to 2, 1, 3.

Kėlinių generavimas antileksikografine didėjimo tvarka yra labai panašus į kėlinių generavimo leksikografine didėjimo tvarka algoritm¹. Kėlinių generavimui įveskime masyv¹ , kurio elementai apibrėžia nagrinėjam¹jį kėlinį.

Pradinio kėlinio generavimas. for i := 1 to n + 1 do p [i] := i;

Paties mažiausio antileksikografiškai didesnio kėlinio apskaičiavimas. Tam tikslui reikia:

rasti pirm¹ iš kairės por¹ , toki¹, kad

rasti , t.y tarp elementų rasti patį didžiausi¹ element¹, mažesnį nei ,

elementus ir sukeisti vietomis,

elementus surašyti atvirkščia tvarka.

Generavimo pabaigos s¹lyga. Paskutinysis antileksikografinės tvarkos kėlinys yra , o , t.y. masyvo elementai yra . Aišku, kad šiuo atveju pirmoji iš dešinės pora , tenkinanti 1)-ojo punkto reikalavim¹: , yra . Vadinasi, jei , tai generavimo pabaigos s¹lyga.

Pateiksime kėlinių generavimo antileksikografine tvarka algoritm¹.

begin

fo i:= 0 to n + 1 do p [i] :=i;

t := true;

while t do

begin

spausdinti

i

while p [i-1] > p [i] do i := i + 1;

if i = n + 1 then t := false

else

begin

j

while p [j] > p [i] do j := j + 1;

pp := p [i]; p [i] := p [j]; p [j] := pp;

k := 1; l := i - 1;

while k < l do

begin

pp := p [k]; p [k] := p [l]; p [l] := pp;

k := k + 1; l := l – 1;

end

end

end

end

Kai , tai pateiktas algoritmas apskaičiuos kėlinius:

Kėlinių generavimas minimalaus pokyčio tvarka

Panagrinėkime kėlinių generavimo minimalaus pokyčio tvarka metod¹ ir algoritm¹. Kėlinių minimalaus pokyčio tvarka – tai tokia kėlinių generavimo seka, kai bet kokie du gretimi kėliniai skiriasi tik dviejų elementų padėtimi. Pavyzdžiui, kai , gautume sek¹: 1, 2, 3; 1, 3, 2; 3, 1, 2; 3, 2, 1; 2, 3, 1; 2, 1, 3.

Aptarsime kėlinių generavimo tokia tvarka metod¹.

Kai , tai egzistuoja vienintelis kėlinys: 1. Tarkime, kad turime kėlinius, tenkinančius minimalaus pokyčio tvark¹. Tada kėlinį generuosime taip.

Sunumeruokime visus kėlinius numeriais nuo 1 iki . Tada, jei kėlinio iš elemento numeris yra nelyginis skaičius, tai prie šio kėlinio prirašykime element¹ n iš dešinės ir nuosekliai atlikime visus galimus to elemento postūmius į kairź. Jei kėlinio iš elemento numeris yra lyginis, tai prie jo prirašykime element¹ n iš kairės ir nuosekliai atlikime visus galimus to elemento postūmius į dešinź.

Atlikź šiuos veiksmus, gausime kėlinių minimalaus pokyčio sek¹ (žr. 3.4.2 pav.).

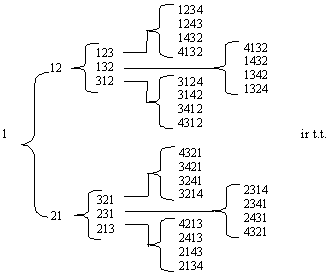
3.4.2 pav. Kėlinų generavimas minimalaus pokyčio tvarka

Aptartas kėlinių minimalaus pokyčio sekos generavimo metodas neatitinka aukščiau pateiktos kombinatorinių objektų generavimo algoritmo schemos: skaičiavimo eigoje reikia saugoti visus kėlinius. Literatūroje [RND80] pateikta šio metodo realizacija, atitinkanti kombinatorinių objektų generavimo algoritmo scem¹.

Aptarkime ši¹ realizacij¹.

Įveskime tris masyvus: , ir .

Masyvo p elementai apibrėš nagrinėjam¹ kėlinį. Elementai p₀ ir p_n+1 yra pagalbiniai elementai.

Masyvo a elementai nusako atvirkštinį kėlinį: a_k nurodo viet¹ (adres¹), kurioje masyve p yra elementas k. Kitaip tariant, . Masyvo d elementai apibrėžiami taip:

Kėlinyje elementas i “stumiamas” iki jis pasiekia element¹, didesnį už jį patį. Tada yra keičiama šio elemento judėjimo kryptis ir bandoma “stumti” (jei galima) element¹ i – 1. Kadangi turime masyv¹ a, tai šis elementas lengvai randamas masyve p.

Tam, kad nutrauktume elemento n judėjim¹, į masyv¹ p įvesti du papildomi elementai ir , kurių reikšmės yra lygios .

Elemento reikšmė yra lygi 0, nes p elemento, lygaus vienetui, judinti nereikia. Tai sekos generavimo pabaigos s¹lyga.

Kėlinių generavimo minimalaus pokyčio tvarka algoritmas

begin

for i := 1 to n do begin

p [i] := i;

a [i] := i;

d [i] := –1;

end

d [1] := 0; p [0] := n + 1; p [n + 1] := n + 1; t := true;

while t do

begin

Spausdinti ();

m := n;

while p [a [m] + d [m]] > m do begin

d [m] := – d [m];

m := m – 1;

end

if m = 1 then t := false

else

begin

pp := p [a [m]];

p [a [m]] := p [a [m] + d [m]];

p [a [m] + d [m]] : =pp;

pp := a [m]; k := p [a [m]];

a [m] := a [k];

a [k] : =pp;

end

end

end

Kai , pateiktas algoritmas apskaičiuoja:

Atsitiktinio kėlinio generavimas

Tarkime, kad – bet koks kėlinys. Perskaičiuokime šį kėlinį pagal algoritm¹:

begin

for i := n downto 2 do

sukeisti p [i] su p [rand (1, i)],

čia rand k, l tolygiai pasiskirsčiusių atsitiktinių skaičių iš atkarpos k, l generavimo procedūra

end

Taip gautas kėlinys p su tikimybe gali sutapti su bet kuriuo kėliniu iš visų kėlinių aibės.

Tam, kad įrodytume, jog visi kėliniai vienodai galimi, pasinaudokime matematinės indukcijos metodu.

Kai – akivaizdu.

Tarkime, kad algoritmas generuoja atsitiktinį kėlinį, kai elementų skaičius yra . Tegu yra bet kuris aibės kėlinys. Tada tikimybė, kad yra:

Aibės išskaidymas

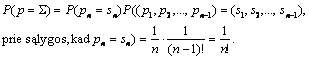
n-elementės aibės X išskaidymas į k poaibių (blokų) – tai aibės X poaibių šeima , kurios elementai tenkina reikalavimus:

Poaibius vadinsime blokais.

Aibės X visų galimų išskaidymų į k blokus aibź žymėsime , o aibės X visų galimų išskaidymų aibź žymėsime . Aišku, kad

Su aibės X išskaidymu į blokus yra susijź Stirlingo ir Belo skaičiai.

Antrosios rūšies Stirlingo skaičius – tai skirtingų n-elementės aibės išskaidymo į k blokus skaičius, t.y.

čia .

Pavyzdžiui, , kadangi yra 7 skirtingi 4-ių elementų aibės išskaidymo į du blokus būdai:

Akivaizdu, kad , kai . Be to, , kadangi tuščia blokų aibė sutinkamai su apibrėžimu yra tuščiosios aibės išskaidymas.

Su antrosios rūšies Stirlingo skaičiais, kaip ir su binominiais koeficientais, yra susijź daug tapatybių.

Pirmiausia įrodysime tapatybź, primenanči¹ derinių sudėties savybź, kuri yra susijusi su Paskalio trikampiu:

a)    , ,

b)   , ,  (3.4.2)

c)    , .

Formulių ir teisingumas akivaizdus. 3.4.1 a) formulės teisingum¹ įrodysime taip. Visus n-elementės aibės išskaidymus į k blokų suskirstykime į dvi klases. Pirmajai klasei priskirkime visus išskaidymus, kuriuse yra vienelementinis blokas , o antrajai klasei priskirkime visus išskaidymus, kai elementas n yra didesnio bloko (mažiausiai dviejų elementų aibės) elementas.

Aišku, kad pirmosios klasės galia yra , t.y. tokia, kokia yra aibės išskaidymo į blokus galia.

Antrosios klasės galia yra , kadangi prie kiekvieno išskaidymo į k blokus k skirtingais būdais galima prijungti element¹ n: elementas n paeiliui jungiamas prie kiekvieno bloko.

(1.3.4) formulė įgalina lengvai apskaičiuoti . Žemiau pateikta reikšmių lentelė, primenanti Paskalio trikampį.

Ši¹ lentelź galima traktuoti kaip “Stirlingo trikampį”. i-osios eilutės elementas yra lygus -osios eilutės elemento iš kairės ir -osios eilutės elemento iš viršaus, padauginto iš k, sumai.

6 lentelė. Antrosios rūšies Stirlingo skaičiai

Antrosios rūšies Stirlingo skaičiai yra susijź su n- osios eilės polinomo , užrašyto bazėje , užrašymu bazėje , čia

Teorema [Lip88]. Kiekvienam

Pavyzdžiui, .

Iš tikro,

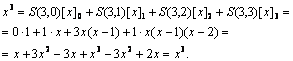
Pirmosios rūšies Stirlingo skaičiai. Šie skaičiai žymimi ir jie yra koeficientai prie x laipsnių daugianaryje , t.y.

Kitaip tariant, skaičiai vaidina atvirkšči¹ vaidmenį atžvilgiu , t.y. leidžia polinom¹, užrašyt¹ bazėje pervesti į polinomo užraš¹ bazėje .

Nesunku parodyti (palyginant koeficientus prie laipsnių lygybėje ), kad tenkina s¹ryšius:

, ,

, ,  (3.4.3)

, .

Žemiau pateikta pirmosios rūšies Stirlingo skaičių lentelė.

7 lentelė. Pirmosios rūšies Stirlingo skaičiai

Belo skaičius B_n. Belo skaičius – tai visų galimų n-elementės aibės X išskaidymo į blokus skaičius:

, čia .

Kitaip tariant,

Įrodysime Belo skaičius siejantį rekurentinį s¹ryšį:

, .  (3.4.4)

Aibės visų galimų išskaidymų aibź galima išskaidyti į klases, priklausomai nuo bloko B, turinčio savyje element¹ , arba, kas ekvivalentu, priklausomai nuo aibės . Kiekvienai aibei 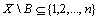egzistuoja tiksliai aibės X išskaidymų, turinčių savyje blok¹ B. Grupuodami klases priklausomai nuo aibės galios, gauname (3.4.3) formulź.

Žemiau pateikta Belo skaičių lentelė.

8 lentelė. Belo skaičiai

Aibės išskaidymo generavimo algoritmas

Aptarsime n-elementės aibės visų galimų išskaidymų generavimo algoritm¹. Šio algoritmo idėj¹ lengviausia paaiškinti suformulavus j¹ rekurentinėje formoje.

Aišku, kad kiekvienas aibės išskaidymas p vienareikšmiškai nusako aibės išskaidym¹ p_n , gaut¹ iš išskaidymo p, kai iš jo atitinkamo bloko pašalinamas elementas n (ir pašalinamas tuščiasis blokas, jei elementas n sudarė vienelementį blok¹).

Ir atvirkščiai, jei turime aibės išskaidym¹ , tai lengva rasti visus aibės išskaidymus p, kad , t.y.

(3.4.5)

Ši savybė įgalina sudaryti paprast¹ rekurentinį metod¹, generuojantį visus galimus aibės išskaidymus: jei mes žinome aibės visų galimų išskaidymų s¹raš¹ L_n-1, tai visų galimų aibės išskaidymų s¹rašas L_n gaunamas pakeičiant kiekvien¹ s¹rašo L_n-1 išskaidym¹ s (3.4.5) seka. Be to, nesunku pastebėti, jei kas antram s¹rašo s¹rašo L_n-1 išskaidymui s invertuosime (rašysime atvirkščia tvarka) (3.4.5) sek¹, tai s¹rašo L_n gretimi išskaidymai mažai skirsis vienas nuo kito. Tiksliau kalbant, kiekvienas gretimas s¹rašo L_n išskaidymas bus gautas iš prieš jį esančio išskaidymo pašalinant kažkokį element¹ iš kažkurio bloko ir patalpinant šį element¹ į kit¹ blok¹, arba sukuriant iš jo vienelementinį blok¹. Pavyzdžiui, jei , tai gausime tokius s¹rašus:

Toliau aptarsime nerekurentinź šio metodo realizacij¹.

Aibės išskaidymo blokus surašysime jų mažiausio elemento didėjimo tvarka. Bloko mažiausi¹ element¹ mes vadinsime bloko numeriu. Reikia pažymėti, kad gretimų blokų numeriai bendru atveju nėra iš eilės ein¹ natūralieji skaičiai.

Šiame algoritme naudosime kintamuosius ir , , atitinkamai reiškiančius prieš ir po bloko, kurio numeris i, stovinčių blokų numerius. Jei blokas, kurio numeris i, yra paskutinysis išskaidymo blokas, tai .

Naudosime kintam¹jį , . Jei , tai reiškia, kad i-tasis aibės elementas priklauso blokui, kurio numeris k.

Elemento judėjimo kryptį nusakys kintamasis , . Jei , tai elementas i “juda” pirmyn.

Žemiau pateiktas algoritmas generuoja visus galimus aibės išskaidymo būdus, kai duotas aibės elementų skaičius n. Algoritmo rezultatas: visų galimų aibės išskaidymų seka, kurioje kiekvienas išskaidymas gaunamas iš prieš tai buvusio, perkeliant vienintelį element¹ į kit¹ blok¹.

begin

for i := 1 to n do

begin

blok [i] := 1; pirmyn [i] := true;

end

sek

Atspausdinti išskaidym¹

elementai, masyve blok pažymėti tuo pačiu numeriu k,

priklauso k-ajam blokui.

j := n;

while j > 1 do

begin

k := blok [j];

if pirmyn [j] then

begin

if sek [k] := 0 then

begin

sek [k] := j; prec [j] := k; sek [j] := 0;

end

if sek [k] > j

begin

prec [j] := k;

sek [j] := sek [k];

prec [sek [j]] := j; sek [k] := j;

end

blok [j] := sek [k]

end

else

begin

blok [j] := prec [k];

if k = j then

if sek [k] = 0 then sek [prec [k]] := 0;

else

begin

sek [prec [k]] := sek [k];

prec [sek [k]] := prec [k];

end

end

Atspausdinti išskaidym¹.

j := n;

while ((j > 1) and ((pirmyn [j]) and (blok [j] = j))

or ((not pirmyn [j]) and (blok [j] := 1))) do

begin

pirmyn [j] := not pirmyn [j];

j := j – 1;

end

end

end

Pateiktas algoritmas pradžioje generuoja išskaidym¹ , t.y. pirm¹jį aibės išskaidym¹ s¹raše L_n, kuris gaunamas aukščiau aprašytu rekurentiniu metodu.

Pagrindinio ciklo “while j > 1 do” paskirtis yra “aktyvaus” elemento j radimas ir jo perkėlimas į kaimyninį blok¹, t.y. į blok¹ iš dešinės, jei pirmyn [j] turi reikšmź true (šiuo atveju gali būti sukuriamas blokas ), ir į blok¹ iš kairės, jei pirmyn [j] = false.

Iš aukščiau pateikto rekurentinio metodo išplaukia, kad elementas j gali būti “judinamas”, kai visi didesni už jį elementai pasiekia savo ribinź kairi¹j¹ arba dešini¹j¹ padėtį. Kitaip tariant, “aktyvusis elementas” j* yra toks elementas, kai visi didesni už jį elementai j (j > j*) tenkina vien¹ iš dviejų s¹lygų:

a)      pirmyn [j] and (blok [j] = j), t.y. elementas juda pirmyn (į dešinź) ir pasiekia savo dešini¹j¹ ribinź padėtį (aišku, kad j negali būti elementu bloko, kurio mažiausias elementas yra didesnis už j);

b)      not pirmyn [j] and (blok [j] = 1), t.y. elementas juda atgal (į kairź) ir pasiekia savo kairi¹j¹ ribinź padėtį.

Aišku, kad, jei elementas j tenkina vien¹ iš minėtų s¹lygų, tai keičiama jo judėjimo kryptis.

Paanalizuokime “aktyvaus” elemento perkėlimo į kit¹ blok¹ proces¹.

Pirmiausia randamas numeris bloko, kuriame yra aktyvusis elementas. Tarkime, kad tokio bloko numeris yra k.

Jei “aktyvusis” elementas “juda” į dešinź, tai pakanka perkelti jį į blok¹, kurio numeris yra , jei ir .

Jei arba , tai pirmiausia reikia modifikuoti reikšmź.

Tarkime, sek [k]  . Vadinasi, “aktyviojo” elemento blokas yra paskutinysis išskaidymo blokas. Šiuo atveju bus sudaromas naujas blokas . Tam tikslui pakanka priimti: ir atitinkamai pakeisti ir reikšmes (žr. algoritmo tekst¹).

Tarkime, sek [k] > j. Tai reiškia, kad visi blokai, esantys dešiniau bloko k, sudaryti iš elementų, didesnių nei j (visi tie elementai užima ribinź dešinź padėtį). Vadinasi, (žr. rekurentinį metod¹), šiuo atveju reikia sukurti vienelementį blok¹ . Tai ir įvykdoma (žr. algoritmo tekst¹).

Situacijoje, kai “aktyvusis” elementas juda atgal (į kairź), pakanka patalpinti šį element¹ į prieš blok¹ k stovintį blok¹ ir atlikti atitinkamus masyvų sek ir prec elementų pakeitimus.

Žemiau surašyti visi galimi aibės išskaidymo būdai, apskaičiuoti pagal aukščiau pateikt¹ algoritm¹.

Aišku, kad išskaidymų skaičius yra

Sveikųjų skaičių kompozicija ir išskaidymas

Nagrinėsime natūraliojo skaičiaus n išskaidym¹ į neneigiamų sveikųjų skaičių sek¹, kad .

Jei skaičių tvarka sekoje yra svarbi, tai toks skaičiaus n išskaidymas vadinamas kompozicija. Šiuo atveju paprastai įvedamas apribojimas: , .

Jei skaičių tvarka nesvarbi ir , tai yra multiaibė (aibė su pasikartojančiais elementais) ir vadinama skaičiaus n išskaidymu.

Pavyzdžiui, jei , tai (3), (1, 2), (2, 1), (1, 1, 1) yra skaičiaus 3 kompozicija, o (3), (1, 2), (1, 1, 1) – išskaidymas.

Kompozicija

Nagrinėjant kompozicij¹, į skaičių n patogu žiūrėti kaip į atkarp¹, sudaryt¹ iš vienetinio ilgio atkarpėlių, ir atkarpėlių susijungimo vietos pažymėtos taškais.

Pavyzdžiui, kai , turėsime (žr. 3.4.2 pav.).

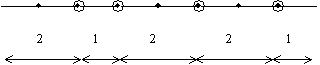
3.4.2 pav. Grafinis kompozicijos (2, 1, 2, 2, 1) vaizdavimas

Tada kompozicijos elementai yra atstumas tarp gretimų pažymėtų taškų. 3.4.2 pav. pavaizduota skaičiaus kompozicija (2, 1, 2, 2, 1). Aišku, kad kiekvien¹ kompozicij¹ galima vaizduoti dvejetainiu skaičiumi, turinčiu skiltį: vienetinė skiltis rodo pažymėt¹ tašk¹. Pavyzdžiui, kompozicijos (2, 1, 2, 2, 1) kodas yra .

n skaičiaus kompozicija, susidedanti iš k dalių, atitinka -skiltį dvejetainį skaičių, turintį vienetuk¹, ir todėl egzistuoja tokių kompozicijų.

Išskaidymas

Išskaidymas skiriasi nuo kompozicijos tuo, kad komponentų tvarka nesvarbi. Pavyzdžiui, išskaidymo atveju nedarome skirtumo tarp tokių skaičiaus 4 išskaidymų: , , . Nagrinėjant skaičiaus n išskaidym¹, patogu komponentes išdėstyti didėjimo tvarka, t.y. .

Skaičiaus n išskaidym¹ į l komponentes patogu generuoti leksikografine tvarka, pradedant išskaidymu , , ir tźsiant proces¹ tokiu būdu: norėdami gauti leksikografiškai didesnį išskaidym¹ nei nagrinėjamas, nagrinėjame elementus iš dešinės į kairź iki rasime pirm¹jį element¹ , tenkinantį s¹lyg¹ ; po to keičiame visiems , ir elementui p_l suteikiame reikšmź .

Pavyzdžiui, jei , ir nagrinėjame išskaidym¹ , tai gausime, kad pirmasis iš dešinės vienetukas tenkina s¹lyg¹ . Todėl kitas išskaidymas bus .

Jei nei vienas išskaidymo elementas netenkina s¹lygos , tai generavimo procedūra baigiama.

Žemiau pateikiamas aptarto metodo algoritmas.

Skaičiaus n išskaidymų generavimo leksikografine tvarka algoritmas

begin

l

p [1] := n;

p

while l £ n do

begin

spausdinti

i := l – 1;

while p [l] – p [i] < 2 do i := i – 1;

if i ¹ 0 then for j := i to l – 1 do p [j] := p [i] + 1

else

begin

for j := 1 to l do p [j] := 1;

l := l + 1:

end

end

end

Skaičiaus n išskaidymo algoritm¹ galima iš esmės pagerinti. Skaičiaus n išskaidym¹ galima užrašyti taip:

čia rodo, kad komponentė į išskaidym¹ įeina kartų, t.y.

Pasinaudojant tokiu išskaidymo užrašymu ir generuojant išskaidymus taip, kad , galima gauti efektyvesnį išskaidymų generavimo algoritm¹ nei aukščiau pateiktas.

Pavyzdžiui, kai , generuodami išskaidymus nurodyta tvarka, gausime toki¹ išskaidymų sek¹:

Žemiau pateiktame algoritme skaičiaus n išskaidym¹ pradėsime nuo išskaidymo . Norėdami gauti nagrinėjamam išskaidymui gretim¹ išskaidym¹, nagrinėsime patį dešinįjį išskaidymo element¹ .

Jei , tai galime pašalinti du elementus ir įvesti dar vien¹ element¹ (arba įvesti vien¹ element¹ , jei tokio elemento nagrinėjamu momentu nebuvo).

Jei , tai suma pakankamai didelė, kad galėtume įvesti dar vien¹ . Bet kuriuo atveju tas, kas lieka, paverčiama į atitinkam¹ vienetukų skaičių.

Skaičiaus n išskaidymų generavimo “žodyno” tvarka algoritmas

begin

l

p [–1] := 0; m [–1] := 0;

p [0] := n + 1;

m

p

m [1] := n;

while l ¹ 0 do

begin

spausdinti

sum := m [l] * p [l];

if m [l] = 1 then

begin

l := l – 1

sum := sum + m [l] * p [l];

end

if p [l – 1] = p [l] + 1 then

begin

l := l – 1;

m [l] := m [l] + 1

end

else

begin

p [l] := p [l] + 1;

m [l] := 1;

end

if sum > p [l] then

begin

p [l + 1] := 1;

m [l + 1] := sum – p [l];

l := l + 1

end

end

end

Aišku, kad pateiktas algoritmas yra tiesinis, kadangi skaičius operacijų, reikalingų pereinant nuo vieno išskaidymo prie kito, yra apribotas konstanta, nepriklausančia nei nuo n, nei nuo l.