| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Šioje paskaitoje apibrėšime matricų sandaugą, išsiaiškinsime jos savybes, išmoksime sudaryti atvirkštinę matricą ir spręsti matricų lygtis, išnagrinėsime keletą matricų taikomųjų pavyzdtių.
Tikslas
Apibrėšime iš pirmo tvilgsnio labai neįprastai atliekamą veiksmą matricų daugybą. Matysime, kad tokia matricų daugyba yra pagrįsta ir naudinga tiek teorinėms, tiek praktinėms reikmėms.
Matricų sandauga. Matricos A, kurios matmenys yra m n, ir matricos B, kurios matmenys yra n k, sandauga AB yra m k matmenų matrica C, kurios bet kuris elementas cij gaunamas sudėjus matricos A elementų iš i-osios eilutės ir atitinkamų matricos B elementų iš j-ojo stulpelio sandaugas.
Pavyzdtiui, norint apskaičiuoti sandaugos C = AB elementą c12, reikia sudėti matricos A pirmosios eilutės elementų ir atitinkamų matricos B antrojo stulpelio elementų sandaugas.
PAVYZDYS. Sudauginsime šias dvi matricas:
A = ![]() ir B =
ir B = 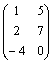 .
.
Matricos A matmenys yra 2 3, o matricos B 3 2, tai yra, matricos A stulpelių skaičius lygus matricos B eilučių skaičiui, todėl jas sudauginti galima (dar kartą atkreipkite dėmesį, kas kalbama apibrėtime apie matricų matmenis). Iš apibrėtimo dar galima nustatyti, kokiu matmenų bus sandauga C: jos eilučių skaičius lygus matricos A eilučių skaičiui, o stulpelių skaičius matricos B stulpelių skaičiui. Taigi matrica C yra 2 2 matmenų.
Dabar apskaičiuosime matricos C elementus:
c11 = 2·1 + (1)·2 + 3·(4) = 12, c12 = 2·5 + (1)·7 + 3·0 = 3,
c21 = 4·1 + 6·2 + (2)·(4) = 24, c22 = 4·5 + 6·7 + (2)·0 = 32.
Taigi
C = AB = ![]()
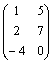 =
=
=
=![]() . ☺
. ☺
Iš apibrėtimo matyti, kad ne visada galima apskaičiuoti matricų
A ir B sandaugą BA, net jei sandaugą AB apskaičiuoti galima. Kodėl?
PAVYZDYS. Dviejų kvadratinių matricų galima apskaičiuoti abi sandaugas AB ir BA. Apskaičiuokime jas:
AB = ![]() ,
,
BA = ![]() . ☺
. ☺
Matyti, kad AB BA. Taigi matricų sandauga apskritai netenkina perstatomojo dėsnio.
Kaip galima būtų rasti tokią matricų porą,
kuri tenkina perstatomąjį dėsnį? Raskite ją.
Nesunku įrodyti, kad matricų sandauga tenkina šiuos dėsnius:
1. (AB)C = A(BC) Jungiamasis dėsnis
2. A(B + C) = AB + AC Kairysis skirstomasis dėsnis
3. (B + C)A = BA + BC Dešinysis skirstomasis dėsnis
4. k(AB) = (kA)B = A(kB), čia k yra skaičius
pavyzdyje matėme, kad matricų sandauga netenkina perstatomojo dėsnio, AB BA bendruoju atveju. Yra ir dar vienas dalykas, kuris skiria matricų sandaugą nuo skaičių sandaugos: dviejų nenulinių matricų sandauga kartais būna nulinė matrica, t.y. matrica, kurios visi elementai yra nuliai.
PAVYZDYS.Apskaičiuokime tokią sandaugą:
AB = ![]() .
.
Taigi gali atsitikti, kad AB = 0 net jei ir A 0, ir B ☺
Raskite dar tokių nenulinių matricų, kurių sandauga būtų nulinė matrica.
Įrodykite, kad bet kurios matricos A ir nulinės matricos
sandauga yra nulinė matrica: A0 = 0.
Jei yra nulinė, tai gal yra ir vienetinė matrica E: tai matrica, kurią
sudauginus su bet kokia matrica A, gaunama ta pati matrica A, AE = A?
PAVYZDYS Atsargų vertė. Baldų fabrikas turi 3 parduotuves, kurių sandėliuose saugo 5 tipų prekes. Atsargų kiekis šiuose sandėliuose surašytas matricoje P, o didmeninės ir matmeninės vieneto kainos (D ir M, tūkstančiais litų) matricoje K:
P =  K =
K = 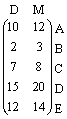
Kokia yra didmeninė ir matmeninė prekių, saugomų 1, 2 ir 3 sandėlyje, kaina (atskirai)?
P·K =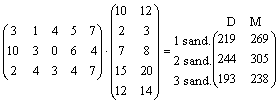 ☺
☺
PAVYZDYS. Apskaičiuosime kvadratinės matricos A ir matricos stulpelio X sandaugą:
AX =  ·
·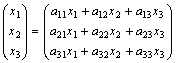
Kas yra gautosios sandaugos elementai? ☺
PAVYZDYS. Rinkos dalies prognozė (Markovo[1] grandinės). Mieste yra 100 000 potencialių pirkėjų. Per vieną konkretų mėnesį 40 000 iš jų gali pirkti Maksimoje, po 30 000 parduotuvėje Iki, ir Eko. Tą faktą, kad pirkėjas perka kurioje nors parduotuvėje, vadinsime būsena ir sunumeruosime jas: 1, 2 ir 3. Šių būsenų tikimybės yra
![]()
Jas surašykime į vienos eilutės matricą tokios matricos vadinamos vektoriais: (0,4; 0,3; 0,3). Jį vadinsime būsenų tikimybių vektoriumi ir tymėsime p(1), čia 1 reiškia pirmą tyrimo mėnesį:
p 0,3 0,3).
Beje, šios tikimybės turi ir kitą lengvai pamatomą prasmę: tai yra parduotuvės rinkos dalis pirmą tyrimo mėnesį. Iš istorinių duomenų ir sociologinių tyrimų paprastai galime sutinoti ir tikimybes, vadinamas tingsnio tikimybėmis:
Pij tikimybė pereiti iš būsenos i į būseną j (tiksliau kalbant, tai yra sąlyginė būsenos j tikimybė, jei iki šiol buvo būsena i).
Mūsų atveju jų yra devynios; surašykime jas į vieną matricą, vadinamą tingsnio matrica:
P =  .
.
Pavyzdtiui, jos elementas P23 = 0,2 reiškia trečiosios būsenos (pirkėjas eina į Eko) tikimybę, jei prieš tai buvo 2 būsena (pirkėjas pirko Iki). Atkreipkite dėmesį, kad vienos eilutės tikimybių suma lygi vienetui: būsenos yra nesuderinami įvykiai ir be šių trijų daugiau būsenų nėra.
Remiantis pilnosios tikimybės formule, pagal būsenų tikimybių vektorių ir tingsnio matricą galima prognozuoti busimas rinkas: sandauga p(1)P yra antrojo, būsimojo mėnesio būsenų tikimybių vektorius:
p p(1)P = (0,4 0,3 0,3)  =
(0,41 0,31 0,28).
=
(0,41 0,31 0,28).
Matyti, kad Maksimos ir Iki rinkos dalis padidės, o Eko sumatės. Apskaičiuokite ir trečio mėnesio būsenų tikimybių vektorių. Kaip manote, kokia yra rinka, jei galioja lygybė p(n+1) = p(n)? ☺
Pratimai
1. Kurias iš šių sandaugų galima apskaičiuoti: AB, BA, AC, CA, BC, CB? Apskaičiuokite tas, kurias galima.
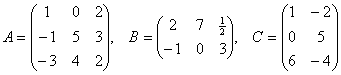
2. Pagal 4 pavyzdtio duomenis apskaičiuokite sandaugas (1 1 1)P ir (1 1 1)PK. Kokią ekonominę prasmę turi šios sandaugos?.
Realiųjų skaičių aibėje yra skaičius, vadinamas vienetu, su tokia savybe: 1·a = a·1 = a. Matricų aibėje tokios matricos apskritai nėra, tačiau kvadratinių matricų aibėje yra. Kvadratinių n-osios eilės matricų aibėje vienetinė yra matrica, tymima raide E, turinti savybę
AE = EA = A.
Nesunku būtų įrodyti (tr. 2 pratimą), kad vienetinė matrica yra taip pat kvadratinė n-osios eilės matrica, pagrindinėje jos įstritainėje yra vienetai, o visi kiti elementai nuliai. Taigi antrosios eilės matricų vienetinė yra
E = ![]() ,
,
o trečiosios eilės
E = 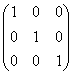 .
.
Pratimai
Apskaičiuokite sandaugas AE ir EA,
jei A = 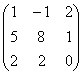 .
.
Įrodykite, kad antrosios eilės vienetinės matricos įstritainės elementai yra vienetai, o kiti elementai nuliai.
Nurodymas. Sudarykite vienetinę matricą E su netinomais elementais:
E = ![]() .
.
Remdamiesi vienetinės matricos apibrėtimu, sudarykite keturių lygčių sistemą su keturiais netinomaisiais eij, ir ją išspręskite.
Bet kuris realusis skaičius a, išskyrus nulį, turi atvirkštinį,
tymimą ![]() arba a1. Ar matricų aibėje
yra tokia matrica? Jei yra, tai kurios matricos turi atvirkštinę, o kurios
ne? Kaip sudaryti atvirkštinę matricą, jei ji yra? Kiek skirtingų atvirkštinių
matricų gali turėti viena matrica? Į visus šiuos ir kitus klausimus atsakysime
šiame skirsnyje.
arba a1. Ar matricų aibėje
yra tokia matrica? Jei yra, tai kurios matricos turi atvirkštinę, o kurios
ne? Kaip sudaryti atvirkštinę matricą, jei ji yra? Kiek skirtingų atvirkštinių
matricų gali turėti viena matrica? Į visus šiuos ir kitus klausimus atsakysime
šiame skirsnyje.
Apibrėtimas. Kvadratinės matricos A atvirkštine vadinama matrica A1 su tokia savybe:
AA1 = A1A = E.
PAVYZDYS. Remdamiesi šiuo atvirkštinės matricos apibrėtimu,
įrodysime, kad matrica A = ![]() turi atvirkštinę A1 =
turi atvirkštinę A1 = ![]() .
.
AA1 = ![]()
Jums paliksime apskaičiuoti antrąją sandaugą:
A1A = ☺
Taigi iš šio pavyzdtio matyti, kad kai kurios matricos atvirkštinę turi.
Paaiškinsime, kaip sudaroma kvadratinės matricos atvirkštinė matrica A1 ir įrodysime, kad tokia matrica iš tikrųjų yra atvirkštinė ir vienintelė. Kad būtų paprasčiau, sudarysime trečiosios eilės matricos atvirkštinę (aukštesnės eilės matricų atvirkštinė sudaroma labai panašiai):
A =  .
.
Apskaičiuokime šios matricos determinantą |A|, t.y. trečiosios eilės determinantą, sudarytą iš tokių pačių elementų, kaip ir matrica A:
|A| =  .
.
Sakykime, kad jis nelygus nuliui: |A| 0. Dar sudarykime ir apskaičiuokime visus matricos A adjunktus: A11, A12, A13, A21, A22, A23, A31, A32, A33. Iš jų sudarykime tokią matricą:
A* =  .
.
Atkreipkite dėmesį į adjunktų išdėstymo tvarką jų indeksus. Padaliję ją iš matricos A determinanto |A|, gausime matricos A atvirkštinę matricą:
A1 = 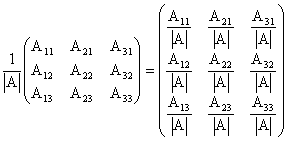
Dėl dalybos iš |A| turėjome tarti, kad matricos A determinantas yra nelygus nuliui, antraip negalėtume dalyti. Norint įrodyti, kad ši matrica iš tikro yra matricos A atvirkštinė, reikia apskaičiuoti dvi sandaugas: AA1 ir A1A; abiem atvejais turi išeiti vienetinė matrica. Tai įrodoma remiantis 8 ir 9 determinantų savybe.
Įrodymas
Taigi apskaičiuosime AA1 ir A1A:
C =  ·
· .
.
Remdamiesi
skaičiaus ir matricos daugybos savybėmis, pirmiausia sudauginsime matricas, o
tik po to gautą matricą iš skaičiaus ![]() .
Apskaičiuosime tik du būdingus sandaugos matricos C elementus: vieną iš
pagrindinės įstritainės, o kitą nesantį joje, nes kiti elementai apskaičiuojami
taip pat. Matysime, kad pirmasis yra vienetas, o kiti nuliai. Taigi
apskaičiuokime
.
Apskaičiuosime tik du būdingus sandaugos matricos C elementus: vieną iš
pagrindinės įstritainės, o kitą nesantį joje, nes kiti elementai apskaičiuojami
taip pat. Matysime, kad pirmasis yra vienetas, o kiti nuliai. Taigi
apskaičiuokime
c11 = ![]() .
.
Skliaustuose gautas reiškinys yra matricos determinanto |A| skleidinys pirmosios eilutės elementais. Apskaičiuokime ir elementą, esantį šalia įstritainės, pavyzdtiui,
c12 = ![]() .
.
Skliaustuose gautas reiškinys yra matricos determinanto |A| pirmosios eilutės elementų ir antrosios eilutės elementų adjunktų sandaugų suma; ji lygi 0 pagal 9º determinantų savybę.
Dėl tų pačių prietasčių ir visi kiti matricos C pagrindinės įstritainės elementai yra vienetai, o elementai, esantys šalia jos lygūs nuliui, todėl C = AA1 = E. Jums paliksime įrodyti, kad ir A1A = E. ☺
PAVYZDYS. Sudarysime matricos
A = 
atvirkštinę.
Apskaičiuosime matricos determinantą:
|A| = 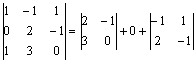 =
3 1 = 2.
=
3 1 = 2.
Apskaičiuosime adjunktus:
![]()
![]()
![]() .
.
Kadangi matricos determinantas nelygus nuliui, galime sudaryti atvirkštinę matricą:
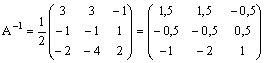 .
.
Patikrinsime:
AA1 = 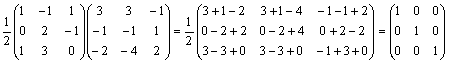 .
.
Aišku, reikia patikrinti ir sandaugą A1A; tai padaryti paliekame jums. ☺
Matricos atvirkštinė yra vienintelė. Prieštaros būdu įrodysime, kad jei matrica A turi atvirkštinę A1, tai ta atvirkštinė yra vienintelė.
Tarkime priešingai: sakykime, kad matrica A turi dvi skirtingas atvirkštines, A1 ir B. Kadangi jos yra atvirkštinės, tai abi tenkina pagrindinę atvirkštinių matricų savybę:
A1·A = E; B·A = E Þ A1·A = B·A.
Padauginkime paskutinės lygybės abi puses iš A1 iš dešinės:
(A1·A)· A1 = (B·A)·A1.
Remdamiesi skirstomuoju dėsniu, sugrupuokime taip:
A1·(A· A1) = B·(A·A1) Þ A1·E = B·E Þ A1 = B.
Tarėme, kad atvirkštinės matricos A1 ir B yra skirtingos, tačiau įrodėme, kad jos lygios. Šis prieštaravimas rodo, kad mūsų prielaida nėra teisinga. Kadangi kitų variantų nėra (dvi matricos gali būti lygios arba nelygios), tai lieka tik vienas: abi atvirkštinės yra lygios. Kadangi abi atvirkštines matricas pasirinkome laisvai, be jokių apribojimų, tai reiškia, kad skirtingų atvirkštinių nėra matricos A visos atvirkštinės yra lygios. ☺
Apskaičiuokite šių matricų atvirkštines, jei jos egzistuoja.
a) A =![]() ; b)
; b) 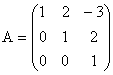 c)
c) 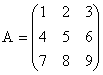 d)
d) 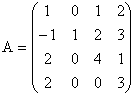 .
.
Kelias matricų lygtis jau esame išsprendę, tačiau jose tereikėjo sudėties, atimties ir daugybos iš skaičiaus veiksmų. Apibrėtę atvirkštinės matricos sąvoką, galime išspręsti ir tokias matricų lygtis, kuriose yra ir daugyba. Pavyzdtiui, prisiminę 5 pavyzdį, pamatysime, kad tiesinę 3 lygčių sistemą su 3 netinomaisiais
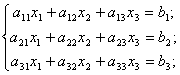
galima parašyti matricų lygtimi:
 ·
·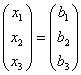 ,
,
arba dar trumpiau, AX = B. Ją galima išspręsti panašiai kaip ir skaičių algebros lygtį ax = b, tačiau reikia turėti mintyje, kad matricų algebroje nėra dalybos ją pakeičia daugyba iš atvirkštinės matricos:
|
AX = B |
Sakykime, kad matricos A atvirkštinė A1 egzistuoja (matricos A determinantas nelygus nuliui). |
|
A1AX = A1B |
Abi lygties puses padauginome iš matricos A atvirkštinės A1 iš kairės pusės (iš dešinės pusės dauginti negalima; kodėl?) |
|
EX = A1B |
A1A = E |
|
X = A1B |
EX = X. |
Taigi norint išspręsti matricų lygtį AX = B, reikia rasti matricos A atvirkštinę ir ją padauginti iš laisvųjų narių stulpelio B.
PAVYZDYS. Išspręsime lygčių sistemą
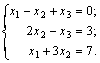
Šios sistemos matricos
A =  ,
,
atvirkštinę apskaičiavome 8 pavyzdyje:
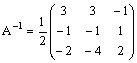
Taigi sistemos sprendinys yra
X = A1B =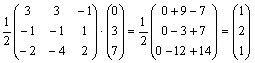 ,
,
arba x1 = 1, x2 = 2, x3 = 1. ☺
PAVYZDYS. Iš 6 pavyzdtio matyti, kad rinka bus stabili, jei galios būsenų vektorių lygybė p(n+1) = p(n) arba p(n) = p(n)P. Nustatysime, kokios turi būti būsenų tikimybės, kad rinka būtų stabili, jei tingsnio matrica yra tokia pati, kaip 6 pavyzdyje:
|
(p p p p p p ) |
Čia p p p yra būsenų tikimybės. Sudauginę būsenų vektorių su tingsnio matrica, gausime dviejų vektorių lygybę. |
|
(p p p p p p 0,1p p p 0,1p p p |
|
|
|
Pagal matricų (ir vektorių) lygybės apibrėtimą, iš dviejų vektorių lygybės gavome trijų lygčių sistemą su trim netinomaisiais. |
|
|
Šioje sistemoje viena lygtis visada yra kitų dviejų išvestinė: panariui sudėję I ir III lygtį, gautume antrąją lygtį su priešingu tenklu, todėl II lygtis yra pirmųjų dviejų išvestinė, ją atmeskime. |
|
|
Prijungėme dar vieną lygtį, kuri reiškia, kad būsenos sudaro visą įvykių grupę: kitų būsenų nėra ir būsenos yra nesuderinami įvykiai, todėl jų tikimybių suma lygi 1: |
|
|
Apskaičiavome sistemos matricos atvirkštinę |
|
|
Sudauginę su laisvųjų narių stulpeliu, gavome sprendinį stabiliąsias parduotuvių rinkos dalis. |
1. Atvirkštinės matricos metodu išspręskite šias lygčių sistemas.
a) 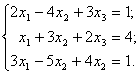 b)
b) 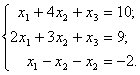 c)
c) 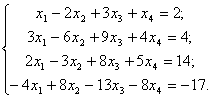
2. Pagal šias technologines matricas sudarykite ekonominės sistemos balanso modelius ir atvirkštinės matricos metodu raskite subalansuotą gamybos planą.
|
a) |
Sąnaudos |
Paklausa |
||
|
Gamyba | ||||
Atsakymas: (150, 150, 75)
|
b) |
Sąnaudos |
Paklausa |
||
|
Gamyba | ||||
Atsakymas: (100, 100, 200)
3. Apskaičiuokite stabiliąsias rinkos dalis (būsenų tikimybes) su šiomis tingsnio matricomis.
a)  b)
b)  c)
c)  d)
d) 
Kas yra nulinė matrica?
Kas yra kvadratinė matrica?
Apibrėtkite dviejų matricų sandaugą.
Kurią eilutę ir stulpelį reikia sudauginti, norint gauti sandaugos elementą, esantį pirmoje eilutėje ir trečiame stulpelyje?
Kokias matricas galima sudauginti, o kokių ne? Sugalvokite po pavyzdį.
Kokiomis savybėmis pasitymi matricų sandauga?
Ar matricų sandaugai galioja perstatomoji savybė?
Pateikite matricų pavyzdtių, kurioms galioja perstatomoji savybė.
Ar galima gauti nulinę matricą, sudėjus dvi nenulines matricas?
Kokia yra pagrindinė vienetinės matricos savybė?
Iš kokių elementų sudaryta vienetinė matrica?
Kokia yra pagrindinė atvirkštinės matricos savybė?
Kokios matricos turi, o kokios neturi atvirkštinės?
Kaip yra sudaroma atvirkštinė matrica?
Kiek matrica gali turėti skirtingų atvirkštinių?
Kaip sprendtiamos tiesinės lygčių sistemos, parašytos matricine forma?
A.Markovas (A.A.Markov, 18) rusų matematikas
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 12956
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved