| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Tegul turime ploktum¹ Π. Ploktumos ![]() bijektyvus atvaizdis f i j¹ pači¹ vadinamas
ploktumos
bijektyvus atvaizdis f i j¹ pači¹ vadinamas
ploktumos ![]() transformacija
transformacija ![]() .
Jeigu turime kokį nors ploktumos Π tak¹ M, į kurį
transformacija f atvaizduoja į tak¹
.
Jeigu turime kokį nors ploktumos Π tak¹ M, į kurį
transformacija f atvaizduoja į tak¹ ![]() :
:
![]() (
(![]() ),
tai jis vadinamas tako M vaizdu. Takas M vadinamas tako M pirmavaizdiu.
),
tai jis vadinamas tako M vaizdu. Takas M vadinamas tako M pirmavaizdiu.
Sakykime, kad turime dvi ploktumos transformacijas f ir g:
![]()
![]()
Jeigu transformacija ![]() ,
o transformacija
,
o transformacija ![]() ,
tai transformacija, kuri tak¹ M atvaizduoja į tak¹
,
tai transformacija, kuri tak¹ M atvaizduoja į tak¹ ![]() yra vadinama transformacijų f ir g kompozicija.
ymima:
yra vadinama transformacijų f ir g kompozicija.
ymima: ![]()
![]() .
.
Jei f ir g yra dvi ploktumos ![]() transformacijos, tai jų kompozicija
transformacijos, tai jų kompozicija ![]() taip pat yra bijekcija, t.y. ji yra ploktumos
taip pat yra bijekcija, t.y. ji yra ploktumos
![]() transformacija.
transformacija.
Sakykime ![]() ir
ir ![]() . Kadangi f yra bijekcija, tai į
tak¹
. Kadangi f yra bijekcija, tai į
tak¹ ![]() atvaizduoja, nes vienintelis takas M.
Vadinasi, galime apibrėti transformacij¹
atvaizduoja, nes vienintelis takas M.
Vadinasi, galime apibrėti transformacij¹ ![]() , kuri tak¹
, kuri tak¹ ![]() atvaizduoja į tak¹ M:
atvaizduoja į tak¹ M: ![]() Ji taip pat yra
bijekcija, ir vadinama transformacijos f atvirktine transformacija.
Taigi, bet kuri ploktumos transformacija turi atvirktinź transformacij¹, kuri
taip pat yra ploktumos transformacija.
Ji taip pat yra
bijekcija, ir vadinama transformacijos f atvirktine transformacija.
Taigi, bet kuri ploktumos transformacija turi atvirktinź transformacij¹, kuri
taip pat yra ploktumos transformacija.
Akivaizdu, kad transformacija ![]() ,
kuri kiekvien¹ ploktumos tak¹ M atvaizduoja į jį patį, irgi
yra ploktumos
,
kuri kiekvien¹ ploktumos tak¹ M atvaizduoja į jį patį, irgi
yra ploktumos ![]() transformacija ir vadinama tapating¹ja transformacija.
transformacija ir vadinama tapating¹ja transformacija.
Aiku, kad bet kuriai transformacijai yra
teisingos: ![]() ir
ir ![]() .
.
Bet kokių trijų
transformacijų kompozicijai yra teisingas asociatyvumo dėsnis: ![]() .
I tikrųjų:
.
I tikrųjų: ![]() ;
;
![]()
![]()
Tuomet akivaizdu, kad: ![]()
![]()
![]()
Imame: ![]()
![]()
![]()
Kadangi M yra bet koks ploktumos Π takas,
tai i čia gauname, ![]() .
I pateiktų savybių iplaukia, kad ploktumos Π visų
transformacijų aibė, kurioje yra apibrėta transformacijų
kompozicijos operacija yra grupė, transformacijų kompozicijos
atvilgiu. Tapatinga transformacija vaidina grupės vienetinio elemento
vaidmenį.
.
I pateiktų savybių iplaukia, kad ploktumos Π visų
transformacijų aibė, kurioje yra apibrėta transformacijų
kompozicijos operacija yra grupė, transformacijų kompozicijos
atvilgiu. Tapatinga transformacija vaidina grupės vienetinio elemento
vaidmenį.
Jeigu turime ploktumos figūr¹, tai figūros vaizdu, atliekant transformacij¹ f, vadiname aibź takų, kurie yra figūros Ф takų vaizdai:
![]()
Figūra Ф vadinama invariantine transformacijos f atvilgiu, jeigu ji atvaizduojama pati į save.
Tegul afininėje ploktumoje ![]() yra duotas afininis reperis
yra duotas afininis reperis ![]() .
Tuomet kiekvienas ploktumos takas A turi koordinates:
.
Tuomet kiekvienas ploktumos takas A turi koordinates: ![]() ,
,
![]() .
Jei, atlikus koki¹ tai ploktumos transformacij¹ f, takas A atvaizduojamas
į tak¹ A su koordinatėmis
.
Jei, atlikus koki¹ tai ploktumos transformacij¹ f, takas A atvaizduojamas
į tak¹ A su koordinatėmis ![]() tame pačiame reperyje, tai
tame pačiame reperyje, tai ![]() ir
ir ![]() .
.
APIBRĖIMAS. Ploktumos ![]() transformacija
transformacija ![]() yra vadinama ploktumos afinine transformacija,
jeigu kiekvieno jos tako
yra vadinama ploktumos afinine transformacija,
jeigu kiekvieno jos tako ![]() vaizdo
vaizdo ![]() koordinatės
koordinatės ![]() tiesikai isireikia per tako M koordinates
tiesikai isireikia per tako M koordinates ![]() tokiu būdu:
tokiu būdu:
![]()
![]()
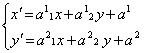 (1)
(1)
čia ![]() yra skaičiai ir determinantas
yra skaičiai ir determinantas
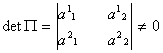
Paymėkime: 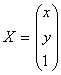 ,
, 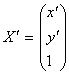 ,
tai
,
tai 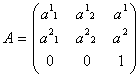 .
.
Tuomet (1) formules
galima urayti: ![]() .
Kadangi
.
Kadangi 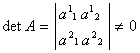 , tai matrica A yra vadinama afininės transformacijos matrica.
, tai matrica A yra vadinama afininės transformacijos matrica.
Dabar įrodysime, kad visų ploktumos ![]() afininių transformacijų aibė
yra grupė transformacijų kompozicijos atvilgiu. Sakykime, kad:
afininių transformacijų aibė
yra grupė transformacijų kompozicijos atvilgiu. Sakykime, kad:
![]()
![]()
ių afininių transformacijų
kompozicija yra taip apibrėta: ![]() .
Parodysime, kad kompozicija
.
Parodysime, kad kompozicija ![]() yra afininė transformacija. Jei
transformacijos f yra matrica
yra afininė transformacija. Jei
transformacijos f yra matrica 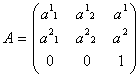 ,
o transformacijos g matrica
,
o transformacijos g matrica 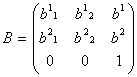 ir
ir 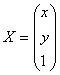
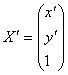
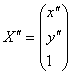 , tai transformacij¹ f matriciniu
būdu galime urayti taip:
, tai transformacij¹ f matriciniu
būdu galime urayti taip:
![]() ( 2
), o transformacija g yra:
( 2
), o transformacija g yra:
![]() ( 3
)
( 3
)
Norint urayti kompozicijos ![]() koordinatinź iraik¹, reikia matric¹ X
ireikti per matric¹ X. Įstatź į lygybź ( 3 ) matricos X iraik¹ (
2 ) gausime:
koordinatinź iraik¹, reikia matric¹ X
ireikti per matric¹ X. Įstatź į lygybź ( 3 ) matricos X iraik¹ (
2 ) gausime:
![]()
Kadangi matricų daugyba yra asociatyvi, tai: ![]() .
Paymėjź,
.
Paymėjź, ![]() ,
gausime:
,
gausime: ![]() ,
kuri, aiku, turi tokį pat pavidal¹, kaip ir matrica A. Be to, kadangi f
ir g yra afininės transformacijos, tai
,
kuri, aiku, turi tokį pat pavidal¹, kaip ir matrica A. Be to, kadangi f
ir g yra afininės transformacijos, tai ![]() ir
ir ![]() .
Tuomet, pagal matricų sandaugos determinanto formulź, gauname, kad ir
.
Tuomet, pagal matricų sandaugos determinanto formulź, gauname, kad ir ![]() ,
o tai reikia, kad transformacija
,
o tai reikia, kad transformacija ![]() yra afininė. Tokiu būdu
įrodėme, kad dviejų afininių transformacijų
kompozicija yra afininė transformacija, o jos matrica yra lygi tų
transformacijų matricų sandaugai.
yra afininė. Tokiu būdu
įrodėme, kad dviejų afininių transformacijų
kompozicija yra afininė transformacija, o jos matrica yra lygi tų
transformacijų matricų sandaugai.
Sakykime turime afininź transformacij¹
![]() . (5)
. (5)
Tuomet egzistuoja jai atvirktinė transformacija:
![]()
![]()
Įrodysime, kad ji yra afininė. Norint
rasti atvirktinės transformacijos koordinatinź iraik¹, reikia ![]() ireikti per
ireikti per ![]() .
Abi lygybės
.
Abi lygybės ![]() puses i kairės dauginame i
puses i kairės dauginame i ![]() .
Matrica
.
Matrica ![]() egzistuoja, nes
egzistuoja, nes ![]() .
Tuomet gauname:
.
Tuomet gauname: ![]() ,
t.y. turime:
,
t.y. turime: ![]() ,
kur
,
kur 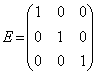 . I
. I ![]() gauname, kad:
gauname, kad: ![]() ,
ir matrica X turi tokį patį pavidal¹ kaip ir (5) iraikoje, nes
,
ir matrica X turi tokį patį pavidal¹ kaip ir (5) iraikoje, nes ![]() ir
ir ![]() .
Vadinasi transformacja f(-1) irgi yra afininė transformacija.
.
Vadinasi transformacja f(-1) irgi yra afininė transformacija.
Aiku, kad ploktumos tapatinga
transformacija ![]() irgi yra afininė transformacija, kuri¹
galime urayti taip
irgi yra afininė transformacija, kuri¹
galime urayti taip ![]() .
Jos matrica yra vienetinė matrica E, kurios determinantas nelygus nuliui.
.
Jos matrica yra vienetinė matrica E, kurios determinantas nelygus nuliui.
Taigi, tapatinga transformacija taip pat yra afininė transformacija.
Mes įrodėme, kad bet kurioms
trims ploktumos transformacijoms yra teisingas asociatyvumo dėsnis.
Aiku, kad jis teisingas ir bet kurioms trims afininėms ploktumoms. I
įrodyto seka, kad afininių transformacijų aibė yra
grupė transformacijų kompozicijos atvilgiu. Ji vadinama ploktumos
afinine grupe ir ymima ![]() .
.
Afininė transformacija f, kurios
matricos A ![]() yra vadinama tiesiogine afinine transformacija,
o kurios
yra vadinama tiesiogine afinine transformacija,
o kurios ![]() vadinama netiesiogine afinine
transformacija. Aiku, kad visų tiesioginių afininių
transformacijų aibė yra grupė, kuri¹ ymime
vadinama netiesiogine afinine
transformacija. Aiku, kad visų tiesioginių afininių
transformacijų aibė yra grupė, kuri¹ ymime ![]() .
Netiesioginių transformacijų aibė nėra grupė, nes
dviejų netiesioginių transformacijų kompozicija yra
tiesioginė transformacija.
.
Netiesioginių transformacijų aibė nėra grupė, nes
dviejų netiesioginių transformacijų kompozicija yra
tiesioginė transformacija.
Afininė transformacija f yra vadinama
ekviafinine, jeigu jos matricos A determinantas ![]() .
Ekviafininės transformacijos sudaro grupź, ymim¹
.
Ekviafininės transformacijos sudaro grupź, ymim¹ ![]() .
Transformacija f, kurios matricos
.
Transformacija f, kurios matricos ![]() ,
determinantas yra vadinamas unimoduliarine transformacija. Aiku,
kad unimoduliarinės transformacijos sudaro grupź, kuri ymima
,
determinantas yra vadinamas unimoduliarine transformacija. Aiku,
kad unimoduliarinės transformacijos sudaro grupź, kuri ymima ![]() ir vadinama ploktumos unimoduliarine grupe.
Visos afininės transformacijos, kurios tak¹ X atvaizduoja į tak¹
taip:
ir vadinama ploktumos unimoduliarine grupe.
Visos afininės transformacijos, kurios tak¹ X atvaizduoja į tak¹
taip: ![]() ,
vadinamos centro afininėmis transformacijomis.
,
vadinamos centro afininėmis transformacijomis.
Jeigu ![]() ,
,
![]() ,
tai ir
,
tai ir ![]() .
Kadangi f ir g yra centro afininės transformacijos, tai ir jų
kompozicija
.
Kadangi f ir g yra centro afininės transformacijos, tai ir jų
kompozicija ![]() centro afininė transformacija. Jeigu
centro afininė transformacija. Jeigu ![]() ,
tai ir
,
tai ir ![]() tuomet, centro afininei transformacijai
atvirktinė transformacija f(-1) irgi yra centro afininė
transformacija. Tapatinga transformacija id irgi yra centro afininė
transformacija. Taigi centro afininių transformacijų aibė yra
grupė
tuomet, centro afininei transformacijai
atvirktinė transformacija f(-1) irgi yra centro afininė
transformacija. Tapatinga transformacija id irgi yra centro afininė
transformacija. Taigi centro afininių transformacijų aibė yra
grupė ![]() ,
vadinama tako X stabilizatoriumi. Visos ivardintos transformacijų
grupės yra afininių transformacijų grupės pogrupiai.
,
vadinama tako X stabilizatoriumi. Visos ivardintos transformacijų
grupės yra afininių transformacijų grupės pogrupiai.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1141
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved