Tikimybiø teorija ir statistika

KAUNO TECHNOLOGIJOS UNIVERSITETAS

Tikimybiø teorija ir statistika

Antrasis Namø darbas

(16 variantas)

Dvimatis atsitiktinis dydis (X, Y) tolygiai pasiskirstês trikampëje srityje ABC, t.y. jo tankis

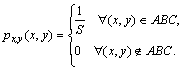
Èia S – trikampio ABC plotas. Užrašykite vienmaèius tankius p_x(x), p_y(y) ir kovariacinê matric¹. Ar dydžiai X ir Y yra priklausomi, ar koreliuoti? Apskaièiuokite D(3X – 2Y).

Pastaba. Viršûniø A(-3; 0), B( ) ir C( ) koordinatës nurodytos staèiakampëje sistemoje.

Užrašome trikampio kraštiniø lygtis:

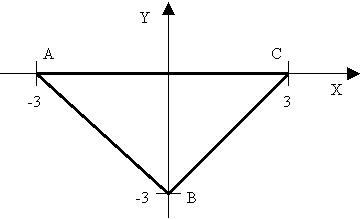
AB : y = -x-3

BC : y = x -3

AC : y = 0

Trikampio ABC plotas lygus 9, taigi, dvimaèio atsitiktinio dydžio (X, Y) tankio funkcija yra

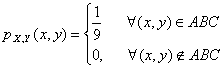
Tada vienmaèiø atsitiktiniø dydžiø X ir Y tankio funkcijos

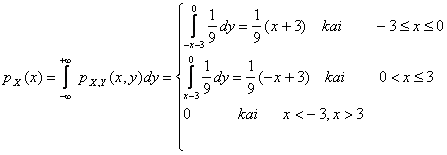
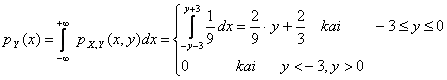
Randame viemaèiø atsitiktiniø dydžiø X ir Y vidurkius

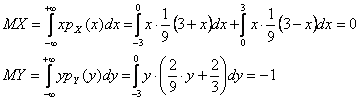
Tai pat apskaièiuojame jø dispersijas

Kovariacija yra

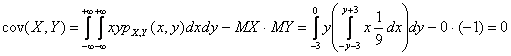
Tada kovariacinë matrica yra lygi:

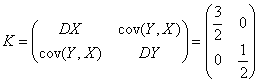
Kadangi atsitiktiniø dydžiø X ir Y kovariacija lygi 0, tai dydžiai nekoreliuoti, taèiau , t.y atsitiktiniai dydžiai yra nepriklausomi.

Apskaièiuojame dispersij¹ D(3X-2Y):

Duota seka nepriklausomø atsitiktiniø dydžiø X₁, X₂,…, X_k,… Dydis X_k su vienodomis tikimybëmis gali ágyti tik dvi reikšmes k^a arba -k^a. Ar galioja šiai sekai didžiøjø skaièiø dësnis, kai parametras a a a ? Jeigu galioja, užrašykite já. Èia a , a .

Kai k = 1,2 …

Pakankamos s¹lygos, kad galiotø didžiøjø skaièiø dësnis:

A.    

Arba

B.    

Apskaièiuojame atsitiktiniø dydžiø vidurkius ir dispersijas:

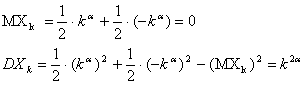
Nagrinëjame kai . Tada dispersijos lygios:

Kaip matome, kad   visiems k =1,2,…

S¹lyga (A) yra tenkinama, t.y. pagal Èebišovo teorem¹ sekai galioja didžiøjø skaièiø dësnis.

Kiekvienam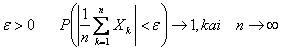

Kai , tai , t.y.:

, taigi, dispersijos DX_k neapibrëžtos, ir s¹lyga (A) nëra tenkinama. Tikrinsime s¹lyg¹ (B):

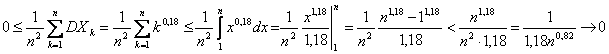kai

S¹lyga (B) yra tenkinama, t.y. pagal Èebišovo teorem¹ sekai galioja didžiøjø skaièiø dësnis.

Kiekvienam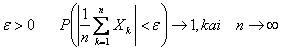

Monte-Karlo metodu apytiksliai apskaièiuokite integral¹ ir ávertinkite absoliutinê paklaid¹. Èia

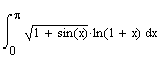
Pažymime integral¹

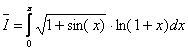
èia

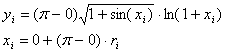
O, r₁,r_n – atsitiktiniai dydžiai tolygiai pasiskirstê intervale (0, 1).

Imkime n = 20. tarpiniai rezultatai pateikti lentelëje.

Iš èia gauname integralo I ávertá:

Sukonstruojame integralo I pasikliautin¹já interval¹. Imame . Turime

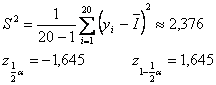
Iš èia gauname integralo I pasikliautin¹já interval¹:

Tai reiškia, kad su tikimybe 0,9 galime, jog integralo I reikšmë yra tarp 2,931 ir 4,065