| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
| Autó | élelmiszer | épület | Földrajz | Gazdaság | Kémia | Marketing | Matematika |
| Oktatás | Orvostudomány | Pszichológia | Sport | Számítógépek | Technika |
DOCUMENTE SIMILARE |
|
Állapotegyenlet
Az előző példák tanulságát a következőkben általánosíthatjuk. Folytonos idejű folyamatok dinamikus viselkedését az állapotváltozók számával azonos elsőrendű differenciálegyenlettel és a kimenő jelek számával azonos algebrai egyenlettel lehet jellemezni. Ezek az állapotegyenletek. Ha az állapotváltozókat x, a bemenő jeleket u, a kimenő jeleket y jelöli, akkor pl. egy két állapotváltozós, három bemenő és egy kimenő jelű lineáris rendszerre az állapotegyenletek az alábbi uniformizált alakban írhatók:
![]()
![]()
![]()
Az a, b, c, d együtthatók a rendszer paraméterei. A bemenő jelek az irányító és a zavaró jelekből állnak.
A skaláris forma a változók számának növekedésével kezelhetetlenné válik. Az áttekinthetőséget vektor változók bevezetésével lehet növelni.
Legyenek X, U, Y olyan oszlopvektorok, amelyeknek skalár rendezői az állapotváltozók, a bemenő jelek ill. a kimenő jelek. Ezekkel a fenti egyenletek mátrixos formában:
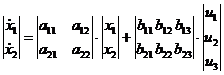
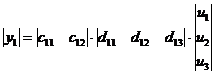
vagy a mátrixokat nagybetűkkel jelölve
![]()
![]()
Az A, B, C, D mátrixokat a rendszer paraméter mátrixainak nevezzük. Az egyenletek megoldásához peremfeltételeket kell rögzíteni. Ezeket a következőkben kezdeti feltételek formájában a t=0 időre vonatkozó X(0) értékkel adjuk meg:
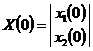
A következőkben a jelölésben nem teszünk különbséget a mátrixok, a sor és az oszlopvektorok között. Valamennyit nagybetűvel jelöljük. A jellegük a definíciójukból következik. X, U, Y oszlopmátrixok, az A mátrix kvadratikus, B, C, D általában nem kvadratikusak.
A bemenő jelek többféleképpen is csoportosíthatók, így a B és D mátrixok is többféleképpen felbonthatók. Ha a példánkban u1 az irányító jel, u2 és u3 a zavaró jel komponensei, -akkor a bemenő vektor
![]() ,
,
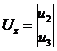
részekre bontható, az állapotegyenlet
![]()
![]()
alakú lesz, ahol Bi ill. Di oszlopmátrixok, Bz és Dz kvadrikus.
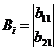
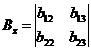
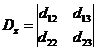
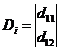
De U-nak mindhárom skaláris komponense is megtartható önálló bemenőjelnek. Ekkor a hozzájuk rendelhető B és D mátrixok értelemszerűen módosulnak.
Az egybemenetű – egy kimenetű (SISO, single input-single output) rendszerekben U=u és Y=y skalárok, B oszlop, C pedig sormátrix, D=d skalár.
A frekvencia tartományba az állapotegyenletek Laplace transzformációval vihetők át. Jelölje az X, U, Y idővektorok transzformáltját X(s), U(s), Y(s).
Figyelembe véve a differenciálhányados transzformálásának a szabályait:
![]()
![]()
Az a egyenletben X(0) olyan bemenő jelnek tekinthető, amely a B0 egységmátrixon keresztül hat a rendszerre, ahol
![]()
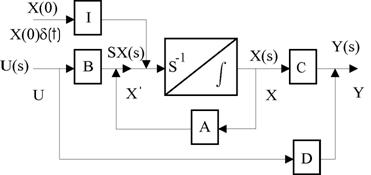
3.4. ábra: A frekvencia tartománybeli állapotdiagram.
A kezdeti értékeket tehát egy speciális bemenő jelként lehet figyelembe venni. Ugyanez az időtartományban is megtehető. A frekvencia tartományban konstans érték az időtartományban Dirac umpulzust jelent. Az állapotegyenlet időtartománybeli megfelelője:
![]()
![]()
Az állapotváltozók mint koordináták egy teret – az állapotteret (state space) – definiálnak. Ebben a térben helyezkedik el az X(t) állapotvektor. Végpontjának elmozdulása jelenti a rendszer mozgását. Az állapotvektor végpontja által leírt görbe az állapottrajektória.
Rendszeranalízis tipikus vizsgáló jelekkel
Az irányítási rendszer analízisének a célja a statikus és a dinamikus tulajdonságok feltárása. Ezek részben a bemenő jeltől, részben a rendszer paramétereitől függnek. A rendszerfüggő dinamika a tranziens mozgáskomponensekben tükröződik.
Minthogy az X(0)=0 kezdeti állapotból induló gerjesztett mozgásban mind a gerjesztő jelnek
megfelelő egyensúlyi állapot, mind a tranziensek megjelennek, általában elegendő ennek vizsgálata. Bemenő jeleknek célszerű olyan jeleket használni, amelyek képesek a vizsgálni kívánt hatást kellő mértékben előidézni, eléggé egyszerűek és az eredményben könnyen elkülöníthetőkké teszik a rendszer és a bemenő jel hatását.
A Dirac impulzus
Csak tanzienseket gerjeszt, a hozzárendelhető egyensúlyi állapot megegyezik a magára hagyott rendszer nyugalmi állapotával. Mivel azonban kisérletileg nem realizálható, sokszor az ugrásfüggvényt használják helyette.
A Dirac impulzus defíniciója:
![]()
A t=0 ppillanatban ható impulzus egységnyi erőségű, azaz
![]()

3.5. ábra: A d(t) függvény
A Dirac impulzus laplace transzformáltja:
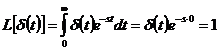
Az egységugrás függvény
Tranzienseket és olyan egyensúlyi állapotot hoz létre, amely csak egy additív konstansban különbözik a magára hagyott rendszer nyugalmi állapotától.
Az egységugrás definiciója a következő:
![]()
Mind a d(t), mind az egységugrás függvény konstanssal szorzott és időben eltolt formában is gyakran használatos.
Az egységugrás függvény Laplace transzformáltja:
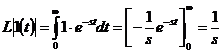
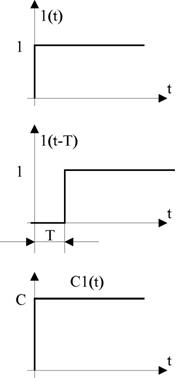
3.6. ábra: Egységugrás függvény
További tipikus vizsgáló jelek az egyoldalas hatványfüggvények és az exponenciális függvények.
A lineáris rendszer mozgása
Az előző pontok alapján a lineáris rendszer mozgási sajátosságait a következőkben foglalhatjuk össze:
A mozgásnak két formája van:
1.) A nyugalmi helyzetéből kimozdított, majd (pl. a t=0 pontban) magára hagyott rendszer mozgása.
2.) A gerjesztett rendszer mozgása, amelyet a nyugalmi helyzetben levő rendszerre adott bemenő jel – gerjesztő jel – vált ki. Az általános mozgásban a két forma szuperponálódik.
A nyugalmi állapotából kitérített, majd magára hagyott rendszer kétféleképpen viselkedhet:
1a) Stabilis rendszer visszatér a nyugalmi helyzetébe, vagy annak a kimozdítás mértékétől függő környezetébe.
1b) Labilis rendszer nem tér vissza a nyugalmi helyzetébe ill. annak a környezetébe.
A gerjesztett rendszer mozgásában két mozgástípus szuperponálódik.
2a) A gerjesztett egyensúlyi mozgás a bemenő jel által kiváltott mozgásnak az a komponense,
amelyik kielégíti az inhomogén egyenletet.
Ha a rendszer pólusai különböznek a bemenő jelétől, ez az összetevő a bemenő jel pólusai szerint változik. Ha közös pólusok is vannak, ez a megkülönböztetés értelmét veszti
2b) Ha a kiindulási (t=0) állapotban a rendszer állapota eltér a gerjesztett egyensúlyi mozgás ugyanezen időpontbeli állapotától, a közöttük levő eltérés kiegyenlítő (tranziens) összetevőt gerjeszt, amely a két állapot különbségéből, mint kezdő állpotból kiindulva a magára hagyott rendszer mozgási törvényszerűsége szerint változik.
A gerjesztett rendszer egyensúlyi állapota így a gerjesztett egyensúlyi mozgásból és a magára hagyott rendszer egyensúlyi állapotából tevődik össze. A stabilis gerjesztett rendszer mozgása ugyanúgy tart e felé, mint ahogyan a magára hagyott rendszer megközelíti saját egyensúlyi állapotát.
Szokásos az is, hogy a tranziens összetevők közé a kiegyenlítő mozgásnak csak a csillapodó komponenseit sorolják. Ekkor úgy kell fogalmazni, hogy a tranziens összetevőt a kiindulási állapotban a gerjesztett rendszernek a tényleges és az egyensúlyi állapota közötti különbség generálja.
Gépi számítások folytonos idejű rendszerekre az időtartományban
A MATLAB az X állpotvektort és a kimenő Y vektort az állapotegyenletekből vagy az átviteli függvényekből számítja, az lsim (linear simulation), impulse, step és az initial utasításokkal.
Az lsim tetszőleges bemenő jelre és kezdeti értékekre használható. Paraméterként vagy az állapotegyenlet paraméter mátrixait, vagy az átviteli függvény számláló és nevező polinomjait kell megadni az azonos lépésközű számítási időpontokkal és az ezen időpntokbeli bemenő jel értékekkel együtt.
Az initial utasítás a magára hagyott rendszer állapotvektorát és kimenő jelét számítja az X(0) kezdeti állapotvektorból kiindulva. Az idővektort automatikusan is képes generálni.
Az impulse ill. a step utasítások Dirac függvény ill. ugrásfüggvény bemenetre számítják az állapotvektort és a kimenő jeleket. Az időpontok vektorait automatikusan is meg tudják állapítani.
Amikor a megadott paraméterek az átviteli függvényre vonatkoznak, a MATLAB a tf2ss (transfer function to state space) utasítással automatikusan előállítja az állapotegyenletet és annak az állapotvektorát számítja ki.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2192
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved