| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
Testy dla wartości oczekiwanej ( średniej)
W stołówce studenckiej przeprowadzono wyrywkową kontrolę masy porcji obiadowej mięsa, która nominalnie powinna wynosić 120g. Losowo wybrano, a następnie zważono 10 porcji, uzyskując następujące wyniki pomiarów ( w gramach): 122, 118, 115, 116, 123, 125, 116, 114, 120, 121. Na poziomie istotności α = 0,05 sprawdzić hipotezę, że studenci w badanej stołówce są żywieni zgodnie z recepturą. Zakłada się, że rozkład masy porcji mięsa w całej populacji jest rozkładem normalnym
Rozwiązanie:
Należy wyznaczyć średnią wagę porcji mięsa oraz odchylenie standardowe
|
|
|
|
stąd: ![]()
hipotezy: ![]()
Dla weryfikacji hipotezy zerowej korzystamy ze statystyki:
![]()
wartość statystyki:
![]()
poziom ufności: 1 - α = 0,95
z tablic rozkładu t Studenta ![]()
Weryfikacja:
ponieważ: ![]() , nie ma podstaw do odrzucenia hipotezy zerowej
, nie ma podstaw do odrzucenia hipotezy zerowej
Testy na równość dwóch wartości przeciętnych
Zaistniało podejrzenie, że pierwsza z 2 obrabiarek pracujących na wydziale mechanicznym dostarcza elementy zawyżonej długości. Wybrano losowo i zmierzono 200 elementów wytworzonych na obrabiarce pierwszej i 100 elementów otrzymanych z drugiej obrabiarki. Po przeprowadzeniu obliczeń uzyskano:
![]()
Na poziomie α = 0,05 zweryfikować hipotezę, ze obie obrabiarki wytwarzają elementy o tej samej długości.
Rozwiązanie:
hipotezy: ![]()
![]()
wykorzystujemy statystykę u o wzorze:
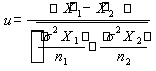
wartość statystyki:
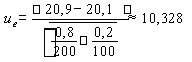
Weryfikacja:
ponieważ: ![]() , hipotezę zerową należy odrzucić na
korzyść hipotezy alternatywnej
, hipotezę zerową należy odrzucić na
korzyść hipotezy alternatywnej
Testy dla wariancji
Pewnego dnia dokonano 15 pomiarów opóźnień pociągów kursujących do stacji Wrocław Główny; otrzymano w minutach: 20, 25, 48, 28, 42, 90, 12, 1, 4, 10, 5, 15, 2, 35, 8. Zakłada się, że czas opóźnień pociągów ma rozkład N(m, (X)). Sprawdzić na poziomie istotności α = 0,05 hipotezę, że wariancja opóźnień wynosi 400.
Rozwiązanie:
hipotezy: ![]()
![]()
wartości parametrów rozkładu z próby:
|
|
|
|
|
|
||
na podstawie tabelki: ![]()
dla weryfikacji hipotezy zerowej wykorzystujemy statystykę chi kwadrat, daną wzorem:
![]()
Z tablic ![]() . Ponieważ zachodzi nierówność
. Ponieważ zachodzi nierówność ![]() nie ma podstaw do odrzucenia hipotezy zerowej.
nie ma podstaw do odrzucenia hipotezy zerowej.
Chcąc polepszyć precyzję
wnioskowania w zagadnieniu z poprzedniego przykładu zwiększono
liczbę pomiarów do 120 w ich wyniku ustalono ![]() na poziomie istotności
na poziomie istotności
α = 0,01 ponownie sprawdzić hipotezę, ze wariancja opóźnień pociągów wynosi 400.
Rozwiązanie:
korzystamy ze statystyki
![]()
obliczając ![]() ze wzoru
ze wzoru ![]() otrzymujemy:
otrzymujemy:
![]()
by uzyskać wartość Ue
![]()
ponieważ ![]() hipotezę zerową należy odrzucić na
korzyść hipotezy alternatywnej.
hipotezę zerową należy odrzucić na
korzyść hipotezy alternatywnej.
Test zgodności χ2 ( chi kwadrat)
Wyłoniono próbę losową złożoną z 400 czteroosobowych, w których odnotowano roczne wydatki na turystykę i rekreację przypadające na członka rodziny. Na poziomie α = 0,05 zweryfikować hipotezę, że rozkład wydatków na turystykę i rekreację jest rozkładem normalnym.
|
Wydatki |
Liczba rodzin |
Rozwiązanie:
formułujemy hipotezę zerową ![]() oraz alternatywną:
oraz alternatywną: ![]()
Wyznaczamy wartość estymatorów z
próby: ![]()
rozkład empiryczny porównujemy z rozkładem teoretycznym przez zastosowanie statystyki:
![]()
tablica pomocna przy wyliczeniu wartości statystyki
uwaga: każdy z przedziałów wydatków jest reprezentowany przez górną jego granicę
|
|
|
|
|
|
|
|
|
x |
x |
x |
x |
|
z tablicy rozkładu χ2 odczytujemy
krytyczną wartość: ![]()
ponieważ: ![]() nie ma podstaw do odrzucenie hipotezy zerowej.
nie ma podstaw do odrzucenie hipotezy zerowej.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3829
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved