| CATEGORII DOCUMENTE |
| Bulgara | Ceha slovaca | Croata | Engleza | Estona | Finlandeza | Franceza |
| Germana | Italiana | Letona | Lituaniana | Maghiara | Olandeza | Poloneza |
| Sarba | Slovena | Spaniola | Suedeza | Turca | Ucraineana |
DOCUMENTE SIMILARE |
|
CONVERTIR UN AFN EN AFD
1. Equivalencia entre autómatas Equivalencia entre AFD y AFN
La equivalencia entre AFD y AFN es clara entendiendo todo AFD como un caso particular de un AFN. En el otro sentido, a partir un AFN A=(Q,S, d,q0,F) se puede construir otro AFD A'=(Q',S, d', q0', F') equivalente (que acepte el mismo lenguaje), de la siguiente forma:
Figura 1. Autómata finito no determinista del ejemplo 1.
Ejemplo 1. Dado el
autómata de la figura 1, el proceso de construcción de un AFD equivalente parte
del estado inicial , y determina el conjunto de estados
alcanzables con cada símbolo del alfabeto. De esta forma, por ejemplo, al
considerar el símbolo a se alcanzan los estados .
Cada uno de los conjuntos de estados que aparezcan se considera como uno de los
estados del AFD equivalente, determinandose para cada uno de ellos su función
de transición. El proceso se repite mientras aparezcan nuevos estados. La
figura 2 muestra la tabla de transiciones del AFD.
|
a |
b |
c |
|
|
Æ | |||
|
Æ |
Æ | ||
Figura 2. Tabla
de transiciones del AFD equivalente al AFN de la
a partir de esta tabla el diagrama de transiciones queda como muestra la figura
Figura Autómata finito determinista equivalente.
Ejemplo 2. Dado el AFN de la figura 4 la tabla de transiciones del AFD equivalente sería la mostrada en la figura 5, con lo que el diagrama de transiciones del AFD quedaria como se muestra en la figura 6
Figura 4. AFN ejemplo.
|
a |
b | ||
Figura 5. Tabla de transiciones
del AFD equivalente al AFN de la figura 4.
![]()
Figura 6. AFD equivalente al AFN
de la figura.
El estado es el único estado final
del AFD porque es el único que contiene el estado q2, estado final
del AFN original.
Equivalencia entre AFD y AFl
A partir de todo autómata finito no determinista con l-transiciones A=(Q,S, d,q0,F), se puede construir un AFD equivalente. Para ello seguiremos los siguientes pasos:
1. Obtener un AFN A'=(Q,S,d', q0, F') donde:
τ(q,l) = l-clausura(q)
τ(q,xa) = l-clausura È(p I
τ(q,x)) d(p,a)
de esta forma A' no posee l-transiciones.
Figura 7. Ejemplo de autómata finito con transiciones vacias
Ejemplo Dado el AFl de la figura 7, representamos en la figura 8 su tabla de transiciones y la l-clausura de cada estado.
|
a |
b |
l-clausura |
|
|
q0 |
Æ | ||
|
q1 | |||
|
q2 | |||
|
q3 |
Æ |
Æ | |
Figura 8. Tabla de transiciones
y l-clausura de cada estado del AFl de la figura 7.
Para obtener el conjunto de transiciones del AFN equivalente aplicaremos la
construcción indicada al principio de la sección. Por ejemplo, para obtener el
conjunto de transiciones del estado q0 con el símbolo b en el
AFN equivalente:
Procediendo de igual forma para todo q I Q y todo a I S, obtenemos la tabla de
transiciones del AFN sin transiciones vacias que se muestra en la figura 9. En
este AFN, el único estado final es q3 porque l-clausura(q0)
Ç F = Æ. Una vez obtenida la tabla de transiciones del AFN, se puede
construir el AFD equivalente que queda como muestra la figura 10.
|
a |
b | ||
|
q0 |
| ||
|
q1 | |||
|
q2 | |||
|
q3 | |||
Figura 9. Tabla de transiciones
del AFN equivalente al AFl de la figura 7.
Figura 10. Autómata finito
determinista equivalente al AFl de la figura 7.
Ejemplo 4. Otro ejemplo de AFl es el mostrado en la figura 11.
Figura 11. Autómata finito con transiciones vacías.
La tabla de transiciones y la l-clausura de cada estado del autómata de la
figura 11 se muestran en la figura 12.
|
l-clausura |
|||
|
q0 |
Æ | ||
|
q1 |
Æ | ||
|
q2 | |||
|
q3 |
Æ | ||
Figura 12. Tabla de transiciones
y l-clausura de cada estado en el AFl de la figura 11.
Como ejemplo del paso a AFN, para obtener el conjunto de transiciones del
estado q1 con el símbolo a:
El AFN resultado tiene como estados finales porque en este caso l-clausura(q0) Ç F ¹ Æ. Al repetir el proceso para cada estado se obtiene la tabla de transiciones de la figura 1 A partir de ella, se puede obtener el AFD de la figura 14.
|
q0 | |||
|
q1 |
Æ | ||
|
q2 | |||
|
q3 |
Æ | ||
Figura 1 Tabla de transiciones del AFN equivalente al AFl de la
Figura 14.Autómata finito determinista equivalente al AFl de la 11
ELABORANDO UN AFD
La construcción de AFD’s es esencial para entender el comportamiento de las expresiones regulares. Dado un alfabeto y una serie de condiciones, se puede elaborar un AFD que satisfaga dichas condiciones, mediante ensayo y error
Ejercicios
Dado el alfabeto en , elaborar un AFD que acepte solamente palabras
que empiecen con 00
que no empiecen con 00
con un número par de ceros
con un número impar de unos
con las dos condiciones anteriores
A continuación se realiza el inciso c:
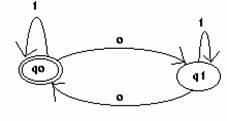
Las palabras reconocidas son todas aquellas que llegan a los estados finales a partir del estado inicial. Un autómata finito (determinista) es pues una estructura de la forma
![]()
donde

Un semiautómata finito es una estructura de la forma
![]()
Es
decir, es un ``autómata finito'' en el que no se ha especificado estados
finales. Todo autómata finito puede ser visto como un semiautómata con estados
finales distinguidos. El semiautómata determinado por un autómata se dice ser
el semiautómata subyacente
del autómata. Todas las nociones y aseveraciones hechas sobre semiautómatas
serán válidas también en los autómatas de los que son subyacentes. Como en las
máquinas finitas, ya sea de Mealy o de Moore, en cada semiautómata extendemos
la función de transición ![]() a
una función
a
una función ![]() ,
haciendo, para cada estado
,
haciendo, para cada estado ![]() :
:
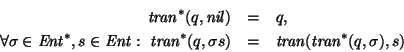
Sea ![]() la
función
la
función ![]() .
Un estado
.
Un estado ![]() se
dice ser accesible si
está en la imagen de T, es decir, si
se
dice ser accesible si
está en la imagen de T, es decir, si ![]() .
La parte accesible de
.
La parte accesible de
![]() es la imagen de T, es decir, consta de
todos los estados accesibles a partir del estado inicial.
es la imagen de T, es decir, consta de
todos los estados accesibles a partir del estado inicial.
Lema 2.1 Sea ![]() un
semiautómata finito. Cualquier estado accesible se alcanza mediante una palabra
de longitud a lo sumo el número total de estados,
un
semiautómata finito. Cualquier estado accesible se alcanza mediante una palabra
de longitud a lo sumo el número total de estados, ![]() . En otras palabras, la parte accesible del
semiautómata coincide con el conjunto
. En otras palabras, la parte accesible del
semiautómata coincide con el conjunto ![]()
En
efecto, para cada ![]() sea
sea
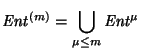 el conjunto de palabras de longitud a lo sumo
m. La colección de conjuntos es un recubrimiento (creciente) del
diccionario
el conjunto de palabras de longitud a lo sumo
m. La colección de conjuntos es un recubrimiento (creciente) del
diccionario ![]() mediante conjuntos anidados:
mediante conjuntos anidados:
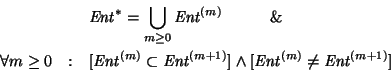
Consecuentemente, ![]() es
también un recubrimiento de Q mediante conjuntos anidados. Por ser Q
finito, necesariamente para algún índice m0 se ha de tener
que
es
también un recubrimiento de Q mediante conjuntos anidados. Por ser Q
finito, necesariamente para algún índice m0 se ha de tener
que ![]() ,
y, de hecho, para todo
,
y, de hecho, para todo ![]() ,
,
![]() .
Así pues, se tiene una cadena finita de inclusiones,
.
Así pues, se tiene una cadena finita de inclusiones,
![]()
Como
cualesquiera dos conjuntos consecutivos ![]() ,
, ![]() pueden
diferir en al menos un elemento en Q se tiene que
pueden
diferir en al menos un elemento en Q se tiene que ![]() .
Además,
.
Además, ![]() .
De aquí se sigue la tesis del lema, quod
erat demonstratum (q.e.d.).
.
De aquí se sigue la tesis del lema, quod
erat demonstratum (q.e.d.).
La parte accesible, ![]() ,
de un semiautómata
,
de un semiautómata ![]() consta de todos sus estados accesibles.
Naturalmente, se tiene un algoritmo elemental para construir la parte accesible
de cualquier semiautómata finito:
consta de todos sus estados accesibles.
Naturalmente, se tiene un algoritmo elemental para construir la parte accesible
de cualquier semiautómata finito:
1. Consideremos dos listas: una de estados ya revisados y otra de estados por revisar. Inicialmente la primera está vacía y la segunda consta sólo del estado inicial.
2. Para cada estado por revisar,
(a) se toma a ese estado como actual q,
(b)
para cada símbolo de entrada ![]() sea
sea ![]() . Si p
aparece en alguna de las dos listas se pasa al siguiente símbolo, en otro caso
se lo coloca al final de los estados a revisar,
. Si p
aparece en alguna de las dos listas se pasa al siguiente símbolo, en otro caso
se lo coloca al final de los estados a revisar,
(c) se coloca el estado actual en la lista de los ya revisados.
En la figura 5 se presenta un pseudo código de este algoritmo.
|
Figure 5: Cálculo de la parte accesible. |
|
|
El lema anterior implica que el número de iteraciones en el ciclo principal del
algoritmo anterior no excede al número de estados en el autómata.
Ejemplo. Si ![]() consta de un único símbolo entonces el
algoritmo 5 muestra que la parte accesible tiene forma de la letra griega
``rho'',
consta de un único símbolo entonces el
algoritmo 5 muestra que la parte accesible tiene forma de la letra griega
``rho'', ![]() ,
es decir, existen
,
es decir, existen ![]() tales
que
tales
que
Sea ![]() un
autómata finito. Decimos que una palabra
un
autómata finito. Decimos que una palabra ![]() es reconocida por A si
es reconocida por A si ![]() , es decir,
, es decir, ![]() es
reconocida si al aplicarla a
es
reconocida si al aplicarla a ![]() desde el estado inicial se arriba a uno de
los estados finales. El lenguaje
reconocido por
desde el estado inicial se arriba a uno de
los estados finales. El lenguaje
reconocido por ![]() consta de todas las palabras reconocidas por
consta de todas las palabras reconocidas por ![]() :
:
![]()
Diremos que un autómata ![]() subsume
a otro autómata
subsume
a otro autómata ![]() si
si ![]() .
La relación de ``subsunción'' es reflexiva y transitiva. Diremos que dos
autómatas son equivalentes
si uno subsume al otro, es decir, si coinciden los lenguajes reconocidos por
ellos. Esta es una relación de equivalencia entre autómatas. Diremos que un
lenguaje
.
La relación de ``subsunción'' es reflexiva y transitiva. Diremos que dos
autómatas son equivalentes
si uno subsume al otro, es decir, si coinciden los lenguajes reconocidos por
ellos. Esta es una relación de equivalencia entre autómatas. Diremos que un
lenguaje ![]() es regular-AF si existe un
autómata finito
es regular-AF si existe un
autómata finito ![]() tal que
tal que ![]() .
.
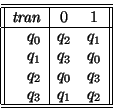
Ejemplos. Sea ![]() . 1.
Construyamos un autómata que reconozca cadenas binarias con números pares de
0's y de 1's. Consideremos los estados siguientes:
. 1.
Construyamos un autómata que reconozca cadenas binarias con números pares de
0's y de 1's. Consideremos los estados siguientes:

La tabla de transición queda definida de manera natural:
El
estado inicial es q0 y el conjunto de estados finales es ![]() .
Es fácil ver que el lenguaje reconocido por este autómata es
.
Es fácil ver que el lenguaje reconocido por este autómata es
![]()
El
lenguaje L es pues regular-AF. En este ejemplo, es también muy fácil ver
que para cada ![]() ,
, ![]() queda
determinada por las paridades de 0's y de 1's en
queda
determinada por las paridades de 0's y de 1's en ![]() .
.
2. Consideremos el autómata con tabla de transición
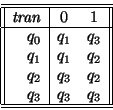
y estado inicial q0. Observemos que
si se arriba al estado q3 ya no se sale de ahí,
se arriba a q3 si inicialmente aparece un 1 y no hay 0's que lo precedan, o bien, habiendo llegado un bloque de 0's y luego uno de 1's, reaparece un 0.
Así
pues, si el conjunto de estados finales es ![]() entonces
el lenguaje reconocido por este autómata es
entonces
el lenguaje reconocido por este autómata es ![]()
AUTÓMATAS FINITOS NO DETERMINISTAS
CONVERTIR UN DIAGRAMA NO DETERMINISTA EN UNO DETERMINISTA
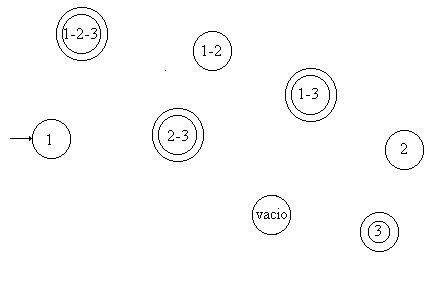
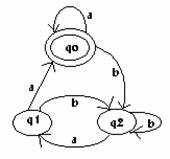
Cojamos el diagrama del siguiente autómata para el alfabeto S =. Como podemos ver, no es determinista pues desde el estado 1 salen dos arcos rotulados con b y del estado 2 salen dos arcos etiquetados con a.
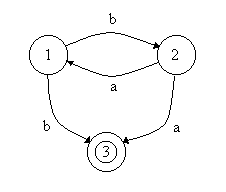 <>
<>
Para convertir el diagrama no determinista en uno que lo sea vamos ha realizar los siguientes pasos:
S'=P(S)
Conjunto de todos los subconjuntos de S (recordar que el conjunto potencia se
encuentra incluido el conjunto vacío, que será el estado de captación global)
Como tenemos tres estados, el conjunto potencia
P(S) =
i'=
(mismo estado inicial)
En nuestro caso seguirá siendo el estado 1.
F'
es la colección de subconjuntos de S (estados de S') que contienen, por lo
menos, un estado de F (cada uno de los estados de S' dentro de los cuales hay
al menos un estado de aceptación de M).
En nuestro caso serán todos los subconjuntos que
tengan el estado 3, ya que este es el único estado de aceptación del diagrama
original; luego F'=
d es
la función de S' x S a S'; Para cada símbolo del alfabeto y estado s' de S', d
(s',x) es el estado de S' compuesto por los estados de S a los que es posible
llegar desde todos los estados s de s' siguiendo un arco con etiqueta x. Como d
es una función, M' es finito determinista.
En nuestro caso, En cada estado del conjunto
potencia solo va a salir un arco por cada símbolo, siendo el destino, el estado
de S' que tenga todos los estados a los que fuera en el diagrama inicial: para
ello:
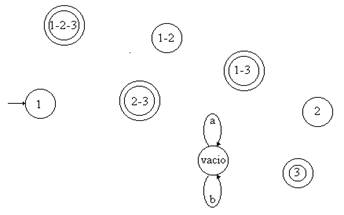
+ vacío.- como dijimos, era el estado de captación global, por lo tanto
se le dibujan tantos arcos que salen e inciden en el estado, como símbolos del
alfabeto haya, con los cuales se rotulan. Además, en este estado, van a incidir
todas aquellas transiciones que no existían para algún símbolo en algún estado
original.
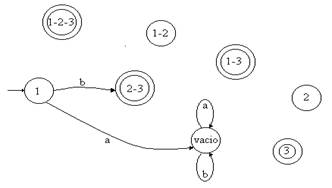
* Estado 1.- Con la etiqueta a no hay transición en el original, por lo tanto el arco se dibuja hacia el estado vacío con la etiqueta b salen dos arcos, uno hacia el estado 2 y otro al estado 3, por lo tanto el arco se dibuja al estado 2-3
*
Estado 2.- Con la etiqueta b no hay transición en el original, por lo tanto el
arco se dibuja hacia el estado vacío; con la etiqueta a salen dos arcos, uno
hacia el estado 1 y otro al estado 3, por lo tanto el arco se dibuja al estado
1-
* Estado - Con ninguna de las dos etiquetas hay transición en el original, por
lo tanto se dibujan sendos arcos hacia el estado vacío.
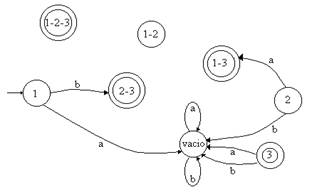
*
Estado 1-2.- Con la etiqueta a hay transición desde el estado 2 original al 1 y
3 original, por lo tanto el arco se dibuja hacia el estado 1-3; con la etiqueta
b salen dos arcos desde el estado 1 original, uno hacia el estado 2 y otro al
estado 3, por lo tanto el arco se dibuja al estado 2-
* Estado 1-- Con la etiqueta a no hay transición desde ninguno de los dos
estados originales, por lo tanto el arco se dibuja hacia el estado vacío; con
la etiqueta b salen dos arcos desde el estado 1 original, uno hacia el estado 2
y otro al estado 3, por lo tanto el arco se dibuja al estado 2-
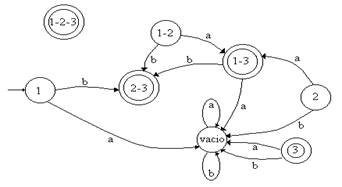
*Estado
2-- Con la etiqueta a hay transición desde el estado 2 original al 1 y 3
original, por lo tanto el arco se dibuja hacia el estado 1-3; con la etiqueta b
no sale ningún arco en ninguno de los dos estados originales, por lo tanto el
arco se dibuja al estado vacío.
* Estado 1-2-- Con la etiqueta a hay transición desde el estado 2 original al 1
y 3 original, por lo tanto el arco se dibuja hacia el estado 1-3; con la
etiqueta b salen dos arcos desde el estado 1 original, uno hacia el estado 2 y
otro al estado 3, por lo tanto el arco se dibuja al estado 2-
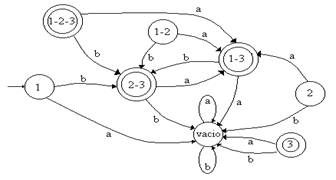
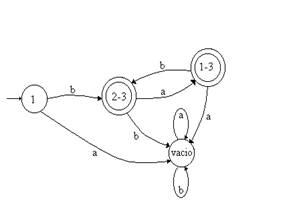
Una
vez que hemos terminado todos los pasos, podremos eliminar aquellos estados que
sean superfluos al diagrama que acabamos de obtener.
En nuestro caso particular podemos eliminar los
estados 2, 3, 1-2 y 1-2-3, quedando el definitivo autómata finito determinista.
TEOREMA DE TRANSFORMACIÓN AFN A AFD
Para todo AFN N existe algún AFD D tal que L(N)=L(D)
Un AFN con transiciones e puede ser convertido en un AFN sin transiciones e, eliminando las transiciones vacías, sin alterar el comportamiento del autómata. Para hacer esto, es necesario comprender que las deltas manejadas tienen una diferencia cuando se trata de la cerradura al vacío, ya que en el AFN sin e la cerradura al vacío de un estado es solamente el mismo estado.
Lema. Para cada x,y I S y A K, D(A,xy) = D D(A,x),y)
El lema anterior nos dice que es posible separar las cadenas en una operación de transición de un Autómata Finito. Esta separación nos ayudará a simplificar el rastreo de la cadena general.
Ejercicios.
Obtener un AF que acepte ((a+b)(a+b))*(ab+(ba)*)
Obtener una ER para el lenguaje generado por el siguiente autómata:
En este capítulo se enseÑó el concepto de Expresión Regular y su relación para ser representado por un Autómata Finito. La construcción de AF’s tiene como base los grafos de transición, los cuales nos muestran cómo un lenguaje puede ser reconocido por dicho grafo.
NOCIONES BÁSICAS
Los autómatas no-deterministas se conforman como los autómatas finitos ya vistos, salvo que sus transiciones, en lugar de ser funciones, son relaciones que a cada pareja (estado, estímulo) le asocian varios, uno o ningún estado. Más precisamente: Un semiautómata no-determinista es una estructura de la forma
![]() donde
donde

Un autómata no-determinista
es una pareja ![]() donde
SAFND es un
semiautómata no-determinista y
donde
SAFND es un
semiautómata no-determinista y ![]() es
un conjunto de estados finales.
Si
es
un conjunto de estados finales.
Si ![]() decimos
que se puede transitar
a p desde el estado q cuando arriba un símbolo e. Para
cada pareja
decimos
que se puede transitar
a p desde el estado q cuando arriba un símbolo e. Para
cada pareja ![]() su imagen bajo la transición es el
conjunto
su imagen bajo la transición es el
conjunto ![]() , es decir, es el conjunto de estados a los
que se puede transitar desde q con e. De manera reiterada, para
, es decir, es el conjunto de estados a los
que se puede transitar desde q con e. De manera reiterada, para ![]() ,
definimos la imagen
,
definimos la imagen ![]() como
sigue:
como
sigue:
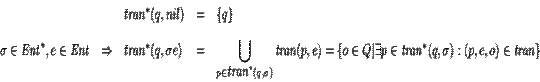
Para
cada ![]() definimos
definimos
![]() .
Una palabra
.
Una palabra ![]() es reconocida por el autómata
es reconocida por el autómata ![]() si algún estado en
si algún estado en ![]() es
final. El lenguaje
del autómata
es
final. El lenguaje
del autómata ![]() consiste de todas las palabras que reconoce,
consiste de todas las palabras que reconoce, ![]()
Ejemplo. Sea ![]() el
autómata no-determinista tal que
el
autómata no-determinista tal que
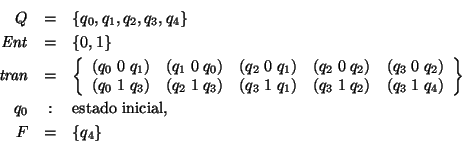
En la siguiente tabla presentamos el cálculo de la correspondiente función T
en algunas palabras:
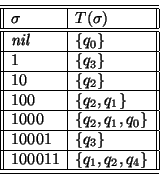
Así
pues, ![]() y
consecuentemente
y
consecuentemente ![]() .
.
Observación 1 Todo autómata finito (determinista) es también un autómata finito no-determinista.
En efecto, las funciones son casos particulares de relaciones. Por tanto, toda función de transición, es una relación de transición
Representación de transiciones mediante matrices booleanas
Sea ![]() el álgebra
booleana de dos elementos, dotada de sus operaciones usuales de conjunción, ``
el álgebra
booleana de dos elementos, dotada de sus operaciones usuales de conjunción, ``![]() ''
y disyunción, ``
''
y disyunción, ``![]() '':
'':
![]() es
1 sólo si ambos x e y son 1;
es
1 sólo si ambos x e y son 1; ![]() es
0 sólo si ambos x e y son 0. Para cada símbolo de entrada
es
0 sólo si ambos x e y son 0. Para cada símbolo de entrada ![]() definamos la matriz
definamos la matriz ![]() tal que para todos
tal que para todos ![]() :
:
![]()
Similarmente,
para ![]() definamos
la matriz
definamos
la matriz ![]() tal que para todos
tal que para todos ![]() :
:
![]()
Así
pues, ![]() se
tiene la relación,
se
tiene la relación,
![]()
Ahora
bien, la colección ![]() de
matrices booleanas con índices en Q tiene una estructura de anillo con
la operación suma dada por la disyunción entrada a entrada,
de
matrices booleanas con índices en Q tiene una estructura de anillo con
la operación suma dada por la disyunción entrada a entrada,
![]()
y el producto booleano de matrices,
![]()
Lema 1 Si ![]() entonces
entonces ![]() . En particular, si
. En particular, si ![]() entonces
entonces
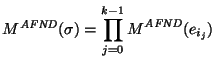 .
.
Ejemplo. Para el AFND del ejemplo anterior
tenemos
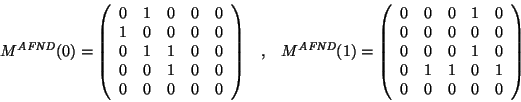
Indeterminismo y determinismo
Diremos
que un lenguaje ![]() es regular-N si coincide con el lenguaje
reconocido por algún autómata no-determinista. Ya que todo autómata finito es
en sí mismo un autómata no-determinista se tiene que todo lenguaje regular es
también un lenguaje regular-N. El recíproco también es cierto.
es regular-N si coincide con el lenguaje
reconocido por algún autómata no-determinista. Ya que todo autómata finito es
en sí mismo un autómata no-determinista se tiene que todo lenguaje regular es
también un lenguaje regular-N. El recíproco también es cierto.
Lema 2 (Equivalencia de determinismo e
indeterminismo) Todo lenguaje regular-N es regular. Es decir, para todo
autómata no-determinista ![]() existe un autómata finito
existe un autómata finito ![]() tal que
tal que ![]() .
.
En
efecto, sea ![]() un autómata no-determinista. Podemos
presentar dos construcciones de autómatas finitos equivalentes a
un autómata no-determinista. Podemos
presentar dos construcciones de autómatas finitos equivalentes a ![]() .
.
Primera construcción. Construyamos el monoide ![]() del
autómata no-determinista
del
autómata no-determinista ![]() y consideremos su estructura de autómata
finito: cada uno de sus elementos
y consideremos su estructura de autómata
finito: cada uno de sus elementos ![]() es
un estado, para cada símbolo
es
un estado, para cada símbolo ![]() definamos la transición
definamos la transición 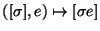 y
definamos como estados finales a las clases de equivalencia
y
definamos como estados finales a las clases de equivalencia ![]() tales
que
tales
que ![]() . Una
palabra será reconocida en este último autómata cuando y sólo cuando lo sea por
. Una
palabra será reconocida en este último autómata cuando y sólo cuando lo sea por
![]() .
.
Segunda construcción. Construyamos el autómata finito ![]() como sigue:
como sigue:
estados:
Todo
subconjunto de estados ``viejos'' será un ``nuevo'' estado, ![]()
transición:
Todo
subconjunto de estados ``viejos'' se transforma en su imagen bajo la función de
transición ``vieja'', 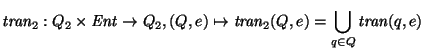 , es decir, para cada
, es decir, para cada ![]() ,
,
![]() si y
sólo si
si y
sólo si ![]() .
.
estado inicial:
Hagamos
![]() , la mónada que consta sólo del estado
inicial ``viejo''.
, la mónada que consta sólo del estado
inicial ``viejo''.
estados finales:
Todo
subconjunto de estados ``viejos'' que contenga alguno final de ésos será un
nuevo estado final: ![]()
Observamos
que rige cada una de las siguientes equivalencias para cualquier palabra ![]() :
:
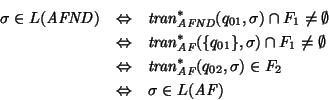
así pues, ![]() y
y ![]() son equivalentes. Observemos también aquí que
el nuevo conjunto de estados ha de tener 2n elementos, donde n
es el número de estados ``viejos''. Esto hace crecer mucho el tamaÑo del
autómata finito equivalente construído de esta forma. Bien que en algunos casos
tal cota superior al número de estados nuevos puede alcanzarse, en muchos otros
casos la parte accesible del autómata construído incluirá sólo una cantidad
mucho menor de estados. Por tanto, en la práctica es muy conveniente construir
tan solo la parte accesible del autómata
son equivalentes. Observemos también aquí que
el nuevo conjunto de estados ha de tener 2n elementos, donde n
es el número de estados ``viejos''. Esto hace crecer mucho el tamaÑo del
autómata finito equivalente construído de esta forma. Bien que en algunos casos
tal cota superior al número de estados nuevos puede alcanzarse, en muchos otros
casos la parte accesible del autómata construído incluirá sólo una cantidad
mucho menor de estados. Por tanto, en la práctica es muy conveniente construir
tan solo la parte accesible del autómata ![]() siguiendo la estrategia del algoritmo (5)
de cálculo de estados accesibles.
siguiendo la estrategia del algoritmo (5)
de cálculo de estados accesibles.
Ejemplo. Consideremos el mismo
ejemplo tratado en esta sección. Cada subconjunto Q del conjunto de
estados ![]() puede ser
codificado por una cadena de 5 caracteres
puede ser
codificado por una cadena de 5 caracteres ![]() de
manera evidente,
de
manera evidente,
![]()
y
cada una de tales cadenas puede ser vista como la representación binaria de un
número entero entre 0 y 31. Nombremos pues con números de ![]() y ``16'', 16=(10000)2, es el nuevo
estado inicial
y ``16'', 16=(10000)2, es el nuevo
estado inicial ![]() . Los nuevos estados finales son todos
aquellos que contegan a q4, es decir, que tengan el último
bit ``prendido''. Los nuevos estados finales son entonces todos los números
impares. Con ayuda de la tabla (14), se ve que la función de transición
del nuevo autómata es la mostrada en la tabla (15).
. Los nuevos estados finales son todos
aquellos que contegan a q4, es decir, que tengan el último
bit ``prendido''. Los nuevos estados finales son entonces todos los números
impares. Con ayuda de la tabla (14), se ve que la función de transición
del nuevo autómata es la mostrada en la tabla (15).
|
Table 15: Transición en el autómata finito equivalente al no-determinista. |
|
|
Observamos en este ejemplo que hay muchos estados inaccesibles tan sólo por el
hecho de que la imagen de la función de transición no incluye a todos los
estados. Con el estímulo 0 sólo se puede arribar a los estados 0, 4, 8, 12, 16,
20, 24 y 28. Con el estímulo 1 sólo se puede arribar a los estados 0, 2, 13 y
15. Si se aplica el algoritmo (5) se obtiene el autómata de 8 estados cuya
tabla de transición es la siguiente:
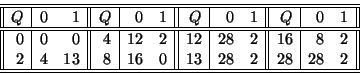
en el que ``16'' es el estado inicial y ``13'' es el único estado final.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 6357
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved