CUADRIPOLUL DIPORT. FILTRE DE FRECVENTA

CUADRIPOLUL DIPORT. FILTRE DE FRECVENta

1 Cuadripolul diport

1.1 Cuadripolul

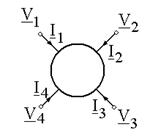Cuadripolul electric este un circuit cu patru borne de acces (fig. 1). Dintre cele patru potentiale complexe, unul se considera origine de potential (), iar cei patru curenti sunt legati prin prima teorema a lui Kichhoff:

,

astfel ca, de la inceput, doar sase marimi complexe (potentiale si curenti) caracterizeaza functionarea cuadripolului.

1.2 Cuadripolul diport Fig. 1

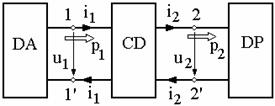La realizarea practica a circuitelor electrice, intre dipolul activ DA (sursa) si dipolul pasiv DP (receptor) din figura 3.7a, se intercaleaza frecvent cuadripolul CD (fig.2.). Acesta poate fi linia bifilara cu parametri care nu se pot neglija, transformator ridicator sau coborator de tensiune, transformator de adaptare, redresor sau invertor, filtru de frecventa. Fig. 2

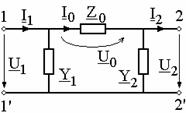
Cuadripolul CD este un diport, avand bornele grupate cate doua in porti: poarta de intrare 1-1' este receptoare, iar poarta de iesire 2-2' este generatoare, in raport cu sensul transferului puterii. Bornele aceleiasi porti sunt traversate de acelasi curent (in sensuri contrare).

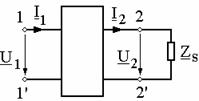Tensiunile si curentii de intrare, respectiv iesire (fig. 3), sunt legate prin sistem Kirchhoff corespunzand structurii cuadripolului. Pentru cuadripolul liniar si pasiv, relatiile dintre cele patru marimi pot fi exprimate prin sistemul:

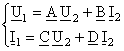, (1) Fig. 3

unde parametrii fundamentali sunt marimi complexe si depind de structura diportului, dar si de frecventa.

In figura 3, la poarta de iesire s-a conectat impedanta de sarcina . In cazul limita cand , cuadripolul functioneaza in scurtcircuit si are . Daca (bornele 2 si 2' libere), cuadripolul este in gol, iar .

Cu aceste precizari, parametrii fundamentali primesc interpretari mai concrete. Primul este raportul de transformare al tensiunilor la mers in gol:

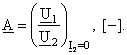(2)

Analog, urmatorii sunt impedanta complexa de transfer in scurtcircuit, admitanta de transfer in gol, respectiv raport de transformare al curentilor in scurtcircuit:

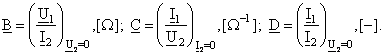
Sistemul (1) se poate scrie evidentiind o matrice [A] a parametrilor fundamentali:

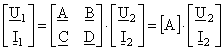. (3)

1.3 Conditia de reciprocitate

Potrivit teoremei reciprocitatii, in cazul cuadripolului diport liniar pasiv, curentul la poarta de iesire scurtcircuitata (fig. 4a), unica sursa fiind situata la poarta de intrare, e egal cu curentul la poarta de intrare scurtcircuitata (fig. 4b), aceeasi sursa E fiind la poarta de iesire.

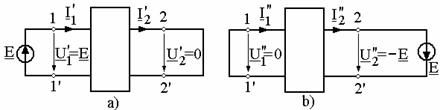
Fig. 4

Se aplica sistemul (1) celor doua situatii:

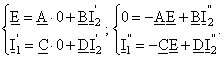
Conditia , valabila pentru orice E, conduce la relatia de reciprocitate:

, (4)

care face ca, in cazul dipolilor liniari, pasivi si reciproci, dintre cei trei parametri fundamentali, doar trei sa fie independenti.

1.4 Alimentarea inversa a diportului

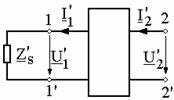
Poarta de iesire devine poarta de intrare si invers, ca in figura

Rezolvarea sistemului (1), in conditiile in care determinantul sau e unitar (4), duce la:

Fig. 5

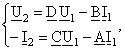
dar in figura 5 s-au facut, in raport cu figura 3, modificari:

Astfel, sistemul de mai sus devine:

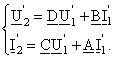(5)

Diportul simetric se comporta identic la alimentarea inversa ca si la alimentarea directa. Pentru aceasta, sistemele (5) si (1) trebuie sa fie similare. Conditia de simetrie este deci:

. (6)

1. Determinarea experimentala a parametrilor diportului

Determinarea experimentala a parametrilor diportului imagineaza o "cutie neagra" la care exista acces doar la cele doua porti. Cu totul impropriu, in literatura de specialitate, masuratorile efectuate cu scopul determinarii parametrilor se numesc uneori incercarile cuadripolilor.

a) Alimentarea directa (fig. 3) cu o tensiune , atunci cand poarta de iesire este in gol (), permite masurarea unui curent de mers in gol , iar sistemul (1) conduce la:

astfel ca se poate exprima impedanta de intrare directa la mers in gol:

(7)

(Este evident ca daca la poarta de iesire, in loc de mers in gol se monteaza un voltmetru, care oricum are o impedanta foarte mare, se masoara , astfel ca rezulta imediat: )

b) Alimentarea directa cu o tensiune , atunci cand poarta de iesire e in scurtcircuit (), permite masurarea unui curent :

rezultand impedanta de intrare la mers in scurtcircuit:

(8)

Observatii. Scurtcircuitul portii de iesire cand la intrare ar fi aplicata tensiunea nominala, la un transformator spre exemplu, e periculos si poate duce la distrugerea instalatiei. La incercarea in scurtcircuit, se aplica la intrare o tensiune redusa printr-un autotransformator, care se mareste numai pana cand curentul absorbit la intrare e cel nominal . Tensiunea aplicata se numeste tensiune de scurtcircuit si se exprima in procente din tensiunea nominala .

La incercarea directa in gol se aplica tensiunea , dar se absoarbe un curent de mers in gol , mult mai mic decat .

Se mentioneaza ca, la incercarile practice ale cuadripolilor, poarta de intrare poate fi echipata si cu wattmetru, care masoara pierderile cuadripolului in gol, respectiv scurtcircuit, caci in ambele cazuri puterea transmisa la iesire e nula.

c) Alimentarea inversa (fig. 5) cu o tensiune , atunci cand poarta de intrare e in gol (), permite masurarea curentului , iar sistemul (5) devine:

si se poate exprima impedanta de intrare inversa la mers in gol:

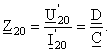(9)

Alimentarea inversa in scurtcircuit se poate face pentru verificare, caci cei patru parametri fundamentali se afla din relatiile (7)-(9) la care se ataseaza, in cazul cuadripolului reciproc, relatia (4).

La cuadripolul simetric sunt suficiente doua incercari, caci se cunoaste conditia (6).

1.6 Scheme echivalente

Daca la paragraful precedent era dat un cuadripol diport (cutie neagra) si se cerea aflarea parametrilor fundamentali, acum se pune problema inversa, de sinteza (proiectare): dandu-se cei patru parametri, se 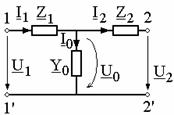cere realizarea unei scheme care sa reproduca functional acea "cutie neagra".

Dintre cei patru parametri fundamentali, la diportul reciproc doar trei sunt independenti, caci a aparut conditia (4). Realizarea fizica e deci posibila cu minimum trei impedante/admitante complexe.

Fig. 6

a) Schema echivalenta in T, prezentata in figura 6, are intre marimi relatiile:

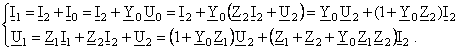
Prin identificare cu sistemul (1), rezulta parametrii fundamentali, iar apoi componentele schemei:

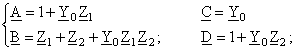(10)

Parametrii verifica relatia de reciprocitate (4). Cuadripolul simetric are (6), deci .

b) Schema echivalenta in (fig. 7) e forma duala a schemei in T, tot rationamentul decurgand prin relatii duale: Fig. 7

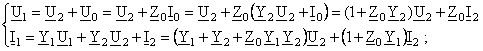
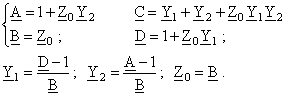(11)

Cuadripolul diport e simetric daca , deci .

2 Conexiuni ale cuadripolilor

2.1 Conexiunea in lant (cascada)

La aceasta conexiune (fig. 8), poarta de iesire a primului cuadripol e poarta de intrare pentru urmatorul. Este conexiunea larg raspandita. De la dipolul activ DA pana la dipolul pasiv DP, in figura 2 pot fi intercalati mai multi cuadripoli in lant: linia de transport CD₁, transformatorul CD₂, redresorul CD₃, filtrul CD₄, etc.

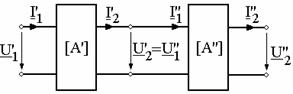
Fig. 8

Ansamblul celor doi cuadripoli in lant se comporta ca un singur cuadripol descris prin matricea [A] a parametrilor fundamentali definita prin relatia (3):

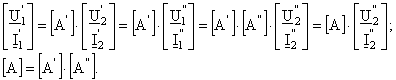(12)

2.2 Alte conexiuni

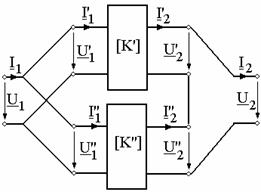a) Conexiunea paralel-serie din figura 9 prezinta portile de intrare conectate in paralel, iar portile de iesire in serie.

Se stabilesc relatiile:

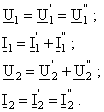(13) Fig. 9

E util a se defini matricea hibrida paralel-serie [K] astfel:

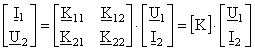. (14)

Matricea [K] se afla din matricea [A], prin explicitarea marimilor si din sistemul (1) si rezulta:

Conditia de reciprocitate intre parametrii hibrizi paralel-serie este:

,

iar conditia de simetrie devine:

Conexiunea paralel-serie a diportilor din figura 9 echivaleaza cu un cuadripol care are matricea hibrida [K]. Se utilizeaza relatiile (13):

Cuadripolul echivalent are deci matricea hibrida paralel-serie:

. (15)

Se procedeaza analog pentru urmatoarele trei conexiuni, demonstratiile fiind lasate pentru exercitiul cititorului.

b) Conexiunea paralel-paralel face apel la matricea admitanta [Y]:

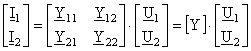, (16)

cu relatia de reciprocitate , iar conditia de simetrie .

Cuadripolul echivalent are matricea:

. (17)

c) Conexiunea serie-serie dintre doi cuadripoli necesita definirea matricei impedanta [Z]:

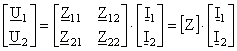, (18)

cu conditia de reciprocitate si simetrie daca .

Matricea impedanta a cuadripolului echivalent este:

. (19)

d) Conexiunea serie-paralel utilizeaza matricea hibrida serie-paralel [H], definita astfel:

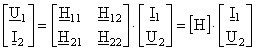. (20)

Intre cei patru parametri hibrizi exista relatia de reciprocitate , iar conditia de simetrie a cuadripolului este

Doi cuadripoli conectati serie-paralel echivaleaza cu unul singur caracterizat de matricea:

. (21)

3 Impedanta caracteristica

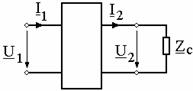Impedanta caracteristica a unui cuadripol, sau a unui lant de cuadripoli echivalent cu un singur cuadripol, este impedanta de sarcina care, conecteaza la poarta de iesire, se masoara nemodificata la poarta de intrare (fig. 10).

Astfel, in figura 2, daca receptorul DP are impedanta adaptata generatorului DA in vederea transferului maxim de putere activa, se poate intercala un cuadripol CD care are impedanta caracteristica a DP, fara ca intercalarea sa schimbe conditiile de adaptare.    Fig. 10

Impedanta caracteristica este deci:

. (22)

Sistemul (1) permite explicitarea impedantei :

;

,

iar e solutia acestei ecuatii.

In cazul cuadripolului simetric, (6):

, (23)

acceptandu-se pentru doar solutii care au partea reala (rezistenta) pozitiva, deci impedante realizabile cu componente pasive.

Observatie. Impedanta caracteristica depinde de frecventa (prin dependenta de frecventa a reactantelor cuadripolilor din lant), deci premizele, de neafectare a conditiilor de adaptare si transfer maxim de putere, sunt valabile doar pentru frecventa respectiva.

4 Constanta de propagare

In cazul unui lant de cuadripoli simetric, avand la iesire impedanta caracteristica, raportul intrare-iesire este acelasi, atat pentru tensiuni cat si pentru curenti, conform relatiei (22). Cuprinderea unui domeniu larg pentru acest raport se realizeaza definind constanta de propagare pe o scara logaritmica, astfel:

, (24)

sau in continuare :

;

.

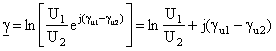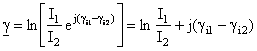Constanta de faza (de defazaj) e partea imaginara a constantei de propagare:

, [rad], (25)

defazajul fiind la iesire egal cu cel de la poarta de intrare:

. (26)

Constanta de atenuare e partea reala a constantei de propagare:

, [Np], (27)

insa, practic, daca se pune in discutie atenuarea unui semnal, intervine raportul puterilor intre intrare si iesire. Relatiile (26) si (27) dau:

,

astfel ca pentru constanta de atenuare rezulta:

, [Np]. (28)

Uneori se prefera pentru definirea constantei de atenuare o scara logaritmica zecimala:

[dB]. (29)

Intre unitatile de masura neper [Np] si decibell [dB] exista corespondentele:

1Np = 8,686 dB ; 1dB = 0,1151 Np.

Daca , atunci si intervine o atenuare pe lantul de cuadripoli. Daca , deci , are loc o amplificare (castig) a semnalului.

5 Filtre de frecventa

1 Caracterizare

Filtrele de frecventa sunt cuadripoli diporti intercalati intre generator si receptor (fig. 2), care se comporta selectiv fata de semnale de frecevente diferite. Lasa sa treaca neatenuate semnale cu frecventa cuprinsa in banda (intervalul) de trecere si atenueaza cat mai puternic semnalele cu frecventa in banda de oprire.

Aplicatiile sunt numeroase in comunicatii, instalatii de redresare, "netezirea" unor curenti nesinusoidali, etc. Constructiv, filtrele de frecventa sunt active sau pasive. Filtrele active pot realiza si amplificarea semnalului din banda de trecere.

In cele ce urmeaza ne vom ocupa de utilizarea ca filtre a unor cuadripoli reciproci, simetrici si adaptati (debitand pe impedanta caracteristica). Cum impedanta caracteristica depinde de frecventa, conditia adaptarii nu poate fi indeplinita pe toata gama de frecvente, ci doar pe o frecventa centrala din banda analizata.

Relatiile (1), completate cu (22) si (23), dau:

,

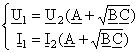astfel ca definitia (24) devine:

.

Datorita relatiei de reciprocitate (4) aplicate diportului simetric, la care (6):

.

Parametrul fundamental A are expresia:

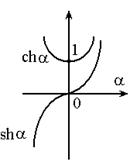
. (30)

Se amintesc, succint, cateva relatii matematice:

;

.

Fig. 11

Relatia (30), corelata cu (24), conduc la:

(31)

Filtrul nedisipativ este realizat cu bobine si condensatoare ideale, deci fara rezistoare. La schema T (10), respectiv schema echivalenta (11), parametrul fundamental este:

,

unde, la filtrul nedisipativ, admitantele complexe , si impedantele complexe , sunt pur imaginare. Aceasta face ca , respectiv relatia (31) conduce la concluzia:

; . (32)

a) Banda de trecere are , ,, deci:

. (33)

b) Banda de oprire, cu , are conform relatiei(32) , deci:

. (34)

Delimitarea intervalelor de trecere, respectiv oprire, are loc la frecvente de taiere, solutii ale ecuatiei:

. (35)

2 Filtre simetrice nedisipative

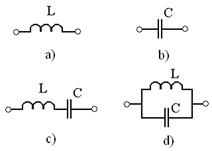
Utilizarea bobinelor si condensatoarelor la filtre se bazeaza pe variatia reactantei acestora cu frecventa (deci cu pulsatia). Bobina din figura 12a are impedanta care creste cu frecventa , iar condensatorul din figura 12b are impedanta care scade cu frecventa . Fig. 12

a) Filtrul trece jos (FTJ) opreste semnalele cu frecvente inalte. Filtrele T, respectiv , din figura 13, realizeaza cu bobine blocarea, iar cu condensatoare ocolirea portii de iesire de catre semnalele cu frecvente inalte.

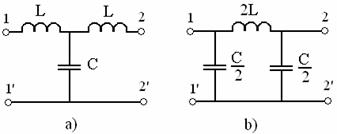
Fig. 13

Relatiile(10) si (11) dau, pentru schemele T si din figura 13, parametrii fundamentali A si D identici, dar B si C diferiti. Comportarea schemelor T si e similara numai la pulsatia .

b) Filtrul trece sus (FTS) din figura 14 realizeaza, invers, blocarea semnalelor de frecvente joase prin condensatoare, iar ocolirea cu bobine.

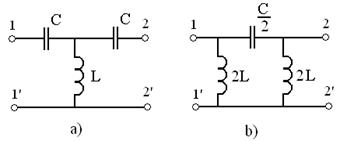
Fig. 14

Grupajul L-C serie din figura 12c are impedanta , nula la pulsatia de rezonanta . Grupajul L-C paralel din figura 12d, cu admitanta are la rezonanta Y=0 , .

c) Filtrul opreste banda (FOB) (fig. 15) apeleaza la modulul paralel pentru blocarea semnalelor dintr-o banda care are ca frecventa centrala frecventa de rezonanta si modulul in serie pentru traseul de ocolire al frecventelor nedorite.

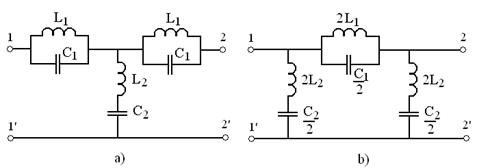
Fig. 15

d) Filtrul trece banda (FTB) din figura 16 utilizeaza aceleasi module, dar cu scop contrar: blocarea/ocolirea semnalelor cu frecvente mai joase sau mai inalte decat banda de trecere.

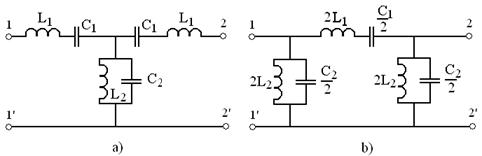
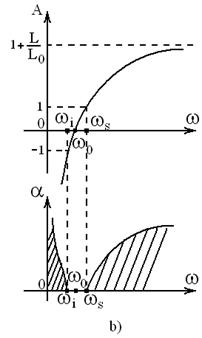Fig. 16

Se subliniaza din nou ca schemele T si nu sunt echivalente, caci nu toti parametrii fundamentali sunt identici, la orice frecventa.

3 Exemplu

Se cere calculul intervalului de trecere pentru filtrul de frecventa din figura 17a.

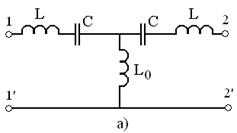
Fig. 17

Relatiile 10 dau:

Conditia (33) pentru banda de trecere: da limitele acestui interval (pulsatiile de taiere):

,

unde :

.

In reprezentarile grafice din figura 17b, A=0 la pulsatia:

.

Diportul functioneaza ca filtru trece banda. Constanta de atenuare (pentru intervalele de oprire) e data de (34).

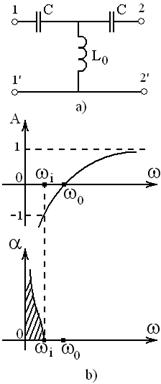
Cazul particular L=0, cu schema din figura 18a, da pulsatia superioara de taiere , deci filtrul este de tip trece sus.

Pulsatia devine:

,

iar pulsatia de taiere are valoarea:

.

Reprezentarile din figura 18b pun in evidenta variatiile A() si , constanta de atenuare fiind nenula pe intervalul , care e banda de oprire. Fig. 18