Scrigroup - Documente si articole

     

 
HomeDocumenteUploadResurseAlte limbi doc
 
AeronauticaComunicatiiElectronica electricitateMerceologieTehnica mecanica


Sisteme liniare I/O - Modelarea sistemelor liniare invariante in timp (LTI)

Electronica electricitate



+ Font mai mare | - Font mai mic



Sisteme liniare I/O

1 Modelarea sistemelor liniare invariante in timp (LTI).

i(t)



+

v(t) C v(t)


i(t) v(t)

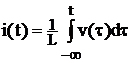
v(t) L v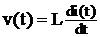(t)

i(t)

v(t) = R v(t)

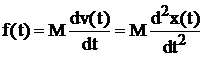
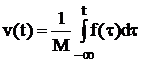(M ~C !)

k- constanta elastica

f

forta de compresie

forta de extensie

element de amortizare

f


Se observa analogii intre: M- C

k- L

D - R

;

;

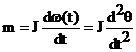
Combinatia unor astfel de elemente pot sa modeleze sisteme complexe.

Avand in vedere aceste modele de baza rezulta doua tipuri fundamentale de model.

Model ordin I :

sau

Daca consideram conditiile initiale nule si aplicam transformata Laplace ,atunci rezulta:

definim functie de transfer

Model ordin II .

sau

In cazul conditiilor initiale nule si aplicand transformata Laplace se determina functia de transfer

a sistemului de ordin II .

2. Sisteme LTI

Fie sistemul :

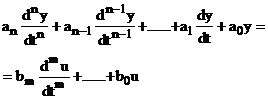
Considerand conditiile initiale nule

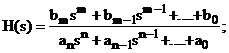
sau o forma normalizata

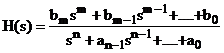
H(s)

 


u y

Avand functia de transfer H(s) vom defini urmatoarele marimi:

- fie ecuatia

Radacinile acestei ecuatii se numesc ZEROURI ai sistemului.

- fie ecuatia

Radacinile acestei ecuatii se numesc POLII sistemului.

Obs: - Orice ecuatie diferentiala neomogena are solutia formata din

solutia generala+solutia particulara

- Ecuatia care furnizeaza polii se mai numete ECUATIE CARACTERISTICA a sistemului

si va furniza solutia generala a ecuatiei diferentiale care modeleaza sistemul .

-Fie

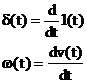
Raspunsul sistemului la semnal Dirac() se numete FUNCTIA PONDERE.

Raspunsul sistemului la treapta (1(t)) se numete FUNCTIE INDICIALA.

3 Algebra functiilor de transfer

1. Conexiune in serie

 

 

  n y

sunt functii de transfer.

Dorim sa calculam .

Avem

dar i .

Rezulta :

Generalizare:

fie ; i=1..n un numar finit de functii de transfer


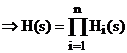
2. Conexiune in paralel

 

 

 
u    u u

u

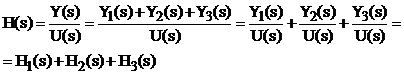
Generalizare :

fie i=1..n , functii de transfer in numar finit

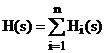
3.Conexiune cu reactie
 

 

u y

r

Avem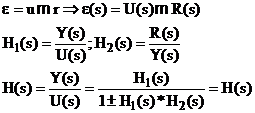


Obs: - pentru reactte pozitiva la numitor avem polinomul

- pentru reactie negativa la numitor avem polinomul

;

Functia de transfer a sistemului deschis

Fie sistemul

 

 

 
u y

Prin definitie , functia de transfer al sistemului deschis este:

deci

Obs

Fie sistemul : ramura directa
 

 
u    y


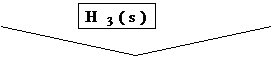
ramura de reactie
 

 

 

 
transformam u y

 

din care rezulta :

u y
 

 

 

 

5. Functia de transfer a elementului de comparatie

fie sistemul:
 
u y

r


Prin definitie:

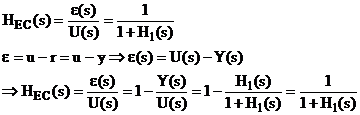
6. Functia de transfer a sistemelor cu zgomot.
 

 

 

 

z

u + y

r

- functia de transfer sistem

- functia de transfer regulator

- functia de transfer zgomot

- functia de transfer ramura de reactie

u - semnal de referinta

y - semnal de ieire

z - zgomot

Definim functia de transfer al sistemului inchis

functia de transfer al elementului de comparatie (eroare)

functia de transfer zgomot sistem

functia de transfer eroare zgomot

Astfel avem relatiile


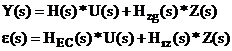
Se poate vedea


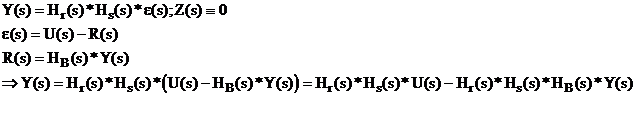
Marimea se numete amplificare bucla.

La fel :


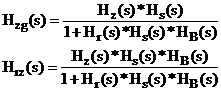
Politica de confidentialitate | Termeni si conditii de utilizare



DISTRIBUIE DOCUMENTUL

Comentarii


Vizualizari: 1632
Importanta: rank

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved