Criterii de stabilitate

Criterii de stabilitate

Datorita faptului ca aplicarea teoremei fundamentale a stabilitatii si a celorlalte metode de analiza a stabilitatii este uneori greu de aplicat s-au dezvoltat criterii algebrice si frecventiale prin intermediul carora se poate studia intr-un mod mai simplu stabilitatea sistemelor liniare.

A.Criterii algebrice de analiza a stabilitatii sistemelor liniare

Criteriile algebrice de analiza a stabilitatii sunt de fapt corolarii ale teoremei fundamentale a stabilitatii cu ajutorul carora se poate analiza stabilitatea unui sistem fara a fi nevoiti sa calculam in mod explicit radacinile polinomului caracteristic al sistemului, lucru care uneori poate deveni dificil (d.p.d.v. analitic).

Criteriile de stabilitate algebrice difera in cazul sistemelor liniare continue, fata de sistemele liniare discrete, existind criterii specifice pentru fiecare in parte.

Ø      Criterii de stabilitate algebrice pentru STC

Cele mai utilizate criterii de stabilitate algebrice pentru STC sunt criteriile Hurwitz si Routh. Aceste doua criterii sunt de fapt echivalente, difera doar modul de "prezentare".

1. Criteriul Hurwitz

Fie expresia:

, cu a_n>0    (3.19)

polinomul caracteristic al unui sistem liniar continuu.

Se defineste determinantul de ordinul n:

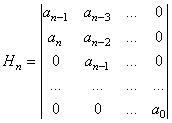(3.20)

care poarta numele de determinant Hurwitz. Fie:

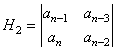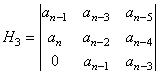, , s.a.m.d.

minorii de "N-V" ai determinantului Hurwitz. Criteriul de stabilitate Hurwitz se enunta astfel:

Sistemul de polinom caracteristic (3.19) este asimptotic stabil daca si numai daca este indeplinita conditia:

(3.21)

O conditie necesara, dar nu si suficienta pentru ca un STC sa fie stabil este ca toti coeficientii polinomului caracteristic sa aiba acelasi semn. Din acest motiv, daca aceasta conditie nu este indeplinita, nu se mai aplica nici unul dintre criteriile sau metodele de analiza a STC, fiind evident ca sistemul este instabil.

Daca toti coeficientii acestuia sunt negativi, forma (3.19) se inmulteste cu -1 si criteriul Hurwitz este aplicat rezultatului astfel obtinut.

Criteriul Hurwitz se utilizeaza de regula pentru analiza stabilitatii sistemelor de ordin redus si pentru determinarea domeniului de stabilitate functie de unul sau mai multi parametri. Acest criteriu nu poate fi aplicat la analiza stabilitatii STC cu timp mort.

Criteriul Routh

Pentru a analiza stabilitatea unui sistem cu ajutorul criteriului Routh se porneste de la polinomul caracteristic de forma (3.19) al sistemului. Cu ajutorul coeficientilor polinomului caracteristic se construieste un tabel cu (n+1) linii si coloane, numit schema lui Routh. Tabelul se construieste astfel:

pe prima si a doua linie se trec coeficientii polinomului caracteristic, alternativ, in ordinea descrescatoare a puterilor lui s; prima linie incepe cu a_n, iar a doua cu a_n-1;

pe prima coloana se trec, incepand cu linia a doua, coeficientii care au expresiile:

, i = 2,.,n (3.22)

liniile urmatoare se completeaza cu coeficientii obtinuti conform relatiei:

(3.23)

coloana a doua este coloana coeficientilor Routh.

Pentru o mai buna intelegere a modului in care se construieste schema lui Routh, aceasta se ilustreaza in tabelul 3.1.

Tabelul 3.1

Semnificatia notatiei x din tabelul 1 este urmatoarea:

daca n este par, numarul coeficientilor va fi impar, si pe linia a doua, dupa ultimul coeficient se va completa cu zero;

daca n este impar, numarul coeficientilor va fi par, iar ultimul element din linia a doua va fi a₀.

Criteriul lui Routh are urmatorul enunt:

Un sistem liniar continuu este asimptotic stabil daca si numai daca totii coeficientii Routh sunt strict pozitivi.

Criteriul lui Routh se preteaza pentru analiza sistemelor de ordin oricat de mare, fiind in acelasi timp usor de implementat numeric. Nici acest criteriu nu poate fi utilizat la analiza stabilitatii sistemelor cu timp mort.

Ø      Criterii de stabilitate algebrice pentru STD

Un criteriu de stabilitate algebric specific sistemelor liniare in timp discret este criteriul lui Jury. Punctul de plecare in analiza stabilitatii STD cu ajutorul acestui criteriu este expresia:

, cu a_n>0 (3.24)

considerata ca fiind polinomul caracteristic al STD.

Cu ajutorul coeficientilor polinomului (3.24) se construieste un tabel numit schema lui Jury. Acest tabel se construieste astfel:

prima pereche de linii se completeaza cu coeficientii polinomului caracteristic (3.24), in prima linie acestia fiind trecuti in ordine crescatoare a puterilor lui z, iar in cea de-a doua linie in ordine inversa;

prima linie din a doua pereche de linii se completeaza cu coeficienti care se calculeaza dua expresia (3.25), iar a doua linie cu coeficientii calculati anterior, dar in ordine inversa; restul perechilor de linii se vor completa in acest mod, pana la a (n-1)-a pereche de linii;

, k = 1,.,n-1 (3.25)

pe prima coloana a tabelului apar coeficientii lui Jury, cate unul pentru fiecare pereche de linii. Coeficientii lui Jury se calculeaza dupa urmatoarea formula:

(3.26)

Pentru o mai buna intelegere, se ilustreaza prin tabelul 3.2 modalitea de constructie a tabelului lui Jury.

Tabelul 3.2

Criteriul lui Jury se enunta astfel:

Un sistem liniar discret este asimptotic stabil daca si numai daca sunt indeplinite urmatoarele conditii:

, (3.27)

, (3.28)

(3.29)

La fel ca si criteriile algebrice pentru STC, criteriul Jury nu se poate aplica la sisteme cu timp mort. Acest criteriu se preteaza la studiul stabilitatii sistemelor discrete de ordin oricat de mare si la implementarea numerica.

Observatie: In cazul STD, analiza stabilitatii acestora se poate face si in functie de pasul de discretizare h, ca parametru.

B.Criterii frecventiale de analiza a stabilitatii sistemelor liniare

Criteriile frecventiale de analiza a stabilitatii sistemelor liniare se bazeaza pe studiul sistemelor in domeniul frecventa (pulsatie).

Prezentarea de fata se reduce doar la diferite forme ale criteriului frecvential de stabilitate al lui Nyquist, atat pentru STC, cat si pentru STD.

Ø      Criteriul lui Nyquist pentru STC

Criteriul lui Nyquist se aplica pornind de la structura din figura III.1:

Figura III.1

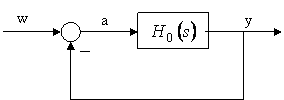
Exista doua variante ale criteriului, in functie de caracteristicile de care face uz pentru analiza stabilitatii, si anume: carecteristicile Bode, respectiv hodograful Nyquist.

In cazul in care se utilizeaza caracteristicile Bode, se defineste notiunea de rezerva de faza:

, (3.30)

unde w_t reprezinta pulsatia de taiere a sistemului.

Enuntul criteriului lui Nyquist care se bazeaza pe caracteristicile Bode este urmatorul:

Daca pentru sistemul cu reactie unitara din figura III.1 unde functia de transfer a sistemului deschis H₀(s) este de forma:

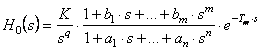(3.31)

unde K>0, qIsi T_m>0, cu polinoamele si prime intre ele, sistemul inchis este asimptotic stabil daca si numai daca se indeplineste conditia:

(3.32)

Ø      Criteriul lui Nyquist pentru STD

Fie sistemul cu reactie unitara din figura III.1, unde variabila s specifica STC se inlocuieste cu variabila z specifica STD. Criteriul de stabilitate Nyquist pentru STD bazat pe carecteristicile Bode se enunta astfel: Un sistem cu structura din figura VII.1 este asimptotic stabil daca este indeplinita conditia:

, (3.33)

unde n este ordinul sistemului, iar este numarul de poli ai sistemului deschis situati in interiorul cercului de raza unitate sau pe conturul acestuia.

Transformarea biliniara

Analiza stabilitatii STD poate fi realizata si cu ajutorul criteriilor specifice STC, utilizand transformarea biliniara data de expresia:

(3.34)

sau transformarea biliniara modificata:

(3.35)

Formulele de transformare inversa sunt urmatoarele:

(3.36)

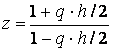(3.37)

In polinomul caracteristic al STD se inlocuieste variabila complexa z cu relatiile (3.36), (3.37) de variabila r sau q si asupra polinomului astfel obtinut se aplica apoi criteriile de stabilitate valabile in cazul STC.

Accesibilitatea si controlabilitatea sistemelor

Studiul accesibilitatii, controlabilitatii, cat si a observabilitatii nu difera de la STC la STD. Vom considera un sistem in spatiul starilor dat de relatiile (3.38), in variabila unificata:

(3.38)

Prin definitie, starea x₀ a unui sistem este controlabila daca exista o comanda care sa conduca sistemul, in timp finit, din starea x₀ in starea de repaos.

Pentru studiul controlabilitatii sistemelor liniare s-au dezvoltat unele criterii pornind de la MM-ISI al sistemului, cum sunt criteriile Kalman, respectiv Hausus.

A.Criteriul Kalman de analiza a controlabilitatii sistemelor liniare

Pornind de la sistemul (3.38), criteriul Kalman se enunta astfel (atat pentru STC, cat si pentru STD): Sistemul liniar (3.38) este controlabil daca si numai daca, matricea:

(3.39)

numita matrice de controlabilitate are rangul:

rang(M_c) = n , (3.40)

unde prin n s-a notat ordinul sistemului (3.38)

B.Criteriul Hausus de apreciere a controlabilitatii sistemelor liniare

Pornind de la sistemul dat de relatiile (3.38), criteriul Hausus se enunta astfel: Sistemul (3.38) este controlabil daca si numai daca, pentru orice lIs(A) este indeplinita conditia:

rang , (3.41)

unde prin n s-a notat ordinul sistemului (3.38).

Observabilitatea sistemelor

Prin definitie, o stare x₀ a unui sistem este neobservabila daca pe baza functiilor u(t) si y(t) cu tI t₀, t_f nu putem sa determinam starea sistemului la momentul t₀, x(t₀) = x₀.

Un sistem este observabil daca toate starile, in afara de starea de repaos x₀ = 0, sunt observabile.

Pentru analiza observabilitatii sistemelor se poate utiliza de asemenea criteriul Kalman.

A.Criteriul Kalman de analiza a observabilitatii sistemelor

Pornind de la sistemul dat de relatiile (3.38), criteriul Kalman de apreciere a observabilitatii sistemelor se enunta astfel: Sistemul dat de (3.38) este observabil daca si numai daca matricea:

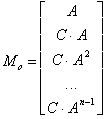(3.42)

numita si matrice de observabilitate, are rangul:

rang(M_o) = n , (3.43)

unde prin n s-a notat ordinul sistemului (3.38).

Pentru aprecierea globala atat a controlabilitatii, cat si a observabilitatii sistemelor, se poate utiliza criteriul lui Gilbert, care se enunta astfel: Fie functia de transfer a unui sistem S, de ordinul n, adusa la o forma ireductibila. Sistemul S este controlabil si observabil daca si numai daca:

grad(N₂) = n (3.44)

Observatie: Daca conditia (3.44) nu este indeplinita, nu putem sti care dintre proprietati este incalcata. Astfel, suntem obligati sa recurgem la criteriul Kalman pentru a determina care dintre proprietati (controlabilitatea sau observabilitatea), sau poate ambele, lipseste sistemului in cauza.

Cu toate ca atat pentru sistemele in timp continuu, cat si cele in timp discret se trateaza la fel problema controlabilitatii si observabilitatii, o chestiune importanta este alegerea perioadei de esantionare h, astfel incat controlabilitatea si observabilitatea sa nu se piarda prin discretizare. Astfel, daca un STC este controlabil (observabil), conditia ca proprietatea sa se pastreze si in urma discretizarii este:

(3.45)

pentru orice poli distincti p_a si p_b ai STC.