TOLERANTELE SI CONTROLUL ROTILOR DINTATE SI AL ANGRENAJELOR

TOLERANTELE SI CONTROLUL ROTILOR DINTATE SI AL ANGRENAJELOR

10.1. Elementele geometrice principale ale angrenajelor

cilindrice paralele

Angrenajele sunt mecanisme cu roti dintate care transmit miscarea de rotatie intre doi arbori sau transforma miscarea de rotatie in miscare de translatie si invers. Angrenajele sunt utilizate la un spectru larg de sisteme tehnice.

Dupa pozitia axelor in spatiu, angrenajele se clasifica in:

angrenaje cu axe paralele, formate din roti dintate cilindrice exterioare sau interioare (fig. 10.1.a);

angrenaje cu axe concurente, formate din roti dintate conice (fig. 10.1.b);

angrenaje cu axe incrucisate, formate din roti dintate elicoidale (fig. 10.1.c), roti dintate melcate (fig. 10.1.d), angrenaj hipoid (fig. 10.1.e).

Daca una din rotile dintate ale transmisiei are raza infinita (este o cremaliera), atunci rezulta un angrenaj cilindric cu cremaliera (fig. 10.1.f).

Intr-o sectiune perpendiculara pe cele doua axe ale angrenajului cilindric paralel se obtin cele doua cercuri de rostogolire si profilele dintilor la periferia lor. Cel mai utilizat tip de profil al flancurilor dintilor este profilul evolventic, datorita avantajelor pe care le prezinta (prelucrarea se face cu o scula simpla, cu profil rectiliniu, insensibilitate la variatia distantei dintre axe, s.a.). Profilul evolventic al flancului dintelui reprezinta o portiune dintr-o evolventa. Evolventa este curba descrisa de un punct oarecare de pe o dreapta MN care se roteste fara alunecare pe un cerc numit cerc de baza (fig. 10.2).

Ecuatiile parametrice ale evolventei

Miscarea de rostogolire fara alunecare a dreptei MN pe cercul de raza R_b determina egalitatea:

(10.1)

Tot din triunghiul MON rezulta:

(10.2)

Functia inv a (involuta de alfa) sau ev a (evolventa de alfa) este si tabelata.

Unghiul a format de raza corespunzatoare punctului M de pe evolventa si tangenta la evolventa in punctul considerat se numeste unghi de presiune. Daca punctul considerat M coincide cu polul angrenarii P, unghiul a se va numi unghi de angrenare (fig. 10.3).

Elementele geometrice ale angrenajelor sunt cuprinse in STAS 915/1,2,3-81. Dintre acestea, cele mai importante (fig. 10.3) sunt:

pasul danturii p masurat pe cercul de divizare, reprezinta distanta dintre doua flancuri omologe consecutive;

modulul m, este definit ca fiind raportul dintre pasul de divizare si numarul p ();

inaltimea dintelui h, este semidiferenta intre diametrele exterior si interior al rotii si se compune din h_a si h_f () unde h_a este inaltimea capului dintelui, h_f inaltimea piciorului dintelui;

D_a este diametrul cercului de cap (exterior);

D_f este diametrul cercului de picior (interior);

D_w este diametrul cercului de rostogolire;

D_b este diametrul cercului de baza;

a este distanta dintre axe;

p_b este pasul pe cercul de baza (de angrenare).

Dimensiunile elementelor geometrice ale rotilor dintate cilindrice se definesc in conformitate cu cremaliera de referinta (STAS 821-82), cremaliera de referinta fiind o portiune a unei roti dintate cilindrice cu diametrul infinit, al carui profil serveste ca baza pentru sistemul de angrenaje cu roti dintate cilindrice cu dinti drepti sau inclinati, avand profilul in evolventa (fig. 10.4). Cremaliera generatoare este negativul cremalierei de referinta sau inversa acesteia, numita astfel deoarece aceasta este profilul sculei aschietoare utilizata la generarea danturii rotii dintate.

Linia de referinta este linia pe care grosimea dintilor este egala cu golul dintre dinti. Liniile paralele cu linia de referinta se numesc linii de divizare.

Rularea intre cremaliera generatoare si roata se face intre linia de divizare a cremalierei, paralela cu linia de referinta si cercul de divizare al rotii (pe acest cerc pasul danturii este identic cu pasul cremalierei). Distanta dintre linia de referinta si linia de divizare se numeste deplasare absoluta a profilului si are expresia in care x este deplasarea specifica sau coeficientul de deplasare (fig. 10.5, fig. 10.6). Daca e = 0 (fig. 10.5), roata dintata nu are deplasare de profil; caracteristica acestor roti dintate este faptul ca cercurile de rostogolire sunt identice cu cercurile de divizare; daca e > 0 (fig. 10.6), adica cremaliera generatoare se departeaza de centrul rotii, deplasarea de profil este pozitiva si daca e < 0, adica cremaliera generatoare se apropie de axa rotii, deplasarea de profil este negativa.

10.2. Notiuni de precizie si control

Termenul de precizie, in literatura de specialitate este definit astfel:

precizia este eroarea maxima, in plus sau in minus, admisa la efectuarea unui calcul, a unei masuratori sau la realizarea unui produs;

precizia este proprietatea unui produs de a avea valorile marimilor sale caracteristice cuprinse intr-un interval cat mai mic in jurul valorii date.

Prin controlul unui produs industrial, in general, se intelege cuantificarea abaterilor micro si macrogeometrice, dimensionale si a pozitiilor relative ale suprafetelor si compararea lor cu cele prescrise de proiectant.

Dupa cum se cunoaste, precizia unui produs este determinata de rolul functional si de conditiile de lucru ale acestuia, functie de acestea se precizeaza limitele admisibile ale elementelor geometrice. Limitele admisibile in care trebuie sa se incadreze complexul de indicatori masurabili sunt ordonate in clase de precizie, continute in standardele de calitate ale rotilor dintate si angrenajelor.

Trepte de precizie si ajustaje

Normele romane si straine (STAS 6273-81, STAS 6460-81, STAS 6461-81, STAS 7395-81, ISO 1328-75, DIN 3963, GOST 1643 etc.) prevad 12 trepte de toleranta (precizie) pentru roti dintate si angrenaje, notate, in ordine descrescatoare a preciziei, cu cifrele 1 12.

Independent de treapta de precizie a rotilor dintate, se stabilesc sase tipuri de ajustaje a rotilor dintate in angrenare, notate cu literele A, B, C, D, E, H si opt tipuri de tolerante T_jn pentru jocul dintre flancurile dintilor, notate cu x, y, z, a, b, c, d, h. Notatiile sunt in ordinea scaderii marimii jocului minim garantat dintre flancuri J_{n min} si a tolerantei acestuia T_jn (fig. 10.7). La angrenajele cilindrice se prevad si sase trepte de precizie pentru abaterea distantei dintre axe (I, II, III, IV, V, VI) in ordinea scaderii preciziei (fig. 10.8)

Corespondenta tipului ajustajului cu tipul tolerantei jocului dintre flancuri si treapta de precizie a abaterii distantei dintre axe este prezentata in tabelul 10.1.

Tabelul 10.1

Alegerea treptei de precizie

Treptele de precizie pentru roti dintate si rugozitatile flancurilor active ale danturii se aleg in functie de conditiile de functionare, de domeniul de utilizare si de viteza periferica, avand in vedere si procedeul tehnologic de executie finala.

Recomandari privind alegerea treptei de precizie si a rugozitatilor flancurilor sunt date in STAS 12192-84 (Tabelul 2, ANEXA 2).

10.3. Criterii de precizie

Avand in vedere cele trei domenii mari de utilizare ale angrenajelor, cele patru standarde de tolerante, pentru angrenaje cilindrice (STAS 6273-81), pentru angrenaje conice si hipoide (STAS 6460-81), pentru angrenaje melcate (STAS 6461-81) si pentru angrenaje cu cremaliera (STAS 7395-81) prevad trei criterii de precizie.

- Criteriul de precizie cinematica, indica variatia unghiului de rotatie al rotii in timpul parcurgerii unghiului de 2p, destinat angrenajelor din lanturile cinematice de divizare ale masinilor unelte, de masurare si la angrenaje planetare.

- Criteriul de functionare lina, permite observarea vibratiilor ce apar in angrenaj, cauzate de erorile periodice, recomandat angrenajelor care trebuie sa lucreze la viteze mari ( m/s) linistit, cu vibratii si zgomote reduse.

- Criteriul de contact dintre dinti, caracterizeaza capacitatea portanta a flancurilor si depinde de proportia participarii flancului la transmiterea puterii, aplicat angrenajelor cu portanta ridicata.

Pentru fiecare din aceste trei criterii s-au stabilit o serie de indici determinati prin erorile valorilor efective fata de cele teoretice. Erorile care fac parte din fiecare criteriu de precizie se numesc indici de precizie. Fiecare criteriu de precizie contine un indice de precizie de baza, ce da o imagine complexa asupra preciziei rotii si angrenajului pentru criteriul respectiv.

Exemplu de notare a preciziei unui angrenaj cilindric avand treapta a 8-a dupa criteriul de precizie cinematica, treapta a 7-a dupa criteriul de functionare lina, treapta a 6-a dupa criteriul de contact intre dinti, cu tipul ajustajului B, tipul tolerantei jocului dintre flancuri a si respectarea corespondentei dintre tipul ajustajului si treapta abaterii distantei dintre axe:

8-7-6-Ba STAS 6273-81

In cazurile in care pentru unul dintre criterii nu se prescrie treapta de precizie, atunci in locul numarului respectiv se inscrie litera N. Daca pentru toate criteriile se prescrie aceeasi treapta de precizie, aceasta se scrie o singura data.

10.3.1. Criteriul de precizie cinematica

Dintre indicii de precizie ai acestui criteriu amintim:

- Eroarea cinematica (F'_ir);

- Eroarea cumulata de pas (F_pr);

- Eroarea de rostogolire (F_cr);

- Bataia radiala (F_rr);

- Variatia cotei peste dinti (F_vwr);

- Eroarea distantei dintre axe (F"_ir).

Eroarea cinematica (F'_ir)

Reprezinta diferenta dintre unghiul de rotire real si cel nominal al rotii dintate conduse in limita unei rotatii complete, in cazul angrenarii pe un singur flanc cu o roata etalon asezata la distanta nominala dintre axe.

In figura 10.9 este reprezentata grafic variatia unghiului de rotire functie de unghiul j (unghiul parcurs de roata).

Controlul erorii cinematice se face cu aparatul din figura 10.10, care se compune din doi arbori cu axe paralele 1 si 2; pe arborele 1 sunt montate roata de verificat 5, cadranul gradat 3 si roata de frictiune 4, iar pe arborele 2 sunt montate acul indicator 7, roata etalon 8 (se poate roti liber pe arbore), pe care se afla fixat sectorul gradat 10.

La controlul rotii de verificat, aceasta se roteste mecanic sau manual, in timp ce roata etalon se franeaza usor, pentru a avea angrenare pe un flanc. Diferenta intre unghiul de rotire al rotii controlate si unghiul de rotire transmis rotii etalon se citeste pe sectorul gradat 10 in functie de pozitia acului 7.

Eroarea cumulata de pas (F_pr)

Prin eroare cumulata de pas se intelege diferenta maxima dintre valoarea efectiva a unui numar oarecare de pasi si valoarea teoretica a aceluiasi numar de pasi, pentru toata roata.

Masurarea se face pe un cerc ce trece prin mijlocul inaltimii dintelui, concentric cu centrul de rotatie al rotii.

Calculul erorii cumulate de pas se face determinand in primul rand abaterile partiale ale pasului (A_pi) stabilite fata de primul pas considerat in general ca origine, apoi se determina media aritmetica a abaterilor pasului tinand seama de semnul abaterilor. Se continua calculul cu diferentele dintre abaterile partiale (A_pi) si media aritmetica calculata anterior, obtinand abaterea partiala relativa a pasului.

Prin adunarea algebrica succesiva de la pas la pas a abaterilor relative, se obtin erorile cumulate de pas (F_pr), cu care se traseaza diagrama erorii cumulate a pasului (F_pr) (fig. 10.11).

Graficul erorii cumulate este o linie franta (sinusoidala), la care diferenta dintre ordonatele cu valori limita va fi eroarea cumulata maxima. Eroarea cumulata de pas poate fi masurata direct, prin compararea unghiuri-lor de rotatie, cu aparate de divizare sau cu aparate de tipul pasametrelor, care masoara pasul pe cercul de baza (fig. 10.12).

Eroarea de rostogolire (F_cr)

Supranumita si eroare de rulare, este parte componenta a erorii cinematice a rotii dintate, care se determina prin eliminarea bataii radiale (F_rr) din eroarea cinematica (F'_ir).

Grosimea dintelui

Desi nu face parte din indicii de control, grosimea dintelui este un parametru important, cunoasterea sa fiind necesara stabilirii jocului dintre flancuri si adausului de prelucrare in timpul danturarii.

Se precizeaza faptul ca se masoara coarda dintelui (S_R) si nu arcul dintelui pe cercul de raza R.

Privind modul de masurare a grosimii dintelui, aceasta se poate face direct sau indirect. In continuare se trateaza metoda directa, cea indirecta prezentandu-se la studiul jocului dintre flancuri.

Prin coarda dintelui pe cercul de divizare (S_d) se intelege segmentul de dreapta limitat de punctele de intersectie ale flancurilor cu cercul de divizare.

La dantura exterioara dreapta, expresiile coardei de divizare (S_d) si a inaltimii la coarda de divizare se deduc urmarind figura 10.13.

(10.3)

j este unghiul la centru care subintinde coarda dintelui pe cercul de divizare, exprimat prin relatia

(10.4)

m_t - modul frontal;

z - numarul de dinti ai rotii;

x - deplasarea specifica;

(10.5)

unde: f₀ - coeficientul de inaltime al capului dintelui.

Pentru danturile exterioare cu dinti inclinati, masurarea se face intr-o sectiune normala pe directia dintelui. Relatiile de calcul au aspectul

(10.6)

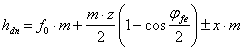(10.7)

unde: j_fe - unghiul la centru corespunzator grosimii dintelui pe cercul de divizare al rotii echivalente in plan frontal;

(10.8)

b_d - unghiul de inclinare a dintilor pe cercul de divizare;

(10.9)

Coarda constanta reprezinta distanta dintre punctele de tangenta ale profilului cremalierei de referinta cu flancurile dintelui. Expresiile corzii constante si a inaltimii la coarda constanta pentru dantura dreapta cilindrica (fig. 10.14) sunt:

sau

(10.10)

Inaltimea la coarda constanta (fig. 10.14)

, (10.11)

dar

(10.12)

(10.13)

Deoarece , rezulta:

(10.14)

unde este unghi de angrenare pe cercul de divizare.

Aparate pentru masurarea directa a grosimii dintilor

Aparatele utilizate la masurarea directa a corzii constante sau a corzii de divizare sunt sublerul pentru roti dintate, micrometrul optic si aparatul universal pentru masurat roti dintate. Sublerul pentru roti dintate (fig. 10.15.a) este o combinatie intre un subler obisnuit, cu care se masoara coarda S si un subler de adancime cu care se masoara inaltimea la coarda h. Precizia de masurare a acestuia este de 0,02 mm. Micrometrul optic (fig. 10.15.b) are, de asemenea, doua scari gradate, vizibile in ocularul 1, una verticala pentru masurarea inaltimii la coarda constanta si alta orizontala pentru masurarea grosimii dintelui, precizia de masurare fiind de 0,02 mm.

La masurarea corzii dintelui trebuie considerata influenta preciziei diametrului exterior al rotii, care in general este negativa.

Aparatul universal pentru masurat roti dintate K. Zeiss-Jena este prezentat in figura 10.27.

Bataia radiala (F_rr)

Bataia radiala reprezinta diferenta maxima a distantelor coardelor constante ale dintilor sau golurilor fata de axa de rotatie.

Masurarea bataii radiale se face conform schemei din figura 10.16.a. Roata dintata 1 este montata pe dornul 2 care materializeaza axa rotii de masurat 1. Diametrul palpatorului sferic 3 al aparatului 5 este astfel ales incat sa contacteze flancurile dintilor chiar in punctele extreme ale corzii constante a golului, materializand-o. Diferenta dintre valorile maxima si minima indicate de aparatul 5 la palparea tuturor golurilor, in acest caz, reprezinta bataia radiala a rotii. Indicatiile aparatului 5 pot fi inregistrate intr-o diagrama care va reprezenta variatia bataii radiale. Palpatorul 3 al aparatului poate avea si alte forme: prisma (fig. 10.16.b), materializand coarda constanta a dintelui sau trunchi de piramida (fig. 10.16.c).

In figura 10.17 sunt reprezen-tate schemele de principiu a doua aparate folosite la masurarea bataii radiale.

Bataia radiala a unei roti dintate se datoreaza atat excentricitatii coroanei dintate, cat si erorilor de divizare, avand deci o variatie sinusoidala, peste care se suprapune eroarea ciclica a fiecarui dinte. Preponderenta fiind excentricitatea, se poate accepta ca:

2 e F_rr

Lungimea peste dinti (W_N)

Lungimea (cota) peste dinti este distanta dintre doua plane paralele, tangente la flancurile opuse ale unui numar N de dinti cuprinsi intre cele doua plane.

Deoarece lungimea peste N dinti este segmentul care genereaza evolventele tangentate de suprafetele de masurare, marimea acestuia este egala cu lungimea arcului pe cercul de baza cuprins intre aceste flancuri.

W_N = (N - 1) p_b + S_b sau W_N = r_b [(N - 1) g_pb g_sb (10.15)

in care: g_pb - unghiul la centru corespunzator pasului de baza (p_b);

g_sb - unghiul la centru al grosimii dintelui pe cercul de baza;

a_t - unghiul de presiune frontal.

Din figura 10.18 rezulta:

g_sb g_sd inv a

Explicitand si inlocuind, rezulta:

(10.17)

Pentru danturile deplasate, relatia devine:

(10.18)

Numarul N peste care se masoara cota se stabileste, in cazul danturilor drepte nedeplasate, respectand conditia ca aceasta linie AB sa intersecteze cele doua flancuri chiar pe cercul de divizare, iar arcul care o subintinde, sa fie un multiplu intreg si fara sot al jumatatii de pas.

Numarul de semipasi va fi

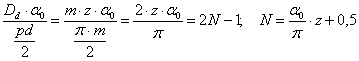(10.19)

pentru danturile drepte deplasate

(10.20)

Pentru rotile cu dinti inclinati se va considera numarul de dinti ai rotii echivalente sau de inlocuire:

(10.21)

admitand (10.22)

Valorile se rotunjesc la numarul intreg cel mai apropiat de dinti.

Lungimea peste dinti se masoara cu ajutorul sublerului, micrometrului cu talere pentru roti dintate, pasametrelor cu talere sau aparatului universal pentru roti dintate.

Variatia distantei dintre axe (F"_ir , f"_ir)

Aceasta reprezinta diferenta dintre valoarea maxima si minima a distantei masurate intre axe la angrenarea fara joc a rotii de masurat cu roata etalon in limitele unei rotatii complete a rotii care se verifica (F'_ir), respectiv la rotirea ei cu un dinte (f'_ir).

Masurarea variatiei distantei dintre axe este considerata un control complex al rotii in angrenare pe ambele flancuri cu o roata etalon.

Evaluarea se face cu aparatul prezentat principial in figura 10.19, care se compune din doi arbori 1 si 4; roata care se verifica 2 montata pe arborele 1 cu axa fixa si roata etalon 3 montata pe arborele 4 de pe culisa 6; arcul 7 asigura angrenarea fara joc intre cele doua roti. Variatia distantei dintre axe este indicata si inregistrata de aparatul 5. Aceasta eroare compusa cuprinde excentricitatea coroanei, erori ale flancurilor, ale directiei dintilor, ale formei, ale grosimii dintilor etc. Cu acest aparat, care datorita simplitatii are o larga raspandire, se inregistreaza simultan, fara a fi separate, aceste erori.

Variatia distantei dintre axe, care respecta legea cosinusoidala, este prezentata grafic in figura 10.20.

Indicii de precizie si complexele de indici de precizie pentru criteriul de precizie cinematica, in functie de treapta de precizie, sunt prezentati in tabelul 6, ANEXA 2.

10.3.2. Criteriul de functionare lina

Acest criteriu stabileste valoarea componentelor erorii totale a unghiului de rotire care se repeta de mai multe ori in timpul unei rotatii. Dintre indicii criteriului de functionare lina amintim:

- abaterea ciclica a angrenajului (f_zkr), respectiv toleranta abaterii ciclice (f_zk);

- eroarea formei profilului (f_fr);

- abaterea pasului pe cercul de baza (f_pb);

- toleranta variatiei distantei intre axe.

O parte din indicii acestui criteriu apartin si criteriului cinematic, unde au fost definiti si asupra carora nu se va reveni.

Abaterea ciclica, este componenta armonica a curbei abaterii cinematice a angrenajului. Mai exact, reprezinta valoarea medie a amplitudinilor oscilatiilor erorii cinematice in timpul rotirii cu 360 a rotii de verificat in angrenare pe un flanc cu roata etalon (fig. 10.9).

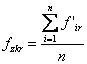(10.23)

Aparatura utilizata la masurarea abaterii ciclice este asemanatoare cu cea folosita la determinarea erorii cinematice, inregistrarea fiind absolut necesara.

Eroarea formei profilului (f_fr) sau eroarea profilului reprezinta (conform STAS 6273-81) distanta masurata pe normala intre doua profile teoretice in evolventa care tangenteaza profilul real (fig. 10.21).

Definitia se refera la profile evolventice deoarece, cu foarte mici exceptii, profilele dintilor rotilor dintate utilizate in constructia de masini si aparate sunt in arc de evolventa.

Eroarea de profil se poate masura cu ajutorul sabloanelor, proiectoarelor de profil, microscoapelor si evolventmetrelor.

Controlul formei profilului cu ajutorul sabloanelor se aplica rotilor dintate cu modul mare si se verifica profilul dintelui sau al golului dintre dinti prin metoda fantei de lumina (fig. 10.22).

Sabloanele sunt confectionate din tabla de otel si sunt folosite la controlul rotilor de precizie scazuta.

Proiectoarele de profil sunt utilizate la controlul rotilor dintate cu modul mic, prin marirea, de un numar de ori si masurarea pe ecran a abaterilor de forma ale dintelui real fata de profilul teoretic trasat pe hartie de calc la scara corespunzatoare.

Trasarea profilului evolventic marit se explica la masurarea abaterilor de forma cu ajutorul microscoapelor.

Masurarea erorii profilului cu ajutorul microscopului

Aceasta metoda se foloseste in cazul rotilor dintate cu dinti drepti si modul mic, cand folosirea aparatelor speciale nu este posibila. Metoda comporta trei etape:

I.           trasarea prin puncte a profilului evolventic teoretic, pe hartie de calc, la o scara egala cu factorul de amplificare al microscopului universal;

II.        trasarea prin puncte a profilului evolventic efectiv, coordonatele punctelor (x_i, y_i) fiind obtinute prin masuratori cu ajutorul microscopului de atelier (fig. 10.23);

III.      compararea prin suprapunere si evaluarea pe normala profilului teoretic a abaterilor de forma ale flancului dintelui (f_fr).

Masurarea erorii profilului cu ajutorul evolventmetrelor

Evolventmetrele sunt aparate specializate care indica abaterea profilului real al dintelui de la forma corecta a acestuia. Evolventmetrele pot fi cu discuri amovibile sau universale.

Evolventmetrele cu discuri amovibile sunt relativ simple, necesitand insa, pentru fiecare roata cu un alt diametru de baza, alt disc. Sunt cunoscute trei solutii constructive: cu rigla mobila (fig. 10.24.a), cu rigla fixa (fig. 10.24.b) si cu disc fix (fig. 10.24.c).

Schema evolventmetrului cu discuri amovibile din figura 10.24.a se compune din roata 1, care se verifica si se monteaza solidar cu discul 2, al carui diametru exterior este egal cu diametrul cercului de baza al rotii dintate 1. Sania 3 se deplaseaza rectiliniu cu o viteza egala cu viteza tangentiala a discului 2. Constructiv, identitatea dintre viteza de deplasare a saniei si viteza periferica a discului este asigurata de benzile metalice elastice care au un capat fixat de sanie, iar celalalt de disc. La deplasarea saniei 3, parghia 4, datorita arcului 5, urmareste profilul dintelui, transmitand comparatorului 6 abaterile evolventei efective fata de cea teoretica. Evolventa teoretica, conform definitiei, este creata de pozitia fixa a varfului palpatorului, parghiei 4, la deplasarea saniei.

Folosirea acestor aparate este justificata la productia de serie mare si masa.

Evolventmetrele universale folosesc un singur disc pentru controlul unei game dimensionale largi. Au o constructie complicata si costisitoare, motiv pentru care sunt utilizate in laboratoarele de masuratori.

Abaterea pasului pe cercul de baza (f_pbr)

Abaterea pasului pe cercul de baza sau a pasului de angrenare este un indice de precizie care exprima calitatea divizarii, caracterizand functionarea lina a angrenajului, de care depind vibratiile, zgomotul si uzura acestuia.

Abaterea pasului de baza (f_pbr) este diferenta dintre pasul de baza efectiv si pasul nominal, pentru fiecare dinte (fig. 10.25).

Valoarea nominala a pasului de baza se obtine cu relatia

p_b = p_d cos a

unde p_d este pasul masurat pe cercul de divizare. Eroarea pasului de baza determina, la randul sau, eroarea unghiului de angrenare Da_0n, care are expresia

(10.25)

semnul minus indicand o variatie inversa a celor doua abateri.

Masurarea pasului de baza se poate face cu pasametre portabile sau stationare sau cu aparatul universal pentru masurarea rotilor dintate. Principiul masurarii se bazeaza pe cele doua proprietati ale pasului de baza:

- este cea mai mica distanta dintre doua flancuri omonime;

- se afla pe linia de angrenare.

Pe baza acestui principiu s-au construit numeroase aparate, ale caror scheme cinematice sunt prezentate in figura 10.26.

Aparatul universal KARL ZEISS (fig. 10.27) consta dintr-un batiu 1 si un suport 2, care se roteste in plan orizontal. Pe suportul 2 se ghideaza un alt suport 4, pe care sunt fixate varfurile 5 intre care se aseaza roata de controlat, blocata de tija 6 prevazuta cu varf sferic care intra in golul danturii. Pe masuta 7 este montata instalatia de masurare 3, prevazuta cu diferite accesorii si doua comparatoare 8 si 9 (comparatorul 8 controleaza bataia radiala, iar comparatorul 9 erorile pasului, variatia lungimii peste dinti s.a.). Saniile 10 si 11 asigura deplasarea longitudinala si transversala ale ansamblului de masurat 3.

Precizia de masurare este 0,001 mm.

La controlul pasului de baza se va evita zona flancului de la capul sau piciorul dintelui.

Indirect, pasul de baza se poate obtine prin masurarea cotei peste dinti (N) si respectiv (N + 1).

(10.26)

Indicii de precizie si complexele de indici de precizie pentru criteriul de functionare lina, in functie de treapta de precizie sunt indicati in tabelul 7, ANEXA 2 si anume pentru treptele de precizie de la 3 la 8 si valorile limita ale gradului de acoperire suplimentar nominal e_b, iar pentru treptele de la 9 la 12, independent de e_b

Valorile limita pentru e_b sunt prezentate in tabelul 8, ANEXA 2, in functie de treapta de precizie a criteriului de contact dintre dinti.

10.3.3. Criteriul de contact

Dintre indicii acestui criteriu amintim:

pata de contact;

abaterea pasilor axiali;

abaterea directiei dintelui;

abaterea totala a liniei de contact;

abaterea de la paralelism a axelor.

Pata de contact, reprezinta suprafata efectiva a flancului dintelui controlat care vine in contact cu flancul dintelui conjugat. Determinarea petei de contact se face pe angrenajul real montat in pozitie de functionare, cu ajutorul informatorilor (vopselelor). Se acopera cu un strat subtire de vopsea (gros de 4 - 6 mm) flancurile rotii mici, se realizeaza angrenarea, rotind cu 360º roata mare usor franata. Cu ajutorul hartiei de filtru se copie pata de contact de pe dintii rotii mari si se masoara. Ca vopsele sunt utilizate: albastrul de Prusia, albul de zinc sau plumb, etc.

Dimensiunile petei de contact sunt evaluate procentual din dimensiunile flancului utilizabil (fig. 10.28):

- pe inaltimea dintelui: [%] (10.27)

- pe lungimea dintelui: [%] (10.28)

unde    h_med - inaltimea mijlocie a petei;

h_u - inaltimea utilizabila a flancului;

l₁ - distanta punctelor extreme ale petei;

l₂ - lungimea intreruperii petei;

l - lungimea dintelui.

Abaterea pasilor axiali (F_pxr) este diferenta dintre distantele efectiva si nominala dintre doua flancuri omologe ale dintilor, pe aceeasi generatoare de divizare (fig. 10.29). Abaterea pasilor axiali in plan normal se calculeaza cu relatia

(10.29)

in care b este unghiul de inclinare a dintelui.

Abaterea directiei dintelui (F_br reprezinta marimea arcului de cerc limitat de directiile efectiva si nominala ale dintelui (sau liniile de divizare ale acestuia) masurat pe un cerc ce trece aproximativ prin jumatatea inaltimii dintelui aflat intr-un plan frontal extrem al rotii (fig. 10.30).

(10.30)

fiind abaterea unghiului de inclinare a elicei dintelui pe cercul de divizare.

Masurarea unghiului de inclinare b se poate face fie direct, fie indirect.

La masurarea directa a unghiului de inclinare b pe cilindrul de divizare se folosesc aparate speciale (construite de firme ca DAVID BRAWN, MAAG, etc. si descrise in lucrarea [16]). Aceste aparate, asemanatoare principial, dar cu deosebiri constructive, obtin elicea teoretica din combinarea miscarii de rotatie cu miscarea rectilinie, pe care o compara cu elicea reala a dintelui.

Indirect, unghiul de inclinare a dintelui se obtine masurand pasul axial al dintelui, din relatia:

(10.31)

Metoda indirecta se recomanda rotilor dintate late.

Abaterea totala a liniei de contact (F_kr)

Distanta masurata pe normala dintre doua drepte paralele cu linia de contact nominala, situate in planul de angrenare (plan tangent la cilindrul de baza), care tangenteaza linia de contact efectiva (fig. 10.31).

Abaterea liniei de contact se poate masura fie cu aparate universale pentru masurat roti dintate, fie cu aparate speciale, numite contactometre. In figura 10.32 se prezinta schema de principiu a unui contactometru portabil. Prisma 1, cu forma dintelui cremalierei corespunzatoare, se aseaza in golul dintre doi dinti vecini. Pe cadrul 3, solidar cu prisma de reazem 1, se deplaseaza, in lungul dintelui, bratul mobil 4, pe care se gaseste palpatorul lama 2, care palpeaza flancul de controlat in lungul liniei de contact.

Abaterile liniei de contact reala fata de cea nominala sunt masurate de aparatul 6. Reazemul suplimentar 5 se bazeaza pe cilindrul exterior al rotii si serveste la pozitionarea corecta a contactometrului pe roata de controlat.

Abaterea de la paralelism a axelor are doua componente:

- abaterea de la paralelism sau neparalelismul axelor de rotatie ale rotilor pe planul lor teoretic comun (f_xr).

- neparalelismul proiectiilor axelor de rotatie ale rotilor pe un plan perpendicular pe planul teoretic comun (f_yr).

Ambele componente ale abaterii de la paralelism a axelor se determina in sectiune frontala, in unitati de lungime raportate la latimea de lucru B a danturii (fig. 10.33). Determinarea abaterilor de la paralelism se face aplicand principiul materializarii axelor, folosind chiar arborii rotilor dintate, montati in lagarele carcasei sau dornuri de control speciale. Pentru aceasta se pot folosi: platoul de control, nivela de inalta precizie, echer, cale, micrometre si comparatoare cu suporti. Metoda efectiva de determinare este prezentata la controlul abaterilor de pozitie in capitolul2.

Indicii de precizie si complexele de indici de precizie pentru criteriul de contact dintre dinti se aleg conform tabelului 9, ANEXA 2 si anume in functie de valorile limita ale gradului de acoperire suplimentar, nominal e_b din tabelul 8 (ANEXA 2) si treapta de precizie.

Jocul dintre flancuri

Pentru functionarea corecta a unui angrenaj, intre rotile dintate ale acestuia trebuie sa existe un joc. Acest joc se stabileste independent de clasa de precizie si este necesar pentru a compensa erorile de fabricatie si de montaj, dilatatiile termice, mentinerea peliculei lubrifiante, etc.

Jocul dintre flancuri (J_n) este jocul dintre flancurile neactive ale dintilor, in planul de angrenare (fig. 10.34).

Jocul dintre flancuri se poate realiza prin:

deplasarea suplimentara a profilului;

abaterea limita a distantei intre axe.

Deplasarea suplimentara a profilului de referinta (E_Hr) este deplasarea negativa a profilului de referinta (spre axa rotii) din pozitia nominala, prin care se micsoreaza grosimea dintelui si se creaza jocul intre flancuri (fig. 10.35). Pozitia nominala a profilului de referinta se considera o pozitie conventionala a profilului de referinta, fata de o roata dintata fara erori (etalon), pozitionata la distanta H dintre axa de lucru a rotii dintate si dreapta de divizare a profilului de referinta, calculata cu relatia

in care este deplasarea nominala a profilului de referinta.

Deplasarea suplimentara minima a profilului de referinta este:

pentru dantura exterioara E_Hs;

pentru dantura interioara E_Hi.

T_H este toleranta deplasarii suplimentare a profilului de referinta.

Intre jocul dintre flancuri si deplasarea profilului de referinta exista relatia:

Controlul deplasarii suplimentare a profilului se poate face direct sau indirect.

Controlul direct al deplasarii suplimentare a profilului de referinta se face cu ajutorul unui comparator prevazut cu palpator-furca. Cu acesta se verifica fiecare dinte al rotii dintate si se citesc abaterile. Initial, aparatul a fost reglat cu ajutorul unei roti etalon cu profil nedeplasat (x = 0). Controlul grosimii dintelui se face cu ajutorul sublerului pentru roti dintate sau cu ajutorul micrometrului optic.

Masurarea indirecta a deplasarii suplimentare se poate face prin masurarea cotei peste dinti (metoda prezentata la controlul lungimii peste dinti) sau prin masurarea cotei (dimensiunii) peste bile sau role, pentru danturi exterioare, si intre bile sau role, pentru danturi interioare.

Calculul cotei peste bile sau role. Conform figurii 10.36.a (pentru roti cu numar par de dinti)

unde: R_a - raza cercului centrelor bilelor sau rolelor;

- diametrul rolei sau bilei.

Daca se traseaza evolventa ce trece prin centrul bilei sau rolei (fig. 10.36.b), atunci

unde este unghiul de presiune (angrenare) corespunzator cercului pe care se afla centrele bilelor sau rolelor.

Conform figurii 10.36.b si c:

Cu valoarea calculata cu relatia (10.37), folosind tabelul functiei inv (ev a - Tabelul 1, ANEXA 2) se determina valoarea unghiului , cu care se calculeaza valoarea lui R_a si apoi M.

Pentru rotile cu numar impar de dinti (fig. 10.37), cota peste bile sau role se calculeaza cu relatia:

Calculul dimensiunii intre role sau bile la danturile interioare. Pentru dantura interioara cu numar par de dinti (fig. 10.38.a), expresia cotei intre role sau bile este:

(10.39)

sau (10.40)

Conform figurii 10.39:

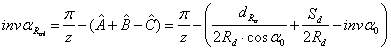
Pentru dantura interioara cu numar impar de dinti (fig. 10.38.b):

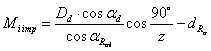
Abaterea a acestei cote se datoreaza abaterii grosimii dintelui care, in cazul danturii drepte, va fi si care determina jocul intre flancuri,

La danturile inclinate, in relatiile de mai sus se modifica corespunzator parametrii m_n, a_0n, x_n.

La danturile deplasate, grosimea dintelui pe cercul de divizare devine:

La controlul acestor dimensiuni se pot folosi aparate cu suprafete de masurare plane utilizand bile asezate pe cale plan-paralele la roti dintate cilindrice cu dinti inclinati (fig. 10.40) si role la roti dintate cilindrice cu dinti drepti.

10.4. Alegerea tipului de ajustaj

Independent de treapta de precizie adoptata pentru roti si rugozitatile flancurilor active ale dintilor, trebuie precizat si tipul ajustajului rotilor dintate aflate in angrenare.

Alegerea tipului de ajustaj al rotilor dintate in angrenare se face pe baza calcului jocului minim dintre flancuri, in functie de:

regimul termic al angrenajului;

viteza periferica a rotilor dintate;

si, in cazul angrenajelor cinematice la care este necesara limitarea unghiului de rotire libera a rotilor dintate, pe baza jocului maxim dintre flancuri.

Jocul minim necesar dintre flancuri, se calculeaza cu relatia

(10.45)

unde: - jocul minim necesar dintre flancuri, rezulta din conditia compensarii dilatarii termice inegale dintre carcasa si angrenaj;

- jocul minim necesar dintre flancuri, functie de viteza periferica a rotilor dintate care trebuie sa satisfaca conditia

(10.46)

unde - jocul minim dintre flancuri, calculat conform standardului prin care se reglementeaza sistemul de tolerante pentru tipul respectiv de angrenaj.

Jocul minim necesar dintre flancuri, functie de regimul termic al angrenajului se calculeaza cu urmatoarea relatie pentru angrenajele cilindrice

[mm]    (10.47)

unde: - distanta dintre axe, in milimetri;

- coeficientul de dilatare liniara pentru materialul rotilor dintate, respectiv al carcasei;

- diferenta de crestere a temperaturii, fata de 20⁰ C, a rotilor dintate, respectiv a carcasei;

- unghiul de angrenare normal al profilului de referinta.

Jocul minim necesar dintre flancuri functie de viteza periferica se calculeaza cu relatia

[mm] (10.48)

unde: - modulul normal al danturii, in milimetri.

Factorul 10 corespunde unor transmisii lente, iar 30 unor transmisii rapide. Pentru angrenaje cinematice lente, fara ungere fortata, se poate adopta: mm.

Jocul maxim dintre flancuri corespunzator unghiului maxim admis de rotire libera a rotilor dintate in angrenajele cinematice se calculeaza cu urmatoarele relatii pentru angrenajele cilindrice

[mm]    (10.49)

unde: - unghiul maxim admis de rotire libera a rotilor dintate in angrenaj, in secunde.

Valoarea care se adopta pentru angrenaj trebuie sa satisfaca conditia:

si se calculeaza cu relatia

[mm] (10.50)

in care: - jocul minim dintre flancuri, standardizat, in micrometri;

- toleranta standardizata a deplasarii suplimentare a profilului de referinta a pinionului, respectiv a rotii, in micrometri;

- abaterea limita standardizata a distantei intre axe, in micrometri;

- numarul de dinti ai rotii dintate.

Pentru angrenajele conice si melcate, alegerea tipului de ajustaj se face conform STAS 12192-84.

10.5. Exemple de calcul

Calculul parametrilor de control ai angrenajelor cilindrice exterioare (S_c; h_c; N; W_N; M) si verificarea conditiilor de masurare a acestora se efectueaza, de regula, la finalul calculului geometric al angrenajului.

In tabelul 10.2 se prezinta sistematizat acest calcul, considerand doua exemple numerice pentru angrenaje cu dinti drepti: primul pentru angrenaj la care nu se impune distanta dintre axe (), iar al doilea pentru un angrenaj la care se impune distanta dintre axe ( . Prezentarea detaliata a calculului geometric, a calculului de rezistenta si a calculului parametrilor de control pentru toate tipurile de angrenaje sunt redate in lucrarea [27].

Tabelul 10.2