Elemente privind prelucrarea datelor experimentale - cercetare stiintifica

Elemente privind prelucrarea datelor experimentale

Generalitati asupra modalitatii de intocmire a unei lucrari de cercetare stiintifica

Din punct de vedere structural o lucrare de cercetare stiintifica cu caracter experimental se recomanda sa fie organizata dupa urmatoarele paragrafe :

a) Introducere.

In preambulul lucrarii se obisnuieste sa se prezinte succint scopul lucrarii, cu mentionarea sintetica a rezultatelor obtinute in domeniul respectiv de catre alti cercetatori.

b) Instalatia experimentala si metodica de cercetare presupune prezentarea schemei de principiu a statiunii experimentale cu indicarea expresa a punctelor de masura. Se prezinta apoi succint conditiile ambiante in care s-au realizat masuratorile, regimurile functionale cercetate precum si metodologia si mijloacele care au servit la evaluarea parametrilor ce prezinta interes.

c) Prelucrarea datelor experimentale trebuie sa se bucure de o atentie deosebita din partea cercetatorului. Deoarece de regula procesele complexe care caracterizeaza functionarea masinilor termice se evalueaza prin procedee de masurare indirecta, trebuind avut in vedere felul cum se propaga erorile sistematice si intamplatoare asupra rezultatului masurarii ( vezi paragraful 2.4. ) .

Pentru cercetator este imperios necesar sa cunoasca modul in care se rotunjesc rezultatele precum si simplificarile de calcul pe care le poate utiliza. Data fiind importanta pastrarii cel putin temporare a rezultatelor experimentelor, este importanta de asemenea prezentarea lor sub o forma convenabila, intuitiva, in scopul utilizarii. Astfel toate datele, daca nu sunt disperate, sunt stranse si prelucrate sub forma unor tabele, grafice, nomograme sau ecuatii.

d) Interpretarea rezultatelor obtinute are in vedere discutarea lor critica, eventual in juxtapunere cu rezultatele obtinute de alti cercetatori.

e) Concluziile prezinta in sinteza principalele rezultate obtinute cu indicarea corelatiei intre parametrii variabila dependenta si independenta. Se recomanda tot odata inventarierea problemelor ce mai trebuiesc cercetate pentru o elucidare completa a fenomenelor luate in studiu.

f) Lucrarea se incheie cu lista de bibliografie ( titlurile fiind indicate in text cu cifre arabe si intre paranteze ) si cu rezumatul lucrarii, de obicei in doua limbi de circulatie mondiala.

2. Reguli de rotunjire a rezultatelor

Pentru un sir de masurari, erorile aflate arata si care cifre anume din valoarea numerica, considerata ca rezultat al masurarilor sunt indoielnice.

In adevar, nu are sens sa exprimam eroarea printr-un numar mare de cifre, fiind cel mai des indicat sa ne limitam la o singura cifra semnificativa.

Numai rareori se dau erorile cu doua cifre semnificative, cum este cazul masurarilor foarte precise precum si atunci cand numarul exprimat prin 2 cifre e mai mic decat 30.

De asemenea si rotunjirea valorii numerice a rezultatului masurarii trebuie sa se faca in concordanta cu eroarea rezultatului, adica valoarea rezultatului trebuie sa se termine cel mult cu o cifra de acelasi ordin cu valoarea erorii.

Dupa regulile calculului aproximatiilor rotunjirea se face astfel :

1. Cifrele de prisos la numere intregi se inlocuiesc cu zero iar la fractiile zecimale se elimina.

2. Daca prima cifra inlocuita cu zero sau eliminata este mai mica decat 5, atunci cifrele ramase nu se schimba.

Daca prima cifra inlocuita cu 0 sau eliminata este mai mare decat 5 sau egala cu 5 iar cifrele ce urmeaza nu sunt zero, atunci ultima cifra din numarul rotunjit se mareste cu o unitate.

4. Daca cifra 5 se inlocuieste cu 0 sau se elimina, singura sau cu zerourile care urmeaza, atunci ultima cifra din numarul rotunjit ramane neschimbata daca este cu sot si se mareste cu o unitate daca e fara sot. In acest caz, operatia poarta numele de rotunjire pana la un numar cu sot.

Daca valoarea numerica este exprimata printr-un numar zecimal, se mai poate pastra inca o cifra care este de orientare si se scrie mai jos.

3 Simplificari de calcule utilizate la evaluarea erorilor

Daca in calculul erorilor, se lucreaza cu "valori mici" , se recomanda, pentru expeditivitate, utilizarea urmatoarelor relatii simplificate :

( 1 )

Daca are valori foarte mici :

( 2 )

La functiile trigonometrice :

in radiani ( 3 )

La calcule de precizie mai ridicata se poate folosi :

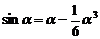
si in sfarsit :

( 4 )

4. Reprezentarea datelor prin tabele

Orice masurare implica dupa cum se stie cel putin doua variabile, una presupusa independenta si alta dependenta. In reprezentarea datelor prin tabele, variabilele dependente si independente admise, precum si relatiile dintre ele, daca exista, sunt exprimate prin insasi aranjarea corespunzatoare a valorilor sau a proprietatilor variabilelor, intr-o schema ordonata.

Dintre avantajele tabelelor amintim faptul ca ele se pot

Intocmit simplu, fiind ieftine, usor de utilizat si ocupand in general un spatiu redus.

In tehnica se opereaza cu trei tipuri de tabele :

a) Tabelele calitative care stabilesc relatiile dintre marimi din punct de vedere calitativ, in tabel explicandu-se in fond narativ notiuni continute in capul de tabel.

b) Tabelele statistice pentru care unele variabile sunt exprimate cantitativ pe cand altele, care contin de obicei variabile independente nu se exprima cantitativ, din exemplul ce urmeaza rezultand structura acestor tabele.

Titlul ( Unele elemente ale sistemului solar )

c) Tabelele functionale care redau valorile corespunzatoare ale variabilei independente ( x ) si dependente ( y ) trecute una langa alta. Forma tabelei este aceeasi cu cea a tabelei statistice, avand variabila independenta trecuta in coloana de intrare. Fiecare coloana din tabela trebuie sa aiba un cap care sa dea numele si unitatea in care se exprima cantitatea respectiva.

Se recomanda ca variabila independenta sa fie o marime simpla ca timpul, presiunea, temperatura si distanta si nu o marime complexa.

Materialul explicativ, indicatia surselor si referintele se recomanda a se da in subsolul tabelei.

Unele proprietati ale hidrogenului comprimat 1)^*

1)^* Dupa lucrarea ...

Valorile lui x difera in mod obisnuit, nefiind obligatoriu ca diferenta sa fie neaparat o cantitate constanta. Este preferabil ca valorile lui y sa fie ajustabile adica valorile succesive ale lui y sa varieze gradat fata de variatiile egale succesive ale lui x pentru ca tabela sa fie cat mai intuitiva . Operatia de ajustare este asa dar obligatorie cand in cursul experimentului parametrul x nu variaza cu un pas constant.

Dupa imprejurari, ajustarea se poate face dupa unul din urmatoarele procedee :

1) luand valorile corespunzatoare dintr-o ecuatie care reprezinta datele :

y = f(x)

2) luand valorile corespunzatoare dintr-un grafic in care este trasata o curba continua ( fara franturi ) ce reprezinta datele.

3) aplicand corectiile obtinute printr-un procedeu matematic arbitrar, fiind posibile mai multe metode numerice. Una dintre metode se bazeaza pe procedeul celor mai mici patrate care presupune o valoare constanta pentru si o functie parabolica pentru y = f(x) . Metoda poate fi folosita daca pe o portiune egala cu 4 intervale se obtine o apropiere suficient de buna de relatia parabolica de tipul admis. Ecuatia de baza pentru aceasta metoda este :

( 4.1 )

unde si sunt cinci valori succesive tabelate ale lui y iar a este valoarea ajustata a lui care trebuie sa o inlocuiasca pe aceasta in tabela.

Cand se foloseste o tabela, se recurge adesea la o interpolare pentru a gasi pe y ce corespunde unui x dat, pentru valori intermediare ale lui x .

Interpolarea poate fi facuta dupa o serie de procedee, cateva dintre acestea fiind redate in cele ce urmeaza :

1) grafic, trasandu-se o curba continua adaptata la datele din tabela si apoi citind pe y de pe aceasta curba.

2) aplicand metoda partilor proportionale pentru care :

( 4.2 )

unde si sunt coordonate ale punctelor succesive tabelate astfel incat .

3) aplicand formula de interpolare a lui Gregory Newton :

( 4.3 )

in care este punctul tabelat cel mai apropiat de ( x , y ) iar .

4) utilizand metoda ecuatiei care consta in alegerea a trei puncte tabelate de coordonate si cat mai apropiate de ( x, y ), in deplasarea originii si schimbarea coordonatelor prin substitutiile :

( 4.4 )

( 4.5 )

in substituirea valorilor lui si in ecuatia sub forma de determinant

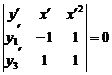( 4.6 )

in rezolvarea ei in raport cu si apoi in afara valorii lui y dupa ( 5 ).

Tabelele pot fi si extrapolate aplicand unul din procedeele de interpolare de mai sus a valorilor lui x , netabelate . Exceptand cazul cand legea care leaga pe y de x este cunoscuta, astfel de extrapolari sunt in cel mai bun caz numai aproximative. Extrapolarile ce corespund valorilor lui x care depasesc numai putin limita valorilor cuprinse intr-o tabela sunt mai sigure decat cele ce corespund valorilor care depasesc considerabil aceste limite.

5. Reprezentarea datelor prin grafice

In mod obisnuit graficele dau o legatura cantitativa intre o marime y functie de o alta marime x . Cu toate ca fenomenele fizice studiate in laborator au o desfasurare continua, prin insasi natura incercarilor nu pot fi determinate decat intermitent valorile de corespondenta dintre marimi, valori ce reprezentate intr-un sistem cartezian se pot uni printr-o curba continua.

Reprezentarea grafica a rezultatelor unor incercari cunoaste urmatoarele etape :

1) alegerea hartiei pentru grafic

2) alegerea scarilor pentru marimile reprezentate

3) marcarea diviziunii scarii pe axe si trasarea caroiajului

4) marcarea punctelor masurate

5) trasarea curbei pe baza punctelor marcate.

1) Formatul necesar reprezentarii se alege avand in vedere scopul pentru care se intocmeste graficul si precizia necesara in urmarirea fenomenului. De asemeni trebuie avuta in vedere si calitatea hartiei astfel ca aceasta sa permita corecturi si stersaturi.

2) Alegerea scarii este deosebit de importanta pentru utilitatea graficului. Se recomanda ca scara sa fie multiplu de 1, 2, 5, sau 10 al numarului de diviziuni al hartiei, alegandu-se astfel ca variatia parametrului reprezentat sa nu fie denaturata; daca scara este prea mare punctele experimentale vor fi departate si trasarea curbei este pasibila de erori; pentru scari prea mici curba va fi aplatisata, fara a se scoate in evidenta caracterul variatiei parametrului studiat.

3) Pentru marcarea diviziunilor scarii pe axele de coordonate se inscriu valorile diviziunilor pe fiecare linie sau din 2 in 2 linii principale, scrierea fiind uniforma pentru intreg graficul, in lungul axei marcandu-se marimea reprezentata precum si unitatile de masura. Pentru sublinierea diviziunilor principale cuprinse de grafic este necesar sa se traseze caroiajul diagramei.

4) Marcarea punctelor pe grafic este o operatie simpla care se va face insa foarte ingrijit. In situatia in care pe grafic se vor reprezenta mai multe variabile dependente, functie de aceiasi variabila independenta, pentru fiecare variabila dependenta se adopta un semn distinctiv (patrat, triunghi, cerc etc .) .

5) La trasarea curbelor se vor respecta urmatoarele observatii :

a) Curba trebuie sa fie continua, fara puncte de inflexiune

b) In masura exactitatii masuratorilor curba va trece prin imediata apropiere a punctelor.

c) Nu este necesar ca curba sa treaca printr-un anumit punct, cu atat mai putin prin punctele extreme.

d) Fiind un anumit grup de puncte, aproximativ jumatate din numarul lor trebuie sa se gaseasca pe o parte a curbei, iar cealalta jumatate pe partea cealalta.

e) Pentru marirea preciziei de trasare se pot uni punctele experimentale iar curba se va duce prin mijlocul lor s.a.m.d. (alte noi segmente, cu alte mijloace etc.).

Reprezentarea grafica trebuie sa fie insotita de o legenda care va contine cu necesitate denumirea caracteristicii ridicate, conditiile extreme din timpul incercarilor, numele celui ce a ridicat caracteristica, data precum si sursa datelor daca acestea nu provin din experimentul in discutie.

6. Reprezentarea datelor prin nomograme

Un grafic care reprezinta o dependenta functionala intre 3 sau mai multe variabile se numeste abac sau nomograma .

Cel mai simplu abac este abacul cartezian pentru o relatie functionala de forma

f(x,y,z) = 0 ( 6.1 )

Se considera Z ca parametru, i sedau valorile obtinandu-se pentru fiecare o curba

Fie dependenta

( 6.)

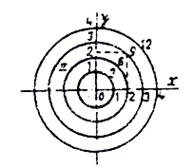
fig.1 Nomograma

Daca se ia Z ca parametru se obtin cercuri concentrice iar daca se iau X sau Y hiperbole. In fig. 1, z este parametru; daca se ia X= 2 si Z= 9 T Y= 2,5 . Uneori trasarea unui abac cartezian fiind dificila se face o transformare convenabila :

( 6.2 )

care se numeste anamorfoza, reducand ecuatia f(x,y,z) = 0 la F(X,Y,Z) = 0 ( 6.3 )

Axele si se gradeaza functional pentru citirea directa a relatiei dintre parametrii x, y si z. Scara functionala presupune gradarea unei axe diferentiat pentru o functie de o variabila ( de exemplu y= x -2 ).

Ecuatia : ( 6.4 )

Unde Z este un parametru, este o relatie functionala de tip aditional.

Prin schimbarea de variabila :

( 6.5 )

ea se transforma :

( 6.6 )

care reprezinta o familie de drepte dependente de parametrul Z .

Pentru ca nomograma sa dea direct relatia dintre X , Y si Z , axele si se gradeaza functional folosind relatiile :

( 6.7 )

Relatia de tip multiplicativ :

( 6.8 )

Se aduce prin logaritmare la forma :

( 6.9 )

Prin anamorfoza    ( 6.10 )

obtinem :

( 6.11 )

Care reprezinta o familie de drepte paralele.

Daca avem :

Nomograma avand forma din fig.2.

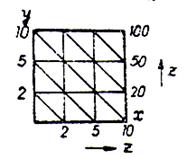
fig.2 Nomograma

7. Reprezentarea datelor prin ecuatii

7.1. Generalitati. Criteriul de verificare a oportunitatii ecuatiei alese

Datele care conduc la o curba continua, cu o alura comuna, pot fi reprezentate printr-o ecuatie ceea ce de multe ori inlesneste interpretarea si utilizarea rezultatelor masurarilor.

Problema gasirii unei ecuatii concordante cu un sir de date cuprinde in general doua etape :

1) gasirea unei forme potrivite de ecuatie care sa reprezinte datele ;

2) obtinerea unor valori adecvate pentru constantele arbitrare. In cele mai multe cazuri forma ecuatiei se cunoaste din consideratii teoretice astfel incat este necesara numai etapa a doua.

Pentru gasirea ecuatiei empirice nu exista o regula generala, putand fi numai banuita o forma convenabila dupa aspectul curbei care reprezinta datele, cateva indicatii fiind date in cele ce urmeaza :

Studiind dilatarea corpurilor, variatia unei rezistente functie de temperatura, variatia cu temperatura etc se pot intrebuinta relatii de tipul :

( 7.1 )

In general unei functii ii vom atribui o astfel de forma ori de cate ori curba care pe Y in functie de x nu difera de o linie dreapta. In caz contrar, si daca vrem sa mentinem aceasta forma, va trebui sa avem coeficienti mai multi si prin urmare vor apare termeni de ordin superior. Forma aceasta nu este practica astfel ca pentru fenomenele in care pentru valoarea lui X, Y variaza mai rapid se foloseste functia :

( 7.2 )

cum se intampla de pilda in cazul exprimarii variatiei tensiunii vaporilor saturati cu temperatura.

La alte fenomene Y variaza mult mai repede cu X , astfel ca se poate scrie :

( 7.3 )

Legea Boylle - Mariotte este reprezentata printr-o relatie de acest tip cand

b= 0 , c= 1 , Y = volum , X = p = presiune :

( 7.4 )

Pentru fenomene periodice se utilizeaza functii sinusoidala de tipul Fourier :

( 7.5 )

Exista metode sau criterii de verificare daca o anumita forma de ecuatie, adoptata este corespunzatoare, criterii ce vor fi trecute in revista mai jos :

7.1.1. Criteriul grafic de concordanta aplicabil ecuatiilor cu una sau doua constante arbitrare consta din urmatoarele :

1. Se scrie relatia presupusa, f(x, y, a, b) = 0 intr-o forma liniara in raport cu functiile alese, si care nu cuprind constantele arbitrare a si b adica :

( 7.6 )

Frecvent una dintre cele doua functii poate contine numai pe x iar cealalta numai pe y, iar noile constante A si B pot fi functii numai de a si b.

2. Se calculeaza si pentru cateva ( de exemplu pentru patru ) perechi de valori ale lui x si y mult diferite una de alta, valori alese din tabelul datelor experimentale.

Se traseaza un grafic a lui in functie de . In masura in care se obtine o dreapta, ecuatia adoptata este satisfacatoare. Verificari suplimentare pot fi efectuate luand in considerare si alte perechi de valori pentru si .

Spre exemplificare, daca datele experimentale pot fi reprezentate printr-o ecuatie de forma

( 7.7 )

De aici deducem :

( 7.8 )

In care se pune :

( 7.9 )

Reprezentand grafic pe in functie de dupa datele experimentale ( din tabel ) se verifica daca dependenta este o dreapta, neinteresand in aceasta situatie in mod expres valorile constantelor arbitrare a si b.

Tabel 7.1

Criteriul de concordanta

Δny = const (C)

Δny = C

Δny2= C

Δn(lgy) = C

Δ2y = C

Δ(lgy) = C

Δ (lgΔ y) = C

Δ(lgΔ2y) = C

Δ(lgy) = C

Δ(lgΔ y) = C

Δlny - Δlnx = C

Procedee bazate pe valoarea constanta a lui Δx , Δ(1/x) , sau Δlgx

Se calculeaza diferentele succesive de mai jos:

Δy ; Δ2y ; Δny

Δy ; Δ2y ; Δny

Δy2 ; Δ2y2 ; Δny2

Δlgy ; Δ2(lgy) ; Δn(lgy)

Δy ; Δ2y

Δ(lgy)

Δy ; lgΔy ; Δ (lgΔ y)

Δy ; Δ2y ; lgΔ2y ; Δ(lgΔ2y)

Δ(lgy)

Δy ; lgΔ y ; Δ(lgΔ y)

Δlny ; Δlnx

Se traseaza graficul apoi se intocmeste o tabela cu:

y = f(x)

y = f(1/x)

y2 = f(x)

lgy = f(x)

y = f(lgx)

lgy = f(x)

y = f(x)

y = f(x)

lgy = f(lgx)

y = f(lgx)

lny = f(x)

Forma de ecuatie adoptata

y = a+bx+cx2+.+qxn

y = a+b/x+c/x2+.+q/xn

y2 = a+bx(x2+.+qxn)

lg(y) = a+bx+cx2+.+qxn

y = a+b(lgx)+c(lgx)2

y = abx = aCb x

y = a+bcx = a+bCc'x

y = a+bx+cdx = a+bx+ced'x

y = axb

y = a+bxc

y = axCbx

Cazul

7.1.2. Criteriul tabelar de concordanta

Este aplicabil ecuatiilor cu mai mult de doua constante arbitrare. Acest procedeu depinde de ecuatia adoptata dar in general consta din :

1. Trasarea unui grafic cu date experimentale.

2. Intocmirea unei tabele dupa acest grafic.

Calcularea anumitor diferente succesive.

4. Verificarea constantei aproximative a sirului final de diferente ceea ce reprezinta un criteriu care indica daca ecuatia adoptata este adecvata sau nu. Pentru date asezate sub forma de tabela operatiile ( 1 ) si ( 2 ) nu sunt necesare. Procedeele si criteriile de verificare a celor mai multe tipuri comune de ecuatii sunt date in tab.7.1.

Diferentele succesive ce trebuie sa se obtina pot fi determinate relativ simplu. Pentru primul caz din tabela daca :

( 7.10 )

atunci

( 7.11)

si

( 7.12 )

Deoarece trebuie pastrat constant in tot timpul verificarii, relatia ( 12 ) ia forma :

( 7.13 )

Unde si sunt constante.

Repetarea procedeului de mai sus ne conduce in mod similar la :

( 7.14 )

Si in fine la

( 7.15 )

Aceasta ultima relatie indica ca daca ecuatia ( 10 ) este valabila si este mentinut constant peste tot, diferentele tabelare de ordinul trei vor fi constante . Reciproc, daca aceste diferente tabelare de ordinul trei au fost gasite constante, in limitele preciziei masuratorilor, datele pot fi reprezentate prin ecuatia (10). .

Pentru utilizarea practica a procedeului pentru cazul 7 de pilda adica se intocmeste tabelul ce urmeaza :

7.2. Procedee pentru determinarea constantelor arbitrare ce definesc ecuatiile

Pentru gasirea valorilor constantelor arbitrare exista mai multe metode. Dintre acestea, metoda celor mai mici patrate este cea mai sigura dar si cea mai laborioasa. In cele ce urmeaza vor fi trecute in revista cateva din procedeele uzuale pentru determinarea constantelor arbitrare din ecuatiile de sinteza a datelor experimentale.

7.2.1. Metoda grafica a liniei drepte pentru ecuatii cu doua constante arbitrare de tip y = a+bx .

In acest caz, dupa aducerea ecuatiei la forma de mai sus se determina dupa relatiile cunoscute :

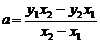( 7.16 )

Perechile de valori si , fiind coordonatele a doua puncte oarecare ale dreptei care pentru o precizie cat mai mare trebuiesc alese cat mai departate unele de altele.

Metodele corespunzatoare de prelucrare a altor ecuatii cu trei constante arbitrare si a multora cu patru constante pot fi gasite in lucrari mai complexe .

7.2.2. Metoda punctelor alese se poate folosi pentru aproape toate formele de ecuatii dar este mai adecvata pentru forme lineare sau care pot fi liniarizate in raport cu constantele lor arbitrare. Aceasta metoda este in general cea mai exacta pentru ecuatii cu trei sau mai multe constante arbitrare si este recomandabila in special cand trebuie sa se faca aproximatii succesive.

Metoda consta din urmatoarele etape :

1. Se construieste prin puncte, y in functie de x trasand o curba continua.

2. Se alege pe curba un numar de n puncte egale cu numarul constantelor arbitrare din ecuatia aleasa pentru reprezentarea datelor.

Se inlocuiesc succesiv aceste n perechi de valori ale lui x si y in ecuatia aleasa si se obtine astfel un sistem de n ecuatii cu n necunoscute. Se rezolva aceste n ecuatii simultane, determinandu-se necunoscutele adica cele n constante cautate.

7.2. Metoda mediilor se bazeaza tot pe procedeul punctelor alese, folosind o alegere a punctelor ; ea poate fi utilizata numai cand tipul de ecuatie cu care se lucreaza este liniar in raport cu constantele sale arbitrare.

Pentru ecuatia y=f(x) care contine n constante arbitrare metoda cunoaste urmatoarele etape :

1. Se impart cele N perechi de valori x si y observate in aproximativ n grupe, alegand pentru fiecare grupa numai perechile care corespund la punctele vecine pe grafic.

2. Se ia media valorilor x si y pentru fiecare grup in parte spre a obtine n perechi de valori ( x, y) .

Aceste valori medii ( x , y ) luate drept coordonate ale punctelor alese se folosesc in metoda descrisa mai sus ( 7.2.2. ) .

Rezultatele depind intrucatva de maiestria operatorului in gruparea celor N perechi de valori avand insa avantajul ca nu necesita un grafic si este mai putin laborioasa decat alte metode.

In cazurile cand ecuatia cautata este lineara sau poate fi pusa sub o forma in raport cu constantele ei arbitrare, rezultatele obtinute folosind una din metodele de mai sus se pot imbunatati prin aproximatii succesive .

Fie ecuatia : y = a +bx+cx+ . . . ( 7.17 )

Si etc. valorile constantelor arbitrare si valorile lui y calculate in prima aproximatie.

Procedeul pentru obtinerea celei de a doua aproximatii este urmatorul :

1. Se calculeaza valorile care corespund diverselor valori ale lui x .

2. Se construieste un grafic trasand daca e posibil o curba continua care sa treaca prin punctele marcate. De observat ca in acest grafic distantele punctelor pana la axa x reprezinta abaterile ecuatiei de prima aproximatie de la datele observate si ca distantele de la punctele marcate pana la curba reprezinta abaterile datelor observate de la ecuatia celei de a 2-a aproximatii, care urmeaza a fi dedusa.

Se gaseste apoi ecuatia curbei obtinute, fie prin metoda folosita la obtinerea lui y = f( x ) fie prin orice alta metoda convenabila.

4. Se aduna aceasta ecuatie de corectie la ecuatia corespunzatoare primei aproximatii spre a obtine ecuatia celei de a doua aproximatii. Pentru o noua aproximatie etapele 1-4 pot fi reluate.

7.2.4. Metoda celor mai mici patrate

7.2.4.1. Generalitati. Dintre numeroasele utilizari ale metodei celor mai mici patrate, cea mai pretioasa este determinarea constantelor arbitrare.

Sa presupunem ca un fenomen investigat experimental poate fi redat printr-o dependenta functionala de forma :

y = ax + bz + ct

Presupunem intr-o prima etapa constantele arbitrare a, b si c cunoscute. Cum x, z, t, si y se determina experimental vor fi deci supuse la erori intamplatoare. Introducand valorile x, z, t si y in diferenta y - ( ax+by+ct ) , din cauza acestor erori, rezultatul nu este zero, ci este egal cu valoarea erorii intamplatoare .

y - ( ax+bz+ct ) = ( 7.19 )

Eroarea aleatoare este mica daca masurarile s-au facut corect.

Aplicand relatia de mai sus unui sir de masurari, pentru masurarea "i" vom avea:

( 7.20 )

Diferenta este de ordinul erorilor intamplatoare si va fi cu atat mai mica cu cat a, b, c vor fi mai apropiate de valorile lor adevarate (daca masurarile au fost executate foarte ingrijit bine inteles), in acest caz trecand printr-un minim .

La calculul erorilor se demonstreaza ca trece printr-un minim in acelasi timp cu .

Putem determina pe a, b si c exprimand ca : trece printr-un minim (de aici rezultand denumirea de metoda "celor mai mici patrate "):

( 7.21 )

sau operand :

( 7.22 )

ceea ce se poate scrie si sub forma :

( 7.23 )

Vor trebui prin urmare sa se calculeze aceste sume si apoi introducandu-le in relatiile de mai sus se va obtine un singur sistem de 3 ecuatii cu 3 necunoscute din care rezulta a, b, c. Aceste ecuatii se numesc normale. Valorile a, b, c inlocuite in relatia functionala

y = ax + by + ct ne vor da tocmai forma exacta a functiei, putandu-se deci astfel reprezenta datele de observatie prin ecuatii.

Valorile lui a, b, c nu sunt absolut exacte dar admitandu-le se va comite asupra lui y eroarea medie patratica.

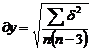( 7.24 )

7.2.4.2. Determinarea constantelor pentru linia dreapta cand variabila dependenta este supusa la erori .

Daca fenomenul investigat poate fi sintetizat printr-o ecuatie de forma :

y = a + bx

si daca presupunem ca numai variabila dependenta este supusa la erori, vom cauta sa luam pe a si b astfel ca sa fie minima, unde , reprezinta valorile observate in timpul experimentului, valori ce sunt supuse erorilor.

Daca n reprezinta numarul de puncte observate, presupunand ca toate sunt determinate cu aceiasi precizie rezulta ca mai sus :

( 7.26 )

De unde :

( 7.27 )

si in sfarsit :

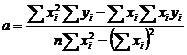( 7.28 )

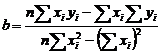
Daca prescriem ponderi diferite punctelor, adica daca acordam diferite grade de incredere diferitelor masuri ( masurarea ca " I "- a are ca ponderea ca si cand acelasi rezultat s-ar fi obtinut de ori ) parametrii ce prezinta interes vor fi :

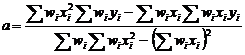( 7.29 )

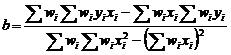
erorile probabile si ale constantelor ce intra in ecuatia unei drepte obtinuta dupa metoda celor mai mici patrate pot fi calculate in cazul a n masurari, cu ponderi egale, dupa relatiile :

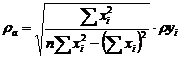( 7.30 )

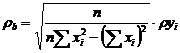( 7.31 )

in care :

( 7.32 )

7.2.4. Determinarea coeficientilor ecuatiei de tip liniar cand ambele variabile sunt supuse la erori.

Daca pentru ecuatia :

y = a + bx ( 7.33 )

ambele variabile si x si y sunt supuse la erori, se exprima mai intai x si y ca multiplii ai erorilor lor probabile.

( 7.34 )

si impartind prin a :

( 7.35 )

in care :

Daca se reprezinta la aceiasi scara pentru ambele axe dependenta , problema se reduce la gasirea dreptei pentru care U-suma patratelor distantelor punctelor pana la aceiasi dreapta - este minima. Procedand obisnuit, folosind valorile observate pentru si vor conduce la :

( 7.36 )

Din care cu conditia ca derivatele si sa fie zero si prin prelucrarea simpla a derivatelor obtinem :

( 7.37 )

si

( 7.38 )

Din (37) si (38) si tinand cont ca procesul de sumare impiedica egalarea cu zero a factorilor indicati avem :

( 7.39 )

Daca se inlocuiesc prin expresiile lor si se rezolva (39) in raport cu a avem :

( 7.40 )

Din (37) si (40) se deduce :

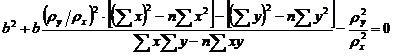( 7.41 )

Ecuatiile (40) si (41) se pot rezolva in raport cu a si b. Pentru valori ale lui mici in comparatie cu valorile lui b si a se reduc la cele consemnate prin relatiile de la numarul ( 7.29 ).

In concluzie, metoda celor mai mici patrate poate servi cu bune rezultate la calculul constantelor arbitrare din ecuatii, valorile acestora putand fi relativ rapid obtinute pentru ecuatiile liniare sau linearizabile .