Marimi caracteristice transferului de caldura

Marimi caracteristice transferului de caldura

Transferul de caldura utilizeaza o serie de notiuni care, desi sunt folosite curent si in termodinamica, hidrodinamica (convectia presupune miscarea fluidului) sau electrodinamica (radiatia presupune existenta undelor electromagnetice) su denumiri specifice.

Cele mai utilizate marimi sunt:

- campul de temperatura reprezinta totalitatea valorilor temperaturii la un moment dat t; este o functie de pozitia punctului considerat si timp:

- in coordonate plane: t = t(x,y,z,t

- in coordonate cilindrice: t = t(r,j,z,t

- in coordonate sferice: t = t(r,j y t

unde, r este raza cilindrului sau sferei, j - latitudinea punctului si y- azimutul punctului.

Functie de dependenta temperatura - timp, campul de temperatura poate fi:

- camp stationar (permanent sau constant) cand temperatura in punctul considerat are aceeasi valoare in orice moment ():

- in coordonate plane: t = t(x,y,z)

- in coordonate cilindrice: t = t(r,j,z)

- in coordonate sferice: t = t(r,j y

camp nestationar (nestabilizat sau variabil cand temperatura variaza I in timp

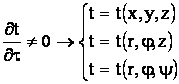
In functie de numarul de coordonate care apar, campul de temperatura poate fi:

- camp tridimensional t = (x,y,z);

- camp bidimensional t = t(x,y);

- camp unidimensional t = t(x).

In general, tehnica studiaza campurile termice stationare deoarece, in majoritatea proceselor industriale este necesara mentinerea constanta a temperaturilor. Procesul nestationar este caracteristic perioadei de punere in functiune sau oprire a unei instalatii, proceselor de incalzire, racire. Pentru un interval de timp foarte mare, teoretic infinit, procesul nestationar inceteaza.

Suprafata izoterma reprezinta totalitatea punctelor din spatiul considerat, care la momentul t au aceeasi temperatura t.

In campul termic stationar, orice suprafata izoterma isi pastreaza neschimbata forma si pozitia, adica sunt suprafete izoterme stationare, iar in campul termic nestationar o suprafata izoterma determinata isi modifica, in functie de timp, forma si pozitia, deci sunt suprafete izoterme nestationare.

Deoarece, la un moment dat, intr-un punct al campului de temperatura nu pot coexista doua temperaturi diferite, rezulta ca suprafetele izoterme nu se intersecteaza. Ele sunt suprafete inchise sau se opresc la marginea corpului.

Gradient de temperatura

Consideram doua suprafete izoterme infinit apropiate, de temperaturi t si + dt (fig.1.). Intersectand cele doua suprafete cu un plan pe o directie oarecare x, se constanta o variatie a temperaturii care, raportata la lungime are valoarea .

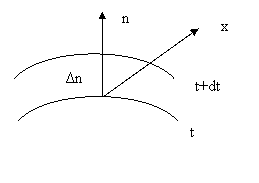
Fig.1.

Raportul maxim 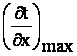apare atunci cand directia oarecare x se confunda cu normala la suprafatele izoterme:

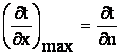(1)

In campul de temperatura variatia este modulul unui vector cu directie perpendiculara pe cele doua izoterme infinit apropiate, a carui marime este egala cu limita raportului dintre diferenta celor doua temperaturi si distanta normalei lor comune. Sensul vectorului este astfel incat el sa corespunda cresterii temperaturii. Acest vector se numeste gradientul de temperatura:

(2)

cu:    - vectorul normalei;

Ñ - operatorul nabla;

- derivata temperaturii in lungul normalei (deoarece temperatura variaza si cu timpul se considera derivata partiala).

Deci, gradientul de temperatura este un vector avand directia normala pe suprafetele izoterme, dirijat in sensul cresterii temperaturii, al carui modul este egal cu derivata in functie de distanta a temperaturii pe aceasta directie.

Valoarea gradientului de temperatura cu semn schimbat reprezinta caderea de temperatura.

Unitatea de masura a gradientului de temperatura este [K/m] sau [ C/m].

Flux de caldura (flux termic), , reprezinta cantitatea de caldura ce se transmite printr-un corp sau de la un corp la altul printr-o suprafata izoterma, S, in unitate de timp, t

[W] (3)

Fluxul termic unitar (densitatea de flux termic) q, reprezinta fluxul termic raportat la unitatea de suprafata:

[W/m²] (4)