| CATEGORII DOCUMENTE |
| Aeronautica | Comunicatii | Electronica electricitate | Merceologie | Tehnica mecanica |
Acest centru de prelucrare a fost ales pentru studiul efectuat de prezenta lucrare din urmatoarele motive:
-este un centru de prelucrare de gabarit mediu, avand cea mai larga utilizare;
mecanismul pentru schimbare automata a sculei are o constructie frecvent intalnita (foloseste un magazin de scule asezat lateral pe montant, avand axele sculelor perpendiculare pe planul de lucru al arborelui principal);

|
Figura 1 Centrul de prelucrare CPFH-500 |
Centrul de prelucrare CPFH-500 (figura 1), se afla in fabricatia S.C. Masini Unelte S.A., Bacau. Proiectul a fost realizat de catre ICSIT Titan Bucuresti, sub licenta YASUDA, Japonia, unul dintre cei mai reputati constructori de centre de prelucrare pe plan mondial.
Mecanismul pentru schimbarea automata a sculei {figura 2), cuprinde in principal:
magazinul de scule (10), amplasat lateral, solidar cu montantul;
mecanismul de transfer propriu-zis.
Parametrii tehnici ai acestui sistem sunt:
capacitatea maxima de stocare a magazinului....60 de scule;
distanta dintre axele a doua locase alaturate ale magazinului.110 mm;
greutatea maxima a sculei care poate fi manipulata....350 N;
lungimea maxima a sculelor care pot fi manipulate...400 mm;
timpul minim de schimbare al sculei (span la span)....~20 s.
Miscarile pe care le executa acest mecanism se impart in doua categorii distincte: a) miscarea de transfer, care reprezinta transportul suportului (4) pe ghidajul (3),aflat in planul orizontal situat la partea superioara a montantului. Aceasta miscare se executa de catre un mecanism plan de tip cu cilindru oscilant, actionat de motorul hidraulic liniar (MHL) (2). Suportul sustine mana mecanica propriu-zisa (6) (autooperatorul). Deplasarea se desfasoara intre cele doua pozitii de asteptare: una deasupra magazinului de scule (10), si cealalta deasupra arborelui principal (11). Miscarea are rolul de a aduce scula care urmeaza a fi folosita, in pozitia de schimbare, aflata pe verticala arborelui principal, precum si scula care a fost folosita, deasupra magazinului de scule. Acest tip de miscare nu afecteaza timpul de schimbare al sculei, intrucat se suprapune peste procesul tehnologic de aschiere;
a) miscarile pentru schimbarea propriu-zisa a sculei care inseamna:
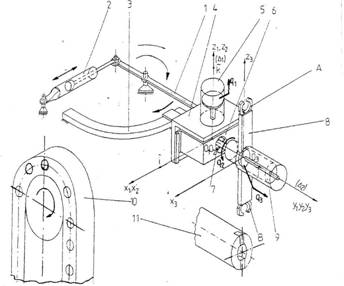
Figura 2. Mecanismul pentru schimbarea automata a sculei la centrul de prelucrare CPFH-500
miscarea pe verticala a saniei (6), in scopul pozitionarii axului uneia dintre apucatoare pe aceeasi directie cu arborelui principal sau cu cel al locasul care urmeaza a fi utilizat, din magazinul de scule. Actionarea se face cu ajutorul motorului hidraulic liniar (MHL) (5);
miscarea de rotatie cu 180 a corpului dublu-apucator (8). Actionarea este facuta de un motor hidraulic oscilant (MHO) (7);
miscarea de translatie pe orizontala a autooperatorului (9), care are drept scop extragerea si introducerea sculei din si in locasul arborelui principal ori al magazinului. Actionarea se face cu ajutorul motorului hidraulic liniar (MHL) (9).
Miscarile a si b nu se pot suprapune in timp, si deci nu se influenteaza reciproc, nici din punct de vedere cinematic si nici dinamic.
Din acesta cauza in analiza structurala vom considera ca avem doua mecanisme distincte:
mecanismul plan de tip cu cilindru oscilant (care efectueaza miscarea de transfer);
mecanismul spatial care efectueaza miscarile pentru schimbarea propriu-zisa a sculei.
Avand in vedere ca mecanismul analizat executa separat doua tipuri de miscari (de transfer si de schimbare propriu-zisa a sculei), analiza structurala va fi executata separat pentru mecanismul plan cat si pentru cel spatial.
Analiza structurala a mecanismului phr., figura 3, este caracterizata de parametrii:
n = 3 - numarul elementelor mobile;
Nm = 1 - numarul cuplelor motoare;
Pi = 4 - numarul cuplelor nemotoare;
W = 1 - gradul de mobilitate.
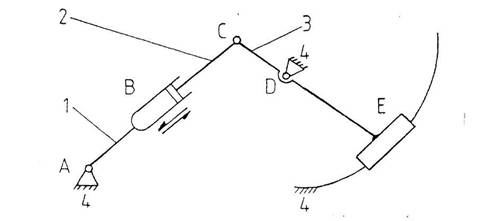
Fig. 3. Schema structurala a mecanismului plan pentru realizarea miscarii de transport a mainii mecanice
Deducem valoarea lui q (numarul de legaturi excedentare):
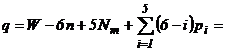
(1)
Se observa ca miscarea imprimata elementelor mecanismului ramane aceeasi daca se inlatura lantul cinematic pasiv format din ghidajul circular (4) si cupla E. Acesta introduce 5 legaturi excedentare. Din cele 8 legaturi excedentare mai raman 3 (care sunt legaturi pe contur), iar mecanismul va arata ca in figura 4.
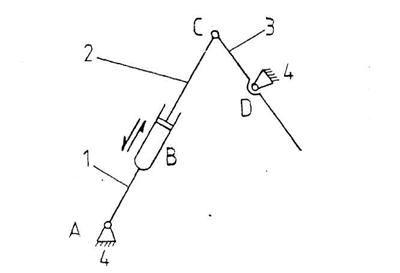
Figura 4. Schema structurala a mecanismului pentru miscarea de transport
Realizarea constructiva a mainii mecanice propriu-zise ne conduce la o prima schema structurala sub forma aratata in figura 5
Structura acestui mecanism se caracterizeaza prin:
- numarul de cuple = 6, dintre care:
a) - 4 cuple de translatie (A, B, E, si F), dintre care A si F sunt cuple motoare (puse in miscare de cilindrii hidraulici)
b) - doua cuple de rotatie, din care (C) este conducatoare
- numarul comun de
restrictii pentru elementele mobile este 3, deoarece in raport cu reperul
initial 1 (reperul baza), corpurile 2, 3 si 4 au cate trei
parametri de pozitie nuli: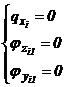
unde : - qx - parametrul de pozitie corespunzator translatiei, dupa axa Ox
- z - parametrul de pozitie corespunzator rotatiei, dupa axa Oz
- y - parametrul de pozitie corespunzator rotatiei, dupa axa Oy
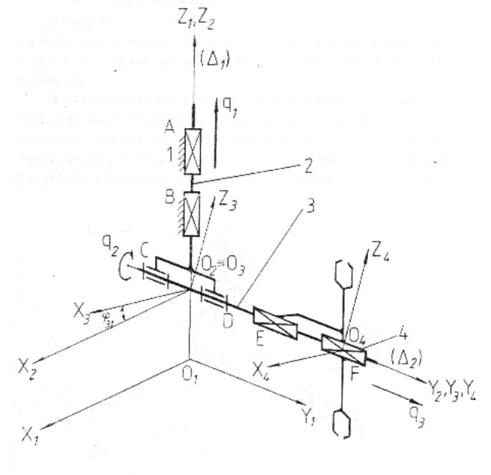
Figura 5 Schema structurala completa a mainii mecanice
Deducem valoarea lui q (numarul de legaturi excedentare):
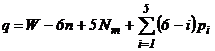 (2)
(2)
unde: W = 3 - gradul de mobilitate al mecanismului (impus prin tema de proiect)
n = 3 - numarul de elemente mobile
Nm = 3 - numarul cuplelor motoare
pi = 3 - numarul de cuple ne-motoare
i = 1 - gradul de mobilitate al cuplelor pi
Rezulta deci: q = 3 - 6 3 = 15 . Avem un numar de 15 legaturi excedentare, ceea ce corespunde la un numar de 3 cuple inferioare in plus.
Dupa cum se observa, nu exista alte legaturi excedentare deoarece mecanismul este de tip deschis simplu.
Intr-adevar, cuplele E si F, introduc acelasi tip de legaturi intre elementele 3 si 4 corespunzator conditiilor globale impuse miscarii relative, si de aceea se elimina cupla E. Acelasi lucru se intampla si cu cuplele de translatie A si B ce asigura miscarea de translatie intre elementele 2 si 1, si cu cuplele de rotatie C si D, care asigura miscarea de rotatie intre elementele 2 si 3. Prin inlaturarea cuplelor A, E si D se ajunge la structura din figura 6
Asadar, in noile conditii, datele de intrare sunt:
n = 3
Nm = 3
pi = 0
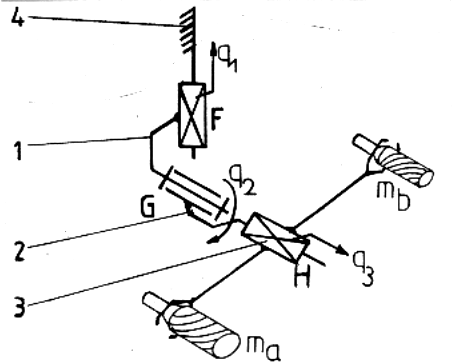
Figura 6. Schema structurala simplificata (de tipul lant deschis simplu) pentru mana mecanica la centrul de prelucrare CPFH-500
Conform relatiei (1.3), in cazul in care mecanismul se misca simultan dupa directiile tuturor gradelor de libertate, gradul de mobilitate se calculeaza astfel:
W = 6n - [5Nm - q] = 6 (3)
a) - Gradul de mobilitate astfel calculat corespunde miscarilor reale, necesare efectuarii propriu-zise schimbarii sculei
b) - Aceasta structura corespunde unei valori minime a numarului de elemente mobile in care:
n = W = Nm (4)
unde: - n - numarul de elemente mobile in raport cu elementul cinematic de referinta
- W - numarul de grade de libertate, in ipoteza in care, conditiile de legatura sunt independente
- Nm - numarul de cuple motoare
c) Acest tip de structura corespunde si conditiei de inversabilitate a modelului geometric, si anume ca pozitia sculei manipulate sa depinda de toate cele 3 coordonate generalizate (q1, q2, q3)
d) Totodata, se indeplineste si criteriul de sinteza cinematica legat de realizarea unor solutii constitutive simple, si anume, minimizarea numarului de elemente care constituie structura de manipulare, [D3], [K3], [P5].
In tehnica analizei comportarii dinamice a mecanismelor de acest tip, un rol important il ocupa modelarea comportarii dinamice.
Modelul matematic al comportarii dinamice al unui mecanism utilizat in constructia manipulatoarelor, face legatura intre torsorul fortelor si momentelor care actioneaza asupra elementelor cinematice componente si miscarea imprimata acestor elemente [D1], [M6].
Modelul dinamic al unei structuri mecanice de manipulare, este constituit din ecuatiile de miscare ale sistemului mecanic, format din elementele structurii sub actiunea fortelor exterioare.
Modelul dinamic complet, este format din modelul dinamic al structurii de manipulare si modelul dinamic al structurii de actionare.
Intrarile sistemului dinamic sunt fortele si momentele motoare, iar iesirile sunt coordonatele, vitezele si acceleratiile generalizate.
Utilizarea ecuatiilor Lagrange de speta a-II-a in analiza comportarii dinamice a MSAS, este cea mai recomandata, deoarece prezinta urmatoarele avantaje [D3], [P5], [M6], [V5],[H2], [R3]:
- elementele componente nu trebuie izolate, modelul matematic al comportarii dinamice scriindu-se fara a apela la fortele de legatura din cuple, pentru eliminarea carora ar fi fost necesare un numar suplimentar de ecuatii;
- metodele de modelare permit generarea ecuatiilor, functie de marimile de comanda aplicate sistemelor de actionare.
Modelul matematic se bazeaza pe generarea ecuatiilor Lagrange de tipul:
![]() (5)
(5)
unde: i = 1..m; m - numarul gradelor de libertate
E - energia cinetica de la nivelul intregului mecanism
qi - coordonata de pozitie relativa (sau coordonata robot)
![]() - parametrul de viteza relativa generalizata
- parametrul de viteza relativa generalizata
W - lucrul mecanic virtual
Qi - forta generalizata
Modelul matematic cuprinde un numar de ecuatii de acest tip, egal cu numarul gradelor de mobilitate ale mecanismului [O8], [U3].
Aproximari folosite:
- Fortele de frecare uscata si vascoasa nu sunt calculate explicit; valoarea lor este luata din tabele sau nomograme.
- Energia potentiala de deformatie este neglijata, considerandu-se ca variatia coordonatelor de miscare este influentata, preponderent de ceilalti parametri. In acest caz:
L= Ec.
- Modelul matematic nu tine seama de energia potentiala, determinata de fortele de greutate aplicate in originile sistemelor de coordonate, intrucat impreciziile determinate de cedarile elastice sau plastice, sunt de circa 30 de ori mai mici decat impreciziile determinate de sistemul cinematic si de conducere al structurii de manipulare.
- Metoda nu ia in calcul pozitia centrelor de greutate, forta generalizata reducandu-se in originea sistemelor de coordonate, proprii elementelor componente ale structurii.
Generarea ecuatiilor consta in principal in doua etape.
1. Realizarea modelului geometric, care cuprinde [O8], [D3], [P5], [V5] :
- realizarea schemei structurale a mecanismului mainii mecanice, in baza modelului fizic al proiectului acestuia. Acest lucru s-a realizat in subcapitolul 3.3;
- se inscrie in fiecare cupla sistemul de coordonate al elementului de intrare, in sensul parcurgerii lantului cinematic (incepand cu elementul 1), tinand cont de tipul gradului de mobilitate introdus de cupla;
- se reprezinta pe schema structurala toate elementele geometrice tip li, i ;
- se inscriu in fiecare cupla, coordonatele robot qi ;
- inscrierea pe schema structurala a fortelor generalizate, si a fortelor rezistente generalizate;
- inscrierea directiilor principale de miscare i .
In urma parcurgerii etapelor deja prezentate, a rezultat, pe baza structurii mecanismului, schema cinematica din figura 7.
2. Realizarea bilantului energetic corespunzator fiecarui grad de libertate
- determinarea energiei cinetice a intregii structuri, in ipoteza miscarii simultane pe toate axele;
- reducerea tuturor momentelor de inertie exprimate fata de alte axe decat cele care traverseaza elementul prin centrul de masa;
- calculul derivatelor totale si partiale, functie de coordonatele de pozitie, viteza si timp;
- determinarea lucrului mecanic elementar virtual;
- calculul derivatelor partiale ale lucrului mecanic virtual elementar, functie de coordonatele robot.
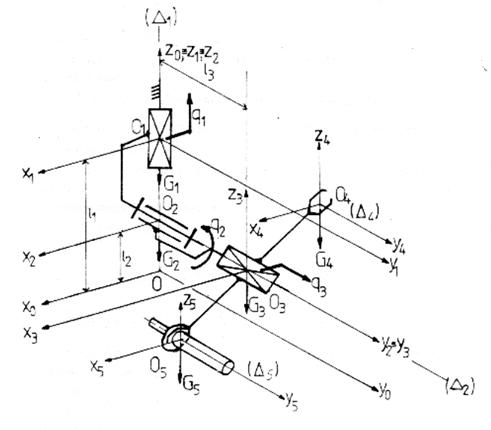
Figura 7. Modelul fizic al mainii mecanice la centrul de prelucrare CPFH-500
Modelul matematic cuprinde un numar de ecuatii egal cu numarul gradelor de libertate. In baza schemei cinematice din figura 7, se vor putea exprima energiile cinetice ale fiecarui element.
Relatiile de calcul pentru energiile cinetice pentru fiecare element, sunt :
![]() (6)
(6)
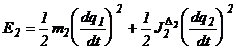 (3.7)
(3.7)
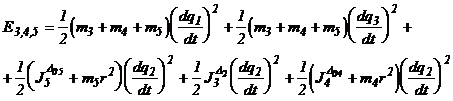 (8)
(8)
Energia cinetica totala va avea expresia :
![]() (9)
(9)
deci,
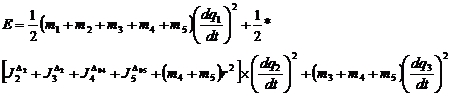
![]()
(10)
Calculul derivatelor partiale ale energiei cinetice, functie de coordonatele robot (generalizate), de ordinul 1 si 2
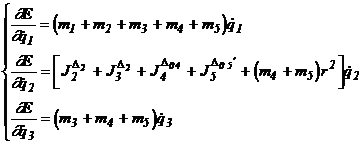 (11)
(11)
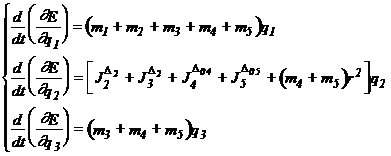 (12)
(12)
In scopul determinarii lucrului mecanic virtual elementar, vom scrie vectorii deplasarilor incrementale pentru fiecare grad de mobilitate, urmand apoi a efectua produsul scalar al vectorului activ forta-moment cu vectorii deplasarilor incrementale liniare si unghiulare.
Vectorii deplasarilor liniare si unghiulare incrementale, vor avea expresiile:
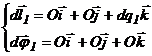 (13)
(13)
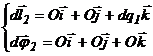 (14)
(14)
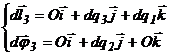 (15)
(15)
Vectorii fortei generalizate vor avea expresiile:
![]() (16)
(16)
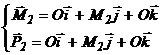 (17)
(17)
![]() (18)
(18)
Lucrul mecanic virtual elementar, se va calcula cu formula:
![]() (19)
(19)
unde, n - numarul de elemente mobile ale structurii de manipulare
Dupa efectuarea calculelor, rezulta:
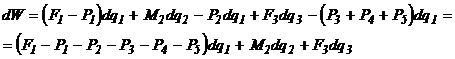 (20)
(20)
In scopul determinarii fortelor generalizate, vom calcula derivatele partiale ale lucrului mecanic virtual elementar fata de coordonatele generalizate qi.
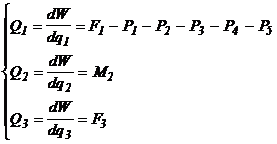 (21)
(21)
In final, modelul matematic al
comportarii dinamice a structurii mecanice a manipulatorului, va fi de
forma: 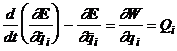 (ecuatia Lagrange de speta a-II-a), unde
(ecuatia Lagrange de speta a-II-a), unde ![]()
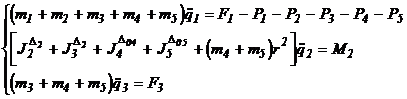 (22
(22
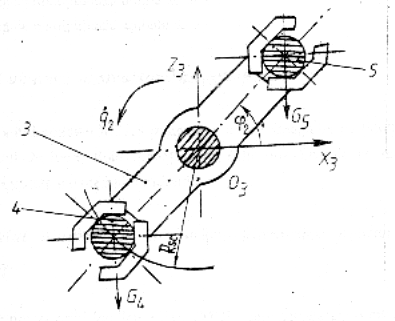
Figura 8. Actiunea momentelor rezistente suplimentare create de greutatea sculelor manipulate
Printre factorii care influenteaza in mod decisiv parametrii dinamici, se numara dezechilibrul elementului efector, cauzat de numarul si de masa variabila a sculelor de manipulat. Fenomenul este observat, in special, la elementele cu miscare de rotatie dupa o axa orizontala. Asupra acestora, actioneaza momente rezistente suplimentare care depind de pozitia lor unghiulara, (figura 8).
In general, in forma cea mai simpla, ecuatia de miscare pentru un element efector de acest tip (cu doua apucatoare), va fi :
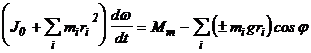 (23)
(23)
unde: J0 - momentul de inertie al elementului efector, fata de axa sa de rotatie
mi si ri
- masa, respectiv raza pozitiei centrului de masa al sculei " i ", cu ![]()
= (t) - unghiul de pozitie, curent al bratului dublu al apucatorului
Mm - momentul motor care pune in miscare elementul efector
Semnul "+" corespunde miscarii in jos a sculei, iar semnul "-" corespunde miscarii in sus.
Simularea acestui tip de miscare va face posibil sa se stabileasca efectul :
- formei constructive ale elementelor cinematice;
- distributiei maselor;
- tipului de sarcina utila (masa sculelor) asupra parametrilor de miscare si sa se traga concluzii privind modalitatile de ameliorare ale caracteristicilor dinamice ale miscarii.
In cazul MSAS pentru CPFH-500, analizat de noi, apar doua situatii :
- cand se manipuleaza o singura scula (in cazul nostru avand masa m4)
- cand se manipuleaza doua scule (avand masa m4, respectiv m5)
Tinand cont de aceste doua situatii posibile, sistemul de ecuatii (22) care descrie echilibrul dinamic al structurii mecanice, devine:
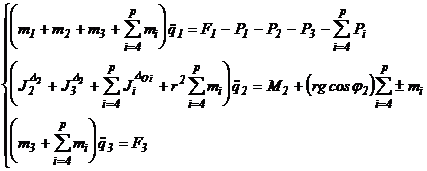 (3.24)
(3.24)
unde, p = 4, daca se manipuleaza numai scula 4
p = 5, daca se manipuleaza ambele scule (4 si 5).
Actionarea hidraulica a MSAS prezinta o serie intreaga de particularitati legate de utilizarea agentului de lucru fluid. Ecuatiile de echilibru dinamic se stabilesc in baza ecuatiilor de continuitate ale mediului hidraulic.
In cazul motoarelor hidraulice liniare (MHL) care actioneaza dupa coordonatele q1 si q3, ecuatiile care descriu functionarea in regim dinamic sunt aceleasi.
Se porneste de la ecuatiile de continuitate ale debitului, corespunzatoare actionarii pentru gradul de libertate q1 [C4], [C7], [G7], [M3], [M12].
Modelul realizat se considera a fi comandat prin debitul Q1 si perturbat de forta F (forta redusa la tija efectoare a pistonului), conform schemei bloc functionale din figura 9
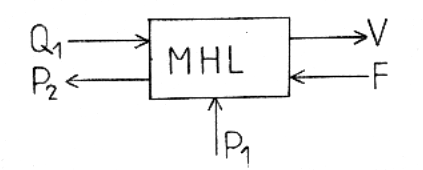
Figura Model abstract al actionarii cu motor hidraulic liniar
Totodata, se porneste de la schema de incarcare din figura 10, in care:
Q01, Q1 - debitele de intrare, respectiv de iesire [m3/s]
A01, A1 - ariile active ale pistonului, [m2]
V01, V1 - volumele instantanee ale camerei active, respectiv de iesire ale motorului, [m3]
p01, p1 - presiunile instantanee de intrare, respectiv de iesire, [N/m2].
Consideram ca debitul de intrare se distribuie in:
- debit consumat prin deplasarea
pistonului : ![]() , unde
, unde ![]() este viteza instantanee de deplasare a
pistonului;
este viteza instantanee de deplasare a
pistonului;
- debit consumat prin
compresibilitatea fluidului de lucru :![]() , relatie
derivata din legea lui Hooke;
, relatie
derivata din legea lui Hooke;
- debit consumat datorita pierderilor intre camera activa si exterior : ae p01 ;
- debit consumat datorita pierderilor (scaparilor) dintre camera activa si cea de evacuare a cilindrului si care depinde de diferenta de presiune dintre cele doua camere :
aM (p01-p1);
unde : aM , [(m3/s)/(N/m2)] coeficientul liniarizat al pierderilor de debit la piston, proportionale cu diferenta de presiune intre cele doua camere ale motorului;
ae , [(m3/s)/(N/m2)] - coeficientul liniarizat al pierderilor de debit in exteriorul cilindrului, proportionale cu presiunea in camera activa a cilindrului ;
E , [N/m2] - modulul de elasticitate al lichidului.
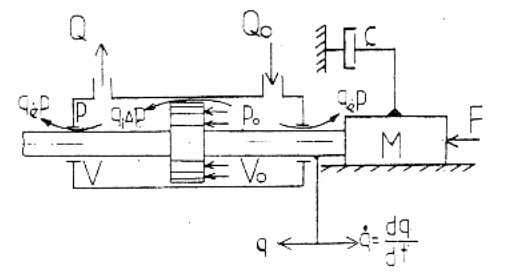
Figura 10. Schema de incarcare a motorului hidraulic liniar pentru deplasarea dupa coordonata q1
Deci, ecuatia de echilibru, in camera activa a cilindrului, va fi:
![]() (25)
(25)
Analog, ecuatia debitului din circuitul de evacuare a cilindrului va fi:
![]() (26)
(26)
Similar, ecuatiile de debit in regim dinamic, corespunzatoare actionarii hidraulice pentru gradul de libertate q3, vor fi:
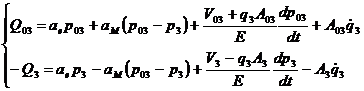 (27)
(27)
In cazul motorului hidraulic oscilant (MHO), figura 11, se considera ca forta activa Fca2 a lichidului actioneaza ca o forta concentrata in centrul suprafetei paletei oscilante [M3], [O2], [O2]. In acelasi timp, pe partea opusa, se considera ca actioneaza forta rezistenta Fcr2, de asemenea concentrata in centrul suprafetei paletei.
Din figura 11, b, rezulta ca raza centrului
suprafetei paletei este: ![]() .
.
Vom mai nota:
- deplasarea liniara (tangentiala) instantanee a centrului paletei
![]()
- viteza tangentiala a centrului paletei
![]()
Prin constructie, cursa
unghiulara a rotorului motorului este![]() .Tinand cont
de aceasta valoare, vom considera o pozitie intermediara a paletei,
si anume chiar la jumatatea cursei (
.Tinand cont
de aceasta valoare, vom considera o pozitie intermediara a paletei,
si anume chiar la jumatatea cursei (![]() ). Se obtin
astfel, volumele celor doua camere (de lucru si de evacuare), avand forma
de sector cilindric:
). Se obtin
astfel, volumele celor doua camere (de lucru si de evacuare), avand forma
de sector cilindric: 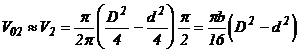
unde: - b - latimea paletei, [m]
- D - diametrul exterior al celor doua camere, [m]
- d - diametrul interior al celor doua camere, [m]
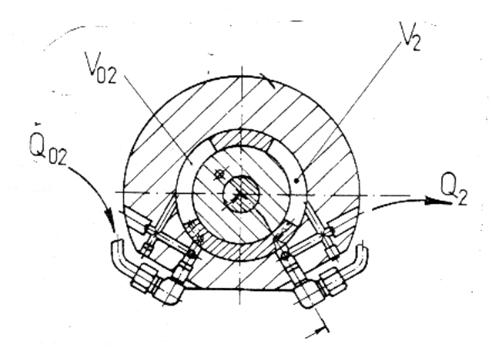
Figura 11, a
a - Sectiune prin motorul hidraulic oscilant (MHO) care actioneaza dupa coordonata q2
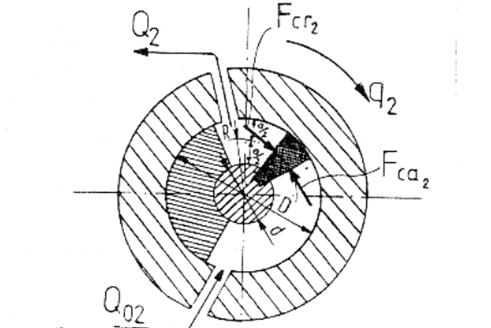
Figura 11, b
b - Schema de incarcare a MHO
De asemenea, se constata
ca ariile celor doua suprafete active ale paletei sunt egale,
avand expresia: ![]() (28)
(28)
In aceste conditii, si prin analogie cu notatiile si forma modelului matematic corespunzator gradelor de libertate q1 si q3, pentru gradul de libertate q2, modelul dinamic complet al actionarii va fi de forma:
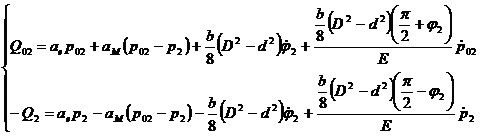 (29)
(29)
Se pleaca de la ecuatiile ideale de echilibru ale structurii mecanice - relatia 3.24- (generate prin aplicarea formalismului Lagrange). Acesta se completeaza cu termenii care caracterizeaza fortele sau momentele specifice in cazul actionarii hidraulice.
Facem observatia conform [M6], [M7], [M8], ca ecuatia de miscare, din sistemul (3.24), dupa coordonata q1, poate fi scrisa sub forma generala:
![]() (30)
(30)
Explicitand termenii pentru cazul concret al deplasarii ansamblului mecanic dupa coordonata q1, se fac urmatoarele precizari:
- mred - masa redusa la tija pistonului cilindrului hidraulic, reprezentata prin suma tuturor maselor care se deplaseaza in miscare de translatie odata cu acesta,
- ![]() - acceleratia liniara instantanee,
a ansamblului aflat in miscare;
- acceleratia liniara instantanee,
a ansamblului aflat in miscare;
-![]() - forta
motoare (redusa la tija pistonului) si care are expresia ;
- forta
motoare (redusa la tija pistonului) si care are expresia ;
![]()
- ![]() - forta
rezistenta (redusa la tija pistonului), care este compusa din:
- forta
rezistenta (redusa la tija pistonului), care este compusa din:
a) fortele de greutate Gj (j =1 5), care actioneaza cand forta motoare are aceeasi directie si sens contrar cu acestea;
b) fortele de frecare de natura vascoasa, care se opun miscarii. Ele au forma: bM q1(t), in care bM [ Ns/m] - coeficient liniar al pierderilor de forta prin frecare vascoasa a pistonului cu cilindrul hidraulic;
c) fortele de frecare uscata
(proportionala cu forta activa). Ele au forma: ![]() , unde
, unde
cfp - coeficient adimensional pentru frecare uscata;
d) Ff1(t) -forta rezistenta invinsa de motor; in cazul nostru este reprezentata prin fortele de frecare si elastice din cuple si in ghidajele saniei (6), din figura 2.
Cu aceste precizari, si avand la dispozitie si ecuatiile de continuitate ale motoarelor hidraulice in regim dinamic (3.25), (3.26), (3.27), (3.29), putem scrie ecuatiile globale de echilibru dinamic, pentru miscarile mecanismului, dupa coordonata q1:
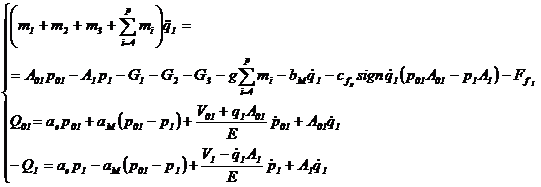
(31)
Analog, pentru miscarea dupa coordonata q3, ecuatiile globale de echilibru dinamic sunt:
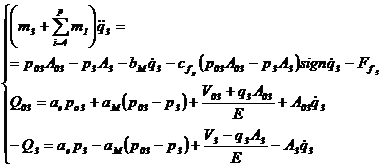 (32)
(32)
Considerand ecuatia de
miscare dupa coordonata q2 din sistemul (24) vom putea
scrie : ![]()
unde: - Jred - momentul de inertie redus la arborele motorului, al tuturor maselor solidare cu acesta, aflate in miscare de rotatie
- ![]() - acceleratia unghiulara instantanee
a tuturor maselor aflate in miscare de rotatie
- acceleratia unghiulara instantanee
a tuturor maselor aflate in miscare de rotatie
- ![]() - momentul motor
(redus la arborele motorului)
- momentul motor
(redus la arborele motorului)
- ![]() - momentul
rezistent (redus la arborele motorului)
- momentul
rezistent (redus la arborele motorului)
Din figura 11. b, momentul
motor ![]() are expresia:
are expresia:
![]() (33)
(33)
unde: - Fc a = p02 (t) A02 - forta activa concentrata in centrul suprafetei paletei motorului
- Fc r = p2 (t) A2 = p2(t) A02 - forta rezistenta concentrata in centrul suprafetei paletei motorului
- R = (D+d)/4 - raza centrului suprafetei paletei motorului
![]()
Daca exprimam cele doua arii ale
suprafetelor paletei motorului oscilant ca fiind (unde b este latimea celor
doua camere), atunci expresia (3.33) devine:
![]() se compune din :
se compune din :
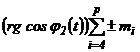
- a) momentele rezistente suplimentare create de masele
sculelor care trebuie manipulate. Acestea pot ajuta momentul motor ( au semnul
"+"), daca scula se deplaseaza in jos sau se opun miscarii
(au semnul '-'), daca se deplaseaza in sus. Din
aceasta observatie, rezulta ca acestea pot fi scrise sub
forma:
in care: p=4 daca se manipuleaza o singura scula
p=5 daca se manipuleaza doua scule simultan.
- b) momentele rezistente create de
frecarile de natura vascoasa, proportionale cu viteza ![]() , avand forma
, avand forma ![]() , unde bM 2 este coeficientul liniarizat al pierderilor
de moment;
, unde bM 2 este coeficientul liniarizat al pierderilor
de moment;
- c) momentul fortelor de frecare
uscata ( proportional cu momentul motor). Acesta este de forma: ![]() .
.
- d) momentul rezistent invins de
motor, ![]() ; in cazul nostru
este reprezentat de momentele create de fortele de frecare si
elasticitate din lagarele in care se rotesc celelalte elemente aflate in
miscare de rotatie, fiind solidare cu arborele motorului oscilant.
Astfel ecuatiile globale de echilibru dinamic pentru miscarea
dupa coordonata q2 devin:
; in cazul nostru
este reprezentat de momentele create de fortele de frecare si
elasticitate din lagarele in care se rotesc celelalte elemente aflate in
miscare de rotatie, fiind solidare cu arborele motorului oscilant.
Astfel ecuatiile globale de echilibru dinamic pentru miscarea
dupa coordonata q2 devin:
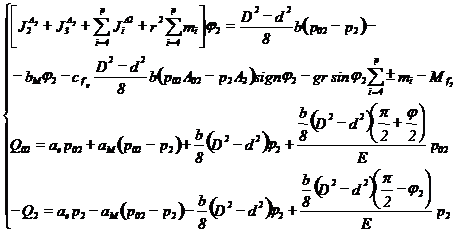 (3.34)
(3.34)
unde: p = 4, daca se manipuleaza o singura scula (4)
p = 5 , daca se manipuleaza ambele scule (4 si 5)
Realizarea modelului matematic al comportarii dinamice a MSAS a fost precedata de realizarea modelului geometric. Dupa cum s-a aratat, este indicat ca MSAS sa aiba o structura cat mai simpla, cu un numar cat mai mic de elemente. Cu prilejul intocmirii schemei structurale este necesar a fi depistate si legaturile excedentare.
Modelul matematic al comportarii dinamice propus in acest capitol este constituit din modelul dinamic al structurii mecanice, cat si din modelul dinamic al actionarii hidraulice.
Modelul dinamic al structurii mecanice a rezultat in urma folosirii ecuatiilor de tip Lagrange de speta a-II-a. Folosirea acestei metode are urmatoarele avantaje:
- elementele componente nu trebuie izolate, modelul matematic al comportarii dinamice scriindu-se fara a se apela la fortele de legatura din cuple, pentru eliminarea carora ar fi fost necesare un numar suplimentar de ecuatii;
- metoda de modelare permite generarea ecuatiilor, functie de marimile de comanda aplicate sistemelor de actionare;
De asemenea, includerea modelului dinamic al actionarii (hidraulice) in modelul dinamic complet prezinta avantajul ca tine cont de parametrii reali care intervin in functionarea acestor mecanisme:
- gradientul de pierderi de debit de lichid (intre cele doua camere ale motorului, cat si in exterior);
- influenta fortelor de frecare uscata si de natura vascoasa;
- compresibilitatea lichidului de lucru in ambele camere;
- parametrii de lucru (presiune, debit) ai instalatiei hidraulice a centrului de prelucrare.
O contributie personala este punerea in evidenta, in cadrul modelului realizat, a influentei numarului si a masei sculelor de manipulat.
In aceasta sectiune se pun in evidenta rezultatele cercetarii asistate de calculator ale comportarii dinamice a unui mecanism caracteristic pentru schimbarea automata a sculei. Rezultatele obtinute, ca urmare a cercetarii efectuate pe modelul real, pot servi si ca metoda generalizata de cercetare asistata a unor mecanisme reale similare din componenta centrelor de prelucrare. Din aceasta categorie fac parte centre de prelucrare avand urmatoarele caracteristici:
au gabarit mediu;
executa operatii de alezare, frezare si gaurire;
au magazin de scule lateral avand axele sculelor depozitate paralele cu
planul de
lucru al arborelui principal;
schimbarea sculei se face de catre un unic mecanism (nu are
mecanism intermediar
de transport).
Modelul matematic al comportarii dinamice a MSAS, reprezentat prin sistemele (31), (32), (33) sunt neliniare, deoarece contin termeni cu produs de variabile. Deoarece utilizarea unei metode pentru rezolvarea globala a sistemelor de ecuatii neliniare, este foarte dificila, este necesar sa liniarizam modelul propus. Avantajele utilizarii modelelor liniare sunt multiple. in cazul studiat, liniarizarea este necesara pentru:
a) posibilitatea de a descrie modelul propus, prin functii dinamice de transfer [M6]. Algebra functiilor de transfer cu utilizarea transformatei Laplace, este relativ simpla si pe baza ei se pot evita calculele laborioase. Trecandu-se in final de la domeniul 's' la domeniul 't', se regaseste mult mai facil originalul, al raspunsului in timp al mecanismului, la orice tip de marime de intrare;
b) utilizarea concluziilor date de teorii bine finalizate pentru sistemele de ecuatii liniare. La baza criteriilor de proiectare stau criterii de performanta cum ar fi: durata timpului de raspuns (timpul de crestere), durata timpului tranzitoriu, frecventa proprie, coeficientului de amortizare, etc.
Se pleaca de la sistemul (31), obtinut anterior, corespunzator miscarii dupa gradul de libertate q1. Vom pune in evidenta marimile:
q1 - acceleratia liniara
p01 - derivata presiunii in raport cu timpul, in camera activa a cilindrului
p1 - derivata presiunii in raport cu timpul, in camera de refulare a cilindrului hidraulic.
Pentru a elimina neliniaritatea provenita din produsul a doua variabile, se fac urmatoarele aproximari, al caror efect este neglijabil asupra modelului propus:
volumul variabil V01 + q1(t)A01 se inlocuieste cu o valoare
medie constanta ![]() - volumul mediu al
camerei (din stanga) a cilindrului.
- volumul mediu al
camerei (din stanga) a cilindrului.
volumul
variabil V1 + q1(t)A1 se inlocuieste cu o valoare
medie constanta ![]() - volumul mediu al camerei (din dreapta) a cilindrului.
- volumul mediu al camerei (din dreapta) a cilindrului.
Vj --Aj = Vo - volumul mediu al camerei de evacuare (din dreapta ) a cilindrului,
unde :
l1 - cursa pistonului, [m];
V01 - volumul initial al camerei active a cilindrului, [m ];
V1 - volumul initial al camerei de evacuare a cilindrului, [m3].
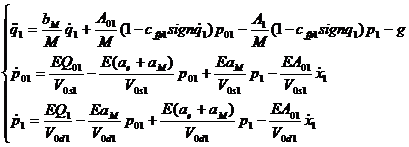 (35)
(35)
unde M=m1+m2+m3+![]() este suma tuturor maselor aflate in translatie.
este suma tuturor maselor aflate in translatie.
Se fac urmatoarele notatii:
![]()
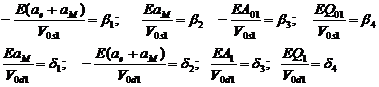 (36)
(36)
Sistemul (35) devine:
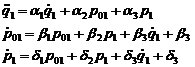 (37)
(37)
Liniarizarea ecuatiilor sistemului pentru deplasarea MSAS dupa coordonata q3 se face in mod identic ca in cazul deplasarii dupa coordonata q1, obtinandu-se un sistem de forma sistemului (37).
Analog cu cazul deplasarii dupa axa q3 , se utilizeaza functiile de transfer de forma:
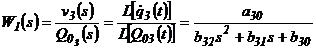 (38)
(38)
![]() (39)
(39)
Pentru acest tip de functii [C4],[O6],[O8],[O2], coeficientii functiei de transfer au expresiile aratate mai jos:
1) ![]() (40)
(40)
unde: A03 - aria activa a pistonului motorului hidraulic;
in acest caz are valoarea A03 = 28.26 [cm2]
![]() (adimensional) - coeficient de frecare
uscata (coulombian)
(adimensional) - coeficient de frecare
uscata (coulombian)
2) ![]() (41)
(41)
![]() = masa
redusa la tija motorului hidraulic a elementelor mobile. In cazul studiat:
= masa
redusa la tija motorului hidraulic a elementelor mobile. In cazul studiat:
![]()
Vm3 - capacitatea volumica a motorului hidraulic liniar;
![]()
E - modulul de elasticitate al lichidului hidraulic; in cazul studiat E=16.000 [daN/cm2]
3) ![]() (42)
(42)
unde: aM - gradientul de pierderi de debit la piston; pentru acest tip de cilindru hidraulic [B15],[B22],[O6], se alege: aM = 0,55 [(cm3/s)/(daN/cm2)]
bM - gradientul de pierderi de forta datorita fortelor de frecare de natura vascoasa, proportionale cu viteza; in cazul studiat, bM = 0,4 [daNs/cm]
4)![]() (43)
(43)
5)![]() (44)
(44)
In aceste conditii, functiile dinamice de transfer vor avea expresiile:
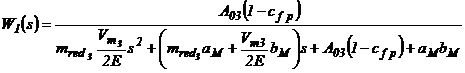 (45)
(45)
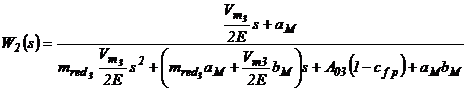 (46)
(46)
Pentru fiecare punct de functionare, se determina factorul de amortizare care are expresia:
![]() (47)
(47)
Avand datele initiale date anterior, se calculeaza o valoare = 0,41. Pentru cazul de fata, din analiza termenilor si a valorilor pe care acestea le pot parcurge, se constata ca intotdeauna < 1. In aceasta situatie,[C4],[I3],[K9],[O4], miscarea mecanismului este de tip oscilant, si se exprima prin relatia temporala de forma:
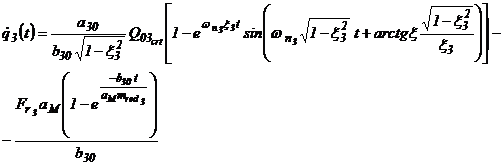
unde: - Q03, crt - valoarea curenta a debitului uleiului in conducta de alimentare, in punctul de functionare ales.
- 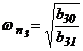 - pulsatia naturala a mecanismului
la miscarea dupa coordonata q3
- pulsatia naturala a mecanismului
la miscarea dupa coordonata q3
-Fr - forta rezistenta care trebuie
invinsa de catre motorul hidraulic liniar la demarare. Expresia ei
rezulta din prima ecuatie a sistemului (3.33) in care ![]() si
si ![]() sunt nule. Astfel:
sunt nule. Astfel:
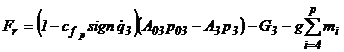 (49)
(49)
Modelarea matematica este insotita de regula atat de etapa de simulare numerica asistata, cat si de cercetare experimentala, in scopul ajustarii modelului matematic.
Simularea numerica sau analogica efectuata pe un model matematic conectat fata de modelul fizic real, scurteaza perioada de cercetare si costurile acestora, asigurand posibilitatea alegerii foarte usoare a parametrilor constructivi si functionali care sa asigure o comportare dinamica optima.
Simularea numerica se bazeaza pe rezolvarea si prelucrarea cu ajutorul calculatorului a modelului matematic obtinut in subcapitolele 5.1.1. 5.1.2. Pe baza relatiilor pentru miscarea de translatie dupa coordonata q1 , pentru miscarea de rotatie dupa coordonata q2 si (48) pentru miscarea dupa coordonata q3 , si cunoscand valoarea curenta a debitului de alimentare a fluidului Q0 (marimea aleasa de noi drept marime de intrare), se calculeaza valoarea curenta a itezei pentru primul punct de functionare.
Folosind valoarea vitezei astfel calculata, se determina valoarea curenta a acceleratiei:
![]() (50)
(50)
Valoarea curentului a spatiului va avea expresia:
![]() (51)
(51)
Calculul se reia pentru toate punctele. Numarul de puncte se determina prin aproximarea printr-un numar intreg a raportului tmax / pas , unde tmax si pas sunt respectiv, timpul maxim de studiu si pasul de iteratie, valori stabilite de catre proiectant.
Pentru celelalte puncte, acceleratia si spatiul se determina functie de valorile curente, obtinute anterior, utilizand relatiile :
![]() (52)
(52)
![]() (53)
(53)
Pe baza calculului coordonatelor tuturor punctelor, s-au determinat caracteristicile indiciale de viteza, acceleratie si spatiu .
Utilizand acest algoritm, s-a rezolvat programul de simulare numerica sub nucleul LABVIEW. Schema bloc a programului prezinta doua module importante. Primul modul rezolva ecuatiile dinamice ale modelului structurii mecanice si de actionare hidraulica a mecanismului. Cu ajutorul modulului al doilea, s-au putut determina si trasa graficele temporale pentru parametrii cinematici ai miscarii, pentru fiecare coordonata in parte, pe care le numim aici "caracteristici indiciale".
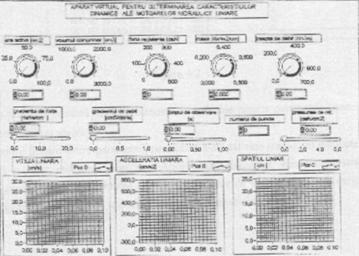
Figura 12
Asa numitul "aparat virtual" creat cu ajutorul programului LabView afiseaza in primul rand panoul frontal (de tipul celui prezentat in figura 12). Acesta este reprezentat grafic ca un aparat de la ale carui butoane sau cursoare se pot introduce datele reprezentand diverse valori pentru parametrii constructivi si functionali care influenteaza miscarea mecanismului studiat.In al doilea rand sunt afisate coloanele care cuprind toate valorile date acestor parametri in cursul experimentului - figura 13
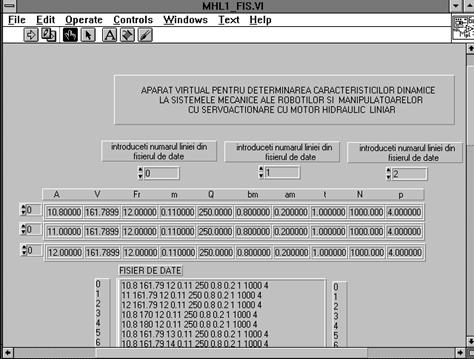
Figura 13
In final, se prezinta apoi caracteristicile indiciale pentru parametrii generalizati de viteza, acceleratie si spatiu.
Pentru fiecare dintre parametrii mentionati s-au dat cate trei valori distincte, in timp ce ceilalti au fost mentinuti constanti. Apoi s-au reprezentat simultan caracteristicile indiciale ceea ce ofera posibilitatea compararii zonelor de similitudine intre caracteristici, cat si inregistrarii informatiilor specifice care pot fi deduse din analiza acestora.
Analiza parametrilor si performantelor comportarii dinamice pe baza caracteristicilor indiciale, reprezinta de fapt analiza modului de variatie a marimii de iesire in functie de timp.
In fiecare dintre etapele
cercetarii numerice, in urma trasarii asistate a caracteristicilor
indiciale de viteza ![]() , se obtin
grafice de tipul celui aratat in figura
, se obtin
grafice de tipul celui aratat in figura
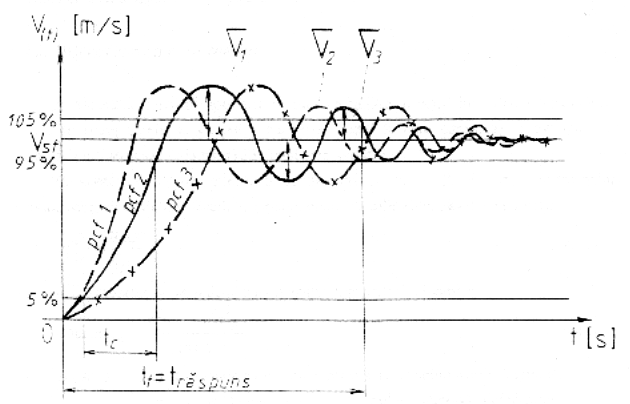
Figura 14
Se observa ca la inceperea miscarii, cresterea de viteza este aproape liniara, dupa care incepe sa oscileze in jurul unei valori stationare vst. Aceste oscilatii se autoamortizeaza si viteza devine aproximativ constanta pana in momentul inceperii franarii. Parametrii caracteristici dinamici propusi a fi studiati, si care se vor extrage din acest tip de caracteristici indiciale, sunt:
1, 3 - abaterea valorii primei, respectiv celei de a treia oscilatie fata de valoarea stationara a vitezei;
tc - timpul de crestere (timpul dupa care viteza atinge 95% din valoarea stationara) si care exprima promptitudinea mecanismului;
tt - timpul tranzitoriu (sau timpul de raspuns) - timpul dupa care viteza se stabilizeaza la o valoare care se incadreaza in 5% din valoarea stationara;
- factorul de amortizare, indicele de calitate al procesului tranzitoriu, care determina rezolvarea compromisului optim precizie-stabilitate si care este dat de relatia:
![]() (54)
(54)
Totodata, se observa ca la modificarea unui parametru constructiv functional "pcf", in conditiile in care restul parametrilor sunt mentinuti constanti, se obtin caracteristici indiciale de viteza diferite - vezi figura 14.
In scopul studierii comportarii dinamice a MSAS, o etapa importanta o constituie analiza in urma careia se va putea cunoaste modul in care parametrii constructivi si functionali influenteaza parametrii dinamici caracteristici.
In acest scop, vom introduce coeficientii de influenta ai variatiei diversilor parametri constructivi-functionali asupra parametrilor calitativ-dinamici, cu relatia:
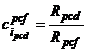 (55)
(55)
unde: Rpcd - raportul de variatie al parametrului comportarii dinamice.
Deci,![]() (56)
(56)
in care : pcdin - valoarea initiala a parametrului comportarii dinamice;
pcdfin - valoarea finala a parametrului comportarii dinamice.
De asemenea, vom defini :
Rpcf - raportul de variatie al parametrului constructiv-functional.
Deci, ![]() (57)
(57)
in care : pcfin - valoarea initiala a parametrului constructiv-functional;
pcffin - valoarea finala a parametrului constructiv-functional.
Acesti coeficienti dau o apreciere valorica, sintetica asupra masurii in care variatia unui parametru constructiv-dinamic influenteaza diversi parametri ai comportarii dinamice.
In proiectare insa nu intereseaza numai un anumit parametru sau o anumita performanta a MSAS, ci un set de performante. De exemplu, ne intereseaza ca mecanismul sa fie foarte prompt, precis si stabil. Dupa cum se observa, unele dintre aceste performante se exclud reciproc.
Deci chiar daca am determinat anterior, in cadrul etapei de analiza, modul in care parametrii constructiv-functionali influenteaza comportarea dinamica, va fi destul de greu sa se determine valoarea acestora, in asa fel incat sa fie realizate performantele dorite.
De aceea, pentru a obtine o varianta care sa fie cea mai apropiata de functionarea optima din punct de vedere dinamic a mecanismului analizat, vom face o apreciere multicriteriala asupra parametrilor caracteristici dinamici.
In acest subcapitol vom urmari influenta asupra comportarii dinamice a mecanismelor de schimbare automata a sculelor a parametrilor functionali ai motorului hidraulic liniar, cat si ai structurii mecanice.
In cadrul acestui subcapitol, s-au luat in considerare influentele:
- masei reduse mred 1;
- fortei rezistente Fr 1;
- gradientului pierderilor de forta bM 1.
a) Influenta masei reduse, mred
mred - masa intregului ansamblu, redusa la tija pistonului motorului hidraulic... [daN s2/cm]
Valoarea acesteia se compune din masa tuturor elementelor structurii mecanice, cat si din masa sculelor de manipulat. Deci :
mred =mp + melem + mscule (unde mp = masa tijei pistonului) (58)
In primul caz se considera ca se manipuleaza o singura scula, usoara, cu masa de 1 kg. In al doilea caz, se considera ca se manipuleaza doua scule de cate 20 kg fiecare; totodata se considera si o valoare intermediara, mscule 20 kg. Cu aceste valori, din (4.33) se obtine mred [daN s2/cm]. Pastrand toti ceilalti parametri constructiv - functionali constanti, se obtin caracteristicile indiciale din figura .
Raportul de variatie al masei reduse se determina asa cum s-a aratat :
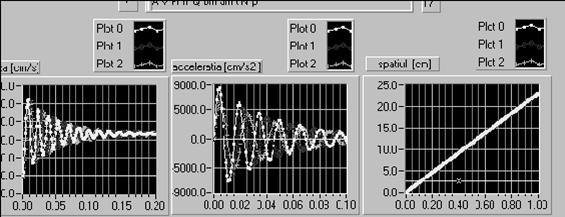
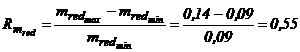
Figura 15
Din analiza caracteristicilor
indiciale rezulta rapoartele de variatie ale parametrilor
caracteristici si dinamici cat si coeficientii de
influenta,![]() .
.
Asadar, obtinem :
- timpul de crestere, sub influenta variatiei masei, ![]() si
coeficientul de influenta a masei reduse asupra timpului de
crestere,
si
coeficientul de influenta a masei reduse asupra timpului de
crestere, ![]() ;
;
- timpul fazei tranzitorii, sub influenta variatiei masei, ![]() si
coeficientul de influenta a masei reduse asupra timpului tranzitoriu,
si
coeficientul de influenta a masei reduse asupra timpului tranzitoriu,
![]() ;
;
- factorul de amortizare al fazei
tranzitorii, sub influenta variatiei masei, ![]() si
coeficientul de influenta a masei reduse asupra factorului de
amortizare,
si
coeficientul de influenta a masei reduse asupra factorului de
amortizare, ![]() ;
;
- frecventa proprie a fazei
tranzitorii, sub influenta variatiei masei, ![]() si
coeficientul de influenta a masei reduse asupra frecventei
proprii a fazei tranzitorii,
si
coeficientul de influenta a masei reduse asupra frecventei
proprii a fazei tranzitorii, ![]() ;
;
- valoarea maxima a acceleratiei, ![]() .
.
Valorile obtinute sunt concretizate in tabelul 1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabelul 1
b) Influenta fortei rezistente Fr
In cazul manipulatoarelor de tip MSAS, forta rezistenta la miscarea de translatie pe verticala, este data doar de fortele de frecare uscata (coulumbiene). Acestea depind pe de o parte de marimea fortei active (forta dezvoltata de tija pistonului motorului hidraulic), iar pe de alta parte depind de:
- solutia constructiva aleasa pentru etansarea pistonului si a tijei sale, care influenteaza tipul si marimea fortei de frecare uscata;
- frecarile care apar in elementele de ghidare ale mecanismului;
- masa sculelor de manipulat;
- forta activa furnizata de motorul hidraulic.
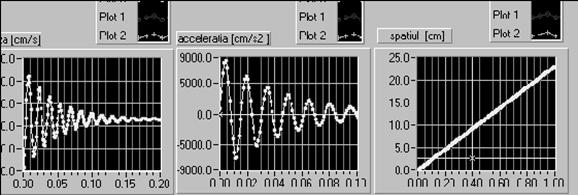
Conform literaturii de specialitate din domeniu [B14],
[B15], [L6], [V1] pentru acest mecanism se apreciaza ca forta
rezistenta Fr [daN], poate lua in cazul nostru valorile FrI{55 ; 85
; 110} [daN]
Figura 16
Corespunzator acestora, cu ajutorul programului LabView, se obtin caracteristicile indiciale din figura 16. Se calculeaza raportul de variatie al fortei rezistente :
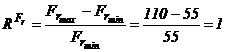
Din analiza caracteristicilor
indiciale, rezulta rapoartele de variatie a parametrilor
caracteristici dinamici cat si coeficientii de influenta![]() care sunt
prezentati in tabelul 4.2
care sunt
prezentati in tabelul 4.2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabelul 2
c) Influenta gradientului de forta bM
bM [daN s/cm], se mai numeste si coeficient al pierderilor de forta, proportionale cu viteza elementelor aflate in miscare. Aceste pierderi se datoreaza frecarilor de natura vascoasa, dintre piston si cilindru. Ele depind de vascozitatea si densitatea agentului hidraulic sau a lubrifiantului elementelor de ghidare, [B22],[K7],[K9],[O2],[V1].
In cazul MSAS studiat, pentru bM se adopta valorile bM I [daN s/cm]
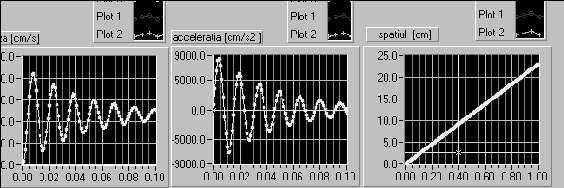
Figura 17
Corespunzator acestora, cu ajutorul programului LabView, se obtin caracteristicile indiciale din figura 17. Se calculeaza raportul de variatie al gradientului de forta :
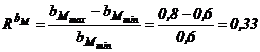
Din analiza caracteristicilor
indiciale rezulta rapoartele de variatie a parametrilor
caracteristici dinamici cat si coeficientii de influenta![]() care sunt
prezentati in tabelul 3
care sunt
prezentati in tabelul 3
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tabelul 3
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2402
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved