| CATEGORII DOCUMENTE |
| Agricultura | Asigurari | Comert | Confectii | Contabilitate | Contracte | Economie |
| Transporturi | Turism | Zootehnie |
Determinarea ritmului optim al aprovizionarii
Un agent economic desfasoara o activitate , pentru care se aprovizioneaza cu
anumit produs omogen.
Ipoteze si notatii :
- notam prin T perioada contractata a activitatii respective , masurata in zile ;
- prin Q vom nota cantitatea de produs necesara pe intreaga perioada T ;
- precizare : agentul economic este obligat sa se aprovizioneze cu intreaga
cantitate Q : el are insa libertatea sa decida de cate ori se va reaproviziona pe parcursul perioadei gestiunii .
- in cazul mai multor reaprovizionari , acestea vor fi facute : cu cantitati
egale, la intervale de timp egale .
- activitatea este dimensionata de un sistem de costuri : in cadrul acestei
variante , vom folosi urmatoarele :
- costul de lansare a comenzii , notat prin C1 : acest cost nu
depinde de marimea comenzii ( deci se masoara in lei/comanda) ;
- costul unitar de stocare , notat C2 :acesta este costul platit pentru a pastra o unitate de produs in stoc , de-alungul unei unitati de timp : se masoara , de exemplu , in lei/kg.x zi .
- stocul initial se consuma cu viteza constanta , deci cantitatile consumate sunt
proportionale cu timpul ; in cazul acestui model , nu vom admite lipsa de stoc ( adica nu vor exista perioade in care stocul sa fie negativ ).
Graficul evolutiei nivelului stocului :
- a: cazul in care agentul economic se aprovizioneaza o singura data , la inceputul perioadei gestiunii , cu intregul necesar pe acea perioada
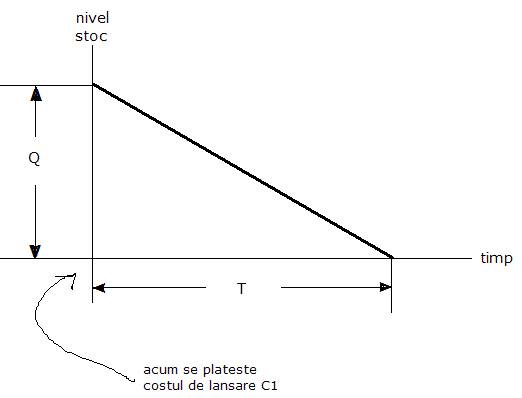
In acest caz , costul gestiunii se va compune din :
- costul lansarii comenzii , anume C1 ;
- costul stocarii celor Q unitati de produs, timp de T zile , cu C2 lei
pe zi pentru o unitate :
Deoarece nivelul stocului scade in timp , ajungand in final la zero, si deci cheltuielile de stocare fiind din zi in zi mai mici , acest cost se aplica la stocul mediu Q /2 : asadar, cheltuielile totale de stocare vor fi
![]() ,
,
deci costul total al gestiunii va fi :
![]()
Observare : nu se pune problema optimizarii acestui cost , deoarece nu dispunem de parametru variabil care sa influenteze costul.
- b: in cazul in care agentul economic se aprovizioneaza de mai multe ori in decursul perioadei T :
Vom nota prin "n" numarul de reaprovizionari : atunci evident ca fiecare reaprovizionare se face cu cantitatea Q /n , iar intervalul de timp dintre doua reaprovizionari va fi egal cu T /n .
In continuare este prezentat graficul evolutiei nivelului stocului in acest caz ( in desen s-a folosit varianta n = 3 ):
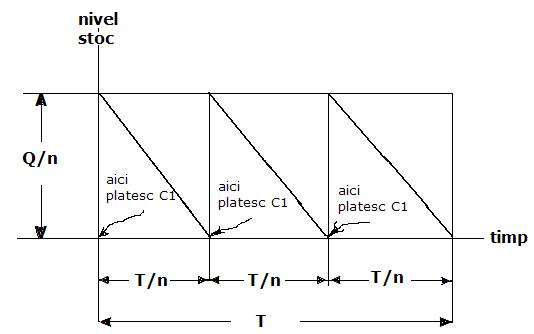
Asadar :
- costul de lansare al comenzii se plateste la inceputul fiecarei subperioade ,
deci cheltuiala totala cu lansarea comenzilor va fi
F1 = n∙C1 ;
- intr-o subperioada
: pastrez in stoc , in medie , cantitatea ![]() , timp de
, timp de
![]() zile , cu costul de C2 lei / kg. x zi , deci in total :
zile , cu costul de C2 lei / kg. x zi , deci in total :
![]()
- pe intreaga perioada T , acest cost este platit de "n" ori, deci totalul cheltuielilor de stocare va fi
![]()
In final, cheltuielile de gestiune vor fi :
![]() .
.
A determina gestiunea optima revine la a determina valoarea lui "n" pentru care functia F(n) ia cea mai mica valoare .
Intrucat variabila "n" este un numar intreg , vom fi obligati ca in acest scop sa folosim principiul combinatorial .
Principiul combinatorial : valoarea parametrului intreg "n" pentru care functia F(n)
atinge valoarea maxima este solutia sistemului
![]()
La noi :
- ![]()
- ![]() : din relatia F(n) ≥
F(n-1) gasim
: din relatia F(n) ≥
F(n-1) gasim
![]() ( relatia
1)
( relatia
1)
- ![]() din relatia F(n) ≥ F(n+1)
gasim
din relatia F(n) ≥ F(n+1)
gasim
![]() (
relatia 2) .
(
relatia 2) .
Prelucrarea relatiei (1):
![]()
Notand ![]() , gasim :
, gasim : ![]() ,
,
asadar ![]() ( relatia 3)
( relatia 3)
== // ==
Prelucrarea relatiei (2):
![]()
asadar
![]() ( relatia
4);
( relatia
4);
Din relatiile ( 3 ) si (4) gasim :
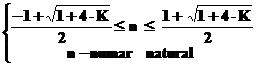
Observare
: acest sistem are cel
putin o solutie, indiferent de datele problemei : in cazul
in care ambele numere ![]() sunt naturale,
atunci ambele sunt solutii optime ale problemei de aprovizionare .
sunt naturale,
atunci ambele sunt solutii optime ale problemei de aprovizionare .
END
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1737
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved