Fluxuri maxime in retele - Notiuni introductive

Fluxuri maxime in retele - Notiuni introductive

Fie un digraf definit prin multimea cu noduri si multimea

cu arce. Se definesc functiile : capacitate margine inferioara si functia valoare . Capacitatea , a arcului din A, desemneaza cantitatea maxima care poate traversa arcul, marginea inferioara , a arcului din A , desemneaza cantitatea minima care poate traversa arcul si numarul desemneaza valoarea nodului . Problema fluxului in reteaua consta in a determina functia flux care verifica constrangerile :

(2.1.a)

(2.1.b)

unde

In forma matriceala, problema fluxului in reteaua se reprezinta in modul urmator :

(2.2.a)

(2.2.b)

cu vectori coloana. In aceasta formulare , este matricea de incidenta nod-arc care este o matrice . Fiecare coloana din matrice corespunde arcului . Coloana are un +1 in linia corespunzatoare nodului , un -1 in linia corespunzatoare nodului si restul elementelor sunt zero.

Constrangerile (2.1.a) se numesc constrangerile de conservare a fluxului. Primul termen al constrangerii corespunzatoare nodului reprezinta fluxul total de iesire din nodul si termenul al doilea reprezinta fluxul total de intrare in nodul ; daca , atunci nodul este nod sursa; daca , atunci nodul este nod stoc; daca , atunci nodul este nod de transfer.

Constrangerile (2.1.b) se numesc constrangerile de marginire a fluxului.

In problema (2.1) inlocuim variabila prin si obtinem problema:

(2.3.a)

(2.3.b)

unde

Deci problema fluxului cu margini inferioare pozitive se poate transforma intr-o problema cu margini inferioare zero. De aceea, in continuare consideram fara a restrange generalitatea, altfel spus consideram problema fluxului in reteaua .

In multimea fluxurilor se introduc relatia de ordine partiala si operatia de adunare (scadere). Presupunem ca multimea arcelor este ordonata dupa o anumita ordine.

Definitia 2.1 : Fie si doua fluxuri in reteaua . Se spune ca fluxul este mai mic decat fluxul si scriem daca pentru si exista cel putin un arc astfel incat . Se spune ca este suma fluxurilor si daca pentru . Analog se defineste .

Cele mai simple fluxuri nenule in reteaua sunt fluxul de-a lungul unui drum elementar de la un nod sursa la un nod stoc si fluxul de-a lungul unui circuit elementar . Aceste fluxuri se definesc in modul urmator :

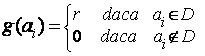
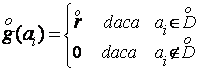
Definitia 2.2 : Un flux in reteaua se numeste flux elementar daca sau .

Fie multimea drumurilor de la nodurile sursa la nodurile stoc si multimea circuitelor in reteaua . Un flux in reteaua poate fi definit in doua moduri : putem defini fluxurile pe arce si putem defini fluxurile elementare pe drumuri si circuite. In formularea flux arc variabilele sunt fluxurile care verifica constrangerile (2.1). In formularea drum-circuit variabilele sunt fluxurile elementare si .

Orice flux nenul in formularea arc se poate descompune in fluxuri elementare din formularea drum-circuit, asa cum arata urmatoare teorema.

Teorema 2.1 . (Teorema descompunerii fluxului) . Fiecare flux drum-circuit poate fi reprezentat unic ca un flux arc. Invers, fiecare flux arc poate fi reprezentat (nu necesar unic) ca un flux drum-circuit cu urmatoarele doua proprietati:

(a)  fiecare drum cu flux nenul conecteaza un nod sursa la un nod stoc;

(b)  cel mult drumuri si circuite au flux nenul ; dintre acestea cel mult circuite au flux nenul.

Demonstratie : Pentru afirmatia directa definim :

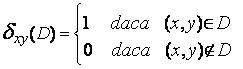
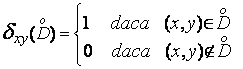
Pentru fiecare arc definim :

.

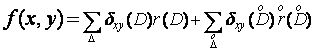Astfel fiecare flux drum-circuit determina fluxul arc unic.

Pentru afirmatia inversa se da o demonstratie algoritmica pentru a arata cum descompunem un flux arc in fluxuri elementare. Algoritmul este urmatorul :

PROGRAM DESCOMPUNERE-FLUX;

BEGIN

WHILE DO

BEGIN

IF exista nod sursa

THEN BEGIN

se selecteaza un nod sursa

END

ELSE BEGIN

se determina in arc cu ;

END;

WHILE nu este nod stoc DO

BEGIN

se determina un arc cu ;

IF

THEN

ELSE EXIT

END;

IF este nod stoc

THEN BEGIN

FOR DO

IF

THEN

ELSE ;

END;

ELSE BEGIN

FOR DO

IF

THEN

ELSE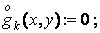

END;

END;

END.

Initial algoritmul porneste cu . Cat timp si exista nod sursa atunci algoritmul determina fie un flux drum , fie un circuit . Cat timp si nu exista nod sursa atunci algoritmul determina un flux circuit . Se observa ca de fiecare data cand se determina un flux drum , valoarea a unui nod devine zero sau fluxul pe anumite arce devine zero si de fiecare data cand se determina un flux circuit , reducem fluxul pe anumite arce la zero. Prin urmare dupa un numar finit de iteratii nu mai exista noduri cu si . Deci algoritmul este convergent si este evident ca, la terminarea algoritmului, fluxul originar este suma fluxurilor pe drumurile si circuitele identificate in timpul executiei algoritmului. De asemenea, rezulta din cele spuse mai sus ca reprezentarea drum-circuit a fluxului dat contine cel mult drumuri si circuite cu flux nenul si dintre acestea cel mai mult circuite au flux nenul.

Sa consideram un flux cu pentru toate nodurile din . Un astfel de flux se numeste circulatie.

Teorema 2.2. (Teorema descompunerii circulatiei). Oricare circulatie poate fi reprezentata ca flux circuit de-a lungul a cel mult circuite cu flux nenul.

Demonstratie : Daca pentru toate nodurile din , atunci algoritmul descompunerii fluxului determina la fiecare iteratie un flux circuit si conform Teoremei 2.1, cel mult circuite au flux nenul.

Teorema 2.3. (Teorema de complexitate a algoritmului descompunerii fluxului).

Algoritmul descompunerii fluxului are complexitatea .

Demonstratie : Algoritmul executa cel mult iteratii. Complexitatea oricarei iteratii este . Deci algoritmul are complexitatea .

Daca se utilizeaza o structura de date adecvata si se fac unele modificari in algoritm atunci complexitatea algoritmului scade la .

Exemplul 2.1. Sa ilustram algoritmul descompunerii fluxului pentru fluxul din reteaua reprezentata in figura de mai jos :

.desen pagina 91.

Deci

si .

Initial . Daca algoritmul selecteaza nodul sursa si determina drumul si , atunci si . La urmatoarea iteratie algoritmul selecteaza nodul sursa 5 si determina drumul cu , atunci . In a treia iteratie nu mai exista noduri sursa () si presupunem ca algoritmul determina arcul cu si circuitul cu .

Atunci si algoritmul se termina. Aceasta descompunere nu este unica.

Fie multimea nodurilor sursa, multimea nodurilor stoc si multimea nodurilor de transfer (intermediare). Valoarea fluxului de la la este

Daca multimea nodurilor sursa are un singur nod il notam cu si daca multimea nodurilor stoc are un singur nod il notam cu . Evident ca .

Problema fluxului maxim de la nodurile sursa la nodurile stoc in reteaua consta in a determina functia flux care verifica constrangerile :

Maximizeaza (2.4.a)

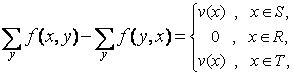(2.4.b)

(2.4.c)

Problema fluxului maxim de la nodul sursa la nodul stoc consta in a determina functia flux care verifica constrangerile :

Maximizeaza (2.5.a)

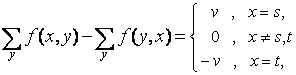(2.5.b)

(2.5.c)

In acest caz am considerat si .

Se construieste reteaua extinsa plecand de la reteaua in modul urmator :

Teorema 2.4. (Caracterizarea problemei fluxului intr-o retea cu surse si stocuri multiple). Problema fluxului maxim de la la in reteaua este echivalenta cu problema fluxului maxim de la la in reteaua .

Demonstratie: Daca este un flux maxim cu valoarea de la la in reteaua , atunci se poate defini aplicatia in modul urmator :

Astfel verifica constrangerile

Maximizeaza

.

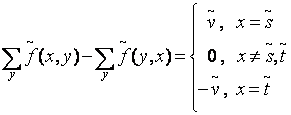
cu . Rezulta ca este un flux maxim in reteaua .

Reciproc , daca este un flux maxim de valoare in reteaua , atunci restrictia sa este evident un flux maxim cu valoarea in reteaua .

Problema determinarii unui flux care verifica (2.4.b) si (2.4.c) cu valorile precizate se numeste problema ofertei si cererii. In acest caz un nod se numeste nod oferta si un nod se numeste nod cerere.

In cazul problemei ofertei si cererii se construieste reteaua extinsa plecand de la reteaua , cu multimea nodurilor oferta si multimea nodurilor cerere, ca mai sus, cu deosebirea ca functia capacitate se defineste in modul urmator :

Un arc cu proprietatea ca se va numi arc saturat .

Teorema 2.5. (Caracterizarea problemei oferta-cerere). In reteaua exista un flux care verifica (2.4.b) si (2.4.c) daca si numai daca in reteaua exista un flux maxim care satureaza toate arcele din si .

Demonstratie: Se demonstreaza analog ca Teorema 2.4.

Exemplul 2.2. Se considera reteaua din figura 2.2, unde , , si pe fiecare arc s-a trecut capacitatea.

Reteaua extinsa este reprezentata in figura 2.3, unde , . Fluxul maxim , reprezentat de primul numar de pe fiecare arc al retelei , satureaza arcele din si . Deci problema oferta-cerere are solutie si este restrictia functiei flux la multimea .