Notiuni de baza in teoria grafurilor

Notiuni de baza in teoria grafurilor

Definitie:

Se numeste graf orientat un triplet G = (N, A, g) format dintr-o :

-> multime N de elemente numite noduri sau varfuri

-> familie A de elemente numite arce

-> aplicatie g: A→ N N numita functie de incidenta, prin care fiecarui element aA i se asociaza o pereche ordonata (x, y) N N cu x ≠ y ; daca eliminam conditia x ≠ y atunci arcul de forma (x, x) se numeste bucla, iar G se numeste graf general orientat.

In continuare vom presupune ca graful orientat G este finit, adica multimea nodurilor N= este finita si familia arcelor

A= este un sir finit.

Cardinalul multimii N , notat | N | = n , se numeste ordinul grafului orientat G .

Un graf orientat G = ( N, A, g ) se reprezinta grafic in modul urmator :

-> fiecare nod xN se reprezinta printr-un punct sau cerculet in plan ;

-> fiecare arc aA, a= (x, y) se reprezinta printr-o linie care uneste cele doua noduri si pe care se afla o sageata cu sensul de la x la y.

Exemplu: Graful din figura de mai jos este de ordinul 8.

Figura 1.1.:

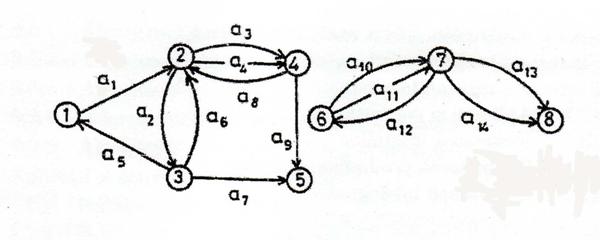
Observatie: Reprezentarea grafica a unui graf orientat G = ( N, A, g) nu este unica. In primul rand nodurile se pot plasa in plan la intamplare. In al doilea rand nu este obligatoriu ca arcele sa fie segmente de dreapta.

Exemplu : Cele trei grafuri din figura 1.2. reprezinta acelasi graf .

Figura 1.2.:

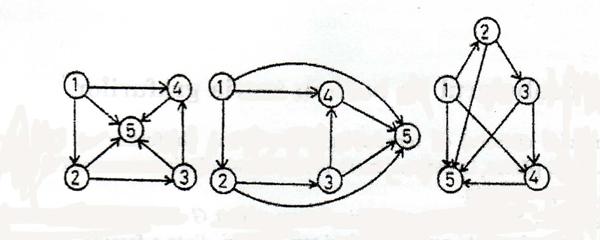
Definitie: Doua grafuri orientate, = ( ,, ) si = (, , ) se numesc izomorfe, daca exista o bijectie Φ : → cu proprietatea ca aplicatia ψ : → , definita prin ψ( x , y ) = (Φ(x ), Φ(y )) , (x , y ) A , (Φ(x ), Φ(y )) A , este o bijectie.

Exemplu: Grafurile G = ( N , A , g ) si G = ( N , A , g prezentate in figura de mai jos sunt izomorfe.

Figura 1.3.:

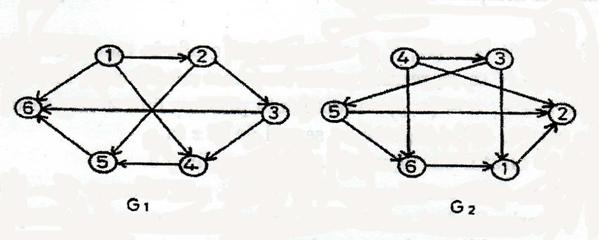
Daca definim bijectia Φ prin Φ(1) = 4, Φ(3) = 5, Φ(4) = 6, Φ(5) = 1, Φ(6) = 2, atunci ψ(1, 2) = (Φ(1),Φ(2)) = (4, 3) , ψ(1, 4) = (Φ(1),Φ(4)) = (4, 6) , ψ(1, 6) = (Φ(1),Φ(6)) = (4, 2) etc. este evident bijectia ψ : A → A

Definitie: Daca oricare pereche ordonata (x, y)NN este imaginea a cel mult q, q > 1, elemente din A, atunci G = ( N, A, g) se numeste multigraf orientat.

Exemplu: In figura 1.1. avem un multigraf orientat cu q = 2.

In paragrafele si capitolele urmatoare ne vom ocupa de grafuri orientate cu q = 1. In acest caz functia g este injectiva si familia A este o multime. Un astfel de graf se numeste digraf si de noteaza G = ( N, A).

Definitie: Se numeste graf neorientat un triplet G = ( N, A, g) format dintr-o multime N de elemente numite noduri sau varfuri, dintr-o familie A de elemente numite muchii si dintr-o aplicatie g : A → P (N) numita functie de incidenta, prin care fiecarui element a A i se asociaza o pereche P (N); daca consideram g : A → P (N) , unde P (N) = P (N) U P (N) , atunci aplicatia g asociaza fiecarui element a A, fie o pereche de noduri P (N) care se noteaza [x, y] sau [y, x], fie un nod P (N) care se noteaza [x, x] si se numeste bucla, iar G se numeste graf general neorientat.

In continuare vom presupune ca graful neorientat G este finit, adica multimea nodurilor N este finita si familia muchiilor A este un sir finit.

Un graf neorientat G = ( N, A, g) se reprezinta grafic la fel ca in cazul grafurilor orientate cu deosebirea ca o muchie a = [x, y] se reprezinta printr-o linie care uneste cele doua noduri fara sageata care precizeaza sensul in cazul arcului. De asemenea, la fel ca in cazul grafurilor orientate se defineste izomorfismul a doua grafuri neorientate.

Definitie: Daca oricare pereche [x, y] P (N) este imaginea a cel mult q, q > 1, elemente din A atunci G = ( N, A, g) se numeste multigraf neorientat.

Exemplu: Daca se elimina sageata de pe fiecare arc al grafului din Figura 1.1., atunci fiecare arc (x, y) devine o muchie [x, y] si graful devine

un multigraf neorientat cu q = 3.

In paragrafele si capitolele urmatoare ne vom ocupa de grafuri neorientate cu q = 1. In acest caz functia g este injectiva si familia A este o multime.Un graf neorientat cu q = 1 se numeste graf simplu si se noteaza G = ( N, A).

Definitie: Fie un arc a = (x, y) A. Nodurile x, y se numesc extremitatile arcului, nodul x este extremitate initiala si y extremitate finala; nodurile x si y se numesc adiacente.

Evident ca, pentru o muchie a = [x, y] A, nu se pot preciza extremitatea initiala si extremitatea finala.

Definitie: Fie un arc a = (x, y) A. Nodul x se numeste predecesor al nodului y si nodul y se numeste successor al nodului x. Multimea succesorilor nodului x este multimea V (x) = si multimea predecesorilor nodului x este multimea V (x) = . Multimea V(x) = V (x) U V (x) se numeste vecinatatea nodului x. Daca V(x) = Ø , atunci x se numeste nod izolat.

Exemplu: In graful din figura 1.1., pentru nodul 4 avem : V (4) = , V (4) = , V(4) = .

Definitie: Se spune ca nodul x este adiacent cu submultimea N Ì N, daca xÏ N si x V(N ), V(N U

Definitie: Doua arce se numesc adiacente daca au cel putin o extremitate in comun.

Definitie: Fie arcul a = ( x, y) A. Se spune ca arcul a este incident catre exterior la nodul x si incident catre interior la nodul y. Multimea arcelor incidente catre exterior la nodul x este E (x) = , multimea arcelor incidente catre interior la nodul x este E (x) = si multimea arcelor incidente la nodul x este E(x)= E (x) U E (x).

Numarul (x) = | E (x) | se numeste semigradul exterior al nodului x, numarul (x) = | E (x) se numeste semigradul interior al nodului x si numarul (x) = (x) + (x) se numeste gradul nodului x.

Exemplu: Se considera multigraful orientat din figura 1.1. Avem

(3) = 1, deci

Daca G = ( N, A, g) este un graf neorintat atunci (x) = . In cazul in care G = ( N, A, g) este multigraf orientat atunci ≥

| V (x) | , ≥ | V (x) | si in care G = ( N, A) este un digraf relatiile sunt verificate cu egalitati. Evident ca daca x este un nod izolat atunci

(x) = 0. Un nod x cu (x) = 1 se numeste perdant. Daca toate nodurile lui G au acelasi grad atunci G se numeste graf - regulat . Un graf 0 - regulat se numeste graf nul si un graf 3 - regulat se numeste graf trivalent sau cubic.

Definitie: Intr-un graf orientat G = ( N, A, g) se numeste lant de la nodul x1 la nodul xk+1, o secventa L = (x , a , x , .., xk, ak, xk+1) , xi N, i = 1,.., k+1, ai A , i = 1, .., k, cu proprietatea ca fiecare arc ai este de forma (xi, xi+1) sau (xi+1, xi ). Daca ai = (xi, xi+1), atunci ai se numeste arc direct al lantului si daca ai = (xi+1, xi ) , atunci ai se numeste arc invers al lantului. Numarul de arce din secventa este, prin definitie, lungimea lantului L. Lantul L se numeste simplu daca fiecare arc ai din secventa este utilizat o singura data si se numeste elementar daca fiecare nod xi din secventa este utilizat o singura data. Daca xk+1 = x atunci lantul simplu L se numeste ciclu si se noteaza L

Un lant poate fi reprezentat ca si o secventa de arce L = (a ,..., ak) si in cazul cand G = (N, A) este digraf ca o secventa de noduri L = (x ,..,xk+1

Exemplu: Se considera graful orientat din figura 1.1. Secventa L = (1, a , 2, a , 4, a , 2, a , 3, a , 2, a , 4) = (a , a , a , a , a , a ) este un lant, dar nu este nici lant simplu, nici lant elementar. Secventa L = (1, a , 2, a , 4, a , 2, a , 3, a , 2) = (a , a , a , a , a ) este un lant simplu, dar nu este elementar. Secventa L = (1, a , 2, a , 3, a , 5, a , 4) = (a , a , a , a ) este un lant elementar.

Notiunea de lant se poate defini si intr-un graf neorientat G = ( N, A, g) ca o secventa L = (x , a , x , .., xk, ak, xk+1) cu proprietatea ca fiecare muchie ai din secventa este de forma ai = [xi, xi+1] si lantul poate fi reprezentat si sub forma L = (a ,.., ak). Un lant L = (x , a , x , .., xk, ak, xk+1), al grafului orientat G = ( N, A, g), in care fiecare arc ai este arc direct, adica este de forma ai = (xi, xi+1), se numeste lant orientat sau drum si se noteaza prin D. Un lant simplu orientat cu xk+1 = x se numeste ciclu orientat sau circuit si se noteaza prin D Notiunile de drum si circuit au sens numai pentru grafuri orientate.

Exemplu: Se considera graful orientat din figura 1.1. Secventa D = (1, a , 2, a , 4, a , 2, a , 3, a , 2, a , 4, a , 2 ) = (a , a , a , a , a , a , a ) este un drum, dar nici drum simplu, nici drum elementar. Secventa D = (1, a , 2, a , 4, a , 2, a , 3, a , 5) = (a , a , a , a , a este un drum simplu, dar nu este un drum elementar. Secventa D = (3, a , 2, a , 4, a , 5) = (a , a , a ) este un drum elementar.

In paragrafele urmatoare vom considera, in general, lanturi si drumuri elementare, dar fara a mai specifica de fiecare data atributul "elementar", ci numai in cazurile cand este necesar.

Definitie: Se spune ca graful orientat G = ( N , A , g ) este un subgraf al grafului orientat G = ( N, A, g) daca N N si A A. Daca N N si A = (N N A atunci G = ( N , A , g ) se numeste subgraf indus in G de multimea de noduri N . Daca N = N si A A atunci G = ( N , A , g ) se numeste subgraf partial al lui G.

Concepte similare se pot defini in mod analog si pentru grafuri neorientate.

Fie G = ( N, A) un digraf cu multimea nodurilor N = si multimea arcelor A = . Matricea de adiacenta asociata digrafului G este matricea M = ( mi j n n , unde

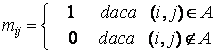
Evident ca au loc relatiile :

, iN, , , jN .

Matricea de incidenta asociata digrafului G este matricea = (i j n m unde

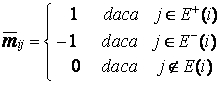
In acest caz au loc relatiile: