ELEMENTE DE GRAFURI. ALGORITMI.

Elemente de Grafuri. Algoritmi.

Definitie: Graf este o pereche ordonata de multimi G =(X, G), unde X este o multime de varfuri, iar G = XX este o multime de muchii sau arce (pentru grafuri orientate).

Exemplu:

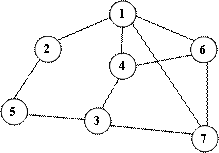
O muchie de la varful x la varful y este notata cu perechea ordonata (x, y), daca graful este orientat si in mod uzual este folosit termenul de arc, si cu multimea , daca graful este neorientat. In reprezentarea grafica, arcele (x,y) sunt marcate prin sageti de la extremitatea initiala x la cea finala y, iar muchiile prin segmente.

Intr-un graf orientat, existenta unui arc de la varful x la varful y nu presupune si existenta arcului de la y la x. In grafurile neorientate, daca exista muchie intre x si y, atunci aceasta este si muchie intre varfurile y si x. Varfurilor unui graf li se pot atasa informatii numite uneori valori, iar muchiilor li se pot atasa informatii numite costuri.

Urmatoarele notiuni sunt specifice grafurilor:

Doua varfuri unite printr-o muchie se numesc adiacente.

Un drum este o succesiune de muchii de forma:

(x₁, x₂), (x₂, x₃), , (x_n-1, x_n) - in graf neorientat

sau de forma

, , , - in graf neorientat

Un lant se defineste ca o succesiune de varfuri x₁, x₂, x₃, . x_n in care oricare doua varfuri sunt adiacente.

Intr-un drum simplu muchiile care il compun sunt distincte.

Intr-un drum elementar varfurile care il compun sunt distincte.

Lungimea drumului este egala cu numarul muchiilor care il constituie.

Un lant elementar al grafului G care contine toate varfurile grafului se numeste lant hamiltonian. Determinarea unui lant hamiltonian al grafului este o problema foarte populara cunoscuta ca Problema Comis Voiajorului rezolvata prin metoda Greedy.

Un ciclu este un drum care este simplu si care are drept capete un acelasi varf.

Un graf fara cicluri se numeste graf aciclic.

Un subgraf al lui G este un graf G'=(X', G ), unde X'  X, iar G este formata din muchiile din G care unesc varfuri din X'.

Un graf partial este un graf (X, G ), unde G  G

Un graf neorientat este conex, daca intre oricare doua varfuri exista un drum. Pentru grafuri orientate, aceasta notiune este intarita: un graf orientat este tare conex, daca intre oricare doua varfuri x si y exista un drum de la x la y si un drum de la y la x.

Reprezentarea grafurilor

1. Prin matricea de adiacenta A, in care A[i, j] = 1 daca varfurile i si j sunt adiacente, iar A[i, j] = 0 in caz contrar.
2. Prin liste de adiacenta: fiecare varf i are atasata lista de varfuri adiacente lui (pentru grafuri orientate, este necesar ca muchia sa plece din i).
3. Prin lista de muchii. Aceasta reprezentare este eficienta atunci cand se doreste examinarea tuturor muchiilor grafului.
4. Prin matricea costurilor (grafuri neorientate etichetate) C in care C[i, j] ≠0 este costul asociat muchiei, iar C[i, j] = 0     semnifica faptul ca nu exista muchie .

Parcurgerea grafurilor

Parcurgerea unui graf presupune vizitarea intr-o anumita ordine nodurilor grafului, o singura data fiecare. In functie de ordinea de parcurgere a varfurilor exista 2 metode de parcurgere:

1. Metoda parcurgerii in latime - Breadth First
2. Metoda parcurgerii in adancime - Depth First

1. Parcurgerea in latime Breadth First: se viziteaza varful stabilit initial x_s, apoi vecinii acestuia (varfurile adiacente) apoi vecinii vecinilor lui x_s, etc. Procedura de parcurgere in latime functioneaza dupa urmatorul principiu: atunci cand s-a ajuns intr-un varf oarecare x nevizitat, il marcam si vizitam apoi toate varfurile adiacente lui x ramase nevizitate, apoi toate varfurile nevizitate adiacente varfurilor adiacente lui x, etc. La parcurgerea in latime se foloseste o structura de coada pentru a putea vizita toti vecinii unui nod dat inainte de a-l marca drept vizitat.

Subalgoritm BreadthFirst (x) este //x reprezinta varful curent

C=Φ // initializare coada vida

*Marcheaza x ca vizitat

Inserare(C,x) //inserare varfului x in coada C

Cattimp (C≠Φ)

Scoate(C,y) //scoate din coada varful y

Pentru fiecare varf z, adiacent lui y

Daca z este nevizitat atunci

*Marcheaza z ca vizitat

Inserare(C,z)

SfDaca

SfPentru

SfCattimp

SfSubalgoritm

Observatie: marcarea unui varf ca fiind vizitat sau nevizitat se poate realiza prin folosirea unui tablou tab[1..n] ale carui elemente sunt asociate varfurilor grafului si au valori binare cu semnificatia: tab[i]=1 - varful i este vizitat, respectiv, tab[i]=0 - varful i este nevizitat

2. Parcurgerea in adancime presupune vizitarea varfului initial x_S si marcarea sa ca fiind vizitat, apoi se alege un varf x, adiacent lui x_S si se aplica aceiasi procedura - recursiv, avand ca punct de plecare varful x. Procedura de parcurgere in adancime a varfurilor unui graf se preteaza la o implementare recursiva. La terminarea procedurii curente (la revenirea din apelul recursiv), daca exista un alt varf adiacent varfului curent x, care nu a fost vizitat, apelam din nou procedura etc. Daca toate varfurile adiacente lui x au fost marcate ca vizitate se termina vizitarea varfului x.

Subalgoritm DepthFirst (x) este:

*Marcheaza x ca vizitat

Pentru fiecare varf y adiacent lui x

Daca y este nevizitat atunci

Cheama DepthFirst (y)

SfDaca

SfPentru

SfSubalgoritm

Observatie: Varianta nerecursiva a subalgoritmului DepthFirst se realizeaza prin utilizarea unei structuri de date de tip stiva.

Subalgoritmii BreadthFirst si DepthFirst sunt apelati din algoritmul Parcurgere:

Algoritm Parcurgere(G) este

Pentru fiecare x din X

*Marcheaza x ca nevizitat

SfPentru

Pentru fiecare x din X

Daca x este nevizitat atunci

Cheama BreadthFirst (x) sau Cheama DepthFirst (x)

SfDaca

SfPentru

SfAlgoritm

In cazul unui graf neconex, se pune problema determinarii componentelor sale conexe:

O componenta conexa a grafului G=(X, M), este un subgraf G'=(X', M'), conex si maximal. Maximalitatea se refera la faptul ca nu exista lant in graful G care sa aiba o extremitate in X' si pe cealalta in XX'.

Un arbore este un graf neorientat, aciclic si conex. Intr-un arbore exista exact un drum intre oricare doua varfuri.

Un graf partial care este arbore se numeste arbore partial. Un arbore partial este un graf partial fara cicluri.

Arborele partial de cost minim (suma costurilor muchiilor este minima) se determina printr-un algoritm de tip Greedy: Algoritmul lui Kruskal.

Algoritmul de determinare a Arborele partial de cost minim (APM)

Problema APM: Se da un graf G=(X,G) cu muchiile etichetate prin costuri (datele de intarre sunt reprezentate prin matricea costurilor).Se cere determinarea arborelui partial de cost minim a grafului dat. (datele de iesire sunt muchiile care formeaza arborele partial de cost minim)

Rezolvare: Algoritmul lui Kruskal este un algoritm cunoscut de rezolvare a problemei enuntate si este un algoritm de tip Greedy. Principiul acestui algoritm este urmatorul:

Considerand graful G=(X,G), A=(X, G') - arborele ce se determina (reprezentat prin lista de muchii) si n - numarul de varfuri n=|X|:

se porneste cu arborele vid: G

in mod repetat se alege muchia de cost minim a grafului G care nu formeaza ciclu in arborele A si se adauga la G

algoritmul se termina cand au fost alese n-1 muchii

Algoritm Kruskal este:

Date de intrare: G=(X,G

Fie G

Cattimp (|G'|<n-1)

*Alege de cost minim din G

Daca G' nu contine cicluri

G G'

G G

SfDaca

SfCattimp

Date de iesire: A=(X,G

SfAlgoritm

Observatie: Multimea muchiilor grafului dat se poate ordona descrescator dupa costuri si se va parcurge in mod secvential, fara a mai fi necesara procedura de alegere a muchiei de cost minim din graful G.