| CATEGORII DOCUMENTE |
O functie este numita functie recursiva daca ea se autoapeleaza, fie direct (in definitia ei se face apel la ea insasi), fie indirect (prin apelul altor functii).
In cadrul acestui capitol vom aborda ambele tipuri de recursivitate:
■ recursivitate directa
■ recursivitate indirecta.
Va reamintim cateva observatii fundamentale de care e bine sa tineti cont:
a) Studiati felul in care apare recursivitatea intr-un program si daca sunt si alte moduri de elaborare a programului. Daca sunt, atunci verificati daca scrierea lor este mai eficienta si daca in cele din urma optati pentru recursivitate.
b) Puneti in evidenta modul in care o problema se apeleaza pe ea insasi.
c) Fiti atenti la modul in care definiti parametrii functiilor recursive, variabilele interne si globale. Unele definitii sunt fundamentale pentru executia programului. Spre exemplu variabilele folosite pentru a parcurge valorile permise ale componentelor unei solutii trebuie sa fie locale functiei, altfel nu se genereaza corect solutia. Unele definitii bine alese pot optimiza destul de mult spatiul alocat pe stiva si timpul de executie.
d) Pentru corectitudinea recursivitatii realizate fiti atenti la modul in care se pastreaza valorile datelor la iesirea dintr-un apel recursiv. Aveti grija ca dupa iesirea din apelul recursiv al unei functii sa refaceti datele modificate pentru noul apel.
e) Aveti grija la stocarea datelor intermediare. Daca este necesara o determinare a unui optim, se va lucra cu doua seturi de date: unul pentru stocarea optimului si unul pentru generarea solutiei curente. in acest caz tiparirea solutiei nu se face in interiorul recursivitatii, ci dupa terminarea tuturor apelurilor.
f) Aveti grija sa puneti corect conditiile de iesire din recursivitate. Fara acestea un program nu se va opri niciodata.
g) Faceti pregatirile necesare si stabiliti valorile parametrilor pentru primul apel.
Atragem atentia ca orice nerespectare a uneia dintre observatiile enumerate mai sus poate determina erori.
Pn = n! ; Anm = ; Cnm =
//Analiza combinatorica
#include<stdio.h>
int fact (int n)
void main()
Sa se calculeze matricea A(LxL), L 10 unde:
ACK2(i,j), daca i>j,
a(i,j)= 1, daca i=j,
sqrt(ACK(j,i)), daca i<j,
unde functia ACK(m,n) este o functie recursiva Ackerman definita pentru m 0 si n 0 prin:
ACK(0,n) = n+1;
ACK(m,0) = ACK(m-1,1);
ACK(m,n) = ACK(m-1, ACK(m,n-1);
//Functii recursive - Ackerman
#include<conio.h>
#include<stdio.h>
#include<math.h>
#define DIM 4
double ack(int m, int n);//prototipul
void scrie(double mat[DIM][DIM]);//prototipul
void main()
//Definirea functiilor
double ack(int m, int n)
void scrie(double mat[DIM][DIM])
Sa se se scrie un program care citeste doi intregi pozitivi m si n, de tip long, calculeaza si afiseaza pe cel mai mare divizor comun al lor. Programul va folosi o functie care are ca parametri doi intregi m si n de tip long si care calculeaza si returneaza cel mai mare divizor comun al lor.
Notam cu: (m,n) cel mai mare divizor comun al numerelor m si n. Calculul celui mai mare divizor comun a doua numere se poate realiza recursiv astfel:
(m,n) = m daca n = 0;
(m,n) = n daca m = 0;
(m,n) = (n,m%n) daca atit m, cat si n sunt diferiti de zero si m > n (prin m%n s-a notat restul impartirii lui m la n).
#include <stdio.h>
#include <stdlib.h>
//FUNCTIA
long cmmdc(long m, long n) /* calculeaza si returneaza pe cel mai mare divizor comun al numerelor m si n */
void main() /* citeste pe m si n de tip long, calculeaza si afiseaza (m,n) */
printf('m=%ldtn=%ldt(m,n)=%ldn',m,n,cmmdc(m,n));
in prima varianta vom defini functia recursiva permutare. Aceasta va genera permutarile verificand la fiecare pozitie daca elementul curent a fost deja selectat i nu. Daca nu este selectat, el poate fi folosit pentru aceasta pozitie. Iesirea din recursivitate se va face in momentul cand s-au generat toate cele n componente.
#include<stdio.h>
int k,n,poz[20],p[20];
void permutare(int i);
void main ()
void permutare(int i)
else permutare(i+1);
poz[j]=0; /* deselectam elementul j */
}
Varianta a doua va defini functia recursiva permuta de generare a permutarilor, care face generarea tuturor permutarilor prin interschimbarea elementului de pe pozitia curenta k, pe rand cu elementele din pozitiile anterioare, de la 1 la k-1. Cand se ajunge la prima pozitie se tipareste permutarea generata.
//Generarea tuturor permutarilor unei multimi.
#include <stdio.h>
int a[100] ;
int n, k, i ;
void tipareste(int n)
void permuta(int k)
}
void main()
Sa se afiseze toate posibilitatile de aranjare a n regine pe o tabla de sah de dimensiuni n x n astfel incat ele sa nu se atace.
Pentru a simplifica determinarea configuratiilor corecte vom folosi pentru fiecare linie o regina. Coloanele pentru fiecare regina se vor stoca in vectorul r. Generarea reginelor se face cu ajutorul functiei recursive regina care va avea ca parametru numarul liniei.
Pentru a accepta pozitia curenta se verifica daca regina asezata acum se ataca pe coloana sau pe diagonala cu reginele plasate anterior.
Pentru aceasta vom defini functia ataca pentru a verifica daca la adaugarea reginei de pe linia i aceasta se ataca cu una din reginele 1, 2,, i-1. Ea va returna valoarea 0, daca regina i nu ataca nici o regina si valoarea 1 in caz contrar. Doua regine se ataca daca sunt pe aceeasi coloana sau pe aceeasi diagonala. A doua conditie revine la a verifica daca diferenta dintre liniile pe care sunt situate reginele este egala cu diferenta dintre coloanele acestora, in valoare absoluta.
Pentru afisarea unei table de sah si a configuratiei reginelor am folosit functia scrie. Pentru numararea solutiilor generate am folosit variabila nr.
//Problema reginelor
#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
int r[20],n,nr;
int ataca(int);
void regina(int);
void scrie(void);
void main()
void regina(int i)
int ataca(int i)
void scrie()
cprintf('nr');
}
printf('Ptr continuare apasati orice tasta!');
getch();
O persoana are un rucsac cu care poate transporta o greutate maxima G. Persoana are la dispozitie n obiecte diferite si cunoaste pentru fiecare obiect greutatea si castigul care se obtine in urma transportului sau la destinatie. Se cere sa se precizeze care obiecte trebuie sa le transporte persoana astfel incat castigul sa fie maxim.
Varianta recursiva a problemei va utiliza functia rucsac. Aceasta va calcula pentru fiecare obiect daca selectia sa duce la depasirea greutatii maxime admisibile. Daca nu, se verifica daca actuala configuratie are o valoare maxima. In caz afirmativ se stocheaza obiectele care dau pentru selectie o valoare maxima. Tiparirea obiectelor care au impreuna valoarea maxima se va face la iesirea din recursivitate.
//Problema rucsacului
#include<stdio.h>
#include<stdlib.h>
#include<conio.h>
#define DIM
float gx,vx,gmax,vmax,g[DIM],v[DIM];
int s[DIM],smax[DIM],n;
void rucsac(int i) //i - nr curent max de obiecte
for(k=i+1;k<=n;k++)
}
/*Apelul recursiv pentru trecerea la urmatorul obiect*/
if(i<n) rucsac(i+1);
/*Refacerea starii dupa iesirea din recursivitate*/
gx-=j*g[i] ; vx-=j*v[i] ;
}
void main()
Observati modul in care s-a modificat programul atunci cand se cere o configuratie de optim:
in interiorul functiei recursive se face doar verificarea de optim si stocarea in cazul indeplinirii conditiilor de optim a datelor intermediare intr-un set de date separat.
tiparirea solutiei s-a facut la iesirea din apelul recursiv si nu in interior.
Fiind date n tipuri de prajituri cu costul c[1], c[2], , c[n], sa se determine toate modurile posibile de a cumpara m prajituri care sa nu depaseasca suma s. Se considera ca pot fi cumparate oricate prajituri de un anumit tip.
Notatii facute:
x, stocheaza cate prajituri s-au cumparat din fiecare tip;
suma, valoarea prajiturilor cumparate in momentul de fata;
nr, numarul de prajituri cumparate in momentul de fata.
in procedura recursiva rec numarul maxim de prajituri care se pot cumpara este minimul dintre numarul de prajituri ramase de cumparat, m, si numarul posibil de cumparat cu suma ramasa din prajiturile de tipul i, adica (s-suma)/c[i]. Datele se citesc din fisierul 'prajitur.in' iar solutiile se scriu in fisierul 'prajitur.out'. Programul a fost realizat in C++:
//Prajituri
#include<iostream.h>
#include<fstream.h>
long x[100] ,c[100];
short k,i,j,n,m,nr;
unsigned nr_sol;
unsigned long s,suma;
fstream f;
void rec(int i)
nr-=j;
suma-=c[i]*j;
}
void main()
Se stie ca din numarul 4 se obtine orice numar natural n scris in baza zece prin aplicarea urmatoarelor operatii:
Se cere sa se scrie un program care produce un sir de numere conform regulilor precedente in care primul numar este 4 iar ultimul este n.
Se pleaca de la numarul n si se genereaza operatiile inverse celor mentionate. Programul este format din 2 functii intre care se face recursivitatea indirecta:
proc2 -se inmulteste numarul cu 2. Daca ultima cifra este 0 sau 4 se apeleaza proc0, altfel se apeleaza proc2.
proc0 -se sterge ultima cifra daca este 0 sau 4. Apelul recursiv este asemanator cu proc0: daca ultima cifra este 0 sau 4 se apeleaza proc0, altfel se apeleaza proc2.
#include<conio.h>
#include<stdio.h>
int n,a[100]; /*numarul initial si sirul de transformari*/
void proc2(int k);/*proceduri de transformare*/
void procO(int k);
void proc2(int k) /* se inmulteste numarul cu 2 */
void procO(int k) /* se elimina ultima cifra */
void main(void)
printf('Sirul de numere este: ');
for(p=a[0];p>=1;p--) printf(' %d ',a[p]);
getch();
Asemanari intre transferul parametrilor unei functii prin pointeri si prin referinta.
Caracteristicile modului de transfer a parametrilor unei functii prin pointeri.
Caracteristicile variabilelor globale.
Caracteristicile variabilelor locale.
Care este diferenta intre antetul unei functii si prototipul acesteia ?
Care sunt modurile de alocare a memoriei ?
Care sunt modurile de transfer a parametrilor unei functii ?
Care sunt operatorii din C++ care permit alocarea/dezalocarea dinamica a memoriei ?
Ce clase de memorare cunoasteti ?
Ce este domeniul de vizibilitate a unei variabile ?
Ce este prototipul unei functii ?
Ce este timpul de viata a unei variabile ?
Ce loc ocupa declaratiile variabilelor locale in corpul unei functii ?
Ce reprezinta antetul unei functii ?
Ce rol are declararea functiilor ?
Ce se indica in specificatorul de format al functiei printf ?
Ce sunt functiile cu numar variabil de parametri ? Exemple.
Ce sunt functiile cu parametri impliciti ?
Ce sunt pointerii catre functii ?
Ce sunt variabilele referinta ?
Cine determina timpul de viata si domeniul de vizibilitate ale unei variabile ?
Comparatie intre declararea si definirea functiilor.
Diferente intre modurile de transfer a parametrilor prin valoare si prin referinta.
Diferente intre modurile de transfer a parametrilor unei functii prin pointeri si prin referinta.
Din apelul functiei printf se poate omite specificatorul de format ?
Din ce este formata o functie ?
In ce zona de memorie se rezerva spatiu pentru variabilele globale ?
O functie poate fi declarata in corpul altei functii ?
O functie poate fi definita in corpul unei alte functii ?
Parametrii formali ai unei functii sunt variabile locale sau globale ?
Transferul parametrilor prin valoare.
Ce rol au parametrii formali ai unei functii ?
Sa se scrie un program care citeste cate doua numere, pana la intalnirea perechii de numere 0, 0 si afiseaza, de fiecare data, cel mai mare divizor comun al acestora, folosind o functie care il calculeaza.
Se introduce de la tastatura un numar intreg. Sa se afiseze toti divizorii numarului introdus. Se va folosi o functie de calcul a celui mai mare divizor comun a 2 numere.
Secventele urmatoare sunt corecte din punct de vedere sintactic ? Daca nu, identificati sursele erorilor.
q void a(int x, y)
void main( )
q void main( )
int f(int z)
Scrieti o functie gaseste_cifra care returneaza valoarea cifrei aflate pe pozitia k in cadrul numarului n, incepand de la dreapta (n si k vor fi argumentele functiei).
Implementati propriile versiuni ale functiile de lucru cu siruri de caractere (din paragraful 4.4).
Sa se calculeze valoarea functiei g, cu o eroare EPS (a, b, EPS citite de la tastatura):
g(x)=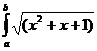
*ln|x+a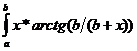|dx + 
dx
Implementati functii iterative si recursive pentru calculul valorilor polinoamelor Hermite Hn(y), stiind ca: H0(y)=1, H1(y)=2y, Hn(x)=2yHn-1(y)-2Hn-2(y) daca n>1. Comparati timpul de executie al celor doua functii.
Sa se scrie un program care genereaza toate numerele palindrom, mai mici decat o valoare data, LIM. Un numar palindrom are cifrele simetrice egale (prima cu ultima, a doua cu penultima, etc). Se va folosi o functie care testeaza daca un numar este palindrom.
Fie matricea C (NXN), N<=10, ale carei elemente sunt date de relatia:
, unde xI ,
x introdus de la tastatura
j! +
, daca i<j
Ci,j = xi, daca i=j
i!
+ 
, daca i>j
a) Sa se implementeze urmatoarele functii: de calcul a elementelor matricii; de afisare a matricii; de calcul si de afisare a procentului elementelor negative de pe coloanele impare (de indice 1, 3, etc).
b) Sa se calculeze si sa se afiseze matricea B, unde: B = C - C2 + C3 - C4 + C5.
Sa se creeze o biblioteca de functii pentru lucrul cu matrici, care sa contina functiile utilizate frecvent (citirea elementelor, afisarea matricii, adunare a doua matrici, etc). Sa se foloseasca aceasta biblioteca.
Sa se creeze o biblioteca de functii pentru lucrul cu vectori, care sa contina functiile utilizate frecvent. Sa se foloseasca aceasta biblioteca.
|
Politica de confidentialitate | Termeni si conditii de utilizare |
Vizualizari: 4154
Importanta: 
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved
