| CATEGORII DOCUMENTE |
DOCUMENTE SIMILARE |
|
TERMENI importanti pentru acest document |
|
| : | |
Se dau m vectori sortati crescator, v(i)=(v(i,1), , v(i, n(i)), i=1, , m si se cere algoritmul de interclasare a acestora cu numar minim de comparatii.
Rezolvare. Daca interclasarea a doi vectori v(1), v(2) o facem prin algoritmul prezentat anterior, atunci numarul de comparatii este cel mult n(1)+n(2). In functie de ordinea de interclasare a vectorilor se obtine un numar diferit de comparatii. Deci trebuie sa gasim o ordine care conduce la un numar minim de comparatii.
Exemplul 5.5
Vom nota cu v(i)![]() v(j) vectorul obtinut prin interclasarea lui v(i) cu
v(j). Daca avem v(1)=(2, 4, 6, 8), v(2)=(1, 2, 3) si v(3)=(1, 3, 5,
7, 9, 11) atunci:
v(j) vectorul obtinut prin interclasarea lui v(i) cu
v(j). Daca avem v(1)=(2, 4, 6, 8), v(2)=(1, 2, 3) si v(3)=(1, 3, 5,
7, 9, 11) atunci:
Din acest exemplu se observa ca este bine ca vectorii cu dimensiuni mici sa se interclaseze mai intai si apoi vectorii cu dimensiuni mari. Strategia Greedy va fi ca la fiecare pas sa selectam doi vectori de dimensiune minima.
La fiecare iteratie pastram in matricea v vectorii v(i) descrescator dupa n(i). Se selecteaza ultimii doi vectori din matricea v. Dupa realizarea interclasarii noul vector se insereaza in matricea v folosind, de exemplu, insertia directa.. Procedeul se repeta pana sunt interclasati toti vectorii.
(1)PROGRAM INTEROPT;
(2)BEGIN
READ M, (N(i),i:=1 TO M), ((V(I,J),I:=1 TO M),J:=1 TO N(I));
SORT(M, N, V);
FOR I:= M DOWNTO 2 DO
INTER(N(I-1), V(I-1), N(I), V(I), W);
J:=I-2;
WHILE (J>0) AND (N(J)<N(I-1)+N(I)) DO
FOR K:=1 TO N(J) DO
V(J+1,K):=V(J,K);
ENDFOR;
N(J+1):=N(J); J:=J-1;
ENDWHILE;
FOR K:=1 TO N(I-1)+N(I) DO
V(J+1,K):=W(K);
ENDFOR;
N(J+1):=N(I-1)+N(I);
(18) ENDFOR;
(19) WRITE V(1,J), 1 ≤ J ≤ N(1);
(20)END.
Procedura SORT face sortarea liniilor matricei v descrescator in functie de vectorul n si procedura INTER face interclasarea directa a doi vectori.
Pentru a analiza corectitudinea algoritmului definim printr-o formula recursiva arborele asociat unei strategii de interclasare.
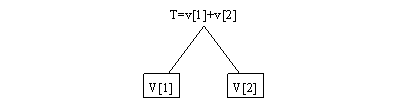
Fig. 5.7
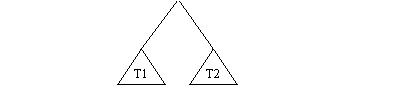
Fig. 5.8
Arborele asociat unui sir de vectori verifica urmatoarele afirmatii:
![]() , unde d[i] este nivelul in T al vectorului v[i].
, unde d[i] este nivelul in T al vectorului v[i].
Teorema 5.4
Algoritmul InterOpt determina interclasarea vectorilor v[i], i=1,n cu numar minim de comparatii realizate in interclasarile directe.
Demonstratie
Se observa ca arborele asociat unei strategii de interclasare
este arborele Huffman asociat numerelor nr[1], nr[2], , nr[n]. Algoritmul anterior repeta modul de
constructie al arborelui Huffman deci suma ![]() este minima
si implicit L(T) este minim. Rezulta o strategie de interclasare
optima.
este minima
si implicit L(T) este minim. Rezulta o strategie de interclasare
optima.
Teorema 5.5
Daca L este numarul de comparatii rezultat din interclasarile directe atunci algoritmul InterOpt are complexitate O(L+n2).
Demonstratie
Complexitatea algoritmului este data de numarul de
comparatii facut de interclasarile directe si de
numarul de comparatii dat de pastrarea structurii v. In primul
caz numarul este n. Pentru cel de-al doilea caz se observa ca
inserarea directa foloseste cel mult i-1 comparatii pentru
punerea sirului y in structura v. Gasim in total un numar de ![]() comparatii.
comparatii.
Daca se utilizeaza o inserare binara in structura v atunci complexitatea algoritmului devine O(L+nlogn).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3758
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved