METODE DE ELABORARE A ALGORITMILOR.GREEDY

Metode de elaborare a algoritmilor.Greedy

Metoda Greedy (greedy = (en.)lacom) este o tehnica de rezolvare problemelor de optimizare bazata pe principiul alegerii "lacome" a optimului local in vederea determinarii optimului global. Solutia unei probleme abordata cu metoda Greedy se construieste treptat, prin alegeri corecte, optimale si irevocabile ale solutiilor partiale. Dezavantajul major al metodei consta in incapacitatea determinarii solutiei optime globale pentru orice problema.

Pentru a aplica metoda Greedy, problema abordata trebuie reformulata intr-o maniera sablon prin care se pot identifica datele de intrare sub forma unei multimi A, datele de iesire sub forma unei submultimi B a multimii de intrare A si anumite conditii specifice problemei care ne permit alegerea unei solutii partiale optimale:

Fie A o multime de n elemente: A=.

Se cere determinarea submultimii B, astfel incat B este maximala si verifica anumite conditii.

Principiul de rezolvare:

Se porneste cu multimea vida B=, care ulterior va fi completata cu elemente ale multimii A

Se parcurge multimea A, element cu element, si se verifica pentru fiecare membru al multimii A conditiile identificate din contextul problemei. Daca aceste conditii sunt verificate, elementul respectiv va fi "inghitit" de multimea B

Procedeul se incheie in doua situatii:

o        S-a determinat multimea maximala B

o        Nu mai sunt elemente de parcurs in multimea A

Exista doua variante ale algoritmului Greedy:

cu ordonarea in prealabil a multimii A

fara ordonarea multimii A

Descrierea algoritmica a metodei generale este prezentata in continuare, cu mentiunea ca propozitiile nestandard (introduse prin prefixarea cu simbolul*) nu pot fi rafinate decat pentru problema concreta de rezolvat:

Algoritm Greedy este: //varianta fara ordonarea multimii A

Date de intrare: A

Date de iesire: B

Fie B=

Cattimp (A≠Φ) si (*B nu este optima)

*Alege a_i din A

Daca B *este solutie posibila atunci

B = B sau * a_i inlocuieste un element din B

A=A

SfDaca

SfCattimp

SfAlgoritm

Algoritm Greedy2 este: //varianta cu ordonarea multimii A dupa un criteriu

Date de intrare: A

Date de iesire: B

Fie B=

*Ordoneaza multimea A

Pentru i de la 1 la n

Daca B este solutie posibila atunci

B = B sau a_i inlocuieste un element din B

SfDaca

SfPentru

SfAlgoritm

Problema 1. Problema monedelor.

Se considera o multime infinita de monede de valori 1,k¹,k²,,k^n-1 si S o suma exprimabila prin aceste monede. Se cere determinarea unei scheme de exprimare a sumei S utilizand un numar optim (minim) de monede.

Analiza problemei:

Din problema formulata mai sus putem deduce multimea de intrare A ca fiind multimea monedelor de valori 1,k¹,k²,,k^n-1, considerand ca numarul de monede de aceiasi valoare este nelimitat. Solutia problemei este reprezentata dintr-o submultime B de monede, nu neaparat de valori diferite, astfel incat dimensiunea submultimii este minima si suma valorilor monedelor continute de B nu depaseste suma data S.

Rezolvarea logica a problemei consta in parcurgerea pasilor:

initializeaza multimea B cu multimea vida

se alege cea mai mare unitate monetara k^j care este mai mica valoric decat suma S

Cat timp suma S ramane pozitiva adauga moneda k^j la multimea B si scade valoarea monedei din suma S

alege monede de valoare imediat mai mica decat k^j, respectiv, k^j-1

Cat timp suma S ramane pozitiva adauga moneda k^j-1 la multimea B si scade valoarea monedei k^j-1din suma S

alege monede de valoare imediat mai mica decat k^j-1, respectiv, k^j-2

Procesul se continua pana cand nu mai exista valori monetare mai mici care ar putea fi adaugate multimii B

Procedeul descris anterior corespunde unui algoritm Greedy: solutia globala se construieste treptat prin alegeri succesive si irevocabile ale unitatilor monetare ce intra in alcatuirea schemei de exprimare a sumei S. Lacomia procedeului este data de maniera de parcurgere a valorilor monetare, de la cele mai mari inspre cele mai mici, ceea ce permite formarea unei multimi B de dimensiune minima (cu cat valorile monetare sunt mai mari, cu atat numarul monedelor prin care se exprima S este mai mic).

Algoritmul GreedyUnitatiMonetare este:

Date de intrare: S,k,n

Date de iesire: B

Fie B=

*Cauta cel mai mare j pentru care k^j<=S

Cattimp (j≥0)

Cattimp (S- k^j ≥ 0)

S=S- k^j

B=B

SfCattimp

j=j-1 //alege urmatoarea valoare monetara, mai mica

SfCattimp

Datele de intrare ale algoritmului descris sunt suficiente pentru a defini multimea A: cunoscand k, n si faptul ca numarul de monede de acelasi tip este nelimitat, multimea A se subintelege ca fiind: A=

Problema 2. Problema Rucsacului. Se considera o multime A de n obiecte caracterizate fiecare prin capacitate si importanta: A= :

, w_i - importanta obiectului a_i

, c_i - importanta obiectului a_i

Se cere determinarea unei scheme de incarcare optima a unui rucsac de capacitate maxim permisa C cu obiecte din multimea A: suma importantelor obiectelor selectate trebuie sa fie maxima si suma capacitatilor obiectelor selectate nu trebuie sa depaseasca capacitatea maxima C.

Observatie: Varianta fractionara a problemei rucsacului permite ca anumite obiecte sa fie incarcate in fractiuni, solutia finala oferita de metoda Greedy fiind optimul global. Pentru problema discreta a rucsacului (obiectele nu pot fi impartite pe fractiuni), metoda Greedy nu determina intotdeauna optimul global.

Analiza problemei (varianta discreta): Strategia de incarcare a rucsacului (initial gol) este de a introduce treptat in rucsac acel obiect din multimea obiectelor disponibile, pentru care raportul capacitate - importanta este minim, ceea ce corespunde construirii unei solutii partiale optime. Practic, la fiecare pas de construire a solutiei vom prefera un obiect de importanta mare si capacitate mica. Alegerea "lacoma" a obiectelor garanteaza obtinerea unei solutii finale bune. Faptul ca asupra alegerilor efectuate nu se revine determina ca in multe situatii solutia optima globala sa nu poata fi gasita.

Se observa ca multimea obiectelor A se parcurge in ordine crescatoare dupa raportul capacitate - importanta, ceea ce ne conduce la construirea unui algoritm Greedy in varianta a doua, cu ordonarea elementelor multimii A.

Algoritmul de rezolvare a problemei rucsacului, varianta discreta, este descris in continuare:

Algoritm Rucsac este:

Date de intrare: A=

//pentru care se cunosc w_i si c_i ,

Date de intrare: C -capacitatea rucsacului

Date de iesire B //multimea obiectelor selectate in rucsac

Ordoneaza A , crescator dupa valorile rapoartelor w_i/c_i

Fie C_B=0 //suma capacitatilor obiectelor selectate

Fie B=

Pentru i de la 1 la n

Daca ( C_B + c_i ≤ C ) atunci

B=B

C_B =C_B + c_i

SfDaca

SfPentru

SfAlgoritm

Problema 3. Planificarea spectacolelor. Se considera o multime de n activitati (spectacole) A= , fiecare activitate a_i fiind caracterizata prin ora de debut s_i si ora de terminare t_i. Intr-o sala de spectacole, se doreste o selectie a activitatilor disponibile astfel incat sa fie derulate, intr-o singura zi cat mai multe spectacole si acestea sa nu se intercaleze.

Se cere un orar al spectacolelor astfel incat numarul lor sa fie maxim posibil si sa nu existe suprapuneri.

Analiza problemei: Din analiza specificatiilor problemei se deduce imediat formularea specifica unei probleme rezolvabile prin metoda Greedy:

Se da A=

Se cere astfel incat B este maximala si verifica anumite conditii. Conditiile se refera la ne-suprapunerea oricaror doua activitati planificate.

Ceea ce este dificil de stabilit, este maniera de alegere, la fiecare pas, a urmatoarei activitati din multimea activitatilor disponibile (neplanificate deja), pentru a obtine in final o planificare optima.

Identificam trei variante de alegere a urmatoarei activitati pe care o planificam :

in ordine crescatoare, dupa timpul de start s_i

in ordine crescatoare, dupa durata activitatii: d_i = ti-s_i

in ordine crescatoare, dupa timpul de terminare t_i

Dintre cele trei variante enuntate, doar cea de-a treia se dovedeste plauzibila. Pentru primele doua cazuri vom demonstra ineficienta prin contraexemple:

Contraexemplu 1.

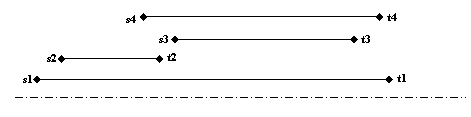
Consideram cazul particular descris in imaginea alaturata. Fiecare activitate este reprezentata printr-un segment ale carui capete marcheaza timpul de start si de terminare. Prin alegerea spectacolelor in ordinea crescatoare a timpului de debut, se va alege ca prima activitate planificata: a₁ si se constata imposibilitatea selectarii unei alte activitati fara sa existe suprapuneri. Algoritmul ar furniza in acest caz solutia B= cu toate ca exista o solutie mai buna: B=.

Contraexemplu 2.

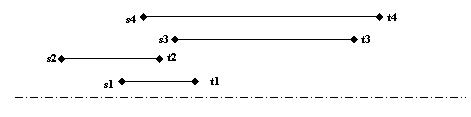
Prin alegerea in ordinea crescatoare a duratei activitatilor disponibile, in cazul particular figurat in imaginea alaturata, prima activitate selectata este a₁. Aceasta alegere se dovedeste neinspirata deoarece nicio alta activitate nu va mai putea fi planificata ulterior, datorita suprapunerilor. Solutia ar fi in acest caz B= cu toate ca exista o solutie mai buna: B=.

Algoritmul de rezolvare a problemei planificarii spectacolelor implica ordonarea multimii de intrare, crescator, dupa timpul de terminare a activitatilor:

Algoritm GreedySpectacole este:

Date de intrare: A= // pentru care se cunosc s_i si t_i ,

Date de iesire B

Fie B=

*Ordoneaza crescator A dupa valorile t_i

Pentru i de la 1 la n

Daca *(nu exista a_j B, astfel incat a_i se suprapune lui a_j) atunci

B=B

SfDaca

SfPentru

SfAlgoritm

Observatie: Doua activitati a_i si a_j se considera ca nu se suprapun ddaca este verificata conditia:s_i>t_j sau s_j>t_i.