| CATEGORII DOCUMENTE |
STRUCTURI DE DATE EXTERNE
1 Specificul datelor pe suport extern
Principala diferenta dintre memoria interna (RAM) si memoria externa (disc) este modul si timpul de acces la date:
- Pentru acces la disc timpul este mult mai mare decat timpul de acces la RAM (cu cateva ordine de marime), dar printr-un singur acces se poate citi un numar mare de octeti (un multiplu al dimensiunii unui sector sau bloc disc);
- Datele memorate pe disc nu pot folosi pointeri, dar pot folosi adrese relative in fisier (numere intregi lungi). Totusi, nu se folosesc date dispersate intr-un fisier din cauza timpului foarte mare de repozitionare pe diferite sectoare din fisier.
In consecinta apar urmatoarele recomandari:
- Utilizarea de zone tampon ("buffer") mari, care sa corespunda unui numar oarecare de sectoare disc, pentru reducerea numarului de operatii cu discul (citire sau scriere);
- Gruparea fizica pe disc a datelor intre care exista legaturi logice si care vor fi prelucrate foarte probabil impreuna; vom numi aceste grupari "blocuri" de date ("cluster" sau "bucket").
- Amanarea modificarilor de articole, prin marcarea articolelor ca sterse si rescrierea periodica a intregului fisier (in loc de a sterge fizic fiecare articol) si colectarea articolelor care trebuie inserate, in loc de a insera imediat si individual fiecare articol.
Un exemplu de adaptare la specificul memoriei externe este chiar modul in care un fisier este creat sau extins pe mai multe sectoare neadiacente. In principiu se foloseste ideea listelor inlantuite, care cresc prin alocarea si adaugarea de noi elemente la lista. Practic, nu se folosesc pointeri pentru legarea sectoarelor disc neadiacente dar care fac parte din acelasi fisier; fiecare nume de fisier are asociata o lista de sectoare disc care apartin fisierului respectiv (ca un vector de pointeri catre aceste sectoare). Detaliile sunt mai complicate si depind de sistemul de operare.
Un alt exemplu de adaptare la specificul memoriei externe il constituie structurile arborescente: daca un sector disc ar contine mai multe noduri oarecare dintr-un arbore binar, atunci ar fi necesar un numar mare de sectoare citite (si recitite) pentru a parcurge un arbore. Pentru exemplificare sa consideram un arbore binar de cautare cu 4 noduri pe sector, in care ordinea de adaugare a cheilor a condus la urmatorul continut al sectoarelor disc (numerotate 1,2,3,4) :
50, 30, 40, 20 70, 80, 35, 85 60, 55, 35, 25 65, 75, -, -
Pentru cautarea valorii 68 in acest arbore ar fi necesara citirea urmatoarelor sectoare, in aceasta ordine:
1 (radacina 50), 2 (compara cu 70), 3 (compara cu 60), 4 (compara cu 65)
Solutia gasita a fost o structura arborescenta mai potrivita pentru discuri, in care un sector (sau mai multe) contine un nod de arbore, iar arborele nu este binar pentru a reduce numarul de noduri si inaltimea arborelui; acesti arbori se numesc arbori B.
Structurile de date din memoria RAM care folosesc pointeri vor fi
salvate pe disc sub o alta forma, fara pointeri; operatia se numeste si
"serializare". Serializarea datelor dintr-un arbore, de exemplu, se va face prin traversarea arborelui de la radacina catre
Serializarea datelor dintr-o foaie de calcul ("spreadsheet") se va face scriind pe disc coordonatele (linie,coloana) si continutul celulelor, desi in memorie foaia de calcul se reprezinta ca o matrice de pointeri catre continutul celulelor.
De multe ori datele memorate permanent pe suport extern au un volum foarte mare ceea ce face imposibila memorarea lor simultana in memoria RAM. Acest fapt are consecinte asupra algoritmilor de sortare externa si asupra modalitatilor de cautare rapida in date pe suport extern.
Sistemele de operare moderne (MS-Windows si Linux) folosesc o memorie virtuala, mai mare decat memoria fizica RAM, dar totusi limitata. Memoria virtuala inseamna extinderea automata a memoriei RAM pe disc (un fisier sau o partitie de "swap"), dar timpul de acces la memoria extinsa este mult mai mare decat timpul de acces la memoria fizica si poate conduce la degradarea performantelor unor aplicatii cu structuri de date voluminoase, aparent pastrate in memoria RAM.
2 Sortare externa
Sortarea externa, adica sortarea unor fisiere mari care nu incap in memoria RAM sau in memoria virtuala pusa la dispozitie de catre sistemul gazda, este o sortare prin interclasare: se sorteaza intern secvente de articole din fisier si se interclaseaza succesiv aceste secvente ordonate de articole.
Exista variante multiple ale sortarii externe prin interclasare care difera prin numarul, continutul si modul de folosire al fisierelor, prin numarul fisierelor de lucru create.
O secventa ordonata de articole se numeste si "monotonie" ("run"). Faza initiala a procesului de sortare externa este crearea de monotonii. Un fisier poate contine o singura monotonie sau mai multe monotonii (pentru a reduce numarul fisierelor temporare). Interclasarea poate folosi numai doua monotonii ("2-way merge") sau un numar mai mare de monotonii ("multiway merge"). Dupa fiecare pas se reduce numarul de monotonii, dar creste lungimea fiecarei monotonii (fisierul ordonat contine o singura monotonie).
Crearea monotoniilor se poate face prin citirea unui numar de articole succesive din fisierul initial, sortarea lor (prin metoda quicksort) si scrierea secventei ordonate ca o monotonie in fisierul de iesire. Pentru exemplificare sa consideram un fisier ce contine articole cu urmatoarele chei (in aceasta ordine):
7, 6, 4, 8, 3, 5
Sa consideram ca se foloseste un buffer de doua articole (in practica sunt zeci, sute sau mii de articole intr-o zona tampon). Procesul de creare a monotoniilor:
Input Buffer Output
7,6 6,7
3 3,5 6,7 | 4,8 | 3,5
Crearea unor monotonii mai lungi (cu aceeasi zona tampon) se poate face prin metoda selectiei cu inlocuire ("replacement selection") astfel:
- Se alege din buffer articolul cu cea mai mica cheie care este mai mare decat cheia ultimului articol scris in fisier.
- Daca nu mai exista o astfel de cheie atunci se termina o monotonie si incepe o alta cu cheia minima din buffer.
- Se scrie in fisierul de iesire articolul cu cheia minima si se citeste urmatorul articol din fisierul de intrare.
Pentru exemplul anterior, metoda va crea doua monotonii mai lungi:
Input Buffer Output
7,6 6
4,8,3,5 7 6,7
8 4,8 6,7,8
3 4,3 6,7,8 | 3
5 4 6,7,8 | 3,4
- 5 6 | 3,4,5
Pentru reducerea timpului de sortare se folosesc zone buffer cat mai mari, atat la citire cat si pentru scriere in fisiere. In loc sa se citeasca cate un articol din fiecare monotonie, se va citi cate un grup de articole din fiecare monotonie, ceea ce va reduce numarul operatiilor de citire de pe disc (din fisiere diferite, deci cu deplasarea capetelor de acces intre piste disc).
Detaliile acestui proces pot fi destul de complexe, pentru a obtine performante cat mai bune.
3 Indexarea datelor
Datele ce trebuie memorate permanent se pastreaza in fisiere si baze de date. O baza de date reuneste mai multe fisiere necesare unei aplicatii, impreuna cu metadate ce descriu formatul datelor (tipul si lungimea fiecarui camp) si cu fisiere index folosite pentru accesul rapid la datele aplicatiei, dupa diferite chei.
Modelul principal utilizat pentru baze de date este modelul relational, care grupeaza datele in tabele, legaturile dintre tabele fiind realizate printr-o coloana comuna si nu prin adrese disc. Relatiile dintre tabele pot fi de forma 1 la 1, 1 la n sau m la n ("one-to-one", "one-to-many", "many-to-many"). In cadrul modelului relational exista o diversitate de solutii de organizare fizica a datelor, care sa asigure un timp bun de interogare (de regasire) dupa diverse criterii, dar si modificarea datelor, fara degradarea performantelor la cautare.
Cea mai simpla organizare fizica a unei baze de date ( in dBASE si FoxPro) face din fiecare tabel este un fisier secvential, cu articole de lungime fixa, iar pentru acces rapid se folosesc fisiere index. Metadatele ce descriu fiecare tabel (numele, tipul, lungimea si alte atribute ale coloanelor din tabel) se afla chiar la inceputul fisierului care contine si datele din tabel. Printre aceste metadate se poate afla si numele fisierului index asociat fiecarei coloane din tabel (daca a fost creat un fisier index pentru acea coloana).
Organizarea datelor pe disc pentru reducerea timpului de cautare este si mai importanta decat pentru colectii de date din memoria interna, datorita timpului mare de acces la discuri (fata de memoria RAM) si a volumului mare de date. In principiu exista doua metode de acces rapid dupa o cheie (dupa continut):
- Calculul unei adrese in functie de cheie, ca la un tabel "hash";
- Crearea si mentinerea unui tabel index, care reuneste cheile si adresele articolelor din fisierul de date indexat.
Prima metoda poate asigura cel mai bun timp de regasire, dar numai pentru o singura cheie si fara a mentine ordinea cheilor (la fel ca la tabele "hash").
Atunci cand este necesara cautarea dupa chei diferite (campuri de articole) si cand se cere o imagine ordonata dupa o anumita cheie a fisierului principal se folosesc tabele index, cate unul pentru fiecare camp cheie (cheie de cautare si/sau de ordonare). Aceste tabele index sunt realizate de obicei ca fisiere separate de fisierul principal, ordonate dupa chei.
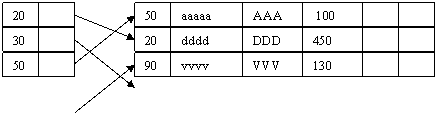
Un index contine perechi cheie-adresa, unde "adresa" este adresa relativa in fisierul de date a articolului ce contine cheia. Ordinea cheilor din index este in general alta decat ordinea articolelor din fisierul indexat; in fisierul principal ordinea este cea in care au fost adaugate articolele la fisier (mereu la sfarsit de fisier), iar in index este ordinea valorilor cheilor.
Id Adr Id Nume Marca Pret
![]()
![]()
|
|
![]()
Fisierul index este intotdeauna mai mic decat fisierul indexat, deoarece contine doar un singur camp din fiecare articol al fisierului principal. Timpul de cautare va fi deci mai mic in fisierul index decat in fisierul principal, chiar daca indexul nu este ordonat sau este organizat secvential. De obicei fisierul index este ordonat si este organizat astfel ca sa permita reducerea timpului de cautare, dar si a timpului necesar actualizarii indexului, la modificari in fisierul principal.
Indexul dat ca exemplu este un index "dens", care contine cate un articol pentru fiecare articol din fisierul indexat. Un index "rar", cu mai putine articole decat in fisierul indexat, poate fi folosit atunci cand fisierul principal este ordonat dupa cheia continuta de index (situatia cand fisierul principal este relativ stabil, cu putine si rare modificari de articole).
Orice acces la fisierul principal se face prin intermediul fiserului index "activ" la un moment dat si permite o imagine ordonata a fisierului principal (de exemplu, afisarea articolelor fisierului principal in ordinea din fisierul index).
Mai mult, fisierele index permit selectarea rapida de coloane din fisierul principal si "imagini" ("views") diferite asupra unor fisiere fizice; de exemplu, putem grupa coloane din fisiere diferite si in orice ordine, folosind fisierele index. Astfel se creeaza aparenta unor noi fisiere, derivate din cele existente, fara crearea lor efectiva ca fisiere fizice.
Un index dens este de fapt un dictionar in care valorile asociate cheilor sunt adresele articolelor cu cheile respective in fisierul indexat, dar un dictionar memorat pe un suport extern. De aceea, solutiile de implementare eficienta a dictionarelor ordonate au fost adaptate pentru fisiere index: arbori binari de cautare echilibrati (in diferite variante, inclusiv "treap") si liste skip.
Adaptarea la suport extern inseamna in principal ca un nod din arbore (sau din lista) nu contine o singura cheie ci un grup de chei. Mai exact, fiecare nod contine un vector de chei de capacitate fixa, care poate fi completat mai mult sau mai putin. La depasirea capacitatii unui nod se creeaza un nou nod.
Cea mai folosita solutie pentru fisiere index o constituie arborii B, in diferite variante (B+, B* s.a.).
4 Arbori B
Un arbore B este un arbore de cautare multicai echilibrat, adaptat memoriilor externe cu acces direct. Un arbore B de ordinul n are urmatoarele proprietati:
- Radacina fie nu are succesori, fie are cel putin doi succesori.
- Fiecare nod interior (altele decat radacina si frunzele) au intre n/2 si n succesori.
- Toate caile
de la radacina la
Fiecare nod ocupa un articol disc (preferabil un multiplu de sectoare disc) si este citit integral in memorie. Sunt posibile doua variante pentru nodurile unui arbore B:
- Nodurile
interne contin doar chei si pointeri la alte noduri, iar datele asociate
fiecarei chei sunt memorate in
- Toate nodurile au aceeasi structura, continand atat chei cat si date asociate cheilor.
Fiecare nod (intern) contine o secventa de chei si adrese ale fiilor de forma urmatoare:
p[0], k[1], p[1], k[2], p[2],,k[m], p[m] ( n/2 <= m <= n)
unde k[1]<k[2]<k[m] sunt chei, iar p[0],p[1],..p[m] sunt legaturi catre nodurile fii (pseudo-pointeri, pentru ca sunt adrese de octet in cadrul unui fisier disc).
In practica, un nod contine zeci sau sute de chei si adrese, iar inaltimea arborelui este foarte mica (rareori peste 3). Pentru un arbore cu un milion de chei si maxim 100 de chei pe nod sunt necesare numai 3 operatii de citire de pe disc pentru localizarea unei chei, daca toate nodurile contin numarul maxim de chei): radacina are 100 de fii pe nivelul 1, iar fiecare nod de pe nivelul 1 are 100 de fii pe nivelul 2, care contin cate 100 de chei fiecare.
Toate cheile din subarborele cu adresa p[0] sunt mai mici decat k[1], toate cheile din subarborele cu adresa p[m] sunt mai mari decat k[m], iar pentru orice 1<=i<n cheile din subarborele cu adresa p[i] sunt mai mari sau egale cu k[i] si mai mici decat k[i+1].
Arborii B pot fi priviti ca o generalizare a arborilor 2-3-4 si cunosc mai multe variante de implementare:
- Date si in nodurile interioare sau date numai in noduri de pe ultimul nivel.
- Numarul minim de chei pe nod si strategia de spargere a nodurilor (respectiv de contopire noduri cu acelasi parinte): n/2 sau 2n/3 sau 3n/4.
Exemplu de arbore B de ordinul 4 ( asteriscurile reprezinta adrese de blocuri disc):
* 18 *
____________| |__________
In desenul anterior nu apar si datele asociate cheilor.
Arborii B au doua utilizari principale:
- Pentru dictionare cu numar foarte mare de chei, care nu pot fi pastrate integral in memoria RAM;
- Pentru fisiere index asociate unor fisiere foarte mari (din baze de date), caz in care datele asociate cheilor sunt adrese disc din fisierul mare indexat.
Cu cat ordinul unui arbore B (numarul maxim de succesori la fiecare nod) este mai mare, cu atat este mai mica inaltimea arborelui si deci timpul mediu de cautare.
Cautarea unei chei date intr-un arbore B seamana cu cautarea intr-un arbore binar de cautare BST, dar arborele este multicai si are nodurile pe disc si nu in memorie.
Nodul radacina nu este neaparat primul articol din fisierul arbore B din cel putin doua motive:
- Primul bloc (sau primele blocuri, functie de dimensiunea lor) contin informatii despre structura fisierului (metadate): dimensiune bloc, adresa bloc radacina, numarul ultimului bloc folosit din fisier, dimensiune chei, numar maxim de chei pe bloc, s.a.
- Blocul radacina se poate modifica in urma cresterii inaltimii arborelui, consecinta a unui numar mai mare de articole adaugate la fisier.
Fiecare bloc disc trebuie sa contina la inceput informatii cum ar fi numarul de chei pe bloc si (eventual) daca este un nod interior sau un nod frunza.
Insertia unei chei intr-un arbore B incepe prin cautarea blocului de care apartine noua cheie si pot apare doua situatii:
- mai este loc in blocul respectiv, cheia se adauga si nu se fac alte modificari in arbore
- nu mai este loc in bloc, se sparge blocul in doua, mutand jumatate din chei in noul bloc alocat si se introduce o noua cheie in nodul parinte (daca mai este loc). Acest proces de aparitie a unor noi noduri se poate propaga in sus pana la radacina, cu cresterea inaltimii arborelui B.
Exemplu de adaugare a cheii 23 la arborele anterior:
* 18 28 *
____________| |___ |____________________
Propagarea in sus pe arbore a unor modificari de blocuri inseamna recitirea unor blocuri disc, deci revenirea la noduri examinate anterior. O solutie mai buna este anticiparea umplerii unor blocuri: la adaugarea unei chei intr-un bloc se verifica daca blocul este plin si se "sparge" in alte doua blocuri.
Eliminarea unei chei dintr-un arbore B poate antrena comasari de noduri daca raman prea putine chei intr-un nod (mai putin de jumatate din capacitatea nodului).
Vom ilustra evolutia unui arbore B cu maxim 4 chei si 5 succesori pe nod (practic un arbore 2-3-4) la adaugarea unor chei din doua caractere cu valori succesive: 01, 02, 09, 10, 11,..,19 prin cateva cadre din filmul acestei evolutii. Toate nodurile contin chei si date, iar articolul 0 din fisier contine metadate; primul articol cu date este 1 (notat "a1"), care initial este si radacina arborelui.
a1=[01,- ,- ,- ] [01,02,03,- ] (split)
![]()
![]()
![]()
![]() a3= [03
,- ,- ] a3=[03,- ,- ,- ]
a3= [03
,- ,- ] a3=[03,- ,- ,- ]
(split)
a1=[01,02,- ,- ] a2=[04,05,- ,- ] a1=[01,02,- ,- ] a2=[04,05,06,07]
![]()
![]()
![]() a3= [03
,- ,- ]
a3= [03
,- ,- ]
a1=[01,02,- ,- ] a2=[04,05,- ,- ] a4=[07,08,- ,- ]
![]()
![]()
![]()
![]()
![]() a3 03, 06, 09, 12 ]
a3 03, 06, 09, 12 ]
a1=[01,02,- ,- ] a2=[04,05,- ,- ] a4=[07,08,- ,- ] a5=[10,11,- ,- ] a6=[13,14,15,16]
a9 09,- ,- ,- ]
![]()
![]()
a3=[03,06,- ,- ] a8=[12,15,- ,- ]
![]()
![]()
![]()
![]()
![]()
![]()
a1=[01,02,- ,- ] a2=[04,05,- ,- ] a4=[07,08,- ,- ] a5=[10,11,- ,- ] a6=[13,14,- ,- ] a7=[16,17,- ,- ]
Secventa de chei ordonate este cea mai rea situatie pentru un arbore B, deoarece raman articole numai pe jumatate completate (cu cate 2 chei), dar am ales-o pentru ca ea conduce repede la noduri pline si care trebuie sparte ("split"), deci la crearea de noi noduri. Crearea unui nod nou se face mereu la sfarsitul fisierului (in primul loc liber) pentru a nu muta date dintr-un nod in altul (pentru minimizarea operatiilor cu discul).
Vom prezenta cateva functii pentru operatii cu un arbore B si structurile de date folosite de aceste functii:
// elemente memorate in nodurile arborelui B
typedef struct Item;
// structura unui nod de arbore B (un articol din fisier, inclusiv primul articol)
typedef struct BTNode;
// zona de lucru comuna functiilor
typedef struct Btree;
In aceasta varianta intr-un nod nu alterneaza chei si legaturi; exista un vector de chei ("keys") si un vector de legaturi ("link"). link[i] este adresa nodului ce contine chei cu valori mai mici decat keys[i], iar link[i+1] este adresa nodului cu chei mai mari decat keys[i]. Pentru n chei sunt n+1 legaturi la succesori. Prin "adresa nod" se intelege aici pozitia in fisier a unui articol (relativ la inceputul fisierului).
Inaintea oricarei operatii este necesara deschiderea fisierului ce contine arborele B, iar la inchidere se rescrie antetul (modificat, daca s-au facut adaugari sau stergeri).
Cautarea unei chei date in arborele B se face cu functia urmatoare:
// cauta cheia 'key' si pune elementul care o contine in 'item'
int retrieve(Btree & bt, char* key, Item & item)
else // daca nu este in nodul curent
rec = bt.node.link[idx + 1]; // cauta in subarborele cu rad. "rec"
}
return found;
}
Functia de cautare a unei chei intr-un nod :
// cauta cheia 'key' in nodul curent si pune in 'idx' indicele din nod
// unde s-a gasit (rezultat 1) sau unde poate fi cautata (rezultat 0)
// 'idx' este -1 daca 'key' este mai mica decat prima cheie din bloc
int search( Btree & bt, KeyT key, int & idx)
return found; // cheie negasita, dar mai mare ca keys[idx].key
}
Adaugarea unui nou element la un arbore B este realizata de cateva functii:
- "addItem" adauga un element dat la nodul curent (stiind ca este loc)
- "find" cauta nodul unde trebuie adaugat un element, vede daca nodul este plin, creeaza un nod nou si raporteaza daca trebuie creat nod nou pe nivelul superior
- "split" sparge un nod prin crearea unui nod nou si repartizarea cheilor in mod egal intre cele doua noduri
- "insert" foloseste pe "find" si, daca e nevoie, creeaza un alt nod radacina.
void insert(Btree & bt, Item item)
bt.items++; // creste numarul de elemente din arbore
}
// determina nodul unde trebuie plasat 'item': 'moveUp' este 1 daca
// 'newItem' trebuie plasat in nodul parinte (datorita spargerii unui nod)
// 'moveUp' este 0 daca este loc in nodul gasit in subarb cu rad. 'croot'
void find( Btree & bt, Item item, int croot, int & moveUp,Item & newItem,
int & newRight)
else
else
}
}
}
// sparge blocul curent (din memorie) in alte 2 blocuri cu adrese in
// croot si *newRight; 'item' a produs umplerea nodului, 'newItem'
// se muta in nodul parinte
void split(Btree & bt, Item item, int right, int croot, int idx, Item & newItem,
int & newRight)
rNode.count = MaxKeys - median;
bt.node.count = median; // is then incremented by addItem
// put CurrentItem in place
if (idx < MinKeys)
addItem(item, right, bt.node, idx + 1);
else
addItem(item, right, rNode, idx - median + 1);
newItem = bt.node.keys[bt.node.count - 1];
rNode.link[0] = bt.node.link[bt.node.count];
bt.node.count--;
fseek(bt.file, croot*bt.size, 0);
fwrite(&bt.node, bt.size,1,bt.file);
bt.nodes++;
newRight = bt.nodes;
fseek(bt.file, newRight * bt.size, 0 );
fwrite( &rNode, bt.size,1,bt.file);
}
// adauga 'item' la nodul curent 'node' in pozitia 'idx'
// prin deplasarea la dreapta a elementelor existente
void addItem(Item item, int newRight, BTNode & node, int idx)
node.keys[idx] = item;
node.link[idx + 1] = newRight;
node.count++;
}
Exemplu de program pentru crearea unui arbore B, urmata de cautarea unor chei in arborele creat:
void main(void)
while ( fscanf (txt,'%s%s',item.key,item.data)==2)
Bclose (&bt);
// interogare
Bopen(&bt,'r', 'btree.dat');
puts ( 'Cheie cautata : ');
while ( scanf('%s',key)==1)
}
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1406
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved