Sirul si tabloul

Sirul si tabloul

Definitia 3.2

Un sir este o multime ordonata de elemente, care apartin unei clase de simboluri elementare.

Lungimea unui sir este egala cu numarul de elemente care compun sirul. Tipul unui sir este tipul caracter. Pot exista siruri de biti, siruri de cifre, siruri de litere, siruri de cifre si litere, siruri de caractere. Cele mai importante operatii definite pe siruri sunt operatia de concatenare si operatia de comparare.

Definitia 3.3

Un tablou este o multime ordonata de elemente de acelasi tip.

Ordonarea elementelor intr-un tablou este folosita pentru a identifica elementele in cadrul tabloului, in care scop se utilizeaza un ansamblu de indici. Numarul de indici folositi pentru a identifica elementele unui tablou constituie numarul de dimensiuni al tabloului. Astfel, exista tablouri cu o dimensiune (vectori), tablouri cu doua dimensiuni (matrice) etc.

Fiecarui element al unui tablou i se va aloca o zona de memorie numita locatie, lungimea acestei locatii fiind functie de tipul tabloului. Elementele unui vector vor ocupa in ordine locatii succesive de memorie. Pentru reprezentarea unei matrice se pot folosi doua metode:

memorarea succesiva pe linii a elementelor;

memorarea succesiva pe coloane a elementelor.

Fie N₁,,N_p multimi total ordonate cu | N_i | = n_i , i = 1,.,p. Pentru simplificare, vom nota in acelasi mod (<, ≤) cele p relatii de ordine. Fie multimea N = N₁ x x N_p, si x, y I N , x = (x₁, , x_p), y = (y₁, , y_p), x_i, y_i N_i, i=1,,p. Pe multimea N se pot introduce urmatoarele doua relatii de ordine:

relatia de ordine lexicografica, conform careia avem x ≤ y daca x = y sau x < y ( adica k astfel incat x_i = y_i, i = 1, , k-1, x_k < y_k );

relatia de ordine invers lexicografica, conform careia x ≤ y daca x = y sau x < y ( adica k astfel incat x_k < y_k, x_i = y_i , i = k+1, , p).

Observam ca pentru o matrice cu m linii si n coloane ordinea de memorare pe linii corespunde ordinii lexicografice pe N = N₁ x N₂ = x , iar ordinea de memorare pe coloane corespunde relatiei de ordine invers lexicografice pe aceeasi multime.

Fie T(n₁, n₂, , n_p) un tablou p dimensional avand limitele maximale pentru indicii i₁, i₂, , i_p respectiv pe n₁, n₂, , n_p. Fie N_k = , k = 1, , p, n = n₁ n₂ n_{p ,} N_n = . Definim bijectia

r₁ : N₁ x x N_p-1 x N_p N_n

r₁(i₁, , i_p-1, i_p) = i_p + (i_p-1 - 1)n_p + (i_p-2 - 1)n_pn_p-1 + + (i₁ - 1)n_pn₂

Numarul r₁(i₁, , i_p-1, i_p) numit rangul elementului T(i₁, , i_p-1, i_p) reprezinta numarul locatiei de memorie a elementului in memorarea tabloului conform relatiei de ordine invers lexicografice pe multimea N₁ x x N_p-1 x N_p.

Analog definim bijectia

r₂ : N₁ x N₂ x x N_p N_n

r₂(i₁, i₂, , i_p) = i₁ + (i₂ - 1)n₁ + (i₃ - 1)n₁n₂ + + (i_p - 1)n₁n₂n_p-1

Numarul r₂(i₁, i₂, , i_p) numit rangul elementului T(i₁, i₂, , i_p) reprezinta numarul locatiei de memorie a elementului in memorarea tabloului conform relatiei de ordine invers lexicografice pe multimea N₁ x N₂ x x N_p.

Exemplul 3.1

N1 = N2 = p = 2, n1 = 3, n2 = 4, n = 12 N12 =

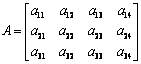
Memorarea pe linii

i 2 3 4 5 6 7 8 9 10 11 12

x_i (1,1) (1,2) (1,3) (1,4) (2,1) (2,2) (2,3) (2,4) (3,1) (3,2) (3,3) (3,4)

Avem x_i < x_i , i = 1, ,11 in ordinea lexicografica; x_i = (x_i1, x_i2)

r₁ : N₁ x N₂ N₁₂, r₁(i₁, i₂) = i₂ + (i₁-1)n₂

r₁(2, 3) = 3 + (2-1)*4 = 7

Memorarea pe coloane

i 1 2 3 4 5 6 7 8 9 10 11 12

x_i (1,1) (2,1) (3,1) (1,2) (2,2 ) (3,2) (1,3) (2,3) (3,3 ) (1,4) (2,4) (3,4)

Avem x_i < x_i , i = 1, , 11 in ordinea invers lexicografica; x_i = (x_i1, x_i2)

r₂ : N₁ x N₂ N₁₂, r₂(i₁, i₂) = i₁ + (i₂-1)n₁

r₂(2, 3) = 2 + (3 - 1) * 3 = 8