Sortare

Sortare

Problema sortarii consta in a ordona crescator elementele vectorului a = (a(1), , a(n)). Trei dintre cei mai cunoscuti algoritmi eficienti care rezolva problema sortarii sunt: sortarea prin interclasare (MergeSort), sortarea rapida (QuickSort) si sortarea folosind heapuri (HeapSort). Primii doi algoritmi se bazeaza pe metoda divide et impera.

1 Sortarea prin interclasare (MergeSort)

Sortarea prin interclasare consta din urmatorii pasi principali:

• imparte sirul dat in doua subsiruri;
• rezolva recursiv fiecare din cele doua subprobleme;
• interclaseaza cele doua subsiruri sortate pentru a obtine sirul sortat.

Descompunerea unui sir in doua subsiruri are loc pana cand avem de sortat subsiruri de unul sau doua elemente. Algoritmul sortarii prin interclasare este prezentat in PROGRAM SORTINT. Procedura SORT sorteaza un sir de maxim doua elemente, procedura DIVIMP implementeaza    strategia metodei divide et impera si procedura INTERCLAS interclaseaza cele doua subsiruri sortate pentru a obtine sirul sortat.

Teorema 5.2

Algoritmul sortarii prin interclasare are complexitatea O(n log n)

Demonstratie

Este cazul s=2, n₀=2 din teoria generala a metodei divide et impera si conform Teoremei 4.6 algoritmul are complexitatea O(n log n).

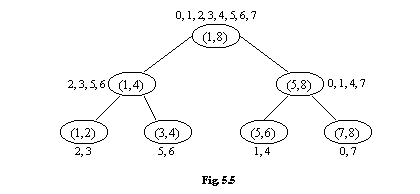
Exemplul 5.4

a=(a(1), a(2), a(3), a(4), a(5), a(6), a(7), a(8)) = (3, 2, 5, 6, 4, 1, 0, 7).

PROCEDURE SORT(A, P, Q);

BEGIN

IF A_P>A_Q

THEN BEGIN

X:=A_P; A_P:=A_Q; A_Q:=X;

END;

END;

PROCEDURE DIVIMP(A, P, Q);

BEGIN

IF (Q-P)≤1

THEN SORT(A, P, Q)

ELSE BEGIN

M:= (P+Q)/2

DIVIMP(A, P, M);

DIVIMP(A, M+1, Q);

INTERCLAS(A, P, Q, M);

END;

END;

PROGRAM SORTINT;

BEGIN

ARRAY A(N);

READ N, A_I, 1 ≤ I ≤ N;

DIVIMP(A, 1, N);

WRITE A_I, 1 ≤ I ≤ N;

END.

Codul sursa al programului care implementeaza metoda sortarii prin interclasare este urmatorul:

#include<stdio.h>

//merge sort

void interclasare(int a[20], int p, int m, int q)

void sort(int a[20], int p, int q)

void merge(int a[20], int p, int q)

void mergesort(int a[20], int n)

void afisare(int a[20], int n)

void main()

mergesort(a,n);

afisare(a,n);

2 Sortarea rapida (QuickSort)

Sortarea rapida (QuickSort) consta in pozitionarea elementului a(p) al subsirului (a(p), , a(q)) pe o pozitie m, prin interschimbari de elemente ale subsirului, astfel incat a(i) ≤ a(m) ≤ a(j), i=1, , m-1, j=m+1, , q. Continuam acest procedeu cu subsirurile (a(p), , a(m-1)) si (a(m+1), , a(q)) independent unul de altul. Impartirea in subsiruri ne sugereaza utilizarea metodei divide et impera dar fara combinarea rezultatelor.

Evident ca dupa pozitionarea elementului a(p) pe pozitia m va ramane pe aceasta pozitie in cadrul sirului sortat. Aceasta reprezinta esenta algoritmului sortarii rapide , care este prezentat in PROGRAM SORTRAPID. Procedura PART partitioneaza un sir in doua subsiruri conform precizarilor de mai sus. Procedura DIVIMP implementeaza strategia metodei divide et impera fara combinarea rezultatelor.

In cazul cel mai defavorabil, cand s=2, n₀=2, complexitatea algoritmului este O(n log n). Se poate demonstra ca timpul mediu al algoritmului este O(n log n). In cazul cel mai defavorabil, cand sirul este deja sortat (pozitionarea se face dupa fiecare element) complexitatea algoritmului este O(n²).

PROCEDURE PART(A, P, Q, M)

BEGIN

I:=P-1; J:=Q+1; B:=0; EP:=A_P;

REPEAT

REPEAT

I:=I+1;

UNTIL A_I≥EP;

REPEAT

J:=J-1;

UNTIL A_J≤EP;

IF (I<J)

THEN BEGIN

X:=A_I; A_I:=A_J; A_J:=X;

END

ELSE BEGIN

B:=1; M:=J;

END;

UNTIL B=1;

END;

PROCEDURE DIVIMP(P, Q);

BEGIN

IF(P<Q)

THEN BEGIN

PART(A, P, Q, M);

DIVIMP(P,M);

DIVIMP(M+1, Q);

END;

END;

PROGRAM SORTRAPID;

BEGIN

ARRAY A(N);

READ N, A_I, 1 ≤ I ≤ N;

DIVIMP(1, N);

WRITE A_I, 1 ≤ I ≤ N;

END.

Observatia 5.2

In practica se dovedeste ca algoritmul sortarii rapide este cel mai eficient algoritm de sortare.

Codul sursa corespunzator este urmatorul:

int part(int a[20], int p, int q)

else

return j;

}

void quick(int a[20], int p, int q)

void quicksort(int a[20], int n)

void afisare(int a[20], int n)

void main()

mergesort(a,n);

afisare(a,n);

3 Sortarea folosind heapuri (HeapSort)

Definitia 5.1 Spunem ca un arbore binar este aproape complet daca fiecare nod cu exceptia celor de pe ultimul nivel are exact doi descendenti si toti descendentii de pe ultimul nivel sunt completati de la stanga la dreapta.

Definitia 5.2 Spunem ca un nod are proprietatea de heap daca descendentii lui directi au valori mai mici decat el.

Definitia 5.3 Un arbore binar aproape complet are proprietatea de heap daca toate nodurile sale au proprietatea de heap.

Definitia 5.4 Numim semi-heap un arbore binar aproape complet in care toate nodurile cu exceptia nodului radacina indeplinesc proprietatea de heap.

Datorita faptului ca este un arbore binar aproape complet un heap se poate memora foarte usor cu ajutorul unui vector, astfel incat pentru un nod i descendentii sai directi sunt 2*i si 2*i+1. De asemenea este usor de observat ca pentru un nod i parintele lui este [i/2].

Avantajul acestei metode este ca nu sunt necesari pointeri pentru a reprezenta o astfel de structura.

Un exemplu de astfel de heap este prezentat in figura 5.6:

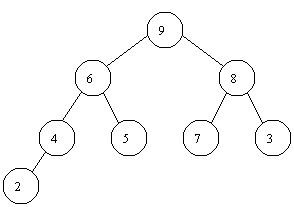
Fig. 5.6

Acest heap se poate memora intr-un vector a prin parcurgerea nodurilor de sus in jos si de la stanga la dreapta: a=(9, 6, 8, 4, 5, 7, 3, 2).

Ideea sortarii folosind aceasta metoda se bazeaza pe faptul ca la orice moment este foarte usor sa luam elementul radacina, care este cel mai mare element din heap, il interschimam cu elementul de pe    ultima pozitie din sir, dupa care pentru semi-heap-ul rezultat se reface proprietatea de heap.

Refacerea proprietatii de heap pentru un semi-heap este usoara. Daca radacina are deja proprietatea de heap, atunci am terminat. Altfel, consultam descendentii/ descendentul nodului radacina si interschimbam radacina cu nodul care are valoarea mai mare, dupa care, pentru acest nod se verifica daca respecta proprietatea de heap. Se procedeaza astfel pana cand gasim un nod care respecta proprietatea de heap sau se ajunge la un nod frunza (nodul i este frunza daca 2*i este mai mare decat dimensiunea heapului).

Aceasta idee este implementata in urmatoarea procedura:

(1) PROCEDURE DOWNHEAP(A,I)

(2) BEGIN

ST=2*I

DR=2*I

IF ST≤N AND A_ST>A_I THEN

MAX:=ST

ELSE

MAX:=I

IF DR≤N AND A_DR>A_MAX THEN

MAX:=DR;

(11) IF MAX≠I THEN

BEGIN

AUX:=A_I;

A_I:=A_MAX;

A_MAX:=AUX;

DOWNHEAP(A,MAX);

END;

(18)END;

Tot cu ajutorul acestei proceduri se poate reconstrui heapul in situatia in care avem un arbore binar aproape complet pentru care nici un nod nu respecta proprietatea de heap. Pentru a realiza acest lucru se parcurg toate nodurile interne (numarul nodului este mai mic sau egal decat jumatate din dimensiunea heapului) si pentru fiecare astfel de nod se apeleaza procedura de refacere a unui heap pornind de la un semi-heap.

Algoritmul este implementat in urmatoare procedura:

(1)PROCEDURE BUILDHEAP(A,N)

(2)BEGIN

(3) FOR i:= n/2 DOWNTO 1 DO

DOWNHEAP(A,i);

(5)END;

Metoda de sortare Heap - Sort se bazeaza pe cei 2 algoritmi prezentati anterior. Astfel, primul pas este sa se construiasca un heap, dupa care in mod repetat se interschimba primul element din sir (maximul din heap) cu ultimul element din heap, dupa care dimensiunea heap-ului se considera cu unul mai mica si se reface proprietatea de heap pentru noul sir. Se repeta acest lucru pana cand se ajunge la un heap de dimensiune 1.

Algoritmul de sortare este urmatorul:

(1) PROCEDURE HEAPSORT(A,n)

(2) BEGIN

BUILDHEAP(A,n);

FOR I:=N DOWNTO 2 DO

BEGIN

AUX:=A₁;

A₁:=A_I;

A_I:=AUX;

DOWNHEAP(A,1);

END;

(11)END;

Teorema 5.3

Sortarea folosind metoda Heap - Sort are complexitatea O(nlog(n)).

Demonstratie

Un arbore binar aproape complet cu n noduri are adancimea cel mult log(n), de unde se poate afirma ca pentru a reconstrui un heap dintr-un semi-heap este nevoie de cel mult log(n) operatii. Cum sortarea prin metoda heap-sort apeleaza de cel mult n ori reconstruirea heapului, rezulta faptul ca complexitatea metodei este cel mult O(nlog(n)).

Observatia 5.3

Sortarea folosind metoda Heap Sort este o sortare "in place", ceea ce inseamna ca pentru a sorta elementele sirului nu este nevoie de un alt sir sortarea facandu-se pe loc.

Observatia 5.4

Aceasta metoda de sortare este nu este stabila, in sensul in care in momentul in care se face sortarea elementele care ar fi pe pozitiile lor corecte nu-si pastreaza pozitiile lor initiale.

Algoritmul in limbajul C corespunzator acestei metode de sortare este urmatorul:

#include<stdio.h>

#include<conio.h>

void downheap(int a[20], int n, int i)

void buildheap(int a[20], int n)

void heapsort(int a[20], int n)

void main()

heapsort(a,n);

for(i=1;i<=n;i++)

printf('%d ',a[i]);