| CATEGORII DOCUMENTE |
Tipul float
Acest tip de reprezentare este de tip real, fiind cunoscut si ca reprezentare in virgula mobila (floating point). Acest tip descrie mecanismul de baza prin care se manipuleaza datele reale. Conceptul fundamental este acela de notatie stiintifica, prin care orice numar se poate exprima ca un numar zecimal (deci, cu punct zecimal) multiplicat cu o putere a lui zece sau ca un numar real binar (cu punct binar) multiplicat cu o putere a lui 2.
![]()
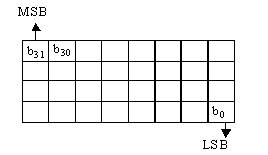
Se observa cum stocarea in calculator a unei date floating-point necesita trei parti:
bitul de semn (sign)
mantisa, fractia (significand)
exponent (exponent)
Folosind formatul specific I80386, in limbajul C se disting trei tipuri de date reale:
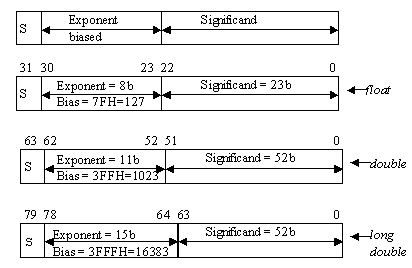
float , cu reprezentare pe 4 octeti (32 biti, double word)
double, cu reprezentare pe 8 octeti (64 biti, quad word)
long double, cu reprezentare pe 10 octeti (80 biti, ten word)
Tipurile float si double sunt formate pentru numere reale ce exista numai in memorie. Cand un astfel de numar este incarcat de procesor in stiva pentru numere reale (flotante) pentru prelucrare sau ca rezultat al prelucrarii, el este automat convertit la formatul long double (sau extended).
In cazul in care acest numar se stocheaza in memorie, el se converteste la tipul float sau double. Toate cele trei subtipuri reale au un format comun, care va fi prezentat in continuare. Ceea ce le deosebeste este numarul de biti alocati pentru exponent si pentru mantisa, precum si interpretarea bitilor mantisei (significand).
Semnul are alocat in toate formatele un singur bit: 0 pentru numere pozitive si 1 pentru numere negative.
Marimea campului exponent variaza cu formatul si valoarea sa determina cati biti se muta la dreapta sau la stanga punctului binar.
Campul significand este analogul mantisei in notatia stiintifica. El contine totii bitii semnificativi ai reprezentarii, deci bitii semnificativi atat ai partii intregi cat si ai partii fractionare cu singura restrictie ca acesti biti sa fie consecutivi. Deoarece punctul binar este mobil, cu cat sunt mai multi biti alocati partii intregi, cu atat vor fi mai putini pentru partea fractionara si invers. Cu cat formatul este mai larg, cu atat se vor reprezenta mai precis numerele.
Pentru a salva un spatiu
pretios de stocare, nici unul dintre cele trei formate float nu
stocheaza zerouri nesemnificative.
De exemplu, pentru numarul ![]() campul significand va stoca numarul 101, nu si cele 4 zerouri
nesemnificative ale partii fractionare. Pentru a salva si mai mult spatiu,
pentru formatele float si double campul significand nu va contine primul bit semnificativ care obligatoriu este
1. Castigand acest bit (numit bit phantom), se dubleaza gama de reprezentare. Formatul long
double va contine totusi bitul
de semn 1 cel mai semnificativ. Punctul binar se pune exact inaintea
primului bit din campul significand, adica dupa bitul 1 implicit (phantom). In cazul long double,
se aplica dupa primul bit 1.
campul significand va stoca numarul 101, nu si cele 4 zerouri
nesemnificative ale partii fractionare. Pentru a salva si mai mult spatiu,
pentru formatele float si double campul significand nu va contine primul bit semnificativ care obligatoriu este
1. Castigand acest bit (numit bit phantom), se dubleaza gama de reprezentare. Formatul long
double va contine totusi bitul
de semn 1 cel mai semnificativ. Punctul binar se pune exact inaintea
primului bit din campul significand, adica dupa bitul 1 implicit (phantom). In cazul long double,
se aplica dupa primul bit 1.
Pentru a usura operarea cu aceste numere, campul exponent nu este stocat ca un numar intreg cu semn, ci este decalat (normalizat, cu bias) pentru a reprezenta numai numere pozitive (deci exponentul este interpretat ca numar natural fara semn). Biasul adaugat se scade pentru a afla exponentul exact. Avantajul exponentului decalat consta, pe langa faptul ca nu mai are nevoie de bit de semn, in faptul ca pentru a compara doua numere reale putem incepe prin compararea bitilor pornind de la MSB catre LSB, cel mai mare fiind cel care are 1 la primul bit diferit. Se decide astfel foarte rapid care numar este cel mai mare. Ca exemplu, sa consideram un format float in care se stocheaza:
Sign = 0
Exponent = 10000010 = 13010
Significand = 1001000.00
Valoarea reala a exponentului va fi 130 - 127 = 3
Bitii campului significand se obtin adaugand MSB phantom, deci acestia vor fi 1100100000
Numarul real care s-a stocat este:
0.11001000 x 24 = 1100.1 =12.5
Reprezentarea interna a numarului 12.5, pe 4 octeti (float), este urmatoarea:

Cu alte cuvinte, putem spune ca reprezentarea interna a numarului real 12.5 este (in format hexazecimal):
![]()
In cazul in care dorim sa reprezentam numarul negativ -12.5, singurul bit care se va modifica va fi bitul de semn, care devine 1. Astfel, reprezentarea interna in format float a numarului negativ real -12.5 este:

![]()
Daca numarul 12.5 se reprezinta in formatul double, deci pe 8 octeti, atunci reprezentarea sa interna se va realiza astfel:
bitul de semn va fi 0
exponentul nu va mai fi pe 8 biti ca la tipul float, ci pe 11 biti, deci se va schimba si bias, care va fi 1023. Atunci:
![]()
significand va fi acelasi ca la tipul float, dar reprezentat pe 52 de biti

![]()
Retinem ca la numere reale numai bitul de semn indica daca numarul este pozitiv sau negativ, mantisa si exponentul se reprezinta ca numere naturale fara bit de semn. Formatele prezentate mai sus respecta standardul IEEE 754 de reprezentare a interna a numerelor reale in computere.
Se poate pune o intrebare legitima: de ce bias-ul in cazul float spre exemplu este 127? Pentru a raspunde la aceasta intrebare, putem face urmatorul rationament:
exponentul
cu semn este reprezentat pe 8 biti,
deci este in gama de reprezentare ![]() .
.
pentru a obtine un exponent pozitiv, adaugam numarul 128.
deoarece bitul phantom nu este reprezentat, exponentul trebuie micsorat cu o unitate pentru a indica unde anume se pozitioneaza exact punctul binar.
Exponent pozitiv = exponent +128 - 1 = exponent + bias
de unde rezulta evident faptul ca bias = 127 in cazul tipului float.
In final sa analizam un exemplu de procesare a produsului a doua numere reale. Vrem sa calculam valoarea 5.25 x 1.5. Pentru aceasta, vom scrie cei doi factori ai produsului in forma:


![]()
Se observa cum campurile exponent si significand sunt procesate separat, in final corelandu-se forma de reprezentare interna.
Game de reprezentare pentru numerele reale
Gama de reprezentare pentru fiecare din tipurile reale prezentate mai sus se calculeaza luand in considerare cel mai mare numar si cel mai mic numar posibil a fi scris in respectiva reprezentare. Astfel, exponentul este decisiv pentru gama de reprezentare.
La tipul float, avem
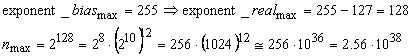
Valoarea maxima exacta, calculata fara a aproxima ca mai sus:
![]() este
este ![]()
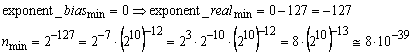
Valoarea
pozitiva minima exacta este ![]()
La tipul double vom obtine:
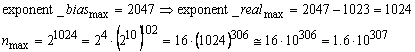
Valoarea maxima
exacta este ![]()
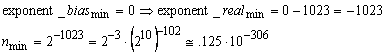
Valoarea pozitiva minima exacta este ![]()
Efectuand aceleasi consideratii si calcule pentru tipul long double, vom obtine 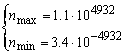
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1782
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved