NOTIUNI GENERALE.

Obiectul si importanta topografiei in domeniul tehnic.

Nevoia de cunoastere, caracteristica esentiala a omenirii, dar mai ales necesitatea ca suma cunostintelor acumulate in timp sa fie transmisa generatiilor viitoare, s-a facut simtita si in domeniul masuratorilor terestre atat prin gasirea modalitatilor de reprezentare a unor zone prin care oamenii au calatorit cat si a celor in care isi desfasurau activitatea in mod curent. Sunt cunoscute necesitatile omenirii pentru satisfacerea cerintelor militare, economice, de navigatie, religioase, etc.

Evolutia in timp a masuratorilor terestre a fost conditionata de dezvoltarea stiintelor exacte - matematica si fizica. Instrumentul teoretic al masuratorilor terestre este furnizat de matematica prin principiile si metodele de prelucrare a masuratorilor, instrumentele necesare observatiilor sunt construite pe baza cunostintelor de mecanica, optica si electronica, astronomia permite obtinerea datelor primare necesare prelucrarii retelelor de sprijin pe suprafete mari si stabilirea formei si dimensiunilor Pamantului, pentru ca la sfarsit sa obtinem imaginea micsorata a zonei de interes prin intermediul cunostintelor de cartografie.

Respectarea cerintelor privitoare la fidelitatea reprezentarii pe harta a formelor naturale existente in teren nu se poate face fara legatura cu geografia, geologia si geomorfologia. Cunoasterea geografiei permite o tratare corespunzatoare a elementelor naturale ale terenului cum ar fi relieful, vegetatia, natura solurilor, hidrografia, in timp ce apeland la geologie si geomorfologie se ajunge la formele reliefului si legile de modificare a lor.

Domeniul masuratorilor terestre se poate imparti in urmatoarele ramuri principale:

geodezia - care se ocupa cu studiul, masurarea si determinarea formei si dimensiunilor globului pamantesc sau a unor portiuni intinse ale acestuia. Pentru a se realiza acest lucru, pe suprafata terestra se determina coordonatele spatiale ale unor puncte care, prin unirea din aproape in aproape, determina varfurile unor triunghiuri. Odata determinate coordonatele geografice sau rectangulare ale acestor puncte, acestea devin puncte de sprijin pentru toate celelalte masuratori terestre. Totalitatea acestor puncte alcatuieste reteaua de puncte geodezice. Datorita suprafetei mari pe care se desfasoara aceste lanturi de triunghiuri, este necesar ca la prelucrarea masuratorilor sa se tina seama de influenta curburii Pamantului.

topografia - care, pornind de la datele furnizate de geodezie (coordonatele unor puncte intr-un sistem unitar, care insa nu delimiteaza si nu reprezinta detalii din teren), sa stabileasca pozitia relativa a obiectelor din teren si sa le reprezinte pe harti sau planuri. Caracteristic pentru lucrarile topografice este ca acestea se desfasoara pe suprafete relativ mici in care influenta curburii Pamantului este considerata neglijabila.

fotogrametria - poate fi considerata ca o tehnica noua in masuratorile terestre in sensul ca pozitia unor detalii se obtine direct pe fotografii speciale, metrice, numite fotograme, executate in anumite conditii, fie din avion (denumite fotograme aeriene) fie de la nivelul solului (fotograme terestre). Ca si topografia, exploatarea fotogramelor se face utilizand reteua de sprijin creata cu ajutorul geodeziei.

Prin produsele pe care le furnizeaza - harti si planuri - masuratorile terestre sunt indispensabile diverselor domenii de activitate, indiferent de stadiul de executie al unei lucrari; sunt folosite la constructia si sistematizarea teritoriala, la organizarea teritoriului agricol, la amenajarea silvica sau hidrologica, in prospectarea si exploatarea zacamintelor de substante utile, precum si la elaborarea de studii si cercetari in domeniul hidrografic, pedologic, geologic, geografic.

Importanta stiintifica a masuratorilor terestre consta in aceea ca furnizeaza date necesare studierii formei si dimensiunilor reale ale Pamantului si modificarile in timp ale acestora.

Elementele topografice ale terenului.

Forma si dimensiunile Pamantului.

Sectionarea cu un plan vertical a scoartei terestre permite observatia ca se disting trei curbe care o intereseaza si anume : suprafata topografica, geoidul si elipsoidul de referinta (figura 1.1). Suprafata topografica este de fapt urma terenului lasata pe planul de sectiune, urma care, datorita neregularitatilor, nu se poate exprima printr-un model matematic. Este suprafata care face obiectul reprezentarilor pe harti si planuri.

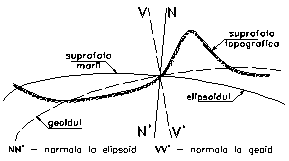
Figura - Suprafata topografica, geoidul si elipsoidul de referinta.

Geoidul reprezinta locul geometric al punctelor care materializeaza nivelul marilor si oceanelor linistite, nivel neafectat de miscarea valurilor, curentilor sau mareelor, prelungit pe sub continente. Numit si suprafata de nivel zero, nu se poate exprima printr-un model sau formula matematica. Datorita faptului ca nu reprezinta nici macar aproximativ configuratia terenului natural, nu face obiectul reprezentarii pe harti si planuri, fiind de fapt o forma geometrica ipotetica din punct de vedere al exprimarii.

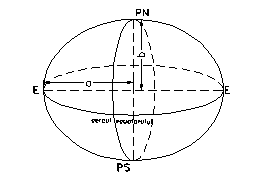
Figura - Elipsoidul de referinta.

Elipsoidul de referinta (figura 1.2) a aparut ca urmare a imposibilitatii reprezentarii terenului sau a geoidului pe harti si planuri prin coordonate. Fiind descris de o relatie matematica, corespondenta reciproca intre puncte din teren si omoloagele lor pe elipsoid permite raportarea acestora pe harti si planuri prin coordonate, intr-un sistem unic si unitar. In timp, s-au folosit o serie de elipsoizi de referinta care au purtat numele celor care le-au descris prin marimile lor caracteristice: Delambre, Bessel, Heyford, Krasovski. Pentru toate tipurile de elipsoizi cunoscuti, elementele caracteristice cu valorile acestora numai pentru elipsoidul Krasovski,sunt:

a = 6378245 m (semiaxa mare)

b = 6356863 m (semiaxa mica)

a = (a-b)/a = 1/298 (turtirea elipsei)

Proiectia punctelor in geodezie si topografie.

Elementul care defineste modalitatea de proiectare a punctelor pe o suprafata este marimea acesteia in sensul ca la suprafetele mari se impune sa se tina cont de curbura Pamantului (cazul unor regiuni, tari, continente sau intreg globul), in timp ce daca suprafata determinata de puncte este mica, influenta curburii se poate neglija.

In primul caz avem de-a face cu ceea ce se numeste proiectie geodezica iar in al doilea caz cu o proiectie topografica a punctelor.

Prin proiectia geodezica a punctelor de triangulatie A, B, C, D pe suprafata elipsoidului, in punctele a, b, c, d se obtin triunghiuri cu laturi curbe, laturi care se numesc si linii geodezice. Se poate observa (figura 1.3) ca in acest caz proiectantele punctelor de triangulatie sunt convergente catre o zona din centrul globului pamantesc. Daca suprafata pe elipsoid este mica (cazul punctelor apropiate), putem asimila elipsoidul cu o suprafata plana fara ca precizia coordonatelor si pozitia punctelor sa sufere.

In acest caz proiectantele punctelor vor fi paralele intre ele, iar pozitia punctelor de triangulatie se defineste prin coordonatele rectangulare plane x, y precum si prin cota H, reprezentand distanta pe verticala de la suprafata de nivel zero la punctul din teren.

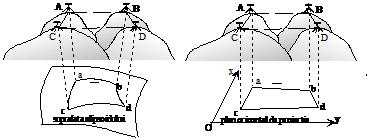
Figura - Proiectia geodezica si proiectia topografica a punctelor.

Se poate observa ca totdeauna distantele care se pot determina pe planuri reprezinta, de fapt, proiectii orizontale ale distantelor inclinate corespondente, din teren. Deasemeni, aceste distante sunt liniile drepte care unesc punctele din teren, indiferent de configuratia terenului in lungul acestui traseu.

Proiectii cartografice.

Deoarece in cazul general se impune reprezentarea grafica a unor suprafete intinse ale globului, se constata existenta a doua dificultati mari:

suprafata globului este curba, apropiata de o sfera;

reprezentarea reliefului ar trebui sa fie tridimensionala.

Aceste dificultati se pot elimina prin alegerea unui numar suficient de puncte caracteristice, proces numit si geometrizarea terenului, dupa care suprafetele curbe se transforma, prin calcule, in suprafete plane. O astfel de transformare nu se poate face insa fara ca distantele de pe elipsoid sa nu sufere modificari. Functie de sistemul de proiectie adoptat se pot modifica si alte elemente cum sunt unghiurile sau suprafetele. Clasificarea proiectiilor cartografice se va face deci functie de elementele care se pastreaza nemodificate, astfel:

conforme sunt cele care pastreaza unghiurile nedeformate;

echivalente sunt cele care pastreaza suprafetele nedeformate;

echidistante sunt cele care pastreaza numai anumite distante nedeformate;

arbitrare sunt cele care nu pastreaza nici un element nedeformat.

Din cele prezentate, putem constata ca deformatiile pot fi liniare, unghiulare sau areolare (deformarea suprafetelor). Un alt criteriu de clasificare al proiectiilor cartografice este cel al modului de realizare a reprezentarii, care conduce la aspectul retelei cartografice; in acest caz clasificarea se prezinta astfel:

azimutale sunt proiectiile in care reprezentarea se face pe un plan tangent sau secant la sfera in punctul central al zonei de reprezentat;

cilindrice sunt cele in care reprezentarea se face pe un cilindru care are o pozitie oarecare fata de sfera (nu este obligatoriu sa fie tangent).

conice sunt cele la care reprezentarea se face pe un con tangent sau secant la sfera, cu variantelor cunoscute ca proiectiile policonice si cele pseudoconice.

Din prima categorie face parte proiectia stereografica, care, pentru teritoriul Romaniei a fost aplicata si cunoscuta initial ca 'proiectia stereografica 1933' si mai recent 'proiectia stereografica 1970'; pozitia punctului central in cele doua proiectii difera in sensul ca prima avea acest punct in zona Brasov pentru ca a doua sa-l aiba in zona Fagaras. In figura 1.4 sunt ilustrate elementele ce caracterizeaza o proiectie stereografica:

C centrul de proiectie,

V punctul de vedere,

R₀ raza medie de curbura la centrul de proiectie,

CD adancimea planului de proiectie,

M - un punct pe elipsoid,

m - proiectia pe planul secant a punctului M,

r - raza cercului de secanta

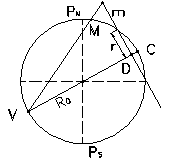
Figura - Proiectia stereografica.

Din a doua categorie, pentru tara noastra a fost folosita 'proiectia Gauss'. Pentru a obtine aceasta proiectie, este suficient sa se introduca o sfera intr-un cilindru pentru ca apoi sfera sa fie rotita cu unghiuri egale (figura 1.5). "Feliile" din sfera sunt proiectate pe cilindru, una langa alta si apoi cilindrul este taiat pe generatoarele ce trec prin cei doi poli. Fata vizibila se aseaza in plan, obtinand o reprezentare in proiectia Gauss.

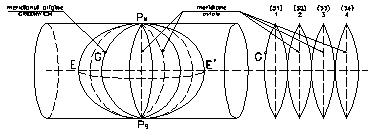
Figura - Proiectia Gauss.

Reprezentarea elipsoidului se face in acest caz prin zone denumite fuse avand in general 6 pe longitudine. Meridianul origine, numit si 'meridian 0', este cel care trece prin Observatorul Greenwich. Avantajele acestei proiectii constau in aceea ca permite reprezentarea intregului glob pe zone cuprinse intre cei doi poli.

Dezavantajele se refera la situatia teritoriilor relativ mici care se reprezinta uneori pe doua fuse vecine (cazul tarii noastre in L - 34 si L - 35), precum si la faptul ca deformatiile sunt uneori mai mari decat in alte proiectii.

Elementele topografice ale terenului.

In mediul inconjurator se afla o serie de obiecte naturale ( vai, dealuri, ape, munti) si artificiale, aparute datorita omului (constructii, limite intre folosinte sau proprietati), toate alcatuind detalii topografice.

Pentru determinarea formei si pozitiei acestora, se aleg, pe detaliul din teren, puncte caracteristice denumite topografice, reprezentand schimbari de directie ale unui contur sau a pantei terenului, sau minimum de puncte in functie de care sa se poata reprezenta orice detaliu sau forma de teren (figura 1.6). La stabilirea minimului de puncte este necesar sa se cunoasca scara planului sau a hartii.

Detaliile topografice sunt, in general, alcatuite din linii sinuoase a caror determinare si exprimare matematica ar fi practic imposibila si apoi chiar si inutila. Aceeasi linie sinuoasa se poate transforma intr-o linie franta care sa imbrace si sa inlocuiasca cu suficienta fidelitate conturul initial. In figura 1.6 sunt prezentate doua moduri de a geometriza un contur sinuos : in cazul 'a', datorita faptului ca s-au ales putine puncte pe contur, geometrizarea este incorecta, in timp ce in cazul 'b', datorita numarului adecvat de puncte alese, linia franta care aproximeaza conturul sinuos este mult mai aproape ca forma de acest contur.

Figura - Geometrizarea terenului

Operatiunea poarta denumirea de geometrizarea terenului si se poate face atat in plan orizontal, cand un punct se determina prin coordonate x si y, cat si in plan vertical, situatie in care determinarea se face prin cota si distanta fata de un reper ales.

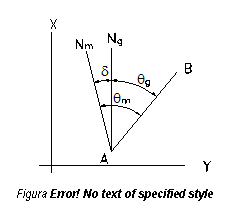
Doua sunt categoriile de elemente care se masoara in teren si anume cele liniare respectiv unghiulare. Intersectia suprafetei topografice cu un plan vertical ce trece prin punctele M si N se numeste aliniament, fiind o linie sinuoasa in plan vertical, in timp ce in plan orizontal este o linie dreapta.

Materializarea unui aliniament intre doua puncte si reprezentarea lui intr-o sectiune verticala (figura 1.7) conduce la definirea urmatoarelor elemente topografice ale terenului:

distanta inclinata, L, intre punctele A si B, este lungimea liniei drepte intre punctele marcate in teren; ea este linia geometrizata intre punctele A si B din teren.

distanta orizontala, D, reprezinta proiectia in plan orizontal a distantei inclinate L.

unghiul de panta a este unghiul format de orizontala ce trece printr-un punct si directia catre cel de-al doilea punct (figura 1.7). Unghiurile de panta, la fel ca si diferenta de nivel, pot fi pozitive sau negative. Pozitive sunt unghiurile de panta catre toate punctele situate deasupra liniei orizontului, dupa cum unghiurile de panta sunt negative pentru toate punctele situate sub linia orizontului. Daca directia de referinta nu este orizontala ce trece printr-un punct ci verticala locului, atunci unghiul format de verticala cu directia MN se numeste unghi zenital si se noteaza cu 'Z'. Intre unghiul zenital si unghiul de panta al unei directii date exista totdeauna relatia:

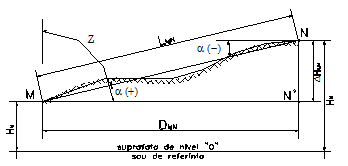
Figura - Elementele topografice ale terenului.

diferenta de nivel DH_MN = H_N - H_M, este distanta pe verticala intre planele orizontale ce trec prin punctele M si N. Din figura 1.7 se observa ca diferenta de nivel poate fi pozitiva (de la M la N) sau negativa (de la N la M). Marimea diferentei de nivel intre punctele M si N se poate calcula, functie de lungimea inclinata L si unghiul de panta a, cu relatia :

sau, daca se cunoaste marimea unghiului zenital, Z:

cota unui punct se defineste ca distanta pe verticala de la suprafata de referinta la planul orizontal ce trece prin acel punct. Din figura 1.7, se poate deduce cota punctului N, H_N, functie de cota punctului M, H_M, presupusa ca fiind cunoscuta si diferenta de nivel DH_MN, calculata cu una din relatiile [1.2] sau [1.3], functie de elementele masurate.

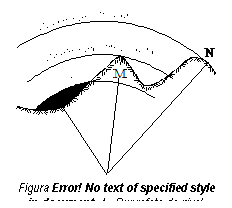
unghiul orizontal b (figura 1.8), intre directiile MN si MP este unghiul diedru format de planele verticale ce contin punctele M si N (planul V_N), respectiv M si P (planul V_P). Marimea lui se obtine din diferenta directiilor catre punctele P si N, putand avea valori cuprinse intre 0^g si 400^g.

Figura - Unghiul orizontal intre doua aliniamente.

orientarea directiei MN, q_MN, se defineste ca unghiul format de directia nordului cu directia de masurat (MN), unghi masurat in sensul orar. Orientarea unei directii se calculeaza din coordonatele punctelor ce determina directia, cu relatii de tipul :

[1.4]

pozitia unui punct in plan se defineste fie prin coordonatele rectangulare x si y, fie prin coordonatele polare. Coordonatele punctului M din figura 1.8 se calculeaza functie de coordonatele punctului N cu relatiile:

[1.5]

Unitati de masura.

Functie de elementele care se determina in operatiile topografice, in tara noastra se folosesc unitatile de masura ale sistemului international si anume:

pentru lungimi, metrul cu multipli si submultipli sai;

pentru suprafete, unitatile ce deriva din cele folosite la lungimi, metrul patrat, kilometrul patrat; se mai folosesc insa si arul,respectiv hectarul, astfel:

10 m * 10 m = 100 mp = 1 a (un ar)

100 m * 100 m = 10000 mp = 100 a = 1 ha (un hectar)

pentru unghiuri, gradele si radianii. Datorita dificultatilor de exprimare in sistemul zecimal, gradatia sexagesimala a fost inlocuita cu gradatia centesimala. Astfel, un cerc are 400 grade centesimale, (notate 400 ^g ), iar un cadran 100^g. Submultipli sunt minutul centesimal, egal cu 1/100 dintr-un grad (notat 1^c ), respectiv secunda sexagesimala, egala cu 1/100 dintr-un minut ( notata 1^cc ). Pentru transformari dintr-un sistem in altul, se folosesc urmatoarele relatii:

din sexagesimal in centesimal : 1 = 1,111111^g

din centesimal in sexagesimal : 1^g = 0,9

Radianul este unghiul caruia i se opune un arc egal cu raza cercului pe care-l descrie. Legatura intre radian si unitatile de masura in grade este:

sexagesimal r '' = 206265 ''

centesimal r^cc = 636620^cc

Suprafete de referinta si sisteme de coordonate.

Suprafete de referinta.

Determinarea in plan vertical a pozitiei punctelor se face prin raportare la geoid, caz in care suprafata se numeste suprafata de nivel zero. Pozitia acesteia se obtine prin observatii multianuale. Aparatele cu care se determina cota marii sau oceanului se numesc medimaregrafe sau medimaremetre. Ele constituie punctele fundamentale pentru originea cotelor in lucrarile de masuratori terestre.

Suprafata care este normala in fiecare punct al ei la directia verticalei se numeste suprafata de nivel. Altitudinea sau cota absoluta a punctului topografic se defineste ca fiind distanta pe verticala intre suprafata de nivel zero si suprafata de nivel ce trece prin punctul considerat.

In cazul suprafetelor mari se poate considera ca Pamantul este aproximativ sferic, iar suprafetele de nivel, inclusiv suprafata de nivel zero sunt sfere concentrice in centrul Pamantului (figura 1.9). Pentru suprafete mici, se considera ca suprafetele de nivel, inclusiv cea de nivel zero, sunt plane paralele si orizontale intre ele.

Pentru anumite lucrari desfasurate pe suprafete mici si precis definite, este posibil ca suprafata de nivel, considerata originea in determinarea cotelor, sa fie alta decat suprafata de nivel zero, aleasa conventional.

In acest caz spunem ca avem de-a face cu o altitudine conventionala a punctului. In acest caz, cotele tuturor punctelor de pe aceasta suprafata, vor diferi fata de cotele absolute cu aceeasi cantitate, egala cu distanta pe verticala intre suprafata de nivel zero si suprafata conventional aleasa. In aceste conditii, relieful terenului este reprezentat pe harti sau planuri identic, indiferent de sistemul de referinta ales pentru cote (absolut sau conventional).

Sisteme de coordonate.

Pentru a cunoaste directiile cardinale ale hartilor si planurilor, acestea trebuie sa fie orientate. Acest lucru inseamna ca directiile identificate pe o harta sau plan sa fie facute paralele cu omoloagele lor din teren, prin rotirea in mod convenabil a hartii sau planului.

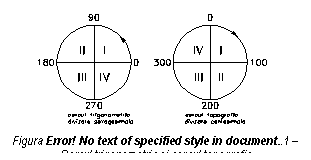
Directia care se foloseste in orientarea lucrarilor de masuratori terestre, numita directie de referinta, este directia nordului geografic. Tinand cont de faptul ca determinarile se fac in sens orar, pentru a se pastra relatiile cunoscute din trigonometrie, s-a adoptat cercul topografic, la care numerotarea cadranelor se face in sens orar, pornind de la directia nordului (figura 1.10).

Deoarece exista nordul geografic (stabil in timp) si nordul magnetic (variabil in timp indelungat), rezulta ca si orientarile pot fi geografice (fixe in timp) respectiv magnetice (usor variabile in timp).

Prin orice punct de pe suprafata terestra pot fi duse un meridian geografic si unul magnetic; implicit, o directie oarecare, intr-un sistem de axe de coordonate este orientata fata de o paralela la meridianul axial si nu fata de meridianul geografic al locului respectiv. Considerand o directie A-B in teren (figura 1.11), fata de aceasta se disting urmatoarele orientari:

orientarea magnetica (sau azimutul magnetic), care este unghiul format de directia nordului magnetic cu directia A-B;

orientarea geografica (sau azimutul geografic) care este unghiul format de directia nordului

geografic cu directia A-B;

Unghiul format de cele doua orientari poarta denumirea de deviatie magnetica d. Acest unghi este necesar in cazul determinarii orientarilor cu busola, in vederea corectarii acestora pentru a se putea raporta la orientari geografice.

Notiuni de teoria erorilor de masurare.

Avand in vedere ca orice masuratoare, oricat de precis ar fi executata, este insotita de mici diferente fata de valoarea reala a marimii respective, vom defini erorile ca fiind micile diferente care apar la masurarea repetata a unei marimi. Este de mentionat ca valoarea reala a marimii masurate nu este niciodata cunoscuta. Cauzele care conduc la aparitia erorilor se refera la:

imperfectiunilor constructive ale aparaturii sau dispozitivelor cu care se executa masuratorile, erorile numindu-se erori instrumentale;

datorita operatorului care executa masuratorile, caz in care erorile se numesc erori personale;

datorita conditiilor de mediu in care se efectueaza masuratorile, situatie in care erorile se numesc erori datorate conditiilor exterioare;

Este de remarcat ca niciodata, categoriile enumerate mai sus nu actioneaza singure, ci apar toate la un loc. Eroarea se defineste matematic ca diferenta intre valoarea eronata si valoarea justa, iar corectia este totdeauna diferenta intre valoarea justa si valoarea eronata. Daca notam cu v_j valoarea justa si cu v_e valoarea eronata, putem scrie ca:

[1.12]

dupa cum :

[1.13]

Din expresiile [1.12] si [1.13] se poate scrie ca :

[1.14]

Daca asupra unei marimi se vor face un numar mare de determinari, se vor calcula abaterile fiecarei determinari fata de media aritmetica si se va intocmi un grafic pe care se vor raporta, pe abscisa marimea erorilor, iar pe ordonata frecventa aparitiei unei valori a erorii, se va obtine un grafic al unei curbe, cunoscuta sub numele de 'curba clopot GAUSS', reprezentand de fapt curba de distributie normala a erorilor intamplatoare.

Clasificarea erorilor se poate face dupa:

marimea lor:

erori propriu-zise, care sunt acceptate in procesele de masurare;

erori grosolane, numite si greseli, care nu se accepta in sirul de masuratori, motiv pentru care, la prelucrare, sunt eliminate.

modul de propagare:

sistematice, caracterizate prin aceea ca sunt constante ca semn si marime. Acest tip de erori nu se pot elimina, dar influenta lor poate fi anulata prin calcul;

intamplatoare sau accidentale, apar aleator ca semn si valoare, iar influenta lor nu se cunoaste si nu se poate diminua.

valoarea de referinta:

reale, care reprezinta diferentele intre diversele valori din sirul de determinari si valoarea reala a marimii masurate. Se poate lesne constata ca deoarece valoarea reala a marimii nu este cunoscuta, nici erorile reale nu se pot determina.

aparente, care reprezinta diferenta intre fiecare valoare din sirul de masuratori si valoarea cea mai probabila, definita ca media aritmetica a celor 'n' determinari.

In cazul unui numar de determinari facute asupra aceleasi marimi, de un singur operator, cu un singur instrument de masura si in conditii meteo aproximativ identice, suma erorilor aparente tinde la 0. Daca vom nota cu "v" erorilor aparente, cu M_i masuratorile propriu-zise si cu M media celor 'n" determinari, putem scrie:

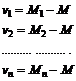[1.15]

Prin insumarea relatiilor [1.15], se ajunge la egalitatea:

[1.16]

Daca notam suma erorilor v_i cu [v] si suma masuratorilor cu [M], relatia [1.16] se poate scrie sub forma:

[1.17]

si deci:

[1.18]

care constitue criteriul de apreciere a corectitudinii prelucrarii masuratorilor.

Pornind de la considerentul ca un sir de masuratori este reprezentat ca o functie de cele 'n' determinari, asimilate ca 'n' variabile, erorile sunt derivatele de ordinul I in raport de aceste determinari. Diferenta intre oricare doua masuratori din sirul de masuratori efectuate se numeste ecart; daca aceasta diferenta se face intre valoarile extreme, se numeste ecart maxim.

Pentru a putea fi prelucrat, sirul determinarilor trebuie sa se incadreze in toleranta "T", care se defineste ca fiind ecartul admisibil intre masuratori. Valoarea tolerantei se precizeaza prin instructiuni tehnice si valoarea ei este obligatoriu de respectat in orice gen de lucrari de masuratori terestre. Tehnica care se ocupa cu modul de prelucrare a masuratorilor si ajungerea la valoarea cea mai probabila se numeste teoria erorilor de masurare, iar procedeul se numeste al celor mai mici patrate.

Dupa modul in care se obtin, marimile masurate pot fi:

directe, caracterizate prin aceea ca observatiile sunt facute direct cu instrumentul asupra marimii care se masoara, de exemplu, masurarea unei distante cu ajutorul ruletei;

indirecte, in care, prin calcul, din marimi determinate direct se obtin marimile care intereseaza. Un exemplu este determinarea a doua laturi intr-un triunghi in care se cunosc toate unghiurile si a treia latura.

conditionate, in care marimile masurate direct trebuie sa raspunda unor conditii, ca de exemplu, suma unghiurile masurate intr-un triunghi sa fie egala cu 200^g.

Din punct de vedere al modului de efectuare a observatiilor sau al aparaturii folosite, se disting:

masuratori de aceeasi precizie, numite si masuratori de ponderi egale, in care determinarile se fac cu aceeasi metoda, de un singur operator care foloseste un singur tip de aparat;

masuratori de precizii diferite, numite si masuratori ponderate, care se efectueaza cu aparate diferite, de catre operatori diferiti, in conditii si cu instrumente diferite.

Eroarea medie patratica individuala.

Pornind de la forma generala a ecuatiilor de erori, si anume:

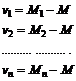[1.19]

pentru a se inlatura incertitudinile datorate semnelor + si - ale erorilor v_i, se ridica la patrat suma erorilor si prin insumare se ajunge la eroarea medie patratica individuala:

[1.20]

Aceasta eroare constituie un criteriu de apreciere calitativa a sirului de masuratori luate individual. Asupra valorii erorii medii patratice individuale actioneaza preponderent erorile intamplatoare cu valoare absoluta mare, tocmai cele care determina gradul de siguranta al masuratorilor. Datorita faptului ca aceasta eroare este relativ stabila, este practic suficient un numar relativ mic de determinari pentru a obtine aceasta eroare cu o precizie satisfacatoare.

Eroarea medie a mediei aritmetice.

Pornind de la 'i' masuratori efectuate in aceleasi conditii asupra unei singure marimi M, valoarea cea mai probabila se accepta a fi media aritmetica. Se poate deci scrie ca:

[1.21]

sau:

[1.22]

Daca acceptam ca fiecare masuratoare este afectata de aceeasi eroare, e_q, in timp ce eroarea medie patratica a valorii M va fi e_M, prin ridicare la patrat si neglijand termenii de ordinul II (adica produsele intre termenii 'i' si 'j'), atunci putem scrie ca :

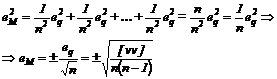[1.23]

acesta marime este un criteriu de apreciere a preciziei masuratorilor.