| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
DETERMINAREA PUNCTULUI NAVEI CU OBSERVATII ASTRONOMICE
1 TEORIA DREPTEI DE INALTIME
Dreapta de inaltime este linia de pozitie astronomica determinata de inaltimea observata la un astru.
Determinarea punctului navei prin calcularea simultana a latitudinii si longitudinii consta in determinarea pozitiei zenitului observatorului pe sfera cereasca astfel (fig.1):
φ = δZ
λ = PZ

Pozitia astrului de coordonate ecuatoriale PGrA, δA proiectata pe sfera terestra se numeste punct subastral de coordonate φa, λa rezultand:
φa = δA
λa = PGrA
astfel ca pozitia punctului subastral al oricarui astru poate fi determinat din coordonatele ecuatoriale ale astrului (pentru stele unghiul la pol la Greenwich se determina din relatia T = Ts + τ).
Cercul de egala inaltime sau cercul de inaltime cu centrul in punctul subastral si de raza sferica egala cu distanta zenitala a astrului, este cercul de pe suprafata Pamantului de pe care un astru se vede sub aceeasi inaltime, fiind determinat de linia de pozitie de pe sfera cereasca numita cerc de egala distanta zenitala.
Cu inaltimea masurata la un astru de inaltime h se determina pozitia punctului subastral folosind coordonatele ecuatoriale ale astrului si se traseaza cercul de inaltime de raza z = 90s - h. Cu alte cuvinte observatorul se va afla pe acest cerc de inaltime si, deci pentru determinarea punctului acestuia este nevoie de doua linii de pozitie intersectarea a doua cercuri de inaltime). Deoarece pe harta marina aceste linii de pozitie astronomice apar sub forma unor curbe complicate si raza unui cerc de inaltime are valori foarte mari (de ordinul miilor de mile marine) ele sunt inlocuite cu segmente foarte mici de arc de inaltime reprezentate sub forma unei drepte tangente la arcul de inaltime intr-un punct numit punct determinativ k si poarta numele de dreapta de inaltime (fig.2).

Fig. 2
2 CONSTRUCTIA SI TRASAREA DREPTEI DE INALTIME PE HARTA
Punctul determinativ K se obtine la intersectia arcului de cerc mare ce contine punctul estimat al navei φe, λe cu arcul de inaltime observata la astru, perpendiculare intre ele astfel ca dreapta de inaltime se traseaza ca o perpendiculara pe directia punctului estimat - punctul subastral.
Pozitia punctului determinativ este determinata de relevmentul adevarat al punctului subastral (azimutul astrului, unghiul Pn, punctul estimat, punctul subastral) si de marimea segmentului punctului estimat - punctul determinativ.
Pozitia punctului determinativ (fig.3) se afla din diferenta dintre distanta zenitala estimata he si distanta zenitala adevarata ha iar segmentul punct estimat punct determinativ este diferenta de inaltime Δh:
Δh = ha - he (2.14)

unde: K' este proiectia pe sfera cereasca a punctului determinativ K.
Dreapta de inaltime se traseaza pe harta marina folosind:
azimutul astrului;
diferenta de inaltime.
Algoritm (fig.4):
se determina punctul estimat al navei;
prin punctul estimat se traseaza azimutul astrului Az
(relevmentul adevarat la punctul astral);
se masoara pe azimut diferenta de inaltime Δh in minute
de arc de cerc mare (mile marine) catre astru daca Δh
este pozitiv si in directia opusa astrului, daca Δh este
negativ si se obtine punctul determinativ K;
se traseaza dreapta de inaltime prin punctul determinativ
sub forma unui perpendiculare pe azimut.

Fig. 4
3 CALCULUL ELEMENTELOR PENTRU TRASAREA DREPTEI DE INALTIME
Elementele folosite pentru trasarea dreptei de inaltime se determina astfel:
a) diferenta de inaltime:
- se masoara cu sextantul inaltimea la astru si se corecteaza:
hi + ε = ha
se calculeaza inaltimea estimata la astru rezolvand
triunghiul sferic de pozitie:
![]()
b) azimutul astrului:
se calculeaza rezolvand triunghiul sferic de pozitie cu:
![]()
Unghiul la zenit are valori de la 0s la 180s de la N spre est sau vest pentru latitudini nordice si de la S spre est la vest pentru latitudini sudice.
Unghiul la zenit se transforma in azimut astfel:
a)- in emisfera nordica:
pentru PE Az = z
pentru PW Az = 360s - z
b)- in emisfera sudica
pentru PE Az = 180s - z
pentru PW Az = 180s + z
sau cu : ![]()
Cadranul de orizont in care se afla astrul se afla:
a) - daca φ si δ sunt de semne contrare:
astrul in cadranul SE pentru PE;
astrul in cadranul SW pentru PW.
b)- daca δ > si de acelasi semn:
astrul in cadranul NE pentru PE;
astrul in cadranul NW pentru PW.
c)- daca δ < φ si de acelasi semn :
- Pc - originea de cotare a unghiului la pol poate fi N sau S, functie de raportul dintre inaltimile sau unghiurile la pol din momentul observatiei he si P si valorile pentru momentul trecerii astrului prin punctul vertical h1 si P1:
astrul in cadranul NE pentru PE>P1 sau he>h1
astrul in cadranul SE pentru PE<P1 sau he>h1;
astrul in cadranul NW pentru PW>P1 sau he<h1;
astrul in cadranul SW pentru PW<P1 sau he>h1;
Observatie: valorile P1 si h1 se scot din tablele nautice.
Unghiul la zenit cuadrantal se transforma in azimut astfel:
Az = z, pentru astrul in cadranul NE;
Az = 180s - z, pentru astrul in cadranul SE;
Az = 180s + z pentru astrul in cadranul SW;
Az = 360s - z, pentru astrul in cadranul NW.
4 DETERMINAREA PUNCTULUI NAVEI CU OBSERVATII SIMULTANE LA ASTRII
Punctul navei cu observatii simultane la astrii se determina pe timpul noptii folosind doua-trei linii de pozitie prin masurarea cvasimultan inaltimea la 2-3 astri (pe timp de zi numai in conditii deosebite cand se vad Soarele, Luna, planeta Venus sau Steaua Sirius).
Conditiile pentru determinarea cu precizie a punctului cu observatii simultane la astri sunt urmatoarele:
- diferenta dintre azimuturile astrilor sa fie apropiata de 120s (90s pentru observatii la doi astri) ce asigura o intersectie favorabila a liniilor de pozitie;
- inaltimea astrilor sa fie intre 30s si 70s, deoarece valoarea inaltimilor prea mici este influentata mult de refractia atmosferica, iar inaltimile prea mari provoaca erori in trasarea dreptei de inaltime.
Algoritm:
se aleg astrii convenabili pentru momentul observatiei;
se determina starea absoluta a cronometrului;
se face controlul si reglarea sextantului, se determina
eroarea indicelui sextantului;
se masoara rapid serii de 3 la 5 inaltimi la fiecare astru,
si se noteaza ora cronometrului pentru fiecare observatie;
se determina punctul estimat si se scot coordonatele
estimate pentru momentul mediu al celei de a doua
observatii;
se calculeaza inaltimile medii si ora cronometrului
pentru fiecare serie de observatii;
se calculeaza elementele dreptelor de inaltime Az si Δh;
se va face reducerea primei inaltimi la zenitul celei de a
doua inaltimi);
se traseaza dreptele de inaltime si se obtine punctul
astronomic (observat, φa, λa);
se determina grafic eroarea in punct ca valoare de
relevment adevarat si distanta de la punctul estimat la cel
observat, se noteaza O/Cl;
se trec in jurnal informatiile referitoare la determinarea
punctului astronomic.
Observatie: reducerea inaltimii primului astru observat pentru zenitul celei de a doua observatii se face prin adunarea corectiei Δhm obtinuta din:
![]()
adica aceasta corectie reprezinta variatia inaltimii astrului datorita intervalului de timp dintre observatii cand nava a parcurs spatiul m, astfel ca se traseaza:
Az1 (Δh1 + Δhm);
Az2, Δh2.
Dreptele de inaltime se traseaza direct pe harta sau utilizand scara grafica, astfel:
- se construieste scara longitudinilor si a latitudinilor:
se traseaza scara longitudinii, un segment orizontal de dreapta se imparte in segmente de 5 sau 10 mm (lungimea unui minut de longitudine);
in originea acestei drepte se construieste unghiul egal cu valoarea latitudinii punctului estimat si se obtine scara latitudinii;
se marcheaza minutele de latitudine ridicand perpendiculare de pe scara longitudinilor;
se traseaza dreptele de inaltime si la intersectia lor se duce punctul observat;
se scot cu compasul pe verticala si pe orizontala diferentele dintre punctul observat si cel estimat si se raporteaza la scara latitudinilor si cea a longitudinilor si se obtin diferentele Δφ si Δλ;
se determina punctul adevarat:
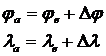

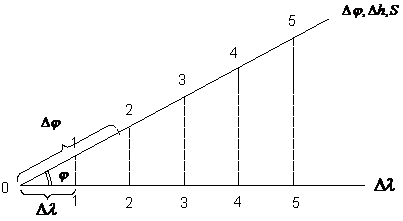
5 DETERMINAREA PUNCTULUI NAVEI CU TREI OBSERVATII SIMULTANE LA ASTRI AFECTATE DE EROARE
In determinarea punctului navei cu trei observatii simultane la astri apar adeseori erori reprezentate prin intersectia celor trei linii de pozitie, nu intr-un punct, ci sub forma unui triunghi, numit triunghiul erorilor.
Daca laturile acestui triunghi sunt mai mici de 2 mile marine se apreciaza ca fiind acceptabila pozitia navei, eroarea de pozitionare aparand ca urmare a erorilor accidentale si punctul probabil se considera centrul triunghiului erorilor.
Cand laturile triunghiului erorilor sunt mai mari de 2 mile marine se considera ca triunghiul erorilor a aparut ca rezultat al erorilor sistematice in determinarea liniilor de pozitie astronomice si trebuie sa se elimine influenta acestor erori prin diferite procedee.
5.1 Procedeul triunghiurilor asemenea cand diferenta de azimut este de aproximativ 120s (fig.6)
Algoritm:
dupa obtinerea triunghiului erorilor se modifica diferentele de inaltime cu 2' - 4' si se obtin noile diferente de inaltime: Δh'1, Δh'2, Δh'3;
se traseaza noile drepte de inaltime ale caror elemente sunt Az1, Δh'1, Az2, Δh'2, Az3, Δh'3 si se obtine un triunghi asemenea triunghiului erorilor, mai mic sau mai mare;
se unesc varfurile de acelasi nume ale triunghiurilor si la intersectia acestora se obtine punctul observat al navei, intotdeauna in interiorul triunghiului erorilor.
5.2 Procedeul triunghiurilor asemenea cand diferenta este de aproximativ 60s
Algoritm: este identic cu cel prezentat anterior cu diferenta ca intersectia dreptelor care unesc varfurile celor doua triunghiuri asemenea se face in afara triunghiului erorilor (fig.7).


Fig. 7
6 DETERMINAREA PUNCTULUI NAVEI CU OBSERVATII SUCCESIVE LA SOARE
Pe timp de zi punctul navei astronomic se determina cu observatii succesive la Soare, facute la intervale de timp determinate care sa asigure variatia azimutului la Soare cu cel putin 30s (asigurandu-se o intersectie favorabila a acelor drepte de inaltime, din care una va fi transportata pentru momentul celei de a doua observatii la Soare) (fig.8).
Observatiile se pot face pentru o inaltime oarecare a Soarelui si pentru inaltimea meridiana sau pentru doua inaltimi oarecare ale Soarelui.
Algoritm:
se determina punctul estimat al navei, se efectueaza
prima observatie la Soare, se noteaza O1/Cl1;
dupa un interval de timp ales astfel incat azimutul
Soarelui s-a modificat cu cel putin 30s se executa a doua
observatie la Soare; se noteaza O2/Cl2; se calculeaza
elementele celei de a doua drepte de inaltime;
se traseaza cele doua linii de pozitie din care prima este
transportata la nivelul celei de a doua observatii, si la
intersectia lor se obtine punctul estimat observat al
navei;
se determina grafic eroarea in punct si se inscriu in jurnal
informatiile referitoare la determinarea punctului.
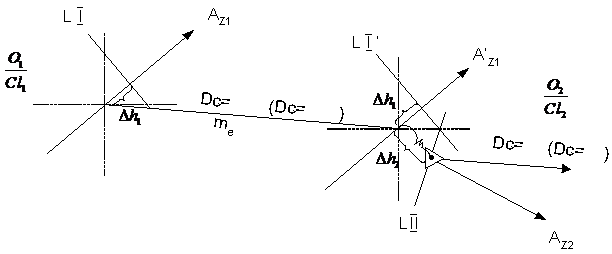
Fig.8
7 PREGATIREA OBSERVATIILOR ASTRONOMICE. UTILIZAREA NAVISFEREI
Navisfera este un instrument de navigatie utilizat pentru:
pregatirea observatiilor de seara si de dimineata;
identificarea astrilor;
determinarea orei rasaritului si apusului astrilor.
Navisfera reprezinta, la scara mica, proiectia sferei ceresti pe un glob stelar cuprinzand stele de la marimea 1 la marimea 4, si ecliptica.
Navisfera se compune din:
sfera cereasca pe care sunt raportate stelele cele mai importante pentru navigatie; sunt trasate ecuatorul ceresc, ecliptica, meridianele si paralele ceresti;
cercul meridianului observatorului in interiorul caruia se roteste sfera cereasca in jurul unui ax prin polii ceresti;
cercul azimutal ce reprezinta orizontul adevarat al observatorului;
cercul de inaltime;
indicatorul special pentru indicarea precisa a astrului ce se poate atasa la nevoie pe semicercul inaltimilor;
cutia navisferei.
Raportarea soarelui, lunii si a astrilor pe navisfera se face astfel:
se scoate din efemerida declinatia astrului si timpul solar, lunar planetar si timpul sideral;
se calculeaza ascensiunea dreapta:
a Ts - Ta (soare, luna, planete)
se aseza sfera astfel incat ecuatorul ceresc sa coincida cu planul cercul azimutal;
se roteste sfera pana ce gradatia de pe ecuator ce corespunde ascensiuni drepte ajunge in dreptul cercului meridianului observatorului;
se raporteaza cu creionul pe navisfera un punct in dreptul gradatiei de pe meridianul observatorului, corespunzatoare declinatiei astrului;
Orientarea navisferei reprezinta miscarea acestuia in asa fel incat partea de deasupra planului orizontului reprezinta emisfera vizibila la un moment dat. Orientarea navisferei se face astfel:
se orienteaza navisfera dupa latitudine; se roteste cercul meridianului observatorului pana ce in dreptul pozitiei N, sau S, functie de latitudine, de pe cercul azimutal ajunge gradatia corespunzatoare colatitudinii(90 j); miscarea diurna se obtine prin miscarea navisferei de la E la V;
se orienteaza navisfera dupa timpul
sideral al locului calculat(![]() ): se roteste apoi globulstelar in jurul axului polilor
ceresti(fara a modifica orientarea dupa latitudine
pana ce gradatia de pe ecuator, corespunzatoare meridianului ajunge in dreptul cercului
meridianului observatorului ).
): se roteste apoi globulstelar in jurul axului polilor
ceresti(fara a modifica orientarea dupa latitudine
pana ce gradatia de pe ecuator, corespunzatoare meridianului ajunge in dreptul cercului
meridianului observatorului ).
7.1 Utilizarea navisferei in navigatia astronomica
Pregatirea observatiilor cu ajutorul navisferei
Pregatirea observatiilor reprezinta procesul prin care se aleg astrii la care se fac observatii pentru determinarea punctului navei
Algoritm:
se calculeaza ora sfarsitului crepusculului civil tf pentru observatiile de seara sau ora inceputului crepusculului nautic pentru observatiile de dimineata;
se calculeaza timp sideral ts pentru aceasta;
se orienteaza navisfera dupa latitudinea punctului estimat pentru momentul observatiilor si dupa timpul sideral
se orienteaza un semicerc al inaltimii in dreptul unei stele convenabila observatiei si se citesc inaltimea si azimutul stelei; se noteaza ora, steaua aleasa inaltimea si azimutul acesteia;
se repeta aceasta operatiune pentru a se alege stele cu diferenta de azimut de aproximativ 90 , aproximativ 60 sau 120
Identificarea astrilor cu ajutorul navisferei
Algoritm:
se masoara inaltimea la astru si un relevment compas la aceasta si se converteste in Ra (Az);
se orienteaza dupa latitudine si timpul sideral;
se aduce unul din cercurile de inaltime in dreptul gradatiei corespunzatoare unghiului la zenitul cuadrantal de pe cercul azimutal, dupa care in dreptul gradatiei de pe semicercul inaltimilor corespunzatoare inaltimii masurate se gaseste astrul.
Determinarea orei si azimutul rasaritului si apusului astrului
Algoritm:
se orienteaza navisfera dupa latitudine;
se roteste navisfera dupa axa lumii pana ce astrul ales vine pe orizont in emisfera estica, pentru rasarit sau in cea vestica pentru apusul astrului si se citeste timpul sideral al locului pe ecuatorul ceresc in dreptul arcului meridianului observatorului si se transforma in ora bordului, se citeste si azimutul pe cercul azimutal.
Determinarea orei culminatiei stelelor
Algoritm:
se orienteaza navisfera dupa latitudine;
se roteste navisfera dupa axa lumii pana ce steaua aleasa vine in dreptul meridianului observatorului si se citeste timpul sideral al locului pe ecuatorul ceresc in dreptul cercului meridianului observatorului si se transforma in ora bordului; se citeste si inaltimea meridianului a stelei pe meridianul observatorului in dreptul acesteia.
8 ASTRII UTILIZATI IN NAVIGATIA MARITIMA
Cunoasterea astrilor reprezinta conditia fundamentala pentru determinarea punctului navei cu observatii astronomice.
Astrii utilizati in navigatia maritima sunt:
Soarele, Luna;
Planetele: Venus, Marte, Jupiter si Saturn;
Stelele.
Planetele se identifica dupa miscarea lor aparenta printre stele, in apropierea eclipticii, si dupa conturul regulat in forma de disc.
planeta Venus numita si Luceafarul de seara sau de dimineata este cel mai stralucitor astru de pe cer, ce poate fi vazut si pe timp de zi cu ochiul liber;
planeta Jupiter este de o stralucire apropiata de cea a stelei Sirius, uneori mai luminoasa si de o culoare alb-argintie;
planeta Marte este recunoscuta dupa culoarea sa rosiatica;
planeta Saturn se recunoaste dupa culoarea sa alb-galbuie.
Efemeridele nautice contin informatii locale despre pozitiile si conditiile de observare ale planetelor.
Cerul unei nopti clare si fara luna ofera posibilitatea observarii vizuale a unui numar de peste 2500 de stele din miliardele de galaxii si de stele ce formeaza universul cunoscut.
Pentru observatiile astronomice nautice se folosesc insa un numar relativ mic de stele bine cunoscute si usor de identificat prin aliniamente imaginare ce le leaga pe bolta cereasca.
Stelele utilizate in navigatia astronomica fac parte dintr-o serie de constelatii importante:
Carul Mare (Ursa Major) constelatie cunoscuta inca din antichitate si care este constituita din sapte stele: a-Dubhe, b-Merak, g-Phecda, d-Megrez, (rotile carului), e-Alioth, x-Mizar, h-Alkaid sau Benetnash ( oistea carului) si este folosita ca reper pentru identificarea celorlalte stele folosite in navigatie in emisfera nordica.
Constelatia este recunoscuta dupa forma caracteristica si intensitatea luminoasa a stelelor ce o compun.
2) Carul Mic (Ursa Minor) este cea mai importanta constelatie deoarece contine Steaua Polara, ce se afla foarte aproape de Polul Nord ceresc; constelatia este formata din 7 stele printre care: a-Polaris sau Alruccahab, b-Kochab, g-Pherkad, d-Yildun
Constelatia este dificil de recunoscut datorita slabei luminozitati ale stelelor principale dar compenseaza prin recunoasterea usoara a Stelei Polare si a stelei Kochab
(aflata la extremitatea constelatiei, opusa Stelei Polare); Steaua Polara se gaseste pe aliniamentul format din stelele Merak si Dubhe din Carul Mare la o departare de 5 ori distanta dintre acestea doua.
3) Cassiopeia este constelatia usor de recunoscut prin forma sa specifica in forma de W sau M; este importanta deoarece este pozitionata intre Steaua Polara si Andromeda; este vizibila tot anul de pe latitudini medii nordice; stelele principale din Casiopeia sunt: a-Schedar sau Shedir, b-Caph, g-Navi, d-Ruchbah.
4) Orion se recunoaste prin forma de trapez delimitat de patru stele foarte luminoase si de "centura lui Orion" formata din trei stele mai putin luminoase; principalele stele dim Orion sunt: a-Betelgeuse, b- Rigel, g-Bellatrix, d-Mintaka, e-Alnilam, x-Alnitak, h-Saiph, q-Meissa.
Orion se afla "cu centura" sa aproximativ pe ecuatorul ceresc, la jumatatea aliniamentului format intre Aldebaran (a Tauri) si Sirius (a Canis Major).
5) Cainele Mare (Canis Major) aflat in apropierea lui Orion, este recunoscut prin steaua sa principala a Sirius, situata pe aliniamentul Aldebaran (a Tauri) - "centura" lui Orion, opusa lui Aldebaran.
Principalele stele din Cainele Mare sunt: a-Sirius, b-Mirzam sau Murzim, g-Muliphein, d-Wezen.
6) Lebada (Cygnus) cu steaua principala Deneb, are o forma caracteristica de cruce ("crucea nordului") si care face parte din "triunghiul marinarilor" cu stelele Altair (a Aquilae) si Vega (a Lyrae).
Principalele stele din Lebada sunt: a-Deneb, b-Albireo, g- Sadr, e-Gienah.
) Gemenii (Gemini) cu stelele Castor si Pollux, aflata pe aliniamentul stelelor diagonale Betelgeuse si Rigel din Orion sau cu steaua Pollux pe aliniamentul format de Megrez si Merak din Carul Mare.
Principalele stele din Gemeni sunt: a-Castor, b-Pollux, g-Alhena,sau Almeisan, d- Wasat sau Wesat, e-Mebsuta, x-Mekbuda, h- Propus sau Tejat.
8) Cainele Mic (Canis Minor) este constelatia aflata intre Gemenii si Cainele Mare pe aliniamentul Bellatrix - Betelgeuse din Orion, cu steaua principala Procyon.
9) Taurul (Taurus) este constelatia situata pe aliniamentul Saiph - Bellatrix din Orion, iar steaua sa principala Aldebaran pe aliniamentul "centurii " lui Orion.
Stelele importante din Taurul sunt: a-Aldebaran, b-El Nath , g -HyadumI, d-Hyadum II.
10) Coroana Boreala ( Corona Borealis) este constelatia caracterizata de forma de coroana a stelelor sale si se afla pe aliniamentul Arcturus (a Bootis) si Vega (a Lyrae).
Stelele importante din Coroana Boreala sunt: a-Alphecca sau Gemma si b-Nasukan.
11) Leul (Leo) este constelatia aflata pe aliniamentul Dubhe - Merak din Carul Mare opus Stelei Polare.
Principalele stele din Leul sunt: a-Regulus, b-Denebola, g-Algeiba, d-Duhr,e-Algenusi, x-Adhafera, h-Alterf.
12) Vizitiul (Auriga) este constelatia aflata la est de Perseu, steaua Capella gasindu-se pe aliniamentul facut de stelele Alkaid si Mizar din Carul Mare in directia stelei Aldebaran din Taurul.
13) Lira (Lyra) este constelatia aflata in partea dreapta a bazei facuta de constelatia Lebada iar steaua Vega se afla pe aliniamentul Capella-Steaua - Polara. Stelele principale din Lira sunt : a-Vega, b-Sheliak, g-Sulafat.
14) Vulturul (Aquila) este constelatia situata la sud de Lebada, iar steaua Altair se afla pe aliniamentul Capella - constelatia Cassiopeia; stelele principale din Vulturul sunt: a-Altair, b-Alshain, g-Tarazed, x-Deneb el Okab ("coada vulturului').
15) Bootes se recunoaste prin prezenta stelei Arcturus, neconfundabila prin marime si luminozitate si este situata intre Coroana Boreala si Carul Mare; stelele principale sunt: a-Arcturus, b-Nakkar, g-Saginus, e-Pulcherimma, h-Muphrid.
16) Pegasus este constelatia recunoscuta dupa forma de patrat, format de trei din stelele sale si steaua Alpheratz din Andromeda, aflata in partea opusa Carului Mare pe aliniamentul Merak - Dubhe; stelele principale din Pegasus sunt: a-Markab, g-Algenib, d-Alpheratz sau Sirah, b-Scheat, x-Homan, e-Enif, h-Matar.
17) Andromeda este constelatia aflata intre Perseu si Pegasus cu stelele:
a-Alpheratz, b-Mirach, g-Almak.
18) Perseu ( Perseus) este constelatia aflata pe aliniamentul Phecda - Dubhe din Carul Mare si Mirach - Almak din Andromeda; stelele principale sunt: a-Mirfak sau Algenib, b- Algol, x-Menkhib.
19) Sagetatorul (Sagittarius) este constelatia de la est de Scorpionul, in apropierea "cozii" acestuia; stelele principale sunt ; a-Rukbat, b b Arkab, Urkab, g-Al Nasl, d-Kaus Medix, e-Kaus Australis, l-Kaus Borealis, x-Ascella, s-Nuaki.
20) Scorpionul (Scorpius) este constelatia aflata langa Sagetator, cu stelele principale : a-Antares, b Graffias sau Akrab, d-Dschubba, l-Shaula.
21) Pestii (Pisces) este constelatia aflata pe aliniamentul Steaua Polara si Scheat - Markab din Pegasus, spre sud.
In emisfera sudica principalele constelatii si stele folosite pentru observatii sunt: Crucea Sudului (Crux) si stelele Achernar a Eriadnus, Canopus a Carina, constelatia Centaurul (Centaurus) langa Crucea Sudului cu stelele Rigil Kent si Hadar.
9 EFEMERIDA NAUTICA. CONTINUT. DESCRIEREA TABLELOR ZILNICE. CALCULUL UNGHIULUI LA POL SI DECLINATIEI SOARELUI, LUNII, PLANETELOR SI STELELOR
9.1GENERALITATI
Pentru rezolvarea problemelor de astronomie nautica este necesara cunoasterea coordonatelor ecuatoriale ale astrilor la care s-au executat observatii. Documentul nautic in care se dau coordonatele ecuatoriale ale astrilor precum si alte date referitoare la astri, necesare determinarii punctului navei si altor activitati de la bord se numeste efemerida nautica.
Tarile cu traditie in calculul si editarea efemeridelor nautice sunt: Marea Britanie - Brown's Nautical Almanac (B.N.A.), Rusia - Morskoi Astronomiceskii Ejegodnik (M.A.E.), Franta - Ephemerides Nautiques, Italia - Effemeridi Nautiche, Statele Unite - The Nautical Almanac etc.
Relatiile de calcul pentru rezolvarea problemelor sunt aceleasi, diferind doar notatiile si simbolurile de la un tip de efemerida la alta.
9.2 EFEMERIDA BROWN'S NAUTICAL ALMANAC (B.N.A.)
Almanahul BNA se compune din sapte parti mari, completate cu: reclame, informatii despre tehnica de navigatie, posibilitati de aprovizionare si reparatii, titlurile documentelor si manualelor noi aparute.
I. Notiuni preliminare:
- introducere;
- calendarul pentru anul in curs si pentru anul urmator;
- sarbatorile legale si aniversarile din Marea Britanie;
- eclipsele de Soare si Luna pentru anul in curs (al efemeridei);
- informatii asupra timpului - ora de vara;
- inceputul astronomic al anotimpurilor;
- informatii asupra mareei inalte pe Tamisa si inundatiile probabile;
- explicatia simbolurilor astronomice folosite;
- fazele Lunii pentru anul in curs;
- table de corectii pentru inaltimile masurate la astri;
- tabla de conversie a marimilor de timp in marimi de arc si invers;
- tabla de conversie a marimilor circulare in marimi cuadrantale si invers.
II. Partea I - efemerida nautica:
- explicatii privind utilizarea efemeridei nautice;
- informatii despre planete pe anul in curs;
- table astronomice zilnice;
- table de interpolari si corectii;
- table cu unghiul sideral t si declinatia d stelelor;
- table de corectii pentru determinarea latitudinii din inaltimea stelei Polare si azimutul stelei Polare;
- informatii pentru identificarea stelelor principale.
III. Partea a II-a - table astronomice si nautice:
- table de conversie a timpului, vitezei si distantei;
- table de latitudine si azimut - metoda;
- table de determinare a distantei in functie de viteza si timp;
- table de determinare a vitezei in functie de distanta si timp;
- table pentru determinarea distantelor prin diferente de drum si doua relevmente masurate la un interval de timp;
- table de curent - deriva de curent si drumul deasupra fundului;
- table de determinare a timpului in functie de distanta si viteza.
IV. Partea a III-a - table de maree:
- table de maree - predictiile zilnice pentru coastele Marii Britanii, vestului Europei, India, Australia, Noua Zeelanda, Canada si America.
- tabla cu timpul standard folosit in predictiile zilnice de maree;
- table cu constantele de maree pentru porturile britanice;
- table cu constantele de maree pentru porturile straine;
- informatii despre curentii de maree din jurul insulelor britanice si Marea Nordului;
- informatii despre maree;
- timpul standard - pentru statele lumii;
- table pentru determinarea inaltimii mareei la un moment dat, intre apa inalta si apa joasa;
- table pentru determinarea distantei cu sextantul.
V. Partea a IV-a - drumuri si distante
- table de drumuri si distante in jurul insulelor
britanice, in Marea Nordului si Canalul Englez;
- informatii despre pilotaj.
VI. Partea a V-a - ghid despre farurile, geamandurile si balizele din apele britanice:
- informatii despre faruri, semnale de ceata, semnale de pericol si noul sistem de balizaj;
- abreviatiile folosite in lista farurilor;
- faruri, geamanduri si balize in apele Marii Britanii, Irlandei si in Canal;
- faruri, geamanduri si balize straine, de la raul Elba la Brest:
coasta Germaniei, Olandei, Belgiei si Frantei.
VII. Partea a VI-a - distante intre porturi:
- distantele de la porturile britanice la principalele porturi straine;
- distantele de la porturile Statelor Unite si Canadei la porturile principale ale lumii;
- table de distante intre porturile din diferite zone ale lumii.
VIII. Partea a VII-a - informatii diferite:
- table de conversii:
- metrii in picioare si inchi si invers;
- inchi in milimetri si invers;
- metri cubi in picioare cubice si invers;
- tone metrice pe centimetru imersiune in tone pe inch imersiune si invers;
- tone lungi in tone metrice si tone scurte si invers;
- greutatea specifica a apei in porturile lumii;
- table de salinitate a apei de mare;
- informatii despre incarcare - indici de stivuire;
- linia de schimbare a datei;
- reglementari in vigoare;
- regulamentul international pentru prevenirea coliziunilor pe mare COLREG;
- abreviatii utilizate in shipping si comert maritim;
- informatii despre compensarea compasului magnetic;
- generalitati privind comunicatiile radio in navigatie;
- utilizarea radarului in navigatia maritima;
- platformele maritime de extractie a gazului si petrolului din Marea Nordului;
- meteorologie maritima;
- radiogoniometrarea - principii;
- facilitatile radiotelefonului maritim international VHF;
- radiobalizele din apele Marii Britanii;
- vocabularul standard de navigatie maritima;
- informatii privind mijloacele de salvare si utilizarea lor;
- semnale de pericol;
- sistemul de navigatie Omega;
- navigatia satelitara;
- functii trigonometrice;
- dictionar de nume si termeni din astronomie;
- alfabetul fonetic;
- definitii si termeni utilizati in electrotehnica;
- generalitati despre girocompas;
- informatii generale despre salvare si cautare;
- alte informatii utile la bord.
Notatii si simboluri:
G.M.T. = timp mediu la Greenwich Tm;
G.H.A. = timp la Greenwich T;
S.H.A. = unghiul sideral t
ARIES = punctul vernal g
Dec. = declinatia astrului d
v = variatia orara a timpului la Greenwich;
d = diferenta orara a declinatiei;
Mer.Pass. = ora culminatiei;
S.D. = semidiametrul;
H.P. = paralaxa orizontala;
Lat. = latitudinea geogrefica j
Twilight = crepuscul;
Sunrise = rasaritul Soarelui;
Moonrise = rasaritul Lunii;
Sunset = apusul Soarelui;
Moonset = apusul Lunii;
Eqn. of Time = ecuatia timpului Em;
Upper = superioara;
Lower = inferioara;
Age = varsta Lunii;
Phase = faza Lunii;
L.H.A. ARIES = timpul sideral al locului (ts);
![]() = astru nu rasare
(circumpolar invizibil);
= astru nu rasare
(circumpolar invizibil);
![]() = astru nu apune
(circumpolar vizibil);
= astru nu apune
(circumpolar vizibil);
/ / / = zi crepusculara.
9.3 CALCULUL UNGHIULUI LA POL SI DECLINATIEI ASTRILOR
Tablele zilnice ale efemeridelor nautice contin unghiul orar la Greenwich T si declinatia d a astrilor sistemului solar in functie de data si timp mediu la Greenwich Tm din ora in ora.
Citirea coordonatelor din tabla zilnica se face functie de Tm, la precizie de ore intregi, imediat inferior momentului observatiei. Corectiile DT si Dd pentru diferenta de timp mediu la Greenwich DTm fata de momentul observatiei se determina cu tablele de interpolari si corectii.
Timpul mediu la Greenwich pentru momentul observatiei Tm este :
Tm = A + (Tm - A)
Data la Greenwich pentru momentul observatiei:
- daca 0h < Tm < 24h data este aceeasi cu data locului;
daca Tm > 24h se scad 24h din Tm si se adauga o zi la data locului;
daca Tm < 0h se aduna 24h la Tm si se scade o zi la data locului.
Unghiul orar al astrului: t = T + l care se transforma in unghi la pol:
- daca t <180 atunci PW = t;
- daca t > 180 atunci PE = 360 - t.
Calculul unghiului la pol si declinatiei se executa la precizie de 0'.1 .
a) Calculul unghiului la pol si declinatiei Soarelui.
Data Ptr.Tm = .h Ta = . d = . (d=
Var. ptr. DTm = .m.s + DTa = . + Dd
Pentru Tm = .h.m.s Ta = . d = .
+ l
ta = .
P = .
unde :
- DTm reprezinta diferenta dintre Tm pentru momentul observatiei si cel imediat inferior pentru care s-a intrat in tabla, ca ora intreaga;
- DTa reprezinta crestere unghiului orar la Greenwich al Soarelui, corespunzator DTm si se obtine din tabla de interpolari si corectii;
- d reprezinta variatia orara a declinatiei Soarelui din ziua observatiei si se citeste in partea de jos a coloanei stabilindu-se semnul acesteia prin compararea a doua marimi consecutive ale declinatiei, corespunzatoare Tm imediat inferior si imediat superior Tm corespunzator momentului observatiei;
- Dd reprezinta corectia declinatiei Soarelui functie de DTm si d si se obtine din tablele de interpolari si corectii pe coloana "Corr".
b) Calculul unghiului la pol si declinatiei Lunii (si planetelor)
Data Ptr.Tm = .h T (♂) = . (v= d =. (d=
Var. ptr. DTm = .m.s + D T (♂) = .
Var. ptr. DTm, v si d + D T (♂) = . + Dd
Pentru. Tm = .h.m.s T (♂) = . d
+ l
t (♂) = .
P = .
unde :
- D T (♂) reprezinta crestere unghiului orar la Greenwich al Lunii (planetei Marte), corespunzator DTm si se obtine din tabla de interpolari si corectii;
- D T (♂) reprezinta corectia suplimentara a unghiului orar la Greenwich ce se obtine din tablele de interpolari si corectii functie de DTm si v, pe coloana "Corr";
v reprezinta diferenta dintre variatia unghiului orar la Greenwich si variatia orara folosita in calculul tablelor de interpolari (Luna - 14 19'0, planete - 15
c) Calculul unghiului la pol si declinatiei stelelor
Data ptr.Tm = .h Ts = .
Var. ptr. DTm = .m.s + DTs = .
Pentru. Tm = .h.m.s Ts = .
l = .
ts = .
d t
t* = .
P = .
unde :
- DTs reprezinta crestere timpului siderat la Greenwich
corespunzator DTm si se obtine din tabla de interpolari si corectii;
d si t reprezinta coordonatele ecuatoriale ale stelei la data observatiei.
9.4 TIPURI DE CALCUL UTILIZATE IN NAVIGATIA ASTRONOMICA
a) Observatii la Soare (Luna, planete):
Date necesare : data, ora, Cl, Ze(j l), A, (Tm - A)V, k, hi, e, i.
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul P si d Soarelui (Lunii, planetei)
Data ptr. Tm = . T = . (v = .) d = . (d = .)
Var. ptr. DTm = . +D T = .
Cu DTm, v si d +D T = . + Dd
Pentru Tm = . T = . d
+ l
t = .
PW = t daca t < 180 sau
PE = 360 - t daca t > 180
4. Calculul he si Az
sin he = sin j sin d + cos j cos d cos P = a + b; sin Ze = sec he cos d sin P
j = . log sin j = . log cos j = . log sec he = .
d = . + log sin d = . + log cos d = . + log cos d = .
P = . + log cosP = . + log sin P = .
log a = . log b = . log sin Zc = .
a = . b = . Zc = .
+ b = . Az = .
sin he = . sau cu Tablele ABC :
he = . A = .
+ B = .
C = . Zc = .
5. Calculul ha_ 6. Calculul Dh
hi = . ha = .
+ e - he = .
ho = . Dh = .
+ cor. tot. = .
+ cor. supl. = .
ha = . Linia de pozitie ( Az = . ; Dh = . )
b) Observatii la stele :
Date necesare : data, ora, cl, Ze(j l), A, (Tm - A)V, k, hi, e, i.
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul P* si d
Data ptr. Tm = . Ts = .
Var. ptr. DTm = . + DTs = .
Pentru Tm = . Ts = .
+ l
ts = .
d t
t* = .
PW = t daca t < 180 sau
PE = 360 - t daca t > 180
4. Calculul he si Az sin he = sin j sin d + cos j cos d cos P = a + b; sin Ze = sec he cos d sin P
j = . log sin j= . log cos j = . log sec he =
d = . + log sin d = . + log cos d = . + log cos d
P = . + log cos P = . + log sin P = .
log a = . log b = . log sin Zc = .
a = . b = . Zc = .
+ b = . Az = .
sin he = . sau cu tablele ABC :
he = . A = .
+ B = .
C = . Zc = .
5. Calculul ha_ 6. Calculul Dh
hi = . ha = .
+ e - he = .
ho = . Dh = .
+ cor. tot. = .
ha = Linia de pozitie ( Az = . ; Dh = . )
Reducerea inaltimilor la acelasi zenit
Date necesare : A1 (2, ., n), Az1 (2, ., n), Dh1 (2, ., n)
1. Calculul Dt 2. Calculul m
An = . m = Vn Dt / 6
- A1 (2, ., n - 1) = . Vn / 6 = .
Dt1 (2, ., n - 1) = . Dt = .
m(cab) = .
m(M) = .
Calcul RpA 4. Calculul Dhz Az = . Dhz = m cos RpA cu T.32(DH-90) :
- Da = . m = . sau RpA = .
RpA = . cos RpA = . Vn = .
( semicircular ) Dhz = . Dh/min = .
Dhz = Dt Dh / min
Dt = .
Dh / min = .
Dhz = .
5. Calculul Dhr
Dh = .
Dhz = .
Dhr = .
a) La zenitul ultimei observatii :
Semnul lui "Dhz" este dat de "m" (+) si "cos RpA" (+ sau -), adica :
pozitiv (+) - daca RpA < 90
negativ (-) - daca RpA > 90
b) La zenitul primei observatii :
Semnul lui "Dhz" este dat de "m" (-) si "cos RpA" (+ sau -), adica :
pozitiv (+) - daca RpA > 90
negativ (-) - daca RpA < 90
Calculul separat al latitudinii
a) Observatii la Soare (Luna)
i) Meridiana:
Date necesare : data, ora, cl, Ze(j l), Hi, e, i.
1. Calculul orei culminatiei si d Soarelui (Lunii)
Data Culm. Soarelui (Lunii) la merid. Greenwich Tm = tm = .
Corectia ptr. l = . si Dt = .
- l
d = . ( d = . ) Tm = .
Dd + lf
d = . tf = .
Pentru ora de vara Df
2. Calculul Ha Calculul ja
+ e - Ha = ....
+ cor. tot. = . + d
+ cor. supl. = . ja
Ha = .
ii) Circummeridiana
Date necesare : data, ora, Cl, Ze(j l), A, (Tm - A)V, k, hi, e, i.
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul P si d Soarelui (Lunii, planetei)
Data ptr. Tm = . T = . (v = .) d = . (d = .)
Var. ptr. DTm = . +D T = .
Cu DTm, v si d +D T = . + Dd
Pentru Tm = . T = . d
+ l
t = .
PW = t daca t < 180 sau
PE = 360 - t daca t > 180
4. Calculul unghiului la pol limita Plim
Cu j si d (din T.35 DH-90) Plim = .
P ( (h) = .
Daca P < Plim observatia este in limitele circummeridiane
5. Calculul coeficientului k _ 6. Calculul reductiei r 100 tg j = . (din T.33a DH-90) cor I = .(din T.33b DH-90)
- 100 tg d = . (din T.33a DH-90) + cor II = . (din T.33c DH-90)
k = . r = .
7. Calculul Ha_ 8. Calculul ja
+ e - Ha = ....
+ cor. tot. = . + d
+ cor. supl. = . ja
ha = .
+ r = .
b) Observatii la Steaua Polara
Date necesare : data, ora, cl, Ze(j l), A, (Tm - A)V, k, hi, e, i.
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul ts _ 4. Calculul ha
Var. ptr. DTm = . + DTs = . + e
Pentru Tm = . Ts = . ho = .
+ l + cor. tot. = .
ts = . ha = .
5. Calculul corectiei speciale 6. Calculul ja
cor. I = . ha = .
+ cor. II = . + cor. SP. = .
+ cor. III = . ja
cor. SP. = .
c) Observatii oarecare la Soare
Date necesare: data, ora, Cl, A, (Tm - A)V, k, ha, emisfera observatorului.
NOTA : Se poate utiliza orice astru a carui declinatie d nu este nula.
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm _
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul P si d Soarelui _
Data ptr. Tm = . Ta = . (v = .) d = . (d = .)
Var. ptr. DTm = . +D Ta = .
Cu DTm, v si d +D Ta = . + Dd
Pentru Tm = . Ta = . d
+ l
ta = .
PW = ta daca ta < 180 sau
PE = 360 - ta daca ta > 180
4. Calculul unghiului auxiliar X 5. Calculul unghiului auxiliar Y
tg X = ctg d cos P sin V = sin ha cos X cosec d
- log ctg d = . log sin ha = .
+ log cos P = . + log cos X = .
log tg X = . + log cosec d
X = . log sin Y = .
Y = .
6. Calculul ja
jN - ( Y + X ) sau jS = Y - X
Y = ...... Y = .
+ X = ...... - X = .
- ( Y + X ) = ...... jS
jN
Calculul separat al longitudinii
a) Observatii la Soare (Luna, planete)
Date necesare : data, ora, Cl, Ze(j l), A, (Tm - A)V, k, hi, e, i, Ra.
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm _
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul T si d Soarelui (Lunii, planetei) _
Data ptr. Tm = . T = . (v = .) d = . (d = .)
Var. ptr. DTm = . +D T = .
Cu DTm, v si d +D T = . + Dd
Pentru Tm = . T = . d
4. Calculul ha_
hi = .
+ e
ho = .
+ cor. tot. = .
+ cor. supl. = .
ha = .
5. Calculul P si t _
log sin ha = .
+ log sec j = . log tg j
+ log sec d = . + log tg d
log m = . log n = .
m = . n = .
+ n = .
cos P = .
P = . daca Ra > 180 P = PW
daca Ra < 180 P = PE
t = PW sau t = 360 - PE
6. Calculul la _
t = . T = .
- T = . - t = .
lE lW
b) Observatii la stele
Date necesare : data, ora, cl, Ze(j l), A, (Tm - A)V, k, hi, e, i, Ra.
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm _
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul T* si d
Data ptr. Tm = . Ts = .
Var. ptr. DTm = . + DTs = .
Pentru Tm = . Ts = .
d t
T* = .
4. Calculul ha
hi = .
+ e
ho = .
+ cor. tot. = .
ha = .
5. Calculul P* si t* _
log sin ha = .
+ log sec j = . log tg j
+ log sec d = . + log tg d
log m = . log n = .
m = . n = .
+ n = .
cos P = .
P = . daca Ra > 180 P = PW
daca Ra < 180 P = PE
t* = PW sau t* = 360 - PE
6. Calculul la _
t* = . T* = .
- T* = . - t* = .
lE lW
Calculul ja si la pentru momentul culminatiei soarelui
a) Algoritm de aplicare
1. Masurarea inaltimilor circummeridiane (inainte si dupa momentul culminatiei) si inaltimii maxime (H).
2. Reprezentarea variatiei inaltimii functie de timp si determinarea momentului corespunzator inaltimii maxime (AH).
NOTA: Daca dupa culminatie se pot observa inaltimi exact de aceeasi valoare cu cele masurate anterior culminatiei, momentul culminatiei se poate determina analitic astfel:
AH = ( A1 + A4 ) / 2 = ( A2 + A3 ) / 2
sau
AH = ( A1 + A2 + A3 + A4 ) / 4
Calculul unghiului la Greenwich al Soarelui (Ta) pentru momentul culminatiei determinat grafic sau analitic.
Calculul longitudinii pentru momentul culminatiei (acceptand ca unghiul orar al locului este zero) cu relatia: lE = ta - Ta sau lW = Ta - ta .
5. Calculul latitudinii pentru momentul culminatiei cu relatia :
ja - Ha ) d
b) Tipuri de calcul
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm _
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul Ta _
Data ptr. Tm = . Ta = . (v = .)
Var. ptr. DTm = . +D Ta = .
Cu DTm, v si d +D Ta = . _
Pentru Tm = . Ta = .
Ta( = ( Tm( ) + Em(
sau
Ta(h) = ( Tm(h) 12h ) + Em(h)
4. Calculul la
ta = 359
- Ta = ......
lE
daca lE < 180 lE lE
daca lE > 180 lW lE
5. Calculul Ha_ 6. Calculul ja
+ e - Ha = ....
+ cor. tot. = . + d
+ cor. supl. = . ja
Calcule pentru determinarea corectiei compasului
a) Cu Soarele (Luna) la rasarit (apus) :
Date necesare : data, ora, cl, Ze (j l), Rc (Rg), dm (Ag).
1. Calculul orei rasaritului (apusului) Soarelui (Lunii) _
Data Ora ras (apus) O ( ) la Gr. ptr. j = . Tm = tm = .
Corectia ptr. Dj = . si D t = . = .
Corectia ptr. l = . si D t = . = .
Ora rasaritului (apusului) in punctul estimat tm = .
- l(h)
Ora ras. (apus) la merid. locului exprim. in Tm Tm = .
+ lf
tf = .
Pentru ora oficiala de vara + Df
Ora bordului (legala) = .
2. Calculul d Soarelui (Lunii) _
Data ptr. Tm = . d = . (d = .)
Pentru Tm = . d
Calculul Az in momentul rasaritului (apusului) _
Din T.40 (DH-76) cu j si d Ampl. = .
Ampl. bord sup. = .
Az. bord sup. = .
sau:
Din T.37a,b (DH-90) cu j si d Zs = . Az = .
4. Calculul Dc (Dg) 5. Calculul dm (Ag)
- Rc (Rg) = . - dm (Ag) = .
Dc (Dg) = . dm dg
b) Cu Steaua Polara:
Date necesare : data, ora, cl, Ze (j l), Rc (Rg), dm (Ag).
1. Calculul ts _
ora bordului = .
lf
Tm = .
Data ptr. Tm = . Ts = .
Var. ptr. DTm = . + DTs = .
Pentru Tm = . Ts = .
+ l
ts = .
2. Calculul Az Stelei Polare _
Din efemerida (Azimutul Stelei Polare) ts si
latitudinea estimata Zs = NE (NW) .
360
Az = .....
Calculul Dc (Dg) 4. Calculul dm (Ag)
Az = . Dc (Dg) = .
- Rc (Rg) = . - dm (Ag) = .
Dc (Dg) = . dm dg
c) Cu un astru la o inaltime oarecare :
Date necesare : data, ora, cl, Ze(j l), A, (Tm - A)V, k, Rc(Rg), dm(Ag).
1. Actualizarea starii absolute a cronometrului 2. Calculul Tm _
(Tm - A)V = . A = .
+ k n/24 = . + (Tm - A)act = .
(Tm - A)act = . Tm = .
Calculul P si d astrului _
Data ptr. Tm = . T = . (v = .) d = . (d = .)
Var. ptr. DTm = . +D T = .
Cu DTm, v si d +D T = . + Dd
Pentru Tm = . T = . d
+ l
t = .
PW = t daca t < 180 sau
PE = 360 - t daca t > 180
4. Calculul Az _
log tg d
+ log cos j = . log sin j
+ log cosec P = . + log ctg P = .
log m = . log n = .
m = . n = .
+ n = .
ctg Zc = .
Zc = . Az = .
Observatie: Daca ctg Zc rezulta pozitiv, Zc se masoara de la polul ridicat spre est sau spre vest dupa cum indica unghiul la pol P. Daca ctg rezulta negativ, Zc se masoara de la polul coborat spre est sau spre vest corespunzator unghiului la pol P.
Az = Zc(NE) = 180 - Zc(SE) = 180 + Zc(SW) = 360 - Zc(NW)
5. Calculul Dc (Dg) 6. Calculul dm (Ag)
Az = . Dc (Dg) = .
- Rc (Rg) = . - dm (Ag) = .
Dc (Dg) = . dm dg
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3939
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved