| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Elemente de baza ale calculului neuronal
Cercetarile actuale in domeniul calculului neuronal sunt motivate de dorinta de a construi retele neuronale artificiale. Desi, dupa cum si numele de retele neuronale o implica, la inceput scopul a fost modelarea matematica a retelelor neuronale biologice, astazi gama aplicabilitatii lor este aproape universala.
Din punct de vedere neurofiziologic, modelele construite cu ajutorul retelelor neuronale artificiale sunt extrem de simplificate, ele au totusi suficiente trasaturi care surprind cele mai importante trasaturi ale "calculului" biologic.
1. Neuronul biologic.
Unitatea celulara fundamentala a sistemului nervos, si in particular a creierului este neuronul. Creierul uman este constituit din aproximativ 1011 neuroni, fiecare neuron fiind interconectat cu aproximativ 104 alti neuroni. In Fig.2.1. este reprezentat schematic un neuron biologic.
Neuronul biologic este constituit din trei parti fundamentale [62]:
a). Arborele dendritic care colecteaza semnalele de intrare de la alti neuroni.
b). Soma care transforma in anumite conditii semnalele de intrare in semnale de iesire.
c). Axonul care transmite semnalul de iesire catre alti neuroni prin intermediul arborelui axonic.
Neuronii sunt interconectati prin intermediul unor legaturi numite sinapse, care reprezinta punctele de contact dintre ramurile arborelui axonic ale unui neuron pre-sinaptic si ramurile arborelui dentritic ale unui neuron post-sinaptic.
Neuronii comunica intre ei prin intermediul unor semnale electrice, nu-mite potentiale de actiune sau impulsuri, care sunt propagate de-a lungul axonului, prin pastrarea amplitudinii si formei semnalului electric, pana cand intalnesc legatura sinaptica. La sinapsa o substanta chimica, numita neuro-transmitator, este stocata intr-un numar mare de vezicule. Potentialul de actiune elibereaza continutul anumitor vezicule catre clestele sinaptic.
Moleculele neuro - transmitatorului ajung la membrana neuronului post-sinaptic, unde receptia acestor molecule induc un potential de actiune post-sinaptic (PSP).
PSP-urile generate in diferite puncte ale arborelui dendritic difuzeaza prin atenuare catre soma, unde ele sunt integrate. Daca suma totala a PSP-urilor integrate in limita unui scurt interval de timp depaseste un anumit prag (threshold) de aproximativ cateva zecimi de minivolti, numit nivel de activare, neuronul va deveni activ, generand un potential de actiune de-a lungul axonului.
|
|
Fig. 2.1. Reprezentarea schematica a neuronului biologic.
1 - Arborele dendritic; 2 - Soma (corpul celular); 3 - Nucleul celulei neuronale; 4 - Axonul; 5 - Arborele axonic; 6 - Conexiuni sinaptice;
Contributia unui semnal de intrare la PSP caracterizeaza marimea numita tarie sinaptica sau eficienta sinaptica. Un astfel de semnal de intrare are o valoare de aproximativ 1 minivolt, putand fi un semnal excitator sau un semnal inhibitor, in functie de influenta pozitiva sau negativa pe care o are in a face un neuron ca sa devina activ. Trebuie sa subliniem faptul ca PSP-ul nu este unic determinat de semnalul de intrare. Diferite surse de zgomot, in relatie cu fluctuatiile de cantitate de neuro-transmitator chimic, eliberata la conexiunea sinaptica, implica o relatie de intrare-iesire de tip probabilistic.
Intervalul de timp dintre momentul emisiei unui semnal la soma neuronului pre-sinaptic si momentul emisiei unui semnal indus de catre neuronul post-sinaptic, este de aproximativ 1-2 msec. De aici rezulta ca un neuron poate avea o emisie maximala de circa 500-1000 semnale pe secunda, care intr-o retea neuronala este redusa de circa 3-5 ori.
Din aceste considerente de dinamica a activitatii neuronale, se poate observa faptul ca neuronul biologic este un dispozitiv biologic lent in comparatie cu dispozitivele electronice construite de om - acestea pot fi chiar de sute de mii de ori mai rapide decat un neuron biologic. Cu toate acestea, orice sistem de calcul bazat pe dispozitive electronice are performante inferioare creierului uman constituit din neuroni. Concluzia evidenta este ca puterea de calcul al creierului uman nu este datorata vitezei de procesare a neuronilor constitutivi, ci largii interconectari a unor dispozitive biologice lente - neuronii, care efectueaza operatii simple: integrarea semnalelor sosite de-a lungul arborelui dendritic si emisia unui semnal de-a lungul axonului, daca semnalul de intrare integrat depaseste nivelul de activare.
Modificarea tariei sinaptice este rezultatul unui proces de "invatare" [113]. Legatura sinaptica si modul de procesare a semnalelor de catre neuron formeaza mecanismul de baza al capacitatii de memorare al creierului.
2. Neuronul artificial.
Intr-o retea neuronala artificiala, unitatea analoga neuronului biologic este o unitate de procesare simpla, care va fi numit neuron artificial, sau mai simplu tot neuron.
Un neuron artificial are mai multe cai de intrare care corespund arborelui dendritic. Celei de-a i-a cale de intrare in neuronul al j-lea ii corespunde o valoare numerica reala xi, echivalentul semnalului electric din modelul biologic al neuronului. Fiecare marime de intrare xi este ponderata valoarea numerica reala wji, echivalentul tariei sinaptice din modelul biologic al neuronului. Valoarea xi wji reprezinta al i-lea semnal de intrare dendritic in al j-lea neuron artificial.
Aceste valori sunt integrate (sumate), proces similar celui realizat de soma neuronului biologic.
Suma
ponderata![]()
![]() reprezinta argumentul unei functii, numita functie de activare care va
determina valoarea de iesire axonica yi din neuron. Cele mai utilizate functii de activare
sunt:
reprezinta argumentul unei functii, numita functie de activare care va
determina valoarea de iesire axonica yi din neuron. Cele mai utilizate functii de activare
sunt:
-
functia liniara: ![]()
-
functia treapta (Heaviside): ![]()
-
functia rampa: 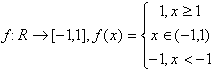
-
functia sigmoidala: ![]()
-
functia tangenta hiperbolica: ![]()
![]()
-
functia signum: ![]()
Acestea sunt exemple de functii de activare care sunt cel mai frecvent utilizate. Functia de activare depinde de modelul de retea neuronala ales si de tipul problemei pe care dorim sa o rezolvam, alegerea sa nefiind constransa de nici o conditie, decat eventual de analogia cu modelul biologic. Valoarea obtinuta prin aplicarea functiei de activare este propagata pe caile de iesire, echivalente arborelui axonic din modelul biologic. In Fig.2.2. avem reprezentarea schematica a neuronului artificial.
|
|
Fig. 2.2. Reprezentarea schematica a neuronului artificial. Indicele j reprezinta al j-lea neuron din reteaua neuronala artificiala.
In concluzie, neuronul artificial efectueaza urmatoarele operatii:
Integrare(Sumare): ![]()
Activare(Transfer): ![]()
![]() )
)
Acest model matematic al neuronului artificial, propus pentru prima data de McCullogh si Pitts [104], desi foarte simplu, reprezinta o unitate de calcul foarte puternica. McCullogh si Pitts au demonstrat ca un ansamblu de neuroni artificiali interconectati este capabil in principiu sa efectueze orice calcul, cu conditia alegerii corespunzatoare a tariilor sinaptice wji. Acest lucru inseamna ca un ansamblu de neuroni artificiali interconectati intr-un ansamblu numit retea neuronala, poate efectua orice calcul pe care poate sa-l efectueze un sistem de calcul clasic, chiar daca nu intotdeauna la fel de repede sau convenabil.
3. Diferente intre neuronul biologic si neuronul artificial.
Neuronul biologic comporta totusi multe alte elemente care in simplul model al neuronului artificial au fost cu buna stiinta omise [68]. Cele mai semnificative diferente sunt urmatoarele:
- Neuronul biologic raspunde la semnalele de intrare intr-un mod continuu si nu discret, ceea ce se numeste raspuns gradual. Dar relatia neliniara dintre semnalul de intrare si semnalul de iesire la un neuron biologic este o trasatura universala, care apare si la neuronul artificial prin intermediul functiei de activare.
- Neuronii biologici nu au toti acelasi moment fix de activare (t t + 1) si nici nu actioneaza sub controlul central al unui tact generat de un ceas.
- Cantitatea de substanta neuro-transmitatoare eliberata de sinapsa poate varia intr-un mod impredictibil. Acest efect poate fi modelat, considerand o generalizare stohastica a dinamicii modelului determinist McCullogh - Pitts.
Chiar daca uneori vom face apel la realismul biologic, vom fi interesati de trasaturile si capacitatea de calcul ale modelului de retea neuronala artificiala si nu de aplicabilitatea directa in modelarea creierului. Legatura dintre retelele neuronale biologice si artificiale nu este importanta la nivelul modelarii detaliate, ci la nivelul reprezentarii si la nivelul algoritmic [100]. Desi implementarile biologice si artificiale ale algoritmilor sunt diferite, totusi exista numeroase trasaturi comune la nivel algoritmic.
Obs.2.1.: Termenul xo se numeste bias, avand o valoare constanta xo = +1 sau xo = -1. Rolul termenului bias este de a permite includerea implicita sau explicita a nivelului de activare qi care reprezinta pragul de activare al neuronului artificial.
De
exemplu, presupunand ca avem functia de activare signum, ![]()
![]()
![]() , atunci putem avea:
, atunci putem avea:
Nivel de activare qi explicit
Integrare:![]()
![]() ,
Activare:
,
Activare: ![]() , sau
, sau
Nivel de activare qi implicit:( notand![]() ,
x0 = -1)
,
x0 = -1)
Integrare:
![]() , Activare:
, Activare: ![]()
In cele ce urmeaza vom considera nivelul de activare implicit sau explicit, in functie de necesitati, fara ca aceasta sa influenteze intr-un fel generalitatea rezultatelor obtinute.
4. Retele neuronale artificiale.
Retelele neuronale artificiale sunt constituite din numerosi neuroni artificiali interconectati intre ei. Neuronii constituenti sunt de obicei organizati in multimi distincte numite straturi (layers). Exista cazuri de retele neuronale particulare, avand o topologie speciala, cand neuronii nu sunt organizati pe straturi bine definite, ci pe anumite submultimi.
O retea neuronala clasica consta dintr-o secventa de straturi de neuroni, cu conexiuni totale sau aleatore intre neuronii continuti in straturi succesive. Intotdeauna vom avea pentru o retea neuronala, cel putin doua straturi de neuroni, ce au rolul de a comunica cu mediul exterior:
- un strat de intrare : care are rolul de a prelua datele de intrare xi, i = 0,¼,n cu termen bias ( vezi Obs. 1.1) x0 = 1, sau i = 1,¼,n fara termen bias. Vectorul x = (x0, x1,, xn) sau x = (x1, x2,, xn) va fi numit vector de intrare al retelei neuronale.
- un strat de iesire : unde se obtin rezultatele yj, j = 1,¼,m furnizate de reteaua neuronala, ca raspuns la vectorul de intrare prezentat la stratul de intrare si al propagarii acestor date de la stratul de intrare catre stratul de iesire. Vectorul y = (y1, y2,, ym) se numeste vector de iesire al retelei neuronale.
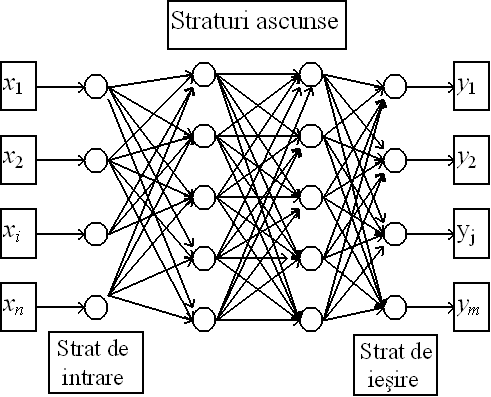
Fig. 2.3. Arhitectura generala a unei retele neuronale.
Toate celelalte straturi ale retelei neuronale, daca exista, diferite de stratul de intrare si de stratul de iesire vor fi denumite straturi ascunse (hidden layers).
Obs. 2.2. Cand vom spune despre o retea neuronala ca are n straturi, nu vom lua in calcul si stratul de intrare, ceea ce inseamna ca vom avea n - 1 straturi ascunse + stratul de iesire.
Neuronii din stratul de intrare au intotdeauna ca si functie de activare functia liniara, rolul lor fiind doar de-a propaga catre stratul succesor vectorul de intrare. Ceilalti neuroni, din celelalte straturi, pot avea orice functii de activare.
5. Modul de operare al retelelor neuronale.
Vom considera in cele ce urmeaza retele neuronale directe (feed-forward), la care propagarea informatiilor se face de la stratul de intrare catre stratul de iesire, fara a exista conexiuni intre neuroni dintr-un acelasi strat sau catre neuronii situati intr-un strat predecesor.
Retelele neuronale care contin legaturi sinaptice intre neuroni continuti in acelasi strat sau intre neuronii unui strat oarecare si neuronii unui strat predecesor se numesc retele neuronale recurente (feedback).
Vom presupune ca avem o retea neuronala cu l straturi (vezi Obs.2.2),
cu urmatoarea configuratie:
- n neuroni in stratul de intrare.
- nj neuroni in cel de-al j-lea strat ascuns, j = 1,, l - 1.
- m neuroni in stratul de iesire.
-
![]() taria sinaptica dintre neuronul al i -lea situat in stratul k - 1 si neuronul al j -lea situat in stratul k.
taria sinaptica dintre neuronul al i -lea situat in stratul k - 1 si neuronul al j -lea situat in stratul k.
- fk functiile de activare corespunzatoare stratului k, k = 1,2,,l.
Modul de operare al retelei neuronale directe este urmatorul:
- pentru stratul de intrare 0: prezentarea vectorului de intrare x = (x0, x1,, xn) ;
- pentru stratul 1:
Integrare: ![]() ;
;
Activare: ![]() ;
;
- pentru stratul ascuns k, k = 2,, l - 1;
Integrare: ![]() ;
;
Activare: ![]()
![]() ;
;
- pentru stratul de iesire l:
Integrare: ![]() ;
;![]()
Activare: ![]() ;
;
Pentru a putea implementa o problema folosind calculul neuronal, respectiv pentru a construi o retea neuronala relativ la acea problema, vom avea de parcurs doua etape principale:
a). Invatare(Antrenament).
b). Generalizare.
Invatarea (antrenamentul). Reprezinta procesul de modificare a tariilor sinaptice ca raspuns la vectorul de intrare prezentat la stratul de intrare al retelei neuronale (uneori si a vectorului tinta prezentat la stratul de iesire al retelei neuronale), in scopul configurarii retelei neuronale pentru a executa actiunea dorita.
Modificarea tariilor sinaptice in procesul de invatare se poate efectua in doua moduri:
-
Invatare
supervizata. Modificarea tariilor sinaptice este facuta pe baza
comparatiei dintre vectorul de iesire y
= (y1, y2,, ym) obtinut la stratul de iesire l
si vectorul tinta ![]() ,
ce reprezinta rezultatul dorit a se obtine la stratul de iesire, cand la
stratul de intrare s-a prezentat vectorul de intrare
,
ce reprezinta rezultatul dorit a se obtine la stratul de iesire, cand la
stratul de intrare s-a prezentat vectorul de intrare ![]() din multimea de antrenament. Vectorul tinta
din multimea de antrenament. Vectorul tinta ![]() este furnizat de un profesor (antrenor), de
unde si denumirea de invatare supervizata. Invatarea supervizata presupune
prezentarea de catre un antrenor a unor perechi de date de forma
este furnizat de un profesor (antrenor), de
unde si denumirea de invatare supervizata. Invatarea supervizata presupune
prezentarea de catre un antrenor a unor perechi de date de forma ![]() ,
ce formeaza o multime de date, numita multime de antrenament. Diferenta
dintre raspunsul obtinut y si
raspunsul dorit z este folosita
pentru a modifica tariile sinaptice, pe baza unui algoritm specific, numit lege
de invatare.
,
ce formeaza o multime de date, numita multime de antrenament. Diferenta
dintre raspunsul obtinut y si
raspunsul dorit z este folosita
pentru a modifica tariile sinaptice, pe baza unui algoritm specific, numit lege
de invatare.
Un caz particular al invatarii supervizate il reprezinta invatarea intarita (reinforcement), unde un profesor semnaleaza doar faptul daca raspunsul generat de reteaua neuronala este corect sau nu, fara ca sa stim care este marimea lor.
- Invatare nesupervizata. Sunt situatii cand nu putem defini scopul procesului de invatare sub forma unor rezultate dorite sau a unor rezultate corecte. Singura informatie disponibila consta din modul de corelare a datelor de intrare. Scopul acestui tip de invatare este ca reteaua neuronala sa creeze categorii din aceste corelatii, producand date de iesire corespunzatoare categoriei datei de intrare.
Generalizarea. Dupa ce reteaua neuronala a fost invatata pe baza unui numar suficient de exemple, ea va fi capabila sa induca o relatie completa de interpolare sau extrapolare a exemplelor invatate. Generalizarea reprezinta faza de raspuns a retelei neuronale, cand prezentandu-i-se vectori de intrare noi sau din multimea de antrenament, vectorul de iesire va fi cel asteptat, cu o posibila eroare foarte mica. Calitatea raspunsurilor in faza de generalizare reprezinta telul fazei de invatare - trebuie sa invatam reteaua neuronala pana cand va generaliza suficient de bine.
Modul de operare al retelei neuronale poate fi influentat de modul de operare al neuronilor dintr-un strat, pe baza a doua operatii posibile:
- Normalizarea. Reprezinta procesul de scalare a vectorului de iesire al unui strat al retelei neuronale, astfel incat suma totala a componentelor acestui vector sa fie constanta. Acest lucru este intalnit si la retelele neuronale biologice, unde neuronii de pe un strat sunt conectati la ceilalti neuroni ai aceluiasi strat, facand posibil ca fiecare neuron sa-si auto-ajusteze semnalul de iesire in concordanta cu semnalul total de iesire a stratului. Rezultatul operatiei de normalizare este ca pastreaza un nivel constant de activitate la nivelul unui strat de neuroni.
- Competitia (concurenta). Reprezinta procesul de interactiune al unui neuron de pe un strat al retelei neuronale, cu ceilalti neuroni de pe acelasi strat. Neuronul sau un grup de neuroni care genereaza valori de iesire maximale, vor fi declarati "castigatori", fiind singurii a caror valoare de iesire va fi propagata mai departe.
Retelele neuronale ce contin straturi cu mod de operare competitiv, le vom numi retele neuronale competitive, iar cele care nu contin straturi competitive le vom numi retele neuronale pasive.
6. Taxonomia retelelor neuronale.
Avand in vedere caracteristicile unei retele neuronale prezentate in paragraful precedent, si anume [63]:
- functii de activare liniare vs. functii de activare neliniare;
- mod de operare direct (feedforward) vs. mod de operare recurent;
- lege de invatare supervizata vs. lege de invatare nesupervizata;
- straturi concurente vs. straturi pasive;
Putem prezenta o privire de ansamblu asupra realizarilor de pana acuma in domeniul calculului neuronal, si anume o taxonomie a retelelor neuronale. Fara a avea pretentia de a cuprinde in totalitate diversa clasa de retele neuronale existenta, totusi cele patru caracteristici de mai sus permit o incadrare a majoritatii retelelor neuronale.
Clasificarea retelelor neuronale:
- liniare
- directe
- invatare nesupervizata
Asociator liniar:
- Anderson (1976) [7];
- Willshaw (1969) [167];
- invatare supervizata
Regresii liniare multiple:
- Kohonen (1988);
- recurente
- invatare supervizata
- competitiv
Art - Adaptive Resonance Theory:
- Grossberg (1987) [60];
- pasiv
Boltzmann, Recurrent Back-Propagation,
Jordan Nets:
- Ackley, Hinton & Sejnowski (1985);
- Pineda (1989);
- Jordan (1986);
- invatare nesupervizata
- competitiv
Art - Adaptive Resonance Theory:
- Grossberg (1987) [60];
- pasiv
BSB - Brain State in a Box, Hopfield Nets,
Interactive Activation:
- neliniare
- directe
- invatare nesupervizata
- competitiv
Feature Maps:
- Kohonen (1983) [87];
- pasiv
Infomax:
- Linsker (1987);
- invatare supervizata
- competitiv
Competitive Learning:
- Rumelhart & Zipser (1986) [134][135][136];
- pasiv
Perceptron, Delta-Rule, Back-Propagation:
- Rosenblatt (1962) [132];
- Widrow & Hoff (1960) [165];
- Rumelhart & al. (1986) [136];
- recurente
- la fel ca la retele neuronale liniare-recurente.
7. Calculul neuronal versus Inteligenta artificiala si calculul traditional.
Folosind termeni de informatica, am putea descrie creierul ca un sistem de calcul paralel compus din aproximativ 1011 procesoare. Folosind modelul simplu McCullogh-Pitts, rezulta ca fiecare procesor executa un program foarte simplu: integrare si activare (I.1.1.2). Faza de activare reprezinta generarea unui semnal de iesire, reprezentat printr-un numar real y, care semnal este propagat catre alte "procesoare" (neuroni), care la randul lor efectueaza un calcul similar.
Diferenta dintre acest mod de procesoare al informatiilor si procesarea clasica von Neumann este evidenta. In calculul neuronal avem un numar mare de procesoare, fiecare executand un calcul simplu (integrare-activare), spre deosebire de calculul traditional unde unul sau cateva procesoare executa secvente complexe de calcule.
Un algoritm reprezinta descrierea unei secvente de instructiuni si ordinea de executie a acestor instructiuni, care au ca scop atingerea unui tel. Evident aceasta definitie nu cuprinde nici pe departe trasaturile fundamentale ale calculului algoritmic. De aceea, cea mai buna cale de a caracteriza calculul neuronal este de a enumera caracteristicile echipamentelor pe care algoritmul se implementeaza, adica calculatorul von Neumann:
n o singura unitate centrala (CPU);
n Efectuarea calculelor in ordine secventiala;
n O multime mare de instructiuni prin care se descrie algoritmul;
n Instructiunile pentru descrierea algoritmului sunt stocate in memorie;
n Operanzii folositi in calcule, precum si rezultatele obtinute sunt stocate in memorie, la locatii bine stabilite;
n Datele necesare algoritmului sunt localizate.
Descrierea de mai sus corespunde tipului de calcul secvential, cunoscut sub numele de SISD (Single Instruction Single Datastream) . Variatiile invocate in cadrul calculului paralel nu reprezinta altceva decat variante ale SISD:
SIMD (Single Instruction Multiple Datastream): fiecare instructiune opereaza pe mai multe date [71].
MISD (Multiple Instruction Single Datastream): mai multe instructiuni opereaza in paralel asupra unor date, o instructiune pe data, dar mai multe instructiuni simultan. Denumirea consacrata este de arhitectura pipeline.
MIMD (Multiple Instruction Multiple Datastream): mai multe operatii opereaza pe mai multe date simultan. Acest lucru se reduce de obicei la mai multe masini SISD interconectate.
Chiar daca aceste variante sisteme de calcul pot implementa calcul algoritmic paralel, ceea ce duce la o eficientizare a vitezei de calcul, trasatura fundamentala ramane procesarea secventiala a datelor.
Din cele prezentate pana acuma sa incercam sa caracterizam calculul neuronal:
n exista un numar mare de elemente de procesare (neuroni);
n fiecare element de procesare efectueaza un numar mic de calcule simple (adunari, inmultiri, comparatii);
n fiecare element de procesare este conectat la multe alte elemente de procesare;
n numarul de conexiuni dintre elementele de procesare este mult mai mare decat al elementelor de procesare;
n taria legaturii dintre elementele de procesare este variabila, si ceea ce este foarte important, este faptul ca reteaua neuronala isi modifica singura taria acestei legaturi;
n daca la un sistem de calcul von Neumann, instructiunile care se executa de elementul de procesare caracterizeaza deplin actiunea de executat, la o retea neuronala elementele de procesare efectueaza calcule simple independente de actiunea de executat;
n reteaua neuronala invata cum sa execute actiunea dorita prin antrenament (experienta); de aceea ea nu este programata prin intermediul unui set de reguli descrise a priori;
n informatia este distribuita in reteaua neuronala fiind stocata in tariile legaturilor sinaptice dintre neuroni;
Comparatia dintre caracterizarea calculului algoritmic si calculului neuronal scoate in evidenta urmatoarea concluzie:
Calculul algoritmic necesita programare, adica stabilirea unui set de reguli care sa caracterizeze a priori calculul ce urmeaza a fi implementat pe calculator;
Retelele neuronale invata, ele "absorb" experienta, modificandu-si structura interna in scopul efectuarii actiunii dorite.
7.1. Programare versus invatare.
Spre deosebire de sistemele expert dezvoltate ca elemente de AI, unde baza de cunostinte este explicitata sub forma unui set de reguli implementate de un programator cu un anumit limbaj de programare, calculul neuronal, respectiv retelele neuronale isi genereaza propriile seturi de reguli din invatarea exemplelor invatate. Invatarea este realizata pe baza unei legi de invatare care ajusteaza tariile sinaptice ale retelei neuronale ca raspuns la exemplele de antrenament.
Pentru ca reteaua neuronala sa execute task-ul dorit, nu este nevoie sa scriem nici un fel de program. Trebuie doar sa invatam reteaua, prin prezentarea unui numar suficient de exemple relevante, cu scopul de a ajunge la o generalizare performanta.
Daca intr-un model de calcul traditional - program, sistem expert - apar cereri de informatii noi sau cereri de a modifica informatiile existente, setul de reguli care implementeaza baza de cunostinte nu este capabila sa interpoleze raspunsul dorit. Programatorul, expertul, va trebui sa construiasca noi reguli, folosind instructiunile unui limbaj de programare, testand interactiunea acestor noi reguli cu cele vechi implementate. Putem defini principalul neajuns al sistemelor traditionale de calcul: imposibilitatea de a genera reguli noi sau de a le modifica automat pe cele vechi, reguli ce reprezinta baza de cunostinte a task-ului ce se doreste a fi rezolvat.
7.2. Memorii asociative.
O caracteristica importanta a calcului neuronal este modul de stocare a datelor de catre reteaua neuronala. Unitatea de memorare o reprezinta taria sinaptica. Stare curenta de cunostinte a retelei neuronale va fi caracterizata de valorile numerice reale ce corespund in acel moment tariilor sinaptice. O data de intrare in reteaua neuronala nu va fi stocata intr-o pozitie unica, ci va fi distribuita in reteaua neuronala, impartind spatiul de memorare si cu alte date de intrare.
Retelele neuronale pot fi utilizate si ca memorii asociative. Acest lucru inseamna ca dupa ce am antrenat reteaua neuronala, daca ii prezentam o data distorsionata din multimea de antrenament, reteaua neuronala va genera un raspuns similar cu cel al datei ne distorsionate. Un caz particular il reprezinta retelele neuronale auto-asociative, unde vectorul de intrare coincide cu vectorul de iesire. Prezentandu-i-se un vector de intrare distorsionat, la stratul de iesire vom obtine vectorul restaurat.
7.3. Toleranta la deteriorari.
Sistemele de calcul traditionale sunt inutilizabile la aparitia celui mai minor defect la unitatea de memorie. Este suficienta deteriorarea unui singur bit de memorie pentru ca datele memorate sa se altereze.
La retelele neuronale, deteriorarea unor neuroni sau a unor tarii sinaptice, nu atrage dupa sine o deteriorare abrupta a performantelor. Cu cat avem un grad mai mare de degradare al retelei neuronale, cu atat se deterioreaza performantele retelei neuronale, fara ca aceasta sa-si inceteze functionarea.
Toleranta la deteriorari a retelei neuronale este datorata modului distribuit de stocare a datelor. Toleranta la deteriorari este o caracteristica fundamentala a retelelor neuronale biologice. In sistemul nervos, zilnic se degradeaza cateva mii de neuroni, fara ca aceasta sa afecteze, cel putin pana la o anumita varsta, functionalitatea si robustetea activitatii sale.
Acest fenomen poate fi privit ca o trasatura fundamentala a evolutiei inteligentei [68].
7.4. Recunoasterea formelor (Pattern Recognition).
Sistemele de calcul neuronal sunt deosebit de eficiente in actiuni legate de recunoasterea formelor. Retelele neuronale s-au dovedit a fi mult superioare sistemelor statistice traditionale sau sistemelor expert.
Un exemplu elocvent de recunoastere a formelor este insasi abilitatea de a translata simbolurile de pe aceasta pagina in cuvinte, propozitii, fraze pline de continut. Recunoasterea formelor este o actiune care necesita capabilitatea de a cuprinde simultan o mare cantitate de informatii si de a emite raspunsuri generale. Recunoasterea formelor necesita sisteme de calcul capabile sa "inteleaga" date partiale sau deformate.
Retelele neuronale poseda capacitatea de a invata si de a construi structuri unice relative la o problema data, fiind din acest motiv deosebit de eficiente in recunoasterea formelor. Capacitatea retelelor neuronale de a selecta combinatii de trasaturi pertinente pentru o anumita problema le face sa fie superioare sistemelor statistice. De asemenea, capacitatea retelelor neuronale de a deduce aceste trasaturi pertinente, prin insasi modul lor de actiune si nu prin interventia deliberata a unui programator, le face sa fie superioare si sistemelor expert.
7.5. Sinteza.
Problema
invatarii retelelor neuronale diferite aplicatii continue, este echivalenta din
multe puncte de vedere cu problema aproximarii si interpolarii unei functii
continue [44], [45], [46]. In aceasta analogie, a invata reteaua neuronala cu
ajutorul unei legi de invatare supervizate, inseamna a determina acea functie
parametrica ![]() pentru care:
pentru care:
![]()
w reprezinta multimea tariilor sinaptice ale retelei neuronale. S-a demonstrat faptul ca retelele neuronale sunt aproximatori universali, fiind capabile sa aproximeze arbitrar de bine orice aplicatie continua [28], [36], [38], [41]. Aceasta capacitate a retelelor neuronale artificiale de a sintetiza functii continue complexe, este analoga cu abilitatea retelelor neuronale biologice de a invata miscari coordonate complexe, ca de exemplu de a folosi unelte, de a face sport.
8. Domenii de utilizare ale retelelor neuronale.
Din cele prezentate pana acuma, rezulta faptul ca retelele neuronale sunt utile intr-o gama foarte diversificata de aplicat Daca studiem literatura de specialitate relativ la domeniul aplicativ al retelelor neuronale, vom gasi aplicarea lor in toate domeniile activitatii umane. Pornind de la arta, stiinte naturale, stiinte sociale, industrie, agricultura, mergand pana la sport, divertisment, aproape ca nu existe domeniu in care sa nu gasim aplicatii ale calculului neuronal. Acest lucru nu este de mirare, deoarece analizand trasaturile calculului neuronal (vezi I.2) deducem caracterul sau universal. Totusi cea mai adecvata utilizare a calculului neuronal o reprezinta domeniile apropiate perceptiei si gandirii umane.
8.1. Procesarea limbajului.
8.1.1.Conversii text-limbaj.
T. Sejnowski si C. Rosenberg [144] au aplicat sistemele de calcul neuronal in domeniul translatarii unui text scris in limbaj vorbit. Proiectul lor numit Nettalk, a avut la baza o retea neuronala directa cu doua straturi, invatata pe baza unei legi de invatare supervizata.
Dupa cum se vede in Fig.1.6, reteaua neuronala Nettalk cuprinde un strat de intrare cu 7 neuroni, valorile admisibile de intrare fiind caracterele alfabetului englez si semnele de punctuatie. Stratul ascuns este constituit din 80 de neuroni, iar stratul de iesire din 26 de neuroni, fiecare corespunzand unei unitati fonetice, numita fonema. Reteaua neuronala a fost antrenata cu ajutorul unui dictionar de 1024 cuvinte. Dupa 10 sedinte de antrenament s-a obtinut o pronuntie inteligibila, iar dupa circa 50 de sedinte de antrenament s-a obtinut o acuratete de 95% in pronuntie.
S-a constatat faptul ca reteaua neuronala a reusit sa extraga din datele invatate o serie de trasaturi esentiale procesului de vorbire. Astfel, neuronii din stratul ascuns raspund diferentiat, prin valori de activare mai mari sau mai mici, la vocale sau consoane. Analizandu-se structura interna si modul de stocare a datelor in retea, s-a regasit insasi structura fonologica a limbii engleze. Deteriorari premeditate ale retelei neuronale Nettalk, au dus la o degradare continua si lenta a performantelor sale, dar nu catastrofala, deteriorare imediat recuperata printr-o noua faza de re antrenare
|
|
Fig. 2.4.: Arhitectura generala a retelei neuronale Nettalk.
Un produs similar de conversie text scris-text pronuntat, avand la baza un sistem expert, produs de firma DEC si numit DecTalk, a necesitat un efort urias de programare al unei echipe de 35 specialisti, timp de 2 ani de zile, fara a obtine un produs superior retelei neuronale Nettalk.
Aceeasi arhitectura ca la reteaua Nettalk a fost aplicata de Qian si Sejnowski [127] la determinarea structurii secundare a proteinelor, in scopul de a transcrie secvente de DNA pentru coduri de proteine.
8.1.2.Procesarea limbajelor naturale.
D. Rumelhart si J. McClelland [136] au introdus retelele neuronale in domeniul procesarii limbajului natural. Prin procesare a unui limbaj natural vom intelege studiul modului de constructie a regululilor unui limbaj.
D. Rumelhart si J. McClelland au studiat acest proces cu ajutorul unei retele neuronale capabile sa invete timpul trecut (Past Tense) al limbii engleze. Invatand reteaua neuronala, ea a progresat din faza unui incepator care face greseli de tipul bring-bringed, pana la o faza de specialist in care era capabila de a determina timpul trecut pentru verbe neregulate. Abilitatea retelei neuronale de a generaliza pe baza unor date incomplete si de a se auto-organiza, au permis ca reteaua neuronala sa genereze raspunsuri corecte cand i s-a prezentat un verb nou sau necunoscut.
8.2. Comprimarea datelor.
G.W. Cottrell, D.Zipser si P. Munro [25] au utilizat retelele neuronale in scopul de a comprima eficient informatii corespunzatoare unor imagini grafice. Imaginile grafice ocupa, in functie de rezolutia de reprezentare si de numarul de culori folosit, un spatiu de memorare foarte mare, ajungand pana la ordinul a cativa mega-octeti.
Compresia imaginilor reprezinta o necesitate practica, deoarece spatiul de memorare este foarte costisitor, si in acelasi timp timpul de transfer al unei imagini este evident influentata de dimensiunea spatiului de memorare necesar pentru respectiva imagine.
Sistemul de calcul neuronal conceput de Cottrell, Munro si Zipser are la baza o retea neuronala cu trei straturi, capabila a comprima o imagine, si bineinteles capabila si de a o decomprima fara distorsiuni. Este interesant de subliniat legea de invatare nesupervizata folosita pentru a invata reteaua neuronala, care a permis ca ea sa se auto-configureze, fara interventia specialistilor. Cu aceasta retea neuronala s-a reusit comprimarea datelor la un factor de 8:1, cu o decomprimare ireprosabila a imaginii originale.
8.3. Recunoasterea caracterelor.
Un domeniu important de utilizare a retelelor neuronale il reprezinta domeniul interpretarii vizuale si al clasificarii simbolurilor.
Recunoasterea scrisului de mana. Cercetatori ai companiei Nestor Inc. din SUA, au dezvoltat un sistem de calcul neuronal care are ca si dispozitiv de intrare a datelor o tableta digitizoare pe care se poate scrie cu ajutorul unui Light-Pen. Reteaua neuronala a fost antrenata cu diferite scrisuri de mana, ea fiind capabila sa interpreteze un scris de mana oarecare cu o inalta acuitate.
Exista un mare numar de sisteme de recunoastere optica a caracterelor, numite OCR (Optical Character Recognition). Ceea ce diferentiaza retelele neuronale fata de sistemele OCR traditionale este flexibilitatea. Dupa invatare, reteaua neuronala este capabila sa recunoasca o mare diversitate de scrieri si sa faca presupuneri pertinente relativ la caracterele confuze.
Cercetatorii companiei Nestor au construit o retea neuronala pentru scrierea japoneza (Kanji). Prin folosirea retelelor neuronale in acest domeniu, s-a facut posibila eliminarea dificultatilor de a cuantifica elementele specifice ale unui limbaj.
Prelucrarea imaginilor. K. Fukushima [51][52] a elaborat un sistem de calcul neuronal pentru recunoasterea imaginilor, cu aplicabilitate practica in domeniul recunoasterii caracterelor. Reteaua neuronala construita, are la baza un sistem performant de recunoastere a formelor, numit Neocognitron.
Neocognitronul este de fapt o retea neuronala cu mai multe straturi ce simuleaza modul de prelucrare a imaginilor de catre cortexul uman. Straturile ascunse succesive de neuroni ale Neocognitronului au rolul de a extrage trasaturi definitorii ale imaginii fara a fi influentate de orientare sau distorsiuni. La nivelul stratului de intrare formele sunt unic determinate, o data cu propagarea informatiei catre stratul de iesire, activandu-se doar anumiti neuroni, care corespund unor trasaturi definitorii ale imagin
8.4. Probleme combinatoriale.
Retelele neuronale au fost folosite cu succes la rezolvarea problemelor NP-complete (Non Polynomial). Este cunoscut faptul ca problemele combinatoriale NP-complete necesita timpi de calcul care cresc exponential cu numarul de date de intrare.
Ca o piatra de incercare, celebra problema a comisului voiajor care trebuie sa strabata un numar dat de orase, folosind drumul cel mai scurt, reprezinta un test de masura a performantelor unor retele neuronale. Literatura de specialitate contine un numar impresionant de solutii ale acestei probleme, majoritatea bazate pe o arhitectura particulara de retea neuronala, numita retea neuronala Hopfield.
Cercetatorii J. Hopfield si D. Tank [73], au fost primii care au aplicat calculul neuronal in domeniul rezolvarii problemelor combinatoriale NP-complete. Ei au construit o retea neuronala pentru a rezolva problema comis voiajorului, atasandu-i o functie energetica dependenta de starea neuronilor constituenti. Minimul functiei energetice, corespunde unei stari stabile a neuronilor, drumul minim fiind astfel regasit.
H. Szu [150] a imbunatatit reteaua neuronala construita de Hopfield si Tank, utilizand o functie energetica care conduce la stari mai stabile si prin urmare la solutii mai performante.
8.5. Recunoasterea formelor.
8.5.1. Clasificarea formelor.
Dupa cum am aratat, in domeniul recunoasterii formelor (pattern recognition), sistemele de calcul neuronal au performante superioare sistemelor expert sau sistemelor clasice de calcul. Exista o gama foarte diversificata de aplicabilitate a sistemelor de calcul neuronal in acest domeniu. Unul din exemplele semnificative, il reprezinta aplicarea retelei neuronale de tipul BP (Back Propagation) in clasificarea tintelor radar. R. Gorman si T. Sejnowski [59] au construit o retea neuronala tip BP cu doua straturi; stratul de intrare contine un numar de 60 de neuroni, corespunzand la cele 60 benzi de frecventa necesare detectarii unei tinte radar, stratul de iesire al retelei neuronale, contine un numar de neuroni corespunzand la numarul de tinte radar; stratul ascuns are un numar de 12 neuroni.
Dupa faza de antrenament, reteaua neuronala s-a comportat ca un operator radar super calificat.
8.5.2. Control industrial.
Foarte bune rezultate s-au obtinut aplicand retelele neuronale tip BP la recunoasterea imaginilor furnizate de camere video, pentru a conduce un robot. D. Glover [58] a folosit pentru digitalizarea imaginilor video un procesor optic Fourier, care lucreaza in timp real. Reteaua neuronala era constituita din 2 straturi: stratul ascuns cu un numar de 20-40 neuroni, iar stratul de iesire un numar corespunzator de neuroni de comanda pentru robot. Aplicand aceasta retea neuronala in domeniul controlului industrial, s-au obtinut rezultate interesante.
In cadrul cercetatorii conduse de Glover, s-a pus in evidenta pentru prima data fenomenul de supra-antrenament (overtraining), adica faptul ca prezentarea unui numar prea mare de exemple de antrenament poate duce la distrugerea datelor memorate pana atunci. Acest lucru se explica prin faptul ca reteaua neuronala se auto-configureaza initial in concordanta cu tendinta statistica a datelor de antrenament, prezentarea unor noi date irelevante producand deviatii de la tendinta statistica generala.
Fenomenul de supra - antrenament este unul din principalele neajunsuri ale legilor de invatare supervizate care incearca sa invete date eronate sau ne relevante, implicand modificari semnificative asupra tariilor sinaptice, fata de ajustari minore ale tariilor sinaptice provocate de datele corecte, care genereaza erori minime.
8.6. Prelucrarea semnalelor.
8.6.1. Predictie.
Dupa cum se stie, problemele de predictie pentru serii haotice sunt dificil de rezolvat daca utilizam metode conventionale liniare sau polinomiale [64], [65]. Lapedes si Farbes [36] au construit o retea neuronala pentru predictia unei serii haotice, reprezentand solutiile numerice ale unei ecuatii diferentiale, cunoscuta sub numele de ecuatia Mackey-Glass [97]:
![]()
![]() (2.1)
(2.1)
unde a reprezinta un factor de intarziere.
Idea de baza consta in a antrena reteaua neuronala cu o multime de date de forma:
![]() (2.2)
(2.2)
iar ca date tinta, date cunoscute de forma ![]() .
Parametrul a controleaza haoticitatea
rezultatelor numerice.
.
Parametrul a controleaza haoticitatea
rezultatelor numerice.
Reteaua neuronala construita de Lapedes si Farbes are trei straturi, 2 straturi ascunse, un strat de iesire constituit dintr-un singur neuron liniar (cu functie de activare liniara). Ceea ce s-a constatat la aceasta retea neuronala este aparenta sa capabilitate de a reprezenta in straturile ascunse legea de generare a unei astfel de serii haotice.
8.6.2. Modelarea sistemelor, filtrarea semnalelor.
Aceeasi autori, Lapedes si Farbes, au obtinut rezultate interesante in domeniul modelarii unor sisteme. Incercarea lor, s-a bazat pe modelarea functiei corespunzatoare sistemului:
![]() (2.3)
(2.3)
Reteaua
neuronala continea in stratul de intrare doi neuroni, corespunzand valorilor ![]() si
si ![]() ,
iar stratul de iesire un singur neuron corespunzand valorii
,
iar stratul de iesire un singur neuron corespunzand valorii ![]() .
Reteaua neuronala avea doua straturi ascunse, fiecare strat avand cate 10
neuroni. Invatarea retelei s-a facut cu
ajutorul unor date corespunzand unor semnale cu banda unica limitata, ca o suma
de 20 de sinusoide. Desi, invatarea retelei neuronale s-a facut relativ la
ecuatia (1.3), ea a invatat de fapt forma generala a mecanismului de modelare,
comportandu-se satisfacator la semnale arbitrare prezentate la stratul de
intrare.
.
Reteaua neuronala avea doua straturi ascunse, fiecare strat avand cate 10
neuroni. Invatarea retelei s-a facut cu
ajutorul unor date corespunzand unor semnale cu banda unica limitata, ca o suma
de 20 de sinusoide. Desi, invatarea retelei neuronale s-a facut relativ la
ecuatia (1.3), ea a invatat de fapt forma generala a mecanismului de modelare,
comportandu-se satisfacator la semnale arbitrare prezentate la stratul de
intrare.
Retelele neuronale au fost folosite si in aplicatii de filtrare a semnalelor, cu scopul de a elimina zgomotul perturbator. S-au construit in acest fel retele neuronale aplicate in domeniul medicini [113], pentru a elimina zgomotul produs de imperfectiunea aparatelor de masura EKG, EEG, etc. Retelele neuronale sunt folosite si in domeniul telecomunicatiilor, pentru a elimina zgomotul si interferenta semnalelor.
8.7. Modelare economica si financiara.
Modelarea sistemelor economice si financiare cu scopul de a permite analize si prognoze eficiente, este de o foarte mare importanta. Determinarea unor elemente de tendinta economico-financiara cum ar fi consum, pret, inflatie, volum de vanzari, necesar de aprovizionat, etc., sunt in general greu de abordat datorita numarului mare de parametrii si a imprevizibilatii variatiei lor.
Retelele neuronale au capatat in acest domeniu o recunoastere semnificativa. Mari companii, cum ar fi Boeing, Volvo, Philips, folosesc sisteme de calcul neuronal in domeniul managementului firmei [113].
8.8. Servo-control.
Deosebit de dificila este problema controlului si conducerii unor sisteme complexe servo-mecanice (roboti). Dificultatea consta in a gasi metode computationale acceptabile pentru a compensa variatiile fizice din sistem. Desi uneori este posibil a construi formule matematice care sa descrie erori provocate de variatii fizice - erori provocate de alinierea axelor, deviatii ale organelor in miscare - doua probleme sunt de luat in considerare:
- Prima problema: de cele mai multe ori este aproape imposibil sa masuram cu acuratete variatiile fizice.
- A doua problema: complexitatea computationala necesara pentru a rezolva problemele variatiilor fizice poate fi ne fezabila din punct de vedere economic, necesitand o putere de calcul uriasa si echipamente speciale.
Cu toate acestea exista numeroase modele de calcul neuronal care stau la baza conducerii unor roboti. Un exemplu semnificativ este robotul comandat de o retea neuronala folosit pentru conducerea unui vehicul. D.Pomerleau [125] a construit in acest scop o retea neuronala cu doua straturi. Stratul de intrare consta dintr-o imagine digitizata de 30x32 pixeli si 8x32 pixeli de la un sistem video de proximitate. Stratul ascuns continea 29 de neuroni, iar stratul de iesire 45 de neuroni dispusi liniar. Neuronii din centrul stratului de iesire corespundeau pentru directia inainte, cei din stanga si dreapta pentru viraj stanga, respectiv dreapta.
Dupa ce reteaua neuronala a fost antrenata cu un numar de 1200 de imagini simulate, ea a fost capabila sa conduca un automobil cu o viteza de 25 km/h. Viteza limitata era datorata mai ales faptului ca echipamentul de calcul utilizat pentru a implementa reteaua neuronala, un microsistem Sun-3, nu avea viteza de calcul mare.
8.9. Teoria aproximar
Putem
considera o retea neuronala ca o implementare a unei reguli de calcul ce ne
permite sa obtinem un vector de iesire m-dimensional, cunoscand vectorul de
intrare n-dimensional corespunzator. Aceasta regula implementata de reteaua
neuronala corespunde de fapt unei clase de functii ![]() .
Exista suficiente rezultate care dovedesc ca retelele neuronale sunt din multe
puncte de vedere superioare metodelor de aproximare-interpolare polinomiale.
.
Exista suficiente rezultate care dovedesc ca retelele neuronale sunt din multe
puncte de vedere superioare metodelor de aproximare-interpolare polinomiale.
In aceste paragrafe am prezentat doar o parte a domeniului de aplicare a retelelor neuronale, fara a avea pretentia de a epuiza in totalitate posibilitatile de aplicare a calcului neuronal. Dupa cum am mai mentionat, retelele neuronale sunt modul de implementare a calculului neuronal, care este practic un instrument universal, cu avantaje si dezavantaje fata de metodele de calcul clasic sau cele bazate pe sistemele expert.
8.10. Clasificare.
Pentru a avea o imagine de ansamblu asupra modelelor de calcul neuronal construite pana in prezent, vom prezenta o clasificare a retelelor neuronale din punct de vedere al domeniului de utilizare.
|
Domeniul de utlizare |
Legea de invatare |
|
1.Predictie |
Supervizata |
|
2.Clasificare |
Supervizata |
|
3.Asociere de date |
Supervizata |
|
4.Conceptualizare de date |
Nesupervizata |
|
5.Filtrari de date |
Nesupervizata |
|
6.Optimizare |
Nesupervizata |
Vom prezenta in continuare retelele neuronale existente pentru fiecare domeniu de utilizare.
1. Retele neuronale pentru predictie:
|
Delta Bar Delta (DBD) |
Fiecare tarie sinaptica are propriul coeficient de invatare auto-ajustabil. |
|
Direct Random Search (DRS) |
Similar cu BP, incorporand un aspect aleatoriu, ce tine cont de invatarea cu succes a unor date. |
|
Extended Delta Bar Delta (EDBD) |
Fiecare tarie sinaptica are propriul coeficient de invatare si propriul coeficient inertial auto-ajustabil. |
|
Back-Propagation (BP) |
Modificarea tariilor sinaptice se face prin propagarea inapoi a erorii dintre vectorul de iesire si vectorul tinta, de la stratul de iesire catre stratul de intrare. |
|
Back-Propagation with Recirculation (BP_RCIRC) |
la fel ca la BP, dar este o retea neuronala auto-asociativa (I.2.2). |
|
Digital Neural Network Architecture (DNNA) |
Retea neuronala cu o lege de invatare speciala, care permite portarea retelei pe un chip siliconic produs de firma Neural Semiconductor din San-Diego. |
|
Self-Organizing Map into Back-Propagation (SOM_BP) |
Retea neuronala hibrida ce foloseste prima data o lege de invatare nesupervizata, pentru a separa conceptual datele de intrare, inainte de a fi folo-site pentru predictie. |
|
Cascade Corelation (Cascade) |
O varianta a modelului BP, unde neuronii din straturile ascunse sunt adaugati unul cate unul la arhitectura retelei, testandu-se la fiecare adau-gare performantele retelei neuronale. |
|
Adaptive Linear Network (Adaline) |
Reteaua neuronala cea mai simpla, constituita dintr-un singur neuron boolean. De interes istoric. |
|
Muliple Adaline Network (Madaline) |
Retea neuronala cu mai multe stra-turi, neuronii fiind elemente de procesare de tip Adaline. |
|
Simple Perceptron (PS) |
Retea neuronala directa cu un singur strat. |
|
Multy-Layer Perceptron (PMS) |
Retea neuronala directa cu doua sau mai multe straturi. |
2. Retele neuronale pentru clasificare.
La baza acestor retele neuronale sta metoda de auto-organizare dezvoltata de T. Kohonen [86].
|
Categorial Learning (Catlrnn) |
Fiecare categorie de iesire are propriul set de noduri pentru invatarea punctelor centrale ale datelor de intrare, avand un strat tip Kohonen fara functie de atractie. |
|
Counterpropagation (Cntrprop) |
Se invata relatia existenta intre stratul de iesire si stratul tip Kohonen. Stratul Kohonen nu are functie de atractie. |
|
Learning Vector Quantization (LVQ) |
Fiecare categorie de iesire are pro-priul set de noduri. Stratul Kohonen are un mecanism activ, bazat pe o functie de atractie si o metoda de limitare. |
|
Probabilistic Neural Networks (PNN) |
Sunt generate functii probabilistice empirice de probabilitate, utilizand re-tele neuronale pentru a implementa clasificatori Bayesieni. |
|
Self-Organizing Map into Categoriza-tion (SOM_CAT) |
Retea neuronala hibrida ce utilizeaza un strat Kohonen bidimensional, cu un mecanism activ de separare a datelor de intrare, inainte de a fi categorizate. |
3. Retele neuronale pentru asocieri de date.
|
Bidirectional Associative Memory (BAM) |
Reteaua neuronala invata perechi de vectori (A1,B1),(A2,B2),. Cand i se prezinta o versiune distorsionata a lui Ai, reteaua neuronala va genera perechea potrivita Bi. |
|
Boltzmann Pattern Completion (Boltzcmp) |
Reteaua neuronala invata o serie de vectori de date de intrare. Cand i se prezinta un vector de intrare distor-sionat, reteaua va genera vectorul restaurat. |
|
Boltzmann Input-Output (Boltzio) |
Retea neuronala avand un mod de operare similar cu retelele tip Hop-field, aparand in plus o lege de inva-tare speciala numita revenire simula-ta (simulated annealing). |
|
Hamming Network (Hamming) |
Un vector de intrare este comparat cu ceilalti vectori memorati, determinandu-se distanta minima la acestia pe baza unei distante specifice, numita distanta Hamming. |
|
Hamming Network with Lateral In-hibition (Hamlatin) |
Mod de operare similar cu cel al re-telei neuronale tip Hamming, dar selectarea unui vector se face printr-un proces similar cu cel biologic, nu-mit inhibitie laterala, de tip competitiv. |
|
Hopfield Network (Hopfield) |
Similar de modelul de retea neurona-la tip Hamming, insa foloseste o alta metoda de a determina distanta dintre doi vectori. |
|
Spatio-Temporal Pattern Recognition (SPR) |
O serie de vectori predefiniti sunt memorati initial, fiind folositi in continuare ca o baza de clasificare a vectorilor de intrare urmatori. Retea-ua permite acordarea sa pentru a detecta vectori variabili in timp. |
4. Retea neuronala pentru conceptualizare.
|
Adaptive Resonance Theory I (Art I) |
Retea neuronala care creeaza categorii ale datelor de intrare. Un factor de vigilenta urmareste si regularizeaza numarul de categorii formate. |
|
Self-Organizing Map (SOM) |
Datele de intrare sunt proiectate intr-o maniera similara cu cea intalnite la sistemele biologice, intr-un strat bidimensional. |
5. Filtrarea datelor.
|
Recirculation (recirc) |
Datele de intrare sunt netezite prin comprimare dupa care sunt restaurate. Reteaua neuronala se comporta ca un filtru pentru joasa frecventa, a carui punct de tranzitie este determinat de numarul din stratul ascuns. |
6. Optimizare.
|
Hopfield Network (Hopfield) |
Similar de modelul de retea neuronala tip Hamming, insa foloseste o alta metoda de a determina distanta dintre doi vectori. |
9. Tehnologii implicate in dezvoltarea calculului neuronal.
Din cele prezentate, rezulta ca aplicarea calculului neuronal este puternic influentata de dezvoltarea unor tehnologii corespunzatoare, care sa duca la o raspandire generala a calculului neuronal. Exista la ora actuala aproximativ 750 de firme [129], care au ca obiect de activitate dezvoltarea de sisteme de calcul neuronal, fara a mai pune la socoteala marile universitati , institute de cercetari, mari companii, unde exista departamente distincte de cercetare teoretica si aplicativa in domeniul calculului neuronal.
9.1. Simulatoare software.
Am subliniat in repetate randuri faptul ca trasaturile calculului neuronal il fac pe acesta sa fie diferit de calculul traditional (von Neumann), totusi cea mai accesibila metoda de a construi retele neuronale il reprezinta simulatoarele software, care ruleaza pe calculatoare clasice secventiale sau paralele. Aceasta idee nu este prea fericita, pentru ca in fond rapeste insasi idea fundamentala a calculului neuronal, calculul distribuit, trasatura care se pastreaza doar la nivelul de conceptie, nu insa si la cel de executie.
Lista simulatoarelor software existente pe piata comerciala este impresionanta. Din cele mai importante merita sa amintim Neural Works Professional II/Plus al firmei Neural Ware Inc. din Pittsburgh [113], BrainMaker al firmeii California Scientific Software, Neural Network Utility (NNU) al firmei IBM, Neural-Desk al firmei Neural Computer Sciences, MacBrain al firmei Neurix, NeuroWindows al firmei Ward Systems Group [129].
9.2. Acceleratoare hardware.
O imbunatatire adusa performantelor retelelor neuronale implementate prin intermediul simulatoarelor software pe calculatoare secventiale sau paralele, il reprezinta utilizarea acceleratoarelor hardware. Acceleratoarele hardware sunt circuite electronice specializate implementarii metodei calculului neuronal, degrevand unitatea centrala de un mare numar de operat Ele se ataseaza la calculatoarele clasice, transformandu-le in sisteme de calcul foarte rapide, care permit aplicatii de calcul neuronal in timp real. Vom prezenta cele mai importante realizari in acest domeniu, pentru o documentatie mai completa se poate consulta [34]:
- Mark III, Mark IV: produse de firma TRW din SUA, reprezinta procesoare de uz general pentru o mare gama de aplicatii in domeniul calcului neuronal. Contin un numar de circa 417.000 legaturi sinaptice, putand fi atasate ca un echipament periferic la un calculator din familia VAX.
- NEP (Network Emulation Processor): dezvoltat de firma IBM, reprezinta un accelerator hardware avand la baza un procesor VLSI. Cu ajutorul acceleratorului NEP se pot rula aplicatii complexe de calcul neuronal, fiind de obicei utilizat ca un emulator pentru PAN (Parallel Associative Network) al firmei IBM. NEP contine o serie de interfete locale de mare viteza, putand fi conectat in cascada la alte acceleratoare NEP, permitand retele neuronale de foarte mari dimensiuni.
- Anza, Anza Plus: acceleratoare hardware special construite pentru simularea modului de functionare a retelelor neuronale pe un mediu de calcul secvential. Anza este capabil de a realiza o putere de calcul de 150.000 de interconexiuni pe secunda. Aceasta unitate de masura, numar de interconexiuni pe secunda, este factorul de masura a performantelor computationale ale unei retele neuronale.
- Delta II: Procesor in virgula mobila, are o capacitate de calcul de 11.000.000 interconexiuni pe secunda, admitand o arhitectura de cuplare in cascada. Firma producatoare SAIC livreaza o data cu acceleratorul hardware si un mediu de dezvoltare de aplicatii avand la baza calculul neuronal.
9.3. Procesoare neuronale.
In ultima perioada s-au dezvoltat si implementat sisteme de calcul neuronal pe chipuri siliconice. Prezentam cateva realizari semnificative, o lista mai completa putand fi gasita in [34],[39],[145].
- ENN (Electronic Neural Network): Chip siliconic elaborat de firma AT&T, avand un numar de 256 neuroni si mai mult de 100.000 legaturi sinaptice. ENN este curent utilizat in domeniul compresiei imaginilor, cu scopul de a transmite imagini de mari dimensiuni in timp real pe linii telefonice.
- Silicon Retina, Silicon Ear: Chipuri care implementeaza elementele senzoriale ale vazului si auzului uman. Domeniul lor de aplicabilitate, mai ales in servo-control, biologie, medicina.
- 80170NX ETANN (Electrically Trainable Analog Neural Network): chip neuronal care permite un strat de intrare cu maximum 128 neuroni, putand efectua 64 de operatii de integrare la fiecare trei milisecunde. Firma producatoare Intel Neural Network Group.
9.4. Procesoare optice.
Procesoarele optice reprezinta o solutie care a dat foarte bune rezultate in domeniul calculului neuronal [145]. Aceste procesoare optice poseda multe trasaturi comune cu sistemele de calcul neuronal, fiind constituite din matrici de procesoare simple, analoge neuronilor din reteaua neuronala. De asemenea modul de operare al procesoarelor optice contine o larga scala de paralelism. Ca si realizari deosebite in utilizarea procesoarelor optice in calculul neuronal, mentionam:
- firma Hitachi din Japonia a construit un procesor optic corespunzand unei memorii auto-asociative cu doua straturi, avand topologia: 32-neuroni in stratul de intrare, 29 neuroni in stratul ascuns, 26 neuroni in stratul de iesire. Procesorul optic continea circa 1.000 neuroni/cm2.
- firma japoneza Mitsubishi a creat unul din cele mai puternice procesoare optice dinamice, avand o densitate de 2.000 de neuroni/cm2., cu un numar de 4 straturi de neuroni cu topologie variabila.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 3705
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved