| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
DETERMINAREA DDS INTR-UN REACTOR CONTINUU MULTIAMESTECAT
Modelele ideale de curgere (D si R), folosite pentru deducerea ecuatiilor reactoarelor D, respectiv R ideale, aproximeaza cu o eroare neglijabila un numar mare de reactoare. In numeroase alte cazuri insa, datorita existentei unor scurtcircuite (by-pass) prin care o parte de fluid ocoleste reactorul, formarii unor canale preferentiale, aparitiei unor zone stagnante in reactor, abaterile de la idealitate pot fi apreciabile si neglijarea lor poate duce la erori mari in proiectare.
Pentru a putea determina performanta unui reactor chimic, trebuie sa se cunoasca modul in care fluidul trece prin vas, mai exact trebuie sa se determine, in primul rand, distributia duratelor de stationare.
I. Scopul lucrarii
1) Determinarea duratelor de stationare (DDS) intr-un reactor experimental continuu prevazut cu multiagitare.
2) Propunerea unui model de curgere si calculul parametrilor acestuia.
II. Aspecte teoretice
Distributia duratelor de stationare a elementelor de fluid la iesirea din vas este caracterizata in mod uzual prin functia de repartitie a duratelor de stationare, F(t) si functia de densitate a distributiei, E(t).
Durata de stationare t reprezinta timpul scurs din momentul intrarii elementului de fluid in vas si pana la parasirea lui.
Functia de densitate a distributiei E(t) este astfel definita incat E(t) dt reprezinta fractia din elementele de fluid care au durata de stationare cuprinsa intre t si t+dt.
Functia E(t) este normata, astfel incat:
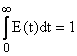 (1)
(1)
si are dimensiunea timp-1.
Functia E(t) se calculeaza din raspunsul sistemului la un semnal impuls utilizand relatia:
 (2)
(2)
Functia de repartitie a duratelor de stationare F(t) reprezinta fractia din elementele de fluid care au durata de stationare mai mica sau egala cu t.
Functia F(t) se calculeaza din raspunsul sistemului la un semnal treapta din relatia:
![]() (3)
(3)
unde c0 este concentratia trasorului la intrarea in reactor. Intre E(t) si F(t) exista relatia:
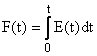 (4)
(4)
Functia E poate fi exprimata in functie de un timp
adimensional ![]() , unde
, unde ![]() reprezinta durata
medie de stationare (media distributiei):
reprezinta durata
medie de stationare (media distributiei):
 (5)
(5)
Dispersia distributiei, ![]() arata cat de imprastiate sunt duratele de
stationare in reactor ale elementelor de fluid fata de durata medie de
stationare:
arata cat de imprastiate sunt duratele de
stationare in reactor ale elementelor de fluid fata de durata medie de
stationare:
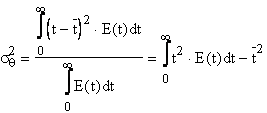 (6)
(6)
Caracteristicile distributiei in raport cu durata adimensionala vor fi:
- functia de densitate: ![]() (7)
(7)
- functia de repartitie: ![]() (8)
(8)
- media: ![]() (9)
(9)
Pentru modelarea acestui reactor tubular multiamestecat s-ar putea propune mai multe modele:
a) Modelul celular (serie RN)
|
Fig. 1. Modelul celular (serie RN) |
|
Fig. 2. Functia de densitate a distributiei pentru modelul celular |
Raspunsul modelului la semnal impuls este:
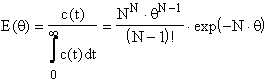 (10)
(10)
Dispersia este:
![]() (11)
(11)
Parametrul modelului este N, numarul de celule ideale, cu amestecare perfecta.
b) Modelul cu dispersie axiala
Raspunsul acestui model la semnal impuls este dependent de conditiile la limita asociate acestuia. Astfel, pentru conditiile la limita "vas deschis" (Gr. Bozga, O. Muntean, 2000; R. Mihail, O. Muntean, 1983) functia de densitate a DDS are expresia:
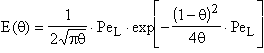 (12)
(12)
iar dispersia DDS este:
![]() (13)
(13)
|
Fig. 3. Modelul de circulatie cu dispersie axiala |
|
Fig. 4. Functia de densitate a distributiei pentru modelul cu dispersie axiala |
Parametrul modelului este ![]() ,
care se va calcula rezolvand ecuatia (13). Avand in vedere ipotezele fizice
avansate la constructia modelului, se poate aproxima
,
care se va calcula rezolvand ecuatia (13). Avand in vedere ipotezele fizice
avansate la constructia modelului, se poate aproxima ![]() = 2/PeL (modelul cu dispersie
axiala se potriveste doar la valori mari pentru PeL).
= 2/PeL (modelul cu dispersie
axiala se potriveste doar la valori mari pentru PeL).
Pentru alte conditii limita (de vas "inchis" etc.)
expresii similare pentru E(q) si ![]() sunt prezentate in Gr. Bozga, O. Muntean, 2000
si R. Mihail, O. Muntean, 1983.
sunt prezentate in Gr. Bozga, O. Muntean, 2000
si R. Mihail, O. Muntean, 1983.
III. Descrierea instalatiei experimentale
|
Fig. 5. Instalatia experimentala pentru studiul DDS intr-un reactor prevazut cu multiamestecare |
Instalatia experimentala, reprezentata in figura 5 (v. Fig. 6 - Schema instalatiei experimentale) se compune din: vasul de nivel constant V1, V2, fluometrul F2 si reactorul experimental RE3. Circulatia fluidelor in instalatie este dirijata si reglata cu robinetele R1, R2 si R6. Amestecatorul reactorului este actionat de motorul M3, a carui turatie este reglata cu reostatul A3.
Drept trasor se utilizeaza o solutie saturata de NaCl (electrolit), care modifica conductivitatea electrica a mediului. Pentru obtinerea raspunsului, concentratia trasorului la iesirea din reactor, s-a montat o sonda conductometrica SC3, conectata la conductometrul electronic CM prin intermediul unui comutator.
Reactorul RE3 este un vas tip coloana, cu multiagitare, alcatuit din 7 compartimente legate in serie, in fiecare aflandu-se cate un amestecator tip elice, actionat cu un ax comun. Volumul reactorului RE3 este de 800 cm3.
Debitele fluidului se determina prin masurarea volumului de fluid trecut prin reactor intr-un anumit interval de timp (se poate masura cu un cilindru gradat volumul iesit din reactor intr-un minut).
|
Fig. 6. Schema instalatiei experimentale V1, V2 - vase de nivel constant, alimentate de la retea; R1 R3, R6, R7 - robinete; F2 - fluometru; M3 - motor electric; RE3 - reactor experimental; S3 - seringa; sc3 - sonda conductometrica; A3 - reostat pentru reglarea turatiei agitatorului; CM - conductometru |
IV. Modul de lucru
In lucrarea de fata se va determina DDS cu ajutorul unui semnal impuls prin realizarea urmatoarelor etape:
- pregatirea instalatiei si a instrumentelor pentru experiment;
- realizarea semnalului impuls;
- culegerea datelor.
a) Pregatirea instalatiei si a instrumentelor
Se monteaza seringa continand trasorul.
Pentru umplerea reactorului RE3 se deschid robinetele R1, R2 si R6 (in succesiunea indicata). Umplerea se face cu un debit mai mare. Se fixeaza nivelul lichidului in reactor. Dupa ce reactorul s-a umplut se regleaza debitul de lucru dorit cu ajutorul robinetului R4. Se recomanda valori ale debitului cuprinse intre 80 si 120 cm3/min.
Se porneste motorul amestecatorului si se regleaza turatia dorita cu ajutorul reostatului.
Se masoara debitul de fluid ce trece prin reactor prin masurarea volumului de fluid strans intr-un cilindru gradat intr-un interval de timp dat, de ex. un minut. Pe toata durata experientei debitul de fluid trecut prin reactor trebuie sa ramana acelasi.
Se va
calcula durata medie de stationare ![]() .
.
Se conecteaza sonda la conductometrul electronic prin intermediul comutatorului corespunzator. Se alimenteaza conductometrul si se selecteaza scala de lucru (in mod obisnuit 0-5 mS).
b) Realizarea semnalului impuls
Se noteaza valoarea initiala a conductivitatii l (conductivitatea apei de la robinet), care trebuie sa fie aproximativ constanta.
Daca acul conductometrului arata constant aceeasi valoare se injecteaza trasorul (cca 5 ml solutie suprasaturata de NaCl) cu ajutorul seringii S3. Injectarea trasorului se va face prin apasarea rapida a pistonului seringii, dupa care seringa se va lasa in lacas. Momentul injectiei se considera t=0.
c) Culegerea datelor experimentale
Daca raspunsul nu se inregistreaza automat, indicatiile conductometrului se vor citi din 10 in 10 secunde pentru primele 60 de secunde si din 30 in 30 secunde pana la terminarea experientei. Datele se vor trece intr-un tabel de forma:
|
t |
3 |
|||||||||
|
l(t) |
Experienta se considera incheiata dupa un timp cel putin egal cu 3![]() (durata medie de stationare,
(durata medie de stationare, ![]() , a fost calculata la punctul 5).
, a fost calculata la punctul 5).
V. Prelucrarea datelor experimentale
a) Determinarea distributiei duratelor de stationare
Stabilirea evolutiei in timp a concentratiei trasorului la iesirea din reactor se face deci conductometric. Conductivitatea electrica a apei de robinet insa nu este zero. Va trebui atunci sa scadem din valoarea citita a conductivitatii initiale a apei, l . Practic pasii de calcul care trebuie efectuati sunt:
1. Reprezentarea variatiei concentratiei trasorului la iesire: c(t) l(t)-l
2. Calculul functiei de densitate E(t)
 (13)
(13)
Calculul integralei se poate numeric, prin metoda trapezelor, metoda Simpson, planimetrare, etc.
formula dreptunghiurilor:
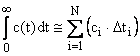 (14)
(14)
formula trapezelor (cand toate intervalele Dti sunt egale):
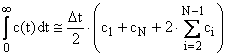 (15)
(15)
3.
Calculul duratei medii de stationare ![]() din datele experimentale (prin
metodele prezentate anterior).
din datele experimentale (prin
metodele prezentate anterior).
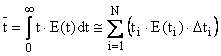 (16)
(16)
Se va compara ![]() astfel calculat cu
astfel calculat cu ![]() .
.
4. Calculul duratei adimensionale q
![]() (17)
(17)
5. Calculul functiei de distributie E(q
(q)=![]() E(t) (18)
E(t) (18)
6. Reprezentarea grafica E(q q
Aria=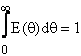 unde
unde 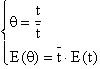
7.
Calculul dispersiei ![]() :
:
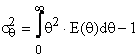 (19)
(19)
Datele experimentale obtinute se prezinta sub forma tabelului:
|
t, [s] |
c(t) l(t)-l |
E(t),[s -1] |
t E(t) |
|
E(q |
q E(q |
b) Determinarea parametrilor modelului de curgere
In functie de forma curbei E(q) se va propune un anumit model de curgere, caruia i se vor calcula parametrii. Modelele de curgere ce se pot utiliza in acest caz sunt :
1. Modelul celular (serie RN)
Parametrul acestui model, numarul de zone
amestecate perfect (N) se poate calcula cunoscand legatura dintre acesta si ![]() :
:
![]() (20)
(20)
trebuie remarcat ca numarul N poate lua si valori fractionare deoarece este o marime teoretica.
2. Modelul cu dispersie axiala
Parametrul care trebuie determinat este criteriul
PeL. Acesta se va calcula rezolvand ecuatia (13) (de exemplu prin
incercari succesive, pornind de la valoarea maxima ![]() =2/PeL).
=2/PeL).
VI. Continutul referatului lucrarii
Desenul instalatiei;
Descrierea in linii mari a experimentului si a instalatiei;
Tabelul continand valorile primare citite si valorile calculate;
Graficele conductivitate - timp, E(q q
Calculul parametrilor modelelor utilizate;
Concluzii privind concordanta datelor experimentale cu modelul de circulatie propus.
VII. Bibliografie
Gr. Bozga, O. Muntean, Reactoare chimice. Vol. 1 si 2, Ed. Tehnica, Bucuresti, 2000.
Gr. Bozga, s.a., Reactoare chimice. Caiet de aplicatii, Litografia IPB, 1991
R. Mihail, O. Muntean, Reactoare chimice, Ed. Didactica si Pedagogica, Bucuresti 1983.
O. Muntean, A. Woinarosky, G. Bozga, Aplicatii la calculul reactoarelor chimice, Ed. Tehnica, Bucuresti 1984.
O. Levenspiel, Tehnica reactiilor in ingineria chimica, Ed. Tehnica, Bucuresti 1967 (traducere din limba engleza).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1760
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved