| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Teoria cinetica a gazelor a fost initiata de D. Bernoulli si dezvoltata mai tarziu de R. Clausius, J. C. Maxwell si L. Boltzmann.
Teoria cinetica a gazelor presupune ca gazele sunt formate dintr-un numar foarte mare de molecule care se afla in miscare permanenta. Aceste molecule se considera sfere rigide si perfect elastice care poseda doar energie cinetica. Se neglijeaza orice interactiune intre molecule, cu exceptia ciocnirilor perfect elastice intre ele.
Miscarea moleculelor este total dezordonata si se numeste agitatie termica. Acestei miscari i se asociaza energia cinetica a moleculelor sistemului.
O modificare a energiei cinetice a moleculelor sistemului este inregistrata macroscopic ca o variatie a presiunii sau temperaturii sistemului. Miscarea particulelor implica ciocniri elastice frecvente intre ele si cu peretii vasului.
Legile mecanicii clasice se aplica miscarii particulelor.
Relatia fundamentala a teoriei cinetice a gazelor este:
![]() (2.39)
(2.39)
unde: p = presiunea gazului;
V = volumul gazului (cm3);
M = masa moleculara a gazului;
![]() = viteza medie patratica a moleculelor;
= viteza medie patratica a moleculelor;
n = numarul de moli de gaz.
Notand cu N numarul moleculelor din 1 cm3 gaz, rezulta:
![]() (2.40)
(2.40)
Relatia (2.39) devine:
![]() (2.41)
(2.41)
Energia cinetica totala a moleculelor dintr-un mol de gaz perfect este:
![]() (2.42)
(2.42)
Tinand cont de ecuatia de stare pentru gazul perfect si de relatia (2.39) avem:
![]() (2.43)
(2.43)
Pentru energia cinetica totala a moleculelor dintr-un mol de gaz perfect se obtine:
![]() (2.44)
(2.44)
Energia cinetica totala a moleculelor din n moli de gaz perfect este:
![]() (2.45)
(2.45)
Relatia (2.45) se poate scrie:
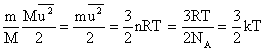 (2.46)
(2.46)
obtinandu-se energia cinetica medie a unei singure molecule.
unde: NA = numarul lui Avogadro = 6,02∙1023 molecule/mol;
k = constanta lui Boltzmann
Din relatia (2.46) se observa ca energia cinetica medie a moleculelor de gaz perfect este direct proportionala cu temperatura absoluta.
La temperatura de zero absolut energia cinetica devine nula, adica aici inceteaza agitatia moleculara. De aici reiese caracterul absolut al scarii de temperatura propusa de Kelvin.
Din relatia (2.43) rezulta
viteza medie a moleculelor unui gaz (![]() ):
):
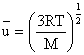 (2.47)
(2.47)
Relatia (2.47) arata ca cu cat temperatura este mai mare cu atat moleculele se deplaseaza mai rapid, iar la o temperatura data, moleculele grele se deplaseaza mai lent.
Introducand in relatia
(2.41) valoarea lui ![]() din (2.46) se obtine:
din (2.46) se obtine:
p = NkT (2.48)
Presiunea gazului perfect este direct proportionala cu numarul moleculelor din unitatea de volum si cu temperatura absoluta.
Din teoria cinetica a gazelor rezulta legea lui Dalton.
Pentru un amestec de gaze, presiunea acestuia este conform relatiei (2.41):
![]() (2.49)
(2.49)
Tinand cont de relatia (2.48) se obtine:
p = kT(N1 + N2 + ) (2.50)
Relatia (2.50) exprima legea lui Dalton, dupa care presiunea totala a unui amestec de gaze perfecte este suma presiunilor partiale.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1962
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved