| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Calculul erorilor autoinduse prin metoda erorilor primare BP≠BC. caz 1.
Calculul erorilor autoinduse prin metoda erorilor primare este o metoda exacta de determinare a erorilor autoinduse, care tine cont de toate componentele erorilor geometrice care pot sa apara. Astfel, se tine cont de urmatoarele erori:
erori dimensionale
erori de pozitie reciproca
erori de forma geometrica
erori de netezime
Deoarece obiectele de lucru instalate in dispozitiv nu au aceeasi dimensiune, abaterile dimensionale extreme ale acestora vor determina un ecart, respectiv un camp de dispersie in care vor fi incluse toate dimensiunile obiectelor de lucru, care vor fi instalate in dispozitiv. Pentru fiecare din erorile amintite anterior exista un asemenea camp de dispersie, care va fi caracterizat de o cota de gabarit, numita componenta aleatorie a erorii. Astfel, se definesc componentele aleatorii pentru urmatoarele erori:
eD - componenta aleatoare pentru erorile dimensionale;
eP - componenta aleatoare pentru erorile de pozitie;
eF - componenta aleatoare pentru erorile de forma;
eN - componenta aleatoare pentru erorile de netezime.
In cazurile in care acest camp de dispersie a componentelor aleatorii nu este dispus simetric fata de pozitia prescrisa a elementului geometric in studiu, atunci vor apare si componentele sistematice ale erorilor, care vor fi:
sD - componenta sistematica a erorilor dimensionale;
sP - componenta sistematica a erorilor de pozitie;
sF - componenta sistematica a erorilor de forma;
sN - componenta sistematica a erorilor de netezime.
Metoda erorilor primare consta in stabilirea variatiilor posibile ale bazei de cotare BC, a tipului de eroare primara care poate sa apara si in final, a sumei corespunzatoare a acestor erori primare componente, in vederea stabilirii erorii autoinduse totale.
Elementelor geometrice li se atribuie cate o dimensiune topologica DT, astfel:
DT = 0 pentru un punct (varf),
DT = 1 pentru o dreapta (muchie),
DT = 2 pentru un plan (suprafata, fateta).
Un element geometric al obiectului de lucru, avand o anumita dimensiune topologica DT, are atatea posibilitati de variatie, cate grade de libertate nu i-au fost preluate. De exemplu, un varf al unui obiect de lucru, daca este adus in contact cu un element de pozitionare, respectiv daca are un punct de contact cu dispozitivul, nu mai are nici o posibilitate de variatie.
Mentinerea permanenta in contact a varfului obiectului de lucru cu un punct al dispozitivului, elimina orice posibilitate de variatie a acestuia, respectiv elimina inducerea de abateri sau erori autoinduse.
O muchie cu dimensiunea topologica 1, daca este mentinuta in contact cu un singur punct care apartine dispozitivului, va avea eliminata posibilitatea de translatie a acestei muchii in raport cu dispozitivul, dar numai dupa normala pe muchie. Pot fi facute eventuale rotiri ale muchiei in raport cu acest punct. Sunt de asemenea posibile translatii ale muchiei dar numai dupa directia tangentiala la muchie.
O suprafata a obiectului de lucru daca este mentinuta in contact cu un punct (reazem) al dispozitivului, asa se elimina doar un grad de libertate a acesteia si anume, translatia dupa o directie normala la suprafata, dusa in punctul de contact cu diapozitivul. Translatiile dupa o directie tangenta la suprafata si rotirile in jurul punctului de contact sunt posibile.
Numarul gradelor de libertate preluate obiectului de lucru de catre dispozitiv este egal cu numarul teoretic al punctelor de contact, dintre cele doua, mai putin numarul gradelor de mobilitate ale mecanismului de pozitionare al dispozitivului, care au ca efect modificarea pozitiei obiectului de lucru.
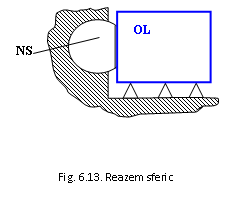 In fig. 6.13
se observa ca nuca sferica NS vine in contact cu obiectul de
lucru OL cu suprafata sa plana, deci are in contact 3 puncte
teoretice, dar avand o mobilitate in spatiu, deci 2m
(mobilitati), numarul gradelor de libertate (gl) care au fost
preluate de acest reazem sferic va fi: 3p - 2m = 1gl.
In fig. 6.13
se observa ca nuca sferica NS vine in contact cu obiectul de
lucru OL cu suprafata sa plana, deci are in contact 3 puncte
teoretice, dar avand o mobilitate in spatiu, deci 2m
(mobilitati), numarul gradelor de libertate (gl) care au fost
preluate de acest reazem sferic va fi: 3p - 2m = 1gl.
Un corp are 6 grade de libertate, respectiv 3 T (translatii) in lungul celor trei axe ale sistemului de referinta, X, Y, Z, si 3 R (rotatii) in jurul acelorasi axe notate A, B, C. Prin intermediul elementelor de pozitionare ale mecanismului de pozitionare, dispozitivul preia aceste grade de libertate ale obiectului de lucru (OL). Chiar in aceasta situatie punctele de contact ale mecanismului de pozitionare OL nu preiau complet gradele de libertate ale elementelor geometrice care compun OL. Cum dimensiunile OL care trebuie sa fie realizate sunt definite intre elemente geometrice ale OL, daca acestea nu sunt mentinute perfect invariante, se vor induce erori. Daca aceste erori sunt datorate abaterilor geometrice ale OL atunci acestea vor fi erori autoinduse.
Metodologia determinarii erorilor autoinduse depinde de gradul de coincidenta a bazei de pozitionare (BP) cu baza de cotare (BC). Pot fi trei cazuri de pozitii relative ale bazelor amintite:
I. Ne-coincidenta
bazelor ![]() ,
,
II. Coincidenta partiala ![]() , caz in care cele
doua baze coincid ca pozitie dar nu coincid ca dimensiune
topologica
, caz in care cele
doua baze coincid ca pozitie dar nu coincid ca dimensiune
topologica ![]()
III. Coincidenta totala ![]() , caz in
care cele doua baze coincid ca pozitie cat si ca dimensiune
topologica
, caz in
care cele doua baze coincid ca pozitie cat si ca dimensiune
topologica ![]() .
.
IV. Baza de cotare BC este interconvertibila cu baza de
fabricare BFa ![]() , in acest caz baza de
cotare (BC) si baza de fabricare (BFa) sunt generate simultan
de catre procesul de fabricare pe obiectul de lucru. Deci, nu se poate
face o distinctie clara care este baza de cotare si care este
baza de fabricare. Dimensiunea (cota) de realizat se stie ca este
cuprinsa intre baza de cotare (BC) si baza de fabricare (BFa).
, in acest caz baza de
cotare (BC) si baza de fabricare (BFa) sunt generate simultan
de catre procesul de fabricare pe obiectul de lucru. Deci, nu se poate
face o distinctie clara care este baza de cotare si care este
baza de fabricare. Dimensiunea (cota) de realizat se stie ca este
cuprinsa intre baza de cotare (BC) si baza de fabricare (BFa).
Pentru a se exemplifica metoda erorilor primare in determinarea erorilor autoinduse, se va considera cazul unui obiect de lucru pozitionat complet, supus unei operatii de gaurire.
I.
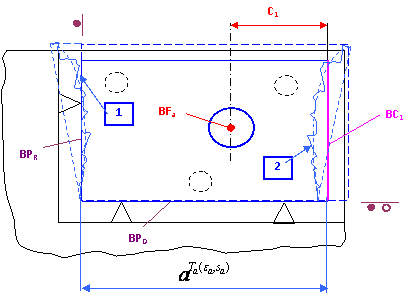 Cazul
Cazul ![]()
Fig. 6.14. Necoincidenta bazelor
Se poate constata ca baza de cotare BC1 are o alta pozitie decat baza de pozitionare corespunzatoare cotei C1. Suprafetele 1 si 2 ale obiectului de lucru pot avea abateri de localizare, pozitie, forma si netezime, asa cum este redat in fig. 6.14. Suprafetele 1 si 2 sunt definite de dimensiunea a corespunzatoare obiectului de lucru. Deoarece cele doua suprafete nu pot fi realizate perfect, a fost admis un camp de toleranta Ta pentru cota a. Abaterile de la localizare, pozitie, forma si netezime ale suprafetelor 1 si respectiv 2, avand in vedere ca se vor instala in dispozitiv mai multe obiecte de lucru, vor genera erori de dimensiune, pozitie, forma si netezime, care vor avea componentele aleatorii eD, eP, eF, eN, respectiv sistematice sD, sP, sF si sN. Aceste erori vor determina eroarea autoindusa la cota C1 a obiectului de lucru. Eroarea autoindusa va avea si ea o componenta aleatoare respectiv una sistematica.
Componenta aleatoare a erorii autoinduse pentru cota C1 este:
![]() .
.
Componenta sistematica a erorii autoinduse pentru cota C1 este:
![]() .
.
Indicii 1,2 arata ca erorile se refera atat la suprafata 1 cat si la suprafata 2 a obiectului de lucru.
Asa cum se observa in relatiile anterioare, toate erorile de dimensiune, pozitie, forma si de netezime, sunt cuprinse in componenta aleatore ea , respectiv in cea sistematica sa a cotei "a", care defineste pozitia relativa a bazei de cotare BC1 si, respectiv a bazei de pozitionare BPL.
Erorile autoinduse in acest caz sunt mari, fapt pentru care se recomanda ca acest caz de pozitionare sa se evite pe cat posibil.
Cazul BP=BC, BP≈BC. Cap.6.6..caz 2 si 3.
II.
Cazul coincidentei partiale ![]()
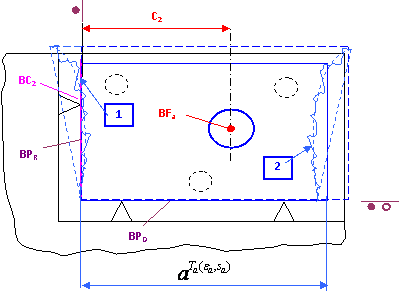
Fig. 6.15. Coincidenta partiala a bazelor.
In acest caz baza de cotare BC2, care estre un plan, deci are dimensiunea topologica DT=2, coincide ca pozitie cu baza de pozitionare de rezemare BPR. Baza BPR asigura un punct teoretic de contact cu obiectul de lucru, deci are dimensiunea topologica DT=0. Prin faptul ca desi BPR si BC2 coincid ca pozitie dar au dimensiuni topologice diferite, coincidenta lor este denumita coincidenta partiala.
Componenta aleatoare a erorii autoinduse la cota C2 este:
![]()
Componenta sistematica a erorii autoinduse la cota C2 este:
![]()
Se poate observa ca in acest caz erorile dimensionale ale obiectului de lucru, respectiv a cotei "a" nu mai influenteaza asupra erorii autoinduse pentru cota C2, iar pentru a scoate in evidenta acest lucru in relatiile (6.57) si (6.58) in locul erorilor dimensionale a fost scrisa cifra 0 (zero). De asemenea, eroarea autoindusa in acest caz depinde doar de erorile de pozitie, forma si de netezime ale suprafetei 1 a obiectului de lucru. Din acest motiv erorile autoinduse in cazul II, al coincidentei partiale, sunt mai mici decat cele din cazul I.
III.
Cazul coincidentei
complete ![]()
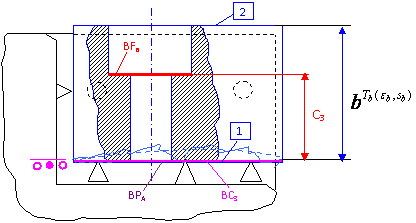
Fig. 6.16. Coincidenta totala a bazelor.
In acest caz baza de cotare BC3 este un plan (DT=2) si coincide ca natura cu baza de pozitionare de asezare BPA, care este de asemenea un plan (DT=2). Deoarece exista coincidenta de pozitie si coincidenta a dimensiunilor topologice, se poate spune ca exista coincidenta totala a celor doua baze.
Componenta aleatore a erorii autoinduse la cota C3 este:
![]()
Componenta sistematica a erorii autoinduse la cota C3 este definita de relatia:
![]()
Deoarece bazele care au coincidenta totala sunt suprafete plane (DT=2), eroarea autoindusa in acest caz nu depinde de erorile de dimensiune, respectiv de forma, motiv pentru care in relatiile anterioare in locul acestor erorii apare cifra 0 (zero).
Daca bazele cu coincidenta totala ar fi fost ambele drepte (curbe), atunci si erorile de forma s-ar anula in relatiile anterioare. In cazul cand coincid baze punctiforme, atunci atat componenta aleatoare cat si cea sistematica a erorii autoinduse sunt nule.
Se poate observa ca dintre cele trei cazuri de coincidenta I, II si III, ultimul este cel mai avantajos. El induce erori autoinduse minime. Acest caz este de preferat a se alege in faza de conceptie a dispozitivelor.
Un caz aparte il constituie cazul IV, cand in timpul procesului de fabricatie baza de cotare BC este realizata simultan cu baza de fabricare BFa,
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1560
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved