| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
REDUCEREA UNUI SISTEM DE FORTE APLICATE RIGIDULUI. TORSORUL DE REDUCERE. VARIATIA TORSORULUI CU PUNCTUL DE REDUCERE. INVARIANTI
Se considera un rigid actionat in punctele A1, A2,, An,
de fortele ![]() ,
, ![]() ,..,
,.., ![]() , (fig.2.12.a). Un punct oarecare Ai, raportat la polul O este definit de vectorul de pozitie
, (fig.2.12.a). Un punct oarecare Ai, raportat la polul O este definit de vectorul de pozitie ![]() . A calcula efectul mecanic produs in O de actiunea simultana a fortelor din sistemul dat
inseamna a reduce pe rand toate fortele sistemului, obtinand in O, doua sisteme de vectori
concurenti:
. A calcula efectul mecanic produs in O de actiunea simultana a fortelor din sistemul dat
inseamna a reduce pe rand toate fortele sistemului, obtinand in O, doua sisteme de vectori
concurenti:
-sistemul
de forte ![]() ,
, ![]() ,..,
,.., ![]() , a carui rezultanta este:
, a carui rezultanta este:
![]() (2.24)
(2.24)
-sistemul
de cupluri ![]() ,
, ![]() ,..,
,.., ![]() , al carui moment rezultant este:
, al carui moment rezultant este:
![]() (2.25)
(2.25)
|
Fig. 2.12 |
Forta
rezultanta ![]() si momentul
rezultant
si momentul
rezultant ![]() formeaza un
sistem echivalent cu sistemul de forte dat, numit torsorul de reducere in punctul O.
formeaza un
sistem echivalent cu sistemul de forte dat, numit torsorul de reducere in punctul O.
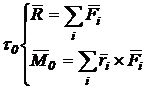 (2.26)
(2.26)
Reducand sistemul de forte intr-un alt punct O, se obtine:
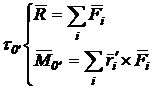 (2.27)
(2.27)
Expresia
momentului ![]() , tinand seama de relatia (2.4), devine:
, tinand seama de relatia (2.4), devine:
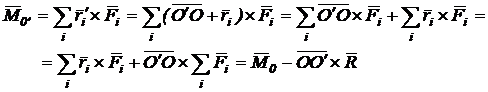 (2.28)
(2.28)
Torsorul in punctul O al sistemului de forte este:
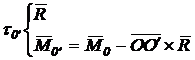 (2.29)
(2.29)
Comparand relatiile (2.26) si (2.27) se deduce ca in raport cu puncte diferite de reducere, rezultanta este aceasi, in timp ce momentul rezultant variaza, legea de variatie a acestuia fiind data de relatia (2.28).
Rezultanta ![]() este primul invariant
al operatiei de reducere
este primul invariant
al operatiei de reducere
Efectuand
produsul scalar ![]() , numit trinom
invariant si avand in vedere ca produsul mixt
, numit trinom
invariant si avand in vedere ca produsul mixt ![]() , fiind produs mixt cu vectori coplanari, obtinem:
, fiind produs mixt cu vectori coplanari, obtinem:
![]() (2.30)
(2.30)
Trinomul invariant ![]() este al doilea invariant al operatiei de
reducere.
este al doilea invariant al operatiei de
reducere.
Forma
analitica a trinomului invariant ![]() este:
este:
![]() (2.31)
(2.31)
Proiectia
momentului rezultant ![]() pe directia
rezultantei
pe directia
rezultantei ![]() este:
este:
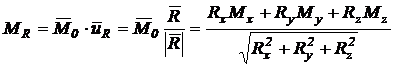 (2.32)
(2.32)
Vectorul
![]() , coliniar cu rezultanta
, coliniar cu rezultanta ![]() se va scrie:
se va scrie:
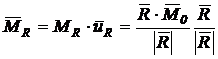 (2.33)
(2.33)
Proiectia
momentului rezultant pe directia rezultantei ![]() fiind raportul a
doua marimi invariante
fiind raportul a
doua marimi invariante ![]() si
si ![]() este in
consecinta, tot o marime invarianta a operatiei de
reducere (fig.2.12.b). Adica:
este in
consecinta, tot o marime invarianta a operatiei de
reducere (fig.2.12.b). Adica:
![]() (2.34)
(2.34)
Trinomul invariant si
proiectia momentului rezultant pe directia rezultantei nu sunt
doua marimi invariante independente. La reducerea intr-un punct a
unui sistem de forte exista doi invarianti, ![]() si
si ![]() .
.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1142
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved