| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Rezolvarea numerica a ecuatiilor diferentiale ordinare
Tematica lucrarii:
1. Generalitati;
2. Rezolvarea numerica a ecuatiilor diferentiale ordinare de ordinul intai;
3. Problema de rezolvat (1);
4. Rezolvarea numerica a sistemelor de ecuatii diferentiale ordinare;
5. Problema de rezolvat (2);
6. Concluzii.
1. Generalitati
O ecuatie diferentiala ordinara de ordinul n este o relatie matematica intre o functie reala u(t) de o singura variabila reala t si derivatele acesteia de diferite ordine, u', u', , u(n) corespunzator ordinului ecuatiei diferentiale. In continuare consideram ca argumentul functiei reprezinta timpul din modelul fizic al sistemului studiat si il notam cu t. Necunoscuta ecuatiei diferentiale este functia u(t).
u(t)(n) = F(t,u,u',u',,u(n-1) (1)
Derivata de ordinul unu reprezinta viteza de variatie a functiei, iar derivatele de ordine superioare reprezinta vitezele de variatie ale derivatelor de cu un ordin mai mic.
![]()
![]() (2)
(2)
Sistemele de ecuatii diferentiale sunt similare din punct de vedere formal daca sunt reprezentate vectorial. In acest caz functia devine functia vectoriala u(t), iar functionala F(t,u,u',u',,u(n-1)) devine functionala vectoriala F(t,u,u',u',,u(n-1)) , avand ca argumente functii vectoriale. Amintim ca o functionala este o aplicatie avand argument vectorial si valori scalare. Astfel un sistem de ecuatii diferentiale poate fi reprezentat in forma vectoriala compacta prin relatia:
u(t)(n) = F(t,u,u',u',,u(n-1) (3)
unde u(t) si F(t,u,u',u',,u(n-1)) au reprezentarea explicita urmatoare:
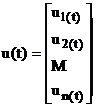
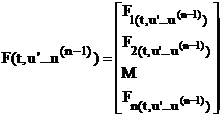 (4)
(4)
unde componentele u ,u ,,un sunt functii (scalare) reale de variabila reala, iar componentele F ,F ,,Fn sunt functionale (scalare) reale.
Este important faptul ca orice ecuatie de ordin n poate fi transformata intr-un sistem de ecuatii diferentiale de ordinul unu daca sunt utilizate ca necunoscute auxiliare derivatele de ordine superioare lui unu. Rezulta ca orice problema diferentiala de ordin superior (definita de o singura ecuatie sau de un sistem de ecuatii) poate fi transformata intr-o problema de ordinul unu. Pentru ca o ecuatie diferentiala (sau sistem de ecuatii diferentiale) sa aiba solutie unica este necesar ca aceasta sa fie completata cu o relatie reprezentand conditia initiala, adica valoarea solutiei la momentul initial. Acest ansamblu de ecuatii se numeste Problema Cauchy. In cazul ecuatiei diferentiale de ordinul unu problema Cauchy este descrisa de relatiile:
![]() (5)
(5)
u(t ) = u (6)
In cazul sistemului de ecuatii diferentiale de ordinul unu problema Cauchy este descrisa de relatiile:
![]() (7)
(7)
u(t ) = u (8)
unde u(t) si F(t,u(t)) reprezinta respectiv o functie si o functionala vectoriala.
2. Rezolvarea numerica a ecuatiilor diferentiale ordinare de ordinul intai
a) Metoda Euler
Metoda Euler este realizeaza o aproximatie de ordinul unu, adica aproximeaza variatia finctiei u(t) cu o variatie liniara. Metoda rezulta din aproximatia diferentialelor cu diferente finite de ordinul intai. Daca consideram ca variabila independenta t si functia u(t) au o variatie discreta indexata dupa k, rezulta relatia:
![]() (9)
(9)
unde cu uk am notat valoarea esantionului functiei necunoscute u(t) in punctul (momentul) tk, uk = u(tk) , iar cu f(tk,uk) valoarea functionalei F corespunzatoare valorilor tk si uk . Astfel se poate construi ecuatia recursiva pentru determinarea lui u(t), pas cu pas, pornind de la valoarea initiala data, unde cu h a fost notata valoarea corespunzatoare pasului de calcul:
b) Metoda Runge-Kutta
Metoda Runge-Kutta poate fi implementata pentru diferite ordine de aproximare. Astfel sunt realizate aproximatii care tin cont de derivatele pana la ordinul respectiv. Ecuatia recursiva a metodei Runge-Kutta de ordinul patru (in notatie MathCad), este urmatoarea:
![]() (11)
(11)
unde w1, w2, w3,si w4, reprezinta ponderi care pot fi definite ca functii de t si u(t) dupa cum urmeaza:
![]()
![]() (12)
(12)
![]()
![]() (13)
(13)
3. Problema de rezolvat (1)
Pentru aplicarea metodelor prezentate mai sus propunem rezolvarea problemei determinarii evolutiei curentului intr-un circuit rezistiv-inductiv, dupa conectarea la sursa de tensiune electromotoare alternativa. Utilizam urmatoarele notatii:
|
|
R - rezitenta circuitului;
L - inductivitatea circuitului;
e(t) - tensiunea de alimentare;
E - amplitudinea tensiunii de alimentare;
- pulsatia tensiunii de alimentare;
- faza tensiunii de alimentare;
i(t) - curentul prin circuit.
|
Fig. 1. Modelul circuitului electric |
Daca aplicam teorema lui Kirchhoff obtinem ecuatia de functionare a circuitului:
|
|
(14)
unde e(t) = Esin(t+ reprezinta variatia tensiunii de alimentare.
Daca separam derivata in membrul stang, iar membrul drept il definim ca o fuctionala dependenta de timp si curent rezulta ecuatia diferentiala:
![]() (15)
(15)
cu ajutorul careia se poate defini urmatoarea problema Cauchy:
![]() ; i(t ) = i (16)
; i(t ) = i (16)
In continuare se cere determinarea grafica a evolutiei curentului in intervalul [a,b] folosind mediul de programare MathCad luand utilizand ca date de intrare pentru circuitul electric valorile (conventionale) de mai jos. Se considera ca lucram in unitatile sistemului international. Pentru procesul de discretizare vom considera N = 50 de esantioane si un indice k luand valori de la 0 la N, definit sub forma unei variabile sir k := 0..N . Rezolvarea numerica se va face atat prin metoda Euler cat si prin metoda Runge-Kutta.
R = 1 ; L = 0.1 ; E = 1 ; (17)
= 0 ; i ; (18)
a = 0 ; b = 0.05 ; t ; (19)
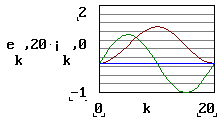 Fig.2
Evolutia curentului fata de evolutia t.e.m.
Fig.2
Evolutia curentului fata de evolutia t.e.m.
Se cere:
Scrierea in limbaj MathCad a procedurilor prezentate mai sus;
Realizarea procesului pas cu pas prezentat;
Trasarea graficului pentru solutia ecuatiei diferentiale;
Analiza erorilor pentru metodele prezentate, pentru diferite marimi ale pasului de calcul.
4. Rezolvarea numerica a sistemelor de ecuatii diferentiale ordinare
Rezolvarea numerica a sistemelor de ecuatii diferentiale ordinare este, din punct de vedere formal, asemanatoare cu rezolvarea ecuatiilor diferentiale ordinare. In cazul sistemelor, functia solutie si membrul drept al ecuatiei diferentiale reprezinta vectori.
In cazul metodei lui Euler ecuatia recursiva devine (in notatie MathCad):
u<k+1> := u<k> + h f(tk,u<k> (20)
unde u<k> si u<k+1> reprezinta vectorii functiei solutie la pasul k, respectiv la pasul k+1, iar f(tk,u<k>) reprezinta vectorul corespunzator membrului drept al ecuatiei diferentiale, evaluat la pasul k. Si in cazul sistemelor de ecuatii, h ramane o valoare scalara (numerica), reprezentand distanta pe care evolueaza solutia, in spatiul multidimensional respectiv, pe directia data de vectorul f(tk,u<k>
In cazul sistemelor de ecuatii diferentiale metoda Runge-Kutta se reprezinta la fel din punct de vedere formal, dar variabilele implicate au un caracter vectorial. Astfel la fiecare pas solutia este evaluata conform ecuatiei recursive:
![]() (21)
(21)
unde u<k> si u<k+1> reprezinta vectorii functiei solutie la pasul k, respectiv la pasul k+1, iar ponderile vectoriale w1, w2, w3, w4 au aceleasi formule de calcul ca mai sus, insa reprezentate vectorial.
5. Problema de rezolvat (2)
Se considera problema determinarii evolutiei in functie de timp a tensiunii si curentului pentru un circuit oscilant continand o inductanta L si o capacitate C.
 Fig. 3 Circuitul oscilant LC
Fig. 3 Circuitul oscilant LC
Conform relatiilor de definitie a celor doua componente de circuit, dependenta dintre tensiunea si curentul circuitului oscilant este exprimata prin relatiile:
![]()
![]() (22)
(22)
Daca separam in membrul stang derivatele, obtinem un sistem de ecuatii diferentiale caruia ii asociem o conditie initiala, pentru a asigura unicitatea solutiei. Tinand seama de faptul ca caderea de tensiune are sensuri opuse pentru inductanta si condensator (datorita modului de circulatie a curentului), atunci cand asociem ecuatiile in cadrul sistemului trebuie sa facem o schimbare de semn. Sa consideram prin conventie semnul tensiunii pe condensator pozitiv.
u(t) = uC(t) = - uL(t) (23)
![]() u(t ) = u (24)
u(t ) = u (24)
![]() i(t ) = i (25)
i(t ) = i (25)
Trebuie mentionat ca datorita faptului ca in circuit nu exista surse de energie, pentru a avea o solutie nenula este strict necesar ca conditia initiala sa fie nenula.
In continuare se cere determinarea grafica a evolutiei tensiunii si curentului in intervalul [a,b] folosind mediul de programare MathCad utilizand ca date de intrare pentru circuitul electric valorile (conventionale) de mai jos. Se considera ca lucram in unitatile sistemului international. Pentru procesul de discretizare vom considera N = 50 de esantioane, un indice k luand valori de la 0 la N si un pas de timp h = Rezolvarea numerica se va face atat prin metoda Euler cat si prin metoda Runge-Kutta. Prin reprezentarea pe acelasi grafic a celor doua legi de variatie sa se determine defazajul celor doua marimi.
Se vor considera datele cu valorile (cu caracter conventional) de mai jos:
L = 0.1 ; C = 10 (26)
u = 1 ; i (27)
Mentionam ca in cadrul programului MathCad indicele vectorial este reprezentat prin exponent plasat intre paranteze ascutite. Functionala din membrul drept al sistemului de ecuatii diferentiale, corespunzatoare unui anumit pas de calcul, poate fi definita ca o functie MathCad vectoriala in forma de mai jos:
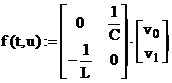 (28)
(28)
unde v si v reprezinta cele doua componente ale vectorului solutie, prima corespunzand tensiunii, iar cealalta curentului.
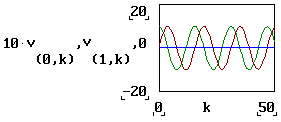
Fig.4 Evolutia curentului si tensiunii pe condensator
Observatie
Trebuie mentionat ca ordinul de aproximare al metodei este foarte important din punctul de vedere al erorilor obtinute la nivelul fiecarui pas de calcul. Astfel, daca este utilizata o metoda cu un ordin de aproximare superior, se pot alege pasi de calcul de lungime mai mare. Aceasta situatie este favorabila in cazul problemelor cu timpi lungi de evolutie, pentru care cumularea erorilor relative la pasul de calcul duce la o perturbatie importanta a solutiei. In figura 5 se poate observa solutia numerica calculata cu metoda Euler (metoda de ordinul unu) pentru evolutia tensiunii din problema de mai sus. Forma solutiei este mult diferita, datorita erorilor specifice metodei, desi s-a utilizat acelasi pas de calcul.
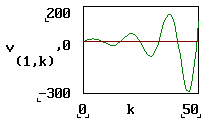 Fig.5 Solutie numerica
obtinuta prin metoda Euler
Fig.5 Solutie numerica
obtinuta prin metoda Euler
Se cere:
* Scrierea in limbaj MathCad a procedurilor prezentate mai sus;
* Realizarea procesului pas cu pas prezentat;
* Trasarea graficului pentru cele doua functii solutie ale sistemului de ecuatii diferentiale;
* Analiza erorilor pentru metodele prezentate, pentru diferite marimi ale pasului de calcul.
6. Concluzii
Ecuatiile diferentiale au ca necunoscuta o functie de o singura variabila. Prin rezolvarea numerica se obtin esantioanele acestei functii in cadrul unui anumit interval de variatie.
In cadrul metodei lui Euler variatia functiei solutie este aproximata la fiecare pas de calcul cu o variatie liniara (metoda de ordinul unu), iar in cadrul metodei Runge-Kutta variatia functiei este aproximata cu o curba de ordinul patru. Pentru exemplul numeric enuntat mai sus se observa ca metoda Runge-Kutta duce la o eroare mult mai redusa decat metoda Euler.
Alegerea pasului de calcul trebuie efectuata astfel incat, pentru un anumit interval de lucru eroarea cumulata sa se pastreze sub o anumita limita impusa.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2007
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved