| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Altermativa Fredholm
In acest paragraf vor fi mentionate
conditiile pe care trebuie sa le indeplineascaun operator liniar continuu T
care aplica spatiul Banach X in el insusi , pentru ca sa aiba loc alternativa
Fredholm. In particular se va vedea ca daca o putere ![]() a operatorului liniar U este operator compact , atunci pentru T = I -
U este valabila alternativa Fredholm. Rezultatele expuse mai jos apartin lui
S.M Nikolski
a operatorului liniar U este operator compact , atunci pentru T = I -
U este valabila alternativa Fredholm. Rezultatele expuse mai jos apartin lui
S.M Nikolski
1. Sa consideram ecuatia
![]()
si adjuncta ei
![]()
Vom considera de asemenea ecuatiile omogene corespunzatoare

Amintim ca valabilitatea alternativei Fredholm pentru operatorul T inseamna ca :
fie ecuatiile (1) si (2) au solutii pentru orice membru drept si atunci solutiile lor sunt unice
fie ecuatiile omogene (3) si (4) au
acelasi numar infinit de de solutii liniar independente ![]() respectiv
respectiv ![]() , in acest caz
pentru ca ecuatia (1) respectiv ecuatia (2) sa aiba solutie , este necesar si
suficient ca
, in acest caz
pentru ca ecuatia (1) respectiv ecuatia (2) sa aiba solutie , este necesar si
suficient ca
![]()
respectiv ca
![]()
In plus solutia generala a ecuatiei (1) este data de egalitatea
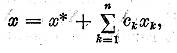
iar solutia generala a ecuatiei (2) de
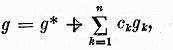
unde ![]() (respectiv
(respectiv ![]() ) este o solutie
oarecare a ecuatiei (1) iar
) este o solutie
oarecare a ecuatiei (1) iar ![]() sunt constante arbitrare
sunt constante arbitrare
Teorema urmatoare arata ca clasa operatorilor T pentru care are loc alternativa Fredholm se deosebeste in esenta putin de clasa operatorilor de forma T = I - U , unde U este operator compact.
Teorema 1. Fiecare din urmatoarele doua conditii este necesara si suficienta pentru ca alternativa Fredholm sa aiba loc pentru operatorul T.
1. Operatorul T poate fi reprezentat sub forma
![]()
unde operatorul W are invers bilateral continuu, iar operatorul V este compact.
2. Operatorul T poate fi reprezentat sub forma
![]()
unde operatorul ![]() are invers bilateral continuu, iar operatorul
are invers bilateral continuu, iar operatorul ![]() este finit dimensional.
este finit dimensional.
Demonstratie. Evident ne putem margini la demonstrarea suficientei conditiei 1) si necesitatii conditiei 2)
Suficienta conditiei 1) Fie
![]()
unde W are invers bilateral continuu, iar V este compact. Ecuatia (1) este echivalenta in acest caz cu ecuatia
![]()
Mai departe exista operatorul
invers bilateral ![]() de aceea ecuatia
(2) este echivalenta cu ecuatia
de aceea ecuatia
(2) este echivalenta cu ecuatia
![]()
in sensul ca daca ![]() este o solutie a ecuatiei(6) atunci
este o solutie a ecuatiei(6) atunci ![]() va fi solutie a
ecuatiei (2) iar daca
va fi solutie a
ecuatiei (2) iar daca ![]() va fi solutia ecuatiei (2) atunci
va fi solutia ecuatiei (2) atunci ![]() va fi solutia ecuatiei (6)
va fi solutia ecuatiei (6)
Sa
introducem notatia ![]() Tinand cont de
faptul ca
Tinand cont de
faptul ca ![]()
![]()
![]() putem reprezenta ecuatiile (5) si (6) sub
forma
putem reprezenta ecuatiile (5) si (6) sub
forma
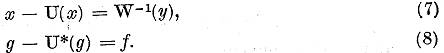
Deoarece operatorul U este compact pentru ecuatiile (7) si (8) este valabila concluzia teoremei 1.4. Prin urmare ecuatiile omogene

au acelasi numar(finit) de
solutii liniar independente ![]()
![]() Ecuatia omogena (3) va avea evident acelasi sistem complet de solutii liniar
independente ca si ecuatia (9) anume
Ecuatia omogena (3) va avea evident acelasi sistem complet de solutii liniar
independente ca si ecuatia (9) anume![]() . Sa demonstram ca
functionalele
. Sa demonstram ca
functionalele
![]()
formeaza un sistem complet de solutii liniar independente ale ecuatiei(4). Faptul ca fiecare din functionale(11) este solutia ecuatiei (4) rezulta dinechivalenta ecuatiilor (2) si (6) mentionate mai sus. Functionalele (11) sunt liniar independente deoarece relatia
![]()
rezulta
![]()
ceea ce este posibil doar daca ![]() In sfarsit daca
ecuatia (4) ar avea o solutie
In sfarsit daca
ecuatia (4) ar avea o solutie ![]() care sa nu fie combinatie liniara de
functionale (11) atunci functionala
care sa nu fie combinatie liniara de
functionale (11) atunci functionala ![]() ar fi o solutie a ecuatiei (10) care ar fi o
conbinatie liniara de functionale
ar fi o solutie a ecuatiei (10) care ar fi o
conbinatie liniara de functionale ![]() ceea ce nu ar fi posibil.
ceea ce nu ar fi posibil.
Astfel ecuatiile (3) si (4) au acelasi numar finit de solutii liniar independente . Apoi pe baza teoremei 1.4. ecuatia (5) si prin urmare si ecuatia (1) are solutie atunci si numai atunci cand
![]()
Aceasta conditie este echivalenta , in virtutea definitiei (11)
![]()
Analog se verifica faptul ca pentru solubilitatea ecuatiei (2) conditiile
![]()
sunt necesare si suficiente.
Necesitatea conditiei 2). Fie ![]() sisteme complete de solutii liniare
independente ale ecuasiilor (3) si (4). Folosind teoreme V.4.7. si lema
III.3.1. vom gasi functionalele
sisteme complete de solutii liniare
independente ale ecuasiilor (3) si (4). Folosind teoreme V.4.7. si lema
III.3.1. vom gasi functionalele ![]() si elementele
si elementele ![]()
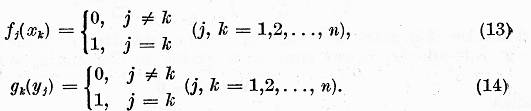
Sa notam ![]() Fiecare element
Fiecare element ![]() poate fi reprezentat unic sub forma
poate fi reprezentat unic sub forma
![]()
Intradevar daca punem
![]()
atunci in virtutea relatiei (14)
![]()
deci ecuatia ![]() are solutie si prin urmare
are solutie si prin urmare ![]() . Unicitatea reprezentarii (15) rezulta din
faptul ca daca
. Unicitatea reprezentarii (15) rezulta din
faptul ca daca
![]()
atunci ecuatia ![]() trebuie sa aiba solutie si de aceea
trebuie sa aiba solutie si de aceea ![]()
Sa notam acum ![]()
Se demonstreaza analog ca fiecare element ![]() poate fi reprezentat in mod unic sub forma
poate fi reprezentat in mod unic sub forma
![]()
Vom construi operatorul W punand
![]()
si vom demonstra ca W realizeaza o aplicatie bijectiva a spatiului X pe el insusi si prin urmare are un invers bilateral continuu
Pentru aceasta fie y un element arbitrar din X, ![]() reprezentarea lui sub forma (15). Aici
reprezentarea lui sub forma (15). Aici
![]()
adica ecuatia ![]()
![]() are o solutie
are o solutie ![]() care poate fi
considerata a fi un element din
care poate fi
considerata a fi un element din ![]()
Punand
![]()
si tinand cont ca ![]() si totodata de relatia (13) obtinem
si totodata de relatia (13) obtinem
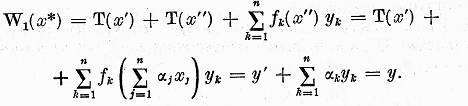
Sa aratam ca in afara de elementul x nu exista alte solutii ale ecuatiei ![]() y. Intradevar in
caz contrar ar exista un element
y. Intradevar in
caz contrar ar exista un element ![]() astfel ca
astfel ca
![]()
adica
![]()
Aici ![]() iar
iar
![]()
In virtutea unicitatii reprezentarii unui element sub forma (15) ajungem la relatiile
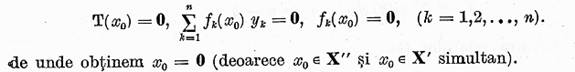
Pentru a incheia demonstratia teoremei este suficient sa definim
![]()
Observatie. Propunem cititorului sa demonstreze daca
operatorul T este inlocuit in conditiile 1) sau 2) prin operatorul ![]() se obtin doua conditii de asemenea necesare si
suficiente pentru ca alternativa Fredholm sa aiba loc pentru operatorul T .
se obtin doua conditii de asemenea necesare si
suficiente pentru ca alternativa Fredholm sa aiba loc pentru operatorul T .
2. Expunerea ulterioara se bazeaza pe 2 leme simple
Lema 1. Fie A si B doi operatori liniari continui care aplica spatiul narnat X in el insusi. Daca acesti operatori comuta iar operatorul C = AB are invers (bilateral ) atunci si operatorii A si B sunt inversabili
Demonstratie. Sa demonstram intai ca operatorii A si ![]() comuta, intradevar avem
comuta, intradevar avem
![]()
Inmultind aceasta relatie la dreapta cu ![]() obtinem
obtinem ![]() Mai departe folosind faptul demonstrat ca A si
Mai departe folosind faptul demonstrat ca A si
![]() comuta putem scrie
comuta putem scrie
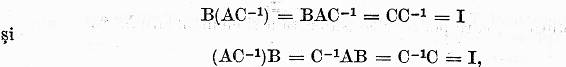
de unde rezulta ca exista ![]() Analog se demonstreaza ca exista
Analog se demonstreaza ca exista ![]()
Observatie. Daca operatorul ![]() este continuu atunci si operatorii
este continuu atunci si operatorii ![]() si
si ![]() vor fi continui.
vor fi continui.
Lema 2. Fie U un operator continuu in spatiul X . Multimea
caracteristica ![]() a operatorului U si multimea caracteristica
a operatorului U si multimea caracteristica ![]() a operatorului
a operatorului ![]() sunt legate prin relatia
sunt legate prin relatia
![]()
adica daca, ![]()
Demonstratie. Sa notam ![]() Avem
Avem
![]()
Daca 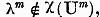 atunci punand
atunci punand
![]()
rezulta ca exista inversul continuu ![]() Prin urmare pe baza observatiei la teorema 1
exista inversul continuu
Prin urmare pe baza observatiei la teorema 1
exista inversul continuu ![]()
3. Presupunand ca X este spatiul Banach , ca in sectiunea 1. sa consideram un operator liniar continuu U in X .
Teorema 2. Sa presupunem ca emista un numar natural m astfel
incat operatorul ![]() sa fie compact. Atunci pentru operatorul
sa fie compact. Atunci pentru operatorul 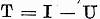 este valabila alternativa Fredholm.
este valabila alternativa Fredholm.
Demonstrasie. Conform lemei 2 multimea caracteristica ![]() consta din puncte izolate, de aceea pe cercul
unitate al planului complex se afla doar un numar finit de puncte
consta din puncte izolate, de aceea pe cercul
unitate al planului complex se afla doar un numar finit de puncte ![]()
Daca p parcurge multimea tuturor numerelor prime numerele
![]()
sunt distincte si de aceea pentru ![]() suficient de mare
suficient de mare
![]()
Se poate presupune ca m este un numar prim si ca ![]() . Sa scriem
descompunerea
. Sa scriem
descompunerea
![]()
unde
![]()
Ca urmare a relatiei (17) operatorii ![]() sunt inversabili si prin urmare exista
operatorul continuu
sunt inversabili si prin urmare exista
operatorul continuu ![]() Dar atunci
Dar atunci
![]()
Deoarece operatorul ![]() este inversabil iar operatorul
este inversabil iar operatorul ![]() este compact se poate aplica teorema 1 .
este compact se poate aplica teorema 1 .
Teorema este demonstrata
4. Teorema asupra multimii caracteristice a unui operator compact se extinde la operatorii de forma considerata in teorema anterioara . Anume are loc
Teorema 3. Daca pentru un m oarecare operatorul ![]() este compact atunci
este compact atunci
1) multimea caracteristica ![]() a operatorului U consta numai din valori
caracteristice iar fiecare valoare caracteristica are rang finit si subspatiul propriu corespunzator este
finit dimensional ; 2) in fiecare disc
a operatorului U consta numai din valori
caracteristice iar fiecare valoare caracteristica are rang finit si subspatiul propriu corespunzator este
finit dimensional ; 2) in fiecare disc ![]() al planului complex se afla numai un numar finit de valori
caracteristice
al planului complex se afla numai un numar finit de valori
caracteristice
Demonstratie. Tinand seama de rezultatul lemei 2 ne putem limita la demonstrarea primului punct al teoremei. In plus prima parte rezulta in mod evident din teorema 2. Prin urmare ramane de demonstrat doar finitudinea dimensiunii subspatiului propriu corespunzator.
Fara a se restrange generalitatea se poate presupune ca valoarea proprie
considerata este ![]() Pe baza dezvoltarii (18) se poate scrie
Pe baza dezvoltarii (18) se poate scrie
![]()
Deoarece operatorii ![]() comuta intrei ei avem
comuta intrei ei avem
![]()
De aici rezulta ca
![]()
Astfel deoarece ![]() este operator compact si tinand seama ca
pentru astfel de operatori afirmatia a fost deja stabilita putem conchide pe baza relatiei (19) ca
aceasta afirmatie este valabila si in cazul considerat.
este operator compact si tinand seama ca
pentru astfel de operatori afirmatia a fost deja stabilita putem conchide pe baza relatiei (19) ca
aceasta afirmatie este valabila si in cazul considerat.
In incheiere sa dam un exemplu de operator liniar continuu U
care nu este compact dar ![]() este compact.
este compact.
Fie X unul din spatiile![]() Pentru
Pentru ![]() sa punem
sa punem ![]()
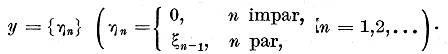
Evident ![]()
Observatie. Intrucat teoremele din cap. 4 demonstrate pentru operatorii comnacti, au folosit doar acele proprietati ale operatorilor compacti care sunt incluse in teorema 1.1. si teorema 3.1. iar acele teoreme se extind fara modoficatie la cazul operatorilor de forma considerata mai sus, rezultatele mentionate sunt de asemenea adevarate daca se presupune doar ca o anumita parte a operatorului U este compacta.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1343
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved