| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
In continuare, vom evalua complexitatea problemelor computationale din punctul de vedere al spatiului (sau memoriei) pe care il folosesc.
Motivul: timpul si spatiul sunt doi dintre cei mai importanti parametri care trebuie luati in considerare atunci cand se cauta solutii efective pentru cele mai multe dintre problemele de calcul.
Desi complexitatea spatiu seamana in multe privinte cu complexitatea timp, ea ofera posibilitati noi de clasificare a problemelor din punctul de vedere al complexitatii lor computationale.
Si in cazul complexitatii spatiu este necesar un model de calculabilitate (care sa permita masurarea spatiului folosit de un algoritm). Vom utiliza tot modelul masinii Turing pentru ca este simplu din punct de vedere matematic si foarte apropiat de calculatorul real.
1. Definitie
(i) Fie M o MT determinista care se opreste, oricare ar fi secventa pe care o primeste pe banda de intrare.
Se numeste complexitatea spatiu determinist a M o functie
f : N N f(n) = numarul maxim de locatii de pe banda de intrare pe care le scaneaza M atunci cand primeste o secventa de intrare de lungime n, ( )nIN
Mai spunem ca M ruleaza intr-un spatiu de memorie egal cu f(n).
(ii) Fie M o MT nedeterminista in care oricare dintre ramurile calculului nedeterminist se opreste, oricare ar fi secventa pe care o primeste pe banda de intrare.
Se numeste complexitatea spatiu nedeterminist a M o functie
f : N N , f(n) = numarul maxim de locatii de pe banda de intrare pe care le scaneaza M de-a lungul oricareia dintre ramurile de calcul atunci cand primeste o secventa de intrare oarecare, de lungime n, ( ) nIN
2. Observatie
Vom estima complexitatea spatiu a masinilor Turing tot cu ajutorul notatiei asimptotice.
3. Definitie
Fie f :
SPACE(f(n)) =
NSPACE(f(n))
4. Exemple
Una dintre cele mai cunoscute probleme NP-complete este SAT (problema evaluarii: satisfiability problem). Am afirmat ca SAT nu poate fi rezolvata cu un algoritm cu timp de lucru polinomial (si cu atat mai putin cu un algoritm cu timp de lucru linear).
Vom da aici un algoritm pentru rezolvarea SAT cu spatiu linear. O justificare: spre deosebire de timp, spatiul poate fi refolosit T resursa spatiu pare sa fie mai puternica decat resursa timp.
Definim urmatoarea MT determinista cu o singura banda:
M = "Fie secventa de intrare < f >, unde f este o formula booleeana oarecare:
1. Pentru fiecare combinatie de valori de adevar atribuite variabilelor booleene
x , x , . , xm din f
2. Se evalueaza valoarea de adevar a formulei f
3. Daca f se evalueaza la 1, atunci M accepta secventa de intrare; altfel, respinge."
Observam ca la fiecare iteratie a etapei a doua M1 utilizeaza aceeasi portiune a benzii de intrare pentru ca M1 trebuie sa memoreze numai combinatia curenta de valori de adevar ale variabilelor x , x , . , xm T spatiul necesar este de ordinul O(m). Cum numarul de variabile m este mariginit superior de n (adica de lungimea secventei de intrare, in care unele variabile se pot repeta!), inseamna ca M ruleaza in spatiu de ordinul O(n).
Ilustram complexitatea spatiu nedeterminista a unui limbaj, tratand o"complementara" a problemei limbajului vid: problema limbajului universal:
Fie un automat finit nedeterminist (AFN) A . Vrem sa verificam daca el accepta toate secventele din S*. Codificam aceasta problema prin urmatorul limbaj
ALLAFN
Ideea solutiei
Construim un
algoritm nedeterminist cu spatiu linear, N, care sa decida
asupra complementarei acestui limbaj, ![]() astfel:
astfel:
se utilizeaza nedeterminismul pentru a "ghici" o secventa respinsa de AFN;
se utilizeaza un spatiu de lucru linear pentru a tine evidenta starilor prin care poate trece AFN la diferite momente de timp;
Observam ca nu se stie daca ![]() I NP sau
I NP sau ![]() I coNP
I coNP
Solutie
N = "Fie secventa de intrare <A>, unde A este un AFN:
1. Se marcheaza starea initiala a lui A.
2. Se repeta etapa a treia de 2q ori, unde q = numarul de stari ale A (vezi definitia functiei de tranzitie a lui A !).
3. Se selecteaza nedeterminist un simbol de intrare si se remarcheaza starile lui A pentru a simula citirea acelui simbol.
4. Daca in etapele 2 si 3 apare o secventa pe care A o respinge (adica daca la un moment dat nici una dintre starile de acceptare ale lui A nu este marcata) atunci N accepta secventa de intrare <A>; altfel o respinge."
Daca exista secvente din S* pe care A le respinge atunci printre ele trebuie
sa se afle una de lungime cel mult 2q , deoarece in cazul tuturor secventelor de lungime
mai mare, respinse de A, locatiile markerilor descrisi in
algoritmul de mai sus ar trebui sa se repete (A are prin ipoteza
doar q stari). Portiunea din secventa cuprinsa intre
repetitii poate fi eliminata pentru a se obtine astfel o
secventa respinsa, mai scurta. Prin urmare, N decide asupra limbajului ![]() . (Se
observa ca N accepta si secvente de intrare
incorect formate.)
. (Se
observa ca N accepta si secvente de intrare
incorect formate.)
Acest algoritm necesita spatiu de memorie suplimentar numai pentru stocarea locatiilor markerilor si a contorului de ciclare, deci necesita spatiu linear. Prin urmare, algoritmul ruleaza in spatiu nedeterminist de ordinul O(n).
Urmatoarea teorema ofera informatii despre complexitatea spatiu determinist a limbajului ALLAFN.
Acesta este unul dintre primele rezultate privind complexitatea spatiu. El arata ca MT deterministe (prescurtat MTD) pot simula MT nedeterministe (prescurtat: MTN) utilizand o cantitate de memorie surprinzator de mica. Daca din punct de vedere al complexitatii timp o astfel de simulare pare sa necesite un timp de lucru exponential, din punct de vedere al complexitatii spatiu cresterea este - conform Teoremei Savitch - de la ordinul f(n) (spatiul necesitat de MTN) la ordinul f (n) (spatiul necesitat de MTD).
Teorema lui SAVITCH
Fie o functie f: N R+ cu proprietatea: f(n) n
T NSPACE (f(n)) SPACE (f (n))
Demonstratie
Ideea demonstratiei
Pentru a simula o MTN cu spatiu de lucru de ordinul f(n) in mod determinist am putea incerca sa verificam, una cate una, ramurile de calcul ale acelei MTN. Simularea trebuie sa marcheze ramura curent prelucrata pentru a putea trece la prelucrarea ramurii urmatoare. Fiecare dintre aceste ramuri de calcul (care utilizeaza f(n) locatii de pe banda de intrare) poate executa un numar de pasi de ordinul 2O(f(n)) (vezi definitia functiei de tranzitie a lui MTN !) iar fiecare pas ar putea fi ales in mod nedeterminist.
T Examinarea secventiala a ramurilor de calcul ar necesita - pentru fiecare ramura - memorarea pasilor executati T ar fi nevoie de 2O(f(n)) locatii de memorie, deci mult mai mult decat O(f (n))!
T Este necesara o alta abordare: vom rezolva o problema mai generala, numita
PROBLEMA TRANZITIEI[1]: fie doua configuratii c = uaqrbv si c = zcqsdw (a,b,c,dIG , nu neaparat distincte; u,v,z,w I G , nu neaparat distincte; qr, qs I Q) ale unei MTN si un numar t I N; trebuie sa verificam daca MTN poate trece din configuratia c in configuratia c in t pasi.
T Rezolvand PROBLEMA TRANZITIEI pentru
o c = configuratia de start a MTN;
o c = configuratia de acceptare a MTN;
o t = numarul maxim de pasi pe care ii poate face MTN.
putem verifica daca MTN accepta secventa de intrare primita.
Vom prezenta un algoritm determinist recursiv care rezolva PROBLEMA TRANZITIEI. Acest algoritm:
cauta o configuratie intermediara cm
verifica recursiv daca
o c trece in cm in t/2 pasi,
o cm trece in c in t/2 pasi.
Reutilizarea spatiului necesar fiecareia dintre cele doua verificari recursive permite o economie de spatiu semnificativa.
Acest algoritm are nevoie de spatiu pentru a memora informatia din stiva recursiva. Fiecare nivel al recurentei utilizeaza pentru memorarea unei configuratii un numar de locatii de memorie de ordinul O(f(n)). Adancimea recurentei este log(t), unde t = timpul maxim utilizat de MTN pe o ramura oarecare de calcul. Stim ca
t = 2O(f(n)) T log(t) = O(f(n))
T simularea determinista necesita O(f (n)) locatii de memorie.
Formalizare
Fie N o MTN care decide asupra limbajului L in spatiu f(n). Construim o MTD M care sa decida asupra limbajului L. Masina M va utiliza o procedura, TRANZ, care verifica daca o configuratie oarecare a lui N poate produce o alta configuratie intr-un anumit numar de pasi. Aceasta procedura rezova PROBLEMA TRANZITIEI descrisa mai sus.
(i) Definim procedura TRANZ
Fie w secventa de intrare primita de N,
t I N (pentru simplificare, putem presupune ca t este o putere a lui 2),
c , c doua configuratii oarecare ale N;
atunci, TRANZ(c , c , t) accepta daca N poate trece din configuratia c in configuratia c printr-un calcul nedeterminist cu maximum t pasi; altfel respinge.
TRANZ = "Fie datele de intrare c , c si t, ca mai sus:
1. Daca t = 1 atunci se verifica direct daca c = c2 sau daca c trece in c2 intr-un singur pas conform functiei de tranzitie a lui N.
Daca oricare dintre cele doua conditii este indeplinita atunci TRANZ accepta; daca nici una dintre conditii nu e indeplinita atunci TRANZ respinge.
2. Daca t > 1 atunci urmatoarele instructiuni se executa pentru fiecare configuratie cm a lui N pe intrarea w si cu spatiu de lucru f(n):
Se ruleaza TRANZ(c1, cm, t/2).
Se ruleaza TRANZ(cm, c2, t/2).
Daca pasii 3 si 4 se incheie ambii cu acceptare, atunci TRANZ accepta, altfel se continua cu o noua configuratie cm
6. Daca, pentru fiecare configuratie cm, cel putin unul dintre pasii 3 sau 4 se incheie cu respingere atunci TRANZ respinge."
(ii) Definim o MTD M care simuleaza N astfel:
mai intai modificam N astfel incat atunci cand N accepta, N isi goleste banda de intrare si isi deplaseaza cursorul in celula cea mai din stanga, intrand astfel intr-o configuratie numita caccept
notam cu cstart configuratia de start a lui N pe intrarea w ;
alegem o constanta d I N cu proprietatea ca N are maximum 2df(n) configuratii care utilizeaza f(n) locatii pe banda de intrare, unde n = |w|. Ca urmare, 2df(n) este o limita superioara pentru timpul de lucru al oricarei ramuri de calcul a lui N pe intrarea w.
M = "Fie cuvantul de intrare w:
1. Furnizeaza rezultatul produs de TRANZ(cstart, caccept df(n)
Justificare
Evident, algoritmul TRANZ rezolva PROBLEMA TRANZITIEI si, prin urmare, M simuleaza corect N. Mai trebuie sa demonstram ca M lucreaza cu spatiu O(f2(n)).
La fiecare apel recursiv al TRANZ, procedura memoreaza in stiva numarul de ordine al pasului de calcul curent precum si valorile lui c , c si t pentru a le putea restaura la revenirea din apelul recursiv. Ca atare, fiecare nivel de recurenta utilizeaza un spatiu de lucru suplimentar de ordinul O(f(n)). In plus, fiecare nivel de recurenta reduce dimensiunea lui t la jumatate. Initial, t = 2df(n) T adancimea recurentei este O(log 2df(n)) sau O(f(n)) T spatiul de memorie total este O(f2(n)).
In justificarea de mai sus apare o dificultate tehnica: atunci cand apeleaza procedura TRANZ, algoritmul M trebuie sa cunoasca valoarea lui f(n). Solutia consta in modificarea lui M astfel incat M sa incerce pe rand diverse valori pentru f(n): f(n) = 1, 2, 3, .Pentru fiecare valoare f(n) = i algoritmul M modificat utilizeaza TRANZ pentru a verifica daca se poate ajunge in configuratia de acceptare. De asemenea, M utilizeaza procedura TRANZ pentru a verifica daca N foloseste cel putin (i+1) locatii, astfel:
fie f(n) = i; algoritmul M modificat utilizeaza procedura TRANZ pentru a verifica daca N poate ajunge din configuratia de start in una dintre configuratiile de lungime i+1:
daca nici una dintre configuratiile de lungime i+1 nu este atinsa atunci M respinge;
daca este atinsa una dintre configuratiile de lungime i+1 si aceasta este o configuratie de acceptare atunci M accepta;
daca este atinsa una dintre configuratiile de lungime i+1 si aceasta nu este o configuratie de acceptare atunci M continua cu f(n) = i+1.
q.e.d.
6. Observatie
Teorema este adevarata si pentru functii f: N R+ cu proprietatea: f(n) log(n).
Aceasta clasa este analogul pentru complexitatea spatiu al clasei P , relative la complexitatea timp.
7. Definitie
Notam cu PSPACE clasa limbajelor decidabile in spatiu polinomial de catre MT deterministe cu o singura banda de intrare:
![]()
Notam cu NPSPACE clasa limbajelor decidabile in spatiu polinomial de catre MT nedeterministe cu o singura banda de intrare:
![]()
8. Corolar
PSPACE = NPSPACE
Demonstratie
Rezulta din Teorema lui Savitch si din faptul ca patratul unui polinom este inca un polinom.
9. Observatie importanta
Spre deosebire de complexitatea timp, unde problema P = NP este deschisa, aici, avem: PSPACE = NPSPACE.
Conform exemplelor 4: SAT I SPACE(n) si ALLAFN I coNSPACE(n) Conform Teoremei Savitch, ALLAFN I SPACE(n deoarece clasele de complexitate spatiu determinist sunt inchise la complementara. Prin urmare, ambele limbaje sunt in clasa PSPACE.
10. Conjectura privind relatia dintre diferitele clase de complexitate timp si spatiu
(i) P PSPACE
Fie functia t: N N, t(n) n, ( ) n I N orice MT care ruleaza in timp t(n) poate utiliza cel mult t(n) celule de pe banda de intrare deoarece la fiecare pas de calcul ea nu poate examina decat cel mult o celula.
(ii) NP PSPACE
Cu un rationament analog rezulta ca NP NPSPACE Aplicand Observatia 8 obtinem: NP PSPACE
(iii) Reciproc, putem gasi o majorare pentru complexitatea timp a unei MT in functie de complexitatea spatiu.
Stim ca o configuratie a unui automat (AFD, ., MT) consta dintr-o stare, o combinatie de simboluri de intrare (secventa de intrare de o anumita lungime, n) si, eventual, pozitia cursorului pe banda. Se demonstreaza ca un automat linear marginit (ALM) cu q stari care citeste un cuvant de lungime n de pe banda de intrare si care dispune de un alfabet de intrare S cu s elemente poate avea cel mult q n sn configuratii distincte.
Daca generalizam acest rezultat anterior rezulta imediat ca o MT care utilizeaza f(n) locatii de memorie, unde f(n) n, este o functie definita pe N cu valori in N, poate avea cel mult f(n) O(f(n)) configuratii distincte.
Am presupus ca MT se opreste indiferent de secventa de intrare primita T ea nu poate repeta o configuratie de mai multe ori
T o MT care utilizeaza f(n) locatii de memorie trebuie sa execute f(n) O(f(n)) pasi de calcul, deci:
![]()
Din (i), (ii) si (iii) rezulta ca:
NP PSPACE = NPSPACE EXPTIME
P PSPACE = NPSPACE EXPTIME
11. Observatie
Nu se stie inca daca vreuna dintre incluziuni nu este de fapt chiar o egalitate. S-ar putea descoperi oricand o simulare asemanatoare celei din demonstratia Teoremei lui Savitch care sa permita fuzionarea unora dintre aceste clase intr-o singura clasa.
Pe de alta parte, se demonstreaza ca P EXPTIME (Capitol 9) T cel putin una dintre incluziunile de mai sus este stricta dar nu se stie care!! In fapt, cei mai multi cercetatori cred ca toate incluziunile sunt stricte, adica accepta diagrama de mai jos ca descriind cel mai corect relatia dintre clasele de complexitate timp si spatiu:
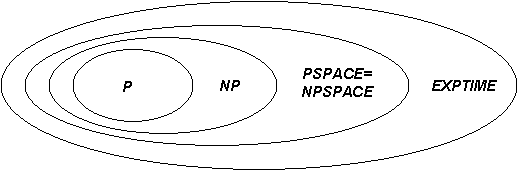
Am studiat problemele NP-complete si am aratat ca ele reprezinta categoria celor mai dificile limbaje din clasa NP . Daca o problema este NP-completa atunci este destul de sigur ca ea nu este in clasa P (daca ar fi, atunci clasele P si NP ar fi egale).
Introducem o notiune similara NP-completitudinii, dar pentru clasa PSPACE: PSPACE-completitudinea.
12. Definitie
Un limbaj B este PSPACE-complet daca si numai daca satisface urmatoarele doua conditii:
(1) B I PSPACE
) A I PSPACE T A P B (A este polinomial reductibil la B)
Daca limbajul B satisface numai conditia (2) atunci spunem ca el este PSPACE-dificil (PSPACE-hard).
13. Observatie
Motivul pentru care definim PSPACE-completitudinea tot in termenii reductibilitatii in timp polinomial este legat de esenta definitiei problemelor complete: Problemele complete sunt importante pentru ca ele sunt exemple de probleme dintre cele mai dificile din clasa lor de complexitate. O problema completa este foarte dificila pentru ca orice alta problema din clasa respectiva se poate reduce usor la ea astfel incat, daca gasim o meotda simpla de a rezolva problema completa atunci vom putea rezolva usor toate celelalte probleme din clasa respectiva. Pentru ca acest rationament sa fie valabil, este necesar ca reducerea sa fie simpla in raport cu tipul de complexitate a problemelor specifice clasei. T Regula este: oridecateori definim probleme complete pentru o anumita clasa de complexitate, modelul de reductibilitate trebuie sa fie mai limitat decat modelul folosit pentru a defini clasa insasi.
14. Definitie
O formula booleeana complet cuantificata (numita si propozitie) este o formula booleeana in care fiecare variabila este cuantificata.
1 Exemplu
f )x ( )y [(x y) x y)] este o formula booleeana complet cuantificata.
16. Definitie
Problema TQBF consta in verificarea valorii de adevar a unei formule booleene complet cuantificata (a unei propozitii) oarecare si este formalizata prin limbajul:
TQBF
17. Teorema
TQBF este o problema PSPACE-completa.
Ideea demonstratiei
Pentru a demonstra ca TQBF I PSPACE construim un algoritm care asigneaza valori de adevar variabilelor din formula si apoi evalueaza recursiv valoarea de adevar a acesteia. Pe baza acestei informatii, algoritmul poate determina daca formula data este sau nu adevarata.
pentru a arata ca toate limbajele L din PSPACE se reduc polinomial la TQBF
o construim mai intai pentru L o MT cu spatiu de lucru marginit polinomial;
o construim apoi o reducere polinomiala care asociaza unei secvente o formula booleeana cuantificata f care codifica o simulare a MT pe acea intrare ,
Formula este adevarata MT accepta.
Fie o formula booleeana complet cuantificata f )x1( )x2( )x3 . ( )xk [y
consideram un joc la care participa doi jucatori, E si U , care asigneaza pe rand valori de adevar variabilelor x1, x2, x3, . ,xk astfel incat E asigneaza valori variabilelor cuantificate existential iar U asigneaza valori variabilelor cuantificate universal. Daca prin aceasta asignare formula y se evalueaza la TRUE atunci castiga jucatorul E ; altfel castiga jucatorul U . Spunem ca jucatorul E are o strategie castigatoare pentru formula f daca - indiferent de asignarile facute de jucatorul U - jucatorul E poate asigna valori de adevar varibilelor (legate prin cuantificatori existentiali) in asa fel incat sa castige. Este evident ca jucatorul E are o startegie castigatoare pentru f daca si numai daca f se evalueaza la valoarea 1. Avem astfel:
18. Teorema
Limbajul
Formula-joc
este PSPACE-complet
(2) Sa consideram acum un alt joc, numit jocul geografic sau Antakhshari, relativ la numele oraselor. El poate fi modelat printr-o problema de grafuri orientate:
fiecare nod din digraf este etichetat cu numele unui oras
exista un arc de la nodul u la nodul v daca ultima litera a etichetei nodului u coincide cu prima litera a etichetei nodului v.
Jocul incepe intr-un nod oarecare, fixat; cei doi jucatori se deplaseaza alternativ in digraf, de-a lungul arcelor, in noduri nevizitate inca. Jucatorul care nu reuseste sa faca o noua deplasare pierde. Jocul poate fi generalizat la un digraf arbitrar (in care nodurile si arcele nu mai au nici o legatura cu orasele sau literele) si un nod predeterminat. Problema consta in a determina daca primul jucator are o strategie castigatoare. Avem astfel:
19. Teorema
Limbajul
Joc-geografic
este PSPACE-complet.
Ideea demonstratiei
Pentru a demonstra teorema ar trebui sa gasim o reducere in timp polinomial a problemei Formula-joc la problema Joc-geografic. Intrucat se crede ca P PSPACE este de presupus ca nu exista nici un algoritm cu timp de lucru polinomial care sa-i permita primului jucator sa verifice existenta unei strategii castigatoare, cu atat mai putin sa o determine.
In capitolele anterioare am analizat probleme a caror complexitate (timp sau spatiu) este cel putin lineara; in continuare examinam limite sublineare ale complexitatii:
limita sublineara pentru complexitatea timp este insuficienta pentru citirea datelor de intrare, deci nu ne ocupam de aceasta;
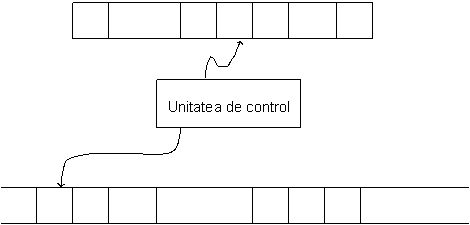
limita sublineara pentru complexitatea spatiu permite MT respective sa citeasca intreaga secventa de intrare dar nu ii permite sa o memoreze pe banda de intrare T pentru a cerceta eficient aceasta situatie trebuie schimbat modelul de calculabilitate T
20. Definitie
o banda de intrare, finita, de tip read-only, pe care se afla permanent secventa de intrare si numai ea;
o banda de lucru infinita de tip read/write, obisnuita.
o pe banda de intrare cursorul poate doar citi simbolurile dar nu poate scrie (vom introduce o conventie pentru a determina situatia in care cursorul a ajuns in extremitatea stanga / dreapta a benzii de intrare deoarece el trebuie sa ramana permanent numai pe portiunea benzii care contine informatie);
o pe banda de lucru cursorul poate citi si/sau scrie simboluri in mod normal.
T numai celulele scanate de cursor pe banda de lucru determina complexitatea spatiu a acestui tip de MT.
![]() 21 Definitie
21 Definitie
Fie M o MT dotata cu o banda de intrare separata de tip read-only;
cuvantul de intrare w I S
T o configuratie a lui M pentru intrarea w trebuie sa descrie:
starea masinii,
secventa de pe banda de lucru si
prozitiile celor doua cursoare.
De remarcat faptul ca secventa w de pe banda de intrare nu face parte din configuratie; motivul: banda de intrare contine - neschimbata, pe parcursul intregului calcul - tocmai secventa w.
22. Observatie
Putem asimila aceasta MT cu spatiu sublinear cu un calculator a carui memorie principala este destul de mica dar care totusi poate manipula cantitati mult mai mari de date (stocate de exemplu pe un CD-ROM, DVD etc.) fara a le depune complet in memoria principala.
23. Observatie
Daca spatiul de lucru al acestei MT cu 2 benzi este de ordin cel putin linear atunci ea este echivalenta cu o MT standard. Pentru spatiu de lucru de ordin sublinear nu putem utiliza ca model de calcul decat MT cu doua benzi descrisa mai sus.
Fie M o MT cu spatiu logaritmic (conform Definitiei 22) , marginit de o functie f(n). T
(1) numarul configuratiilor lui M pentru o secventa de intrare de lungime n este de cel mult n O(f(n))
(2) daca f(n) log n atunci acest numar este de 2O(f(n))
Demonstratie[6]
(1) Sa presupunem ca M are s stari si b simboluri in alfabetul benzii. T numarul de cuvinte care pot aparea pe banda de lucru este bf(n)
Cursorul benzii de intrare poate avea n pozitii iar cel al benzii de lucru f(n) pozitii.
T numarul total de configuratii ale M pentru w , care este o limita superioara pentru timpul de calcul al M pentru w , este s n f(n) bf(n), sau n O(f(n))
(2) rezulta imediat din (1) si din ipoteza f(n) log n. q.e.d.
Tratam ordinul de complexitate log n (in loc de ![]() sau log n) deoarece spatiul logaritmic
este suficient de mare pentru a stoca pointeri catre secventa de
intrare ceea ce permite rezolvarea unor probleme computatioanle interesante. In
plus, spatiul logaritmic are proprietati matematice remarcabile
(precum robustetea). Clasele N si NL , si mai exact algoritmii de reducere cu spatiu logaritmic sunt
foarte utili atunci cand trebuie sa facem distinctie intre diferitele
probleme "usoare", cum sunt cele din clasa P .
sau log n) deoarece spatiul logaritmic
este suficient de mare pentru a stoca pointeri catre secventa de
intrare ceea ce permite rezolvarea unor probleme computatioanle interesante. In
plus, spatiul logaritmic are proprietati matematice remarcabile
(precum robustetea). Clasele N si NL , si mai exact algoritmii de reducere cu spatiu logaritmic sunt
foarte utili atunci cand trebuie sa facem distinctie intre diferitele
probleme "usoare", cum sunt cele din clasa P .
25 Definitie
Notam cu L clasa limbajelor decidabile de catre o MT determinista in spatiu de lucru logaritmic:
L = SPACE(log n)
Notam cu NL clasa limbajelor decidabile de catre o MT nedeterminista in spatiu de lucru logaritmic:
NL = NSPACE(log n)
Limbajul L | k I L
Asa cum am aratat mai sus, o MT cu 2 benzi care primeste la intrare un cuvant w I * incepe prin a verifica daca w are forma corecta; aceasta etapa a algoritmului nu necesita spatiu suplimentar. Daca w este corect format, adica w = 0k h numerele k si h sunt memorate pe banda de lucru si comparate unul cu celalalt. Cum k si h pot fi memorate pe banda in format binar utilizand O(log n) biti, rezulta ca banda de lucru utilizeaza un spatiu de lucru de ordin algoritmic.
Limbajul PATH = I NL
Am demonstrat ca PATH I P ; nu stim daca PATH I L. Putem insa construi o MTN care sa exporeze nedeterminist drumurile de lungime cel mult m (m = numarul de noduri din G) si care sa accepte secventa de intrare <G,s,t> daca si numai daca nodul t poate fi atins din s. Intrucat la fiecare pas de calcul este suficient sa memoram numai nodul curent de pe drumul curent cercetat, rezulta ca PATH I NL
27. Observatie[8]
Am aratat
ca orice MT cu spatiu de
lucru f(n) ruleaza in timp cel mult 2O(f(n)). Aceasta proprietate nu
mai este adevarata pentru MT
cu spatiu de lucru de mici dimensiuni: de exemplu, o MT care ruleaza cu
spatiu de lucru O(1) (adica o
28. Observatie
Teorema lui Savitch demonstreaza faptul ca transformarea unei MTN intr-o MTD determina o crestere a complexitatii spatiu de la f(n) doar la f (n), daca f(n) n. Putem generaliza Teorema lui Savitch si la MT cu spatiu sublinear de tip f(n) log n. Demonstratia este similara celei initiale dar cu doua deosebiri:
se foloseste o MT cu spatiu logaritmic (vezi Definitia 20);
in locul configuratiilor MTN N se utilizeaza configuratii ale N pentru w .
Memorarea unei configuratii a lui N pentru w necesita
log(n O(f(n))) = log n + O(f(n)) locatii.
Daca f(n) log n atunci spatiul folosit este de ordin O(f(n)) , restul demonstratiei ramanand la fel.
Problema PATH ilustreaza posibilitatea ca L NL. Pentru a aborda aceasta conjectura - nedemonstrata inca, asemenea conjecturii P NP - este necesar sa analizam problemele NL-complete. Conform Lemei 26, L P T reductibilitatea polinomiala nu este adecvata pentru compararea problemelor din NL dupa dificultatea lor. Trebuie utilizate reduceri mai "simple".
29. Definitie
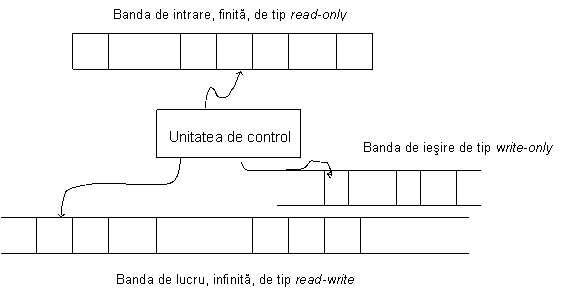
Un transducer cu spatiu logaritmic (log-space transducer) este o MT care are:
o banda de intrare, finita, de tip read-only, pe care se afla permanent secventa de intrare si numai ea;
o banda de iesire, eventual infinita, de tip write-only;
o banda de lucru infinita de tip read/write, obisnuita.
Pentru un cuvant de intrare w de lungime n transducerul utilizeaza (scaneaza) O(log n) simboluri de pe banda sa de lucru si isi incheie calculul avand pe banda de iesire cuvantul f(w) (si nimic altceva).
T numai celulele scanate de cursor pe banda de lucru determina complexitatea spatiu a acestui tip de MT.
30. Definitie
Functia f: S S* se numeste calculabila in spatiu logaritmic exista un transducer cu spatiu logaritmic care, oricare ar fi secventa w I S* de pe banda de intrare, se opreste, avand pe banda de iesire secventa f(w).
31. Definitie
Fie limbajele A, B S*. Limbajul A se numeste reductibil functional in spatiu logaritmic la limbajul B si se noteaza prin A L B ) f : S S* calculabila in spatiu logaritmic astfel incat ( ) w I S*: w I A f(w) I B.
32. Definitie
Un limbaj L se numeste NL-complet daca satisface urmatoarele doua conditii:
(1) L I NL
) A I NL: A L L .
33. Teorema
Daca A L B si B I L atunci si A I L
34. Teorema
Daca A L B si A este NL-complet atunci si B este NL-complet.
3 Teorema
Daca exista un limbaj L NL-complet cu proprietatea ca L I L , atunci L NL
36. Teorema
PATH este NL-complet.
37 Corolar
NL P .
38. Teorema
NL coNL
Ideea demonstratiei
coNL
Trebuie construit un algoritm nedeterminist cu spatiu de lucru
logaritmic pentru limbajul ![]()
Cum PATH este NL-complet (Teorema 36) rezulta ca NL coNL
39. Teorema
PolyL PSPACE
unde
![]()
este una dintre clasele de algoritmi cu spatiu de lucru logaritmic super-linear
40. Observatie
Relatiile dintre clasele de complexitate spatiu si timp - cunoscute in prezent - sunt:
L NL coNL P PSPACE
Nu stim daca vreuna dintre aceste incluziuni este stricta (desi, intr-un corolar din Capitolul 9, demonstram ca NL PSPACE Prin urmare, fie coNL P fie P PSPACE are loc dar nu stim care dintre ele! Cei mai multi dintre cercetatori presupun ca toate aceste incluziuni sunt stricte.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2787
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved