| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Ecuatii diferentiale de ordinul intai
Sa se integreze ecuatiile diferentiale:
a) ![]() ;
;
b) ![]()
Solutie
a)
Ecuatia este cu variabile separabile, deoarece este echivalenta cu
ecuatia diferentiala ![]() si deci
integrand obtinem solutia generala
si deci
integrand obtinem solutia generala ![]()
b)
Ecuatia se scrie ![]() adica
adica ![]() o ecuatie cu
variabile separabile. Solutia ei generala este
o ecuatie cu
variabile separabile. Solutia ei generala este ![]() .
.
Sa se determine solutia generala pentru ecuatiile diferentiale :
a) ![]()
b) ![]()
c) ![]()
Solutie
a) Ecuatia
se scrie sub forma ![]() , ecuatie cu variabilele separabile; deci
, ecuatie cu variabilele separabile; deci ![]() si integrand se
obtine:
si integrand se
obtine: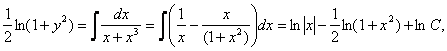 adica
adica ![]() .
.
b)
Facand substitutia ![]() obtinem
obtinem ![]() si ecuatia
va deveni
si ecuatia
va deveni ![]() , deci
, deci ![]() . Asadar
. Asadar ![]() , adica
, adica ![]() de unde se obtine
solutia data implicit
de unde se obtine
solutia data implicit ![]()
c)
Facand substitutia ![]() , adica
, adica ![]() si inlocuind in ecuatie se obtine
si inlocuind in ecuatie se obtine ![]() adica o
ecuatie cu variabile separabile
adica o
ecuatie cu variabile separabile ![]() cu solutia
cu solutia ![]() . Deci solutia generala a ecuatiei
initiale este
. Deci solutia generala a ecuatiei
initiale este ![]() .
.
Sa se integreze urmatoarele ecuatii :
a) ![]()
b) ![]()
c) ![]()
Solutie
a)
Ecuatia se scrie sub forma ![]() , adica
, adica ![]() o ecuatie cu
variabile separabile. Integrand vom obtine
o ecuatie cu
variabile separabile. Integrand vom obtine ![]()
b)
Facand substitutia ![]() se va obtine
ecuatia diferentiala liniara neomogena
se va obtine
ecuatia diferentiala liniara neomogena ![]()
In general, pentru o ecuatie diferentiala liniara
neomogena de forma ![]() , cu f si g functii continue,
solutia generala este de forma
, cu f si g functii continue,
solutia generala este de forma ![]() unde P(x) este
o primitiva a lui f(x).
unde P(x) este
o primitiva a lui f(x).
In cazul nostru, ![]() ,
, ![]() ,
, ![]() si deci
si deci ![]() , adica solutia generala a ecuatiei
initiale este
, adica solutia generala a ecuatiei
initiale este ![]() cu x>0.
cu x>0.
c)
Ecuatia fiind de forma ![]() este liniara cu
solutia generala
este liniara cu
solutia generala ![]()
Sa se determine solutia ecuatiei diferentiale:
![]()
Solutie:
Se recomanda schimbarea de functie ![]() Atunci avem
Atunci avem ![]() si ecuatia
devine
si ecuatia
devine ![]() de unde
de unde ![]() si solutia
ecuatiei este data sub forma
si solutia
ecuatiei este data sub forma 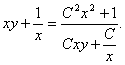
Sa se rezolve ecuatia diferentiala:
![]() .
.
Solutie
Scriem ecuatia diferentiala data in enunt sub
forma ![]() , adica
, adica 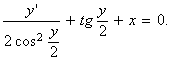 Notand
Notand ![]() vom avea
vom avea 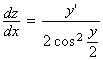 si ecuatia
devine
si ecuatia
devine ![]() adica o
ecuatie liniara neomogena cu solutia
adica o
ecuatie liniara neomogena cu solutia
![]() Asadar,
solutia ecuatiei initiale este
Asadar,
solutia ecuatiei initiale este ![]()
Sa se integreze urmatoarele ecuatii Bernoulli:
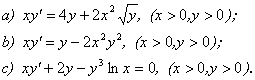
Solutie
a) La
ecuatia de tip Bernoulli ![]() se recomanda
schimbarea de functie
se recomanda
schimbarea de functie ![]() .
.
In cazul nostru ecuatia se mai scrie ![]() , deci o ecuatie Bernoulli cu
, deci o ecuatie Bernoulli cu ![]() . Impartind cu
. Impartind cu ![]() si facand
substitutia
si facand
substitutia ![]() obtinea
ecuatia liniara neomogena
obtinea
ecuatia liniara neomogena ![]() , ce are solutia generala
, ce are solutia generala ![]() . Deci solutia generala a ecuatiei
initiale este
. Deci solutia generala a ecuatiei
initiale este ![]() .
.
b)
Ecuatia are forma ![]() , deci notam
, deci notam ![]() si obtinem
ecuatia liniara neomogena
si obtinem
ecuatia liniara neomogena ![]() cu solutia
cu solutia 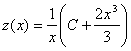 si
si ![]() .
.
c) Se imparte
ecuatia cu ![]() ; se obtine
; se obtine ![]() si notand
si notand ![]() obtinem
ecuatia liniara neomogena
obtinem
ecuatia liniara neomogena ![]() a carei
solutie este
a carei
solutie este ![]() adica
adica ![]() .
.
Sa se rezolve ecuatiile Riccati urmatoare:
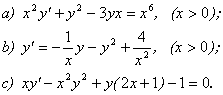
Solutie
Pentru rezolvarea ecuatiei de tip Riccati ![]() este esential de
stiut o solutie particulara a ei. Facand substitutia
este esential de
stiut o solutie particulara a ei. Facand substitutia ![]() (unde
(unde ![]() este o solutie
particulara) vom obtine o ecuatie liniara.
este o solutie
particulara) vom obtine o ecuatie liniara.
a)
Cautand o solutie particulara de forma ![]() obtinem
obtinem ![]() si facem
schimbarea de functie
si facem
schimbarea de functie ![]() . Deci
. Deci ![]() si inlocuind in
ecuatie obtinem:
si inlocuind in
ecuatie obtinem:![]() , deci
, deci
![]() , adica ecuatia liniara
, adica ecuatia liniara ![]() cu solutia
cu solutia

si solutia ecuatiei
initiale este ![]() .
.
b)
Cautam o solutie particulara de forma ![]() si gasim
si gasim ![]() . Se face schimbarea
. Se face schimbarea![]() , deci
, deci ![]() si se obtine
ecuatia liniara
si se obtine
ecuatia liniara ![]() ce admite solutia
generala:
ce admite solutia
generala:
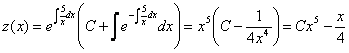 .
.
Asadar solutia generala a
ecuatiei initiale este ![]() .
.
c) Cu toate
ca este o ecuatie de tip Riccati o rezolvam prin alta
metoda. Ecuatia se scrie sub forma ![]() , adica
, adica 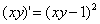 . Facem schimbarea
. Facem schimbarea ![]() si obtinem
ecuatia cu variabile separabile
si obtinem
ecuatia cu variabile separabile ![]() ce are solutia
ce are solutia ![]() , adica
, adica ![]() .
.
Sa se integreze:

Solutie
a) Notam
![]() si ecuatia
devine
si ecuatia
devine ![]() , adica
, adica ![]() o ecuatie
liniara cu solutia
o ecuatie
liniara cu solutia
![]() si solutia
ecuatiei initiale este
si solutia
ecuatiei initiale este ![]() .
.
b) Se
inverseaza rolul variabilelor, deci ![]() si ecuatia
devine liniara
si ecuatia
devine liniara ![]() , de unde
, de unde ![]() .
.
c) Folosind
acelasi rationament ca in ecuatia precedenta, deci
schimband rolul variabilelor ecuatia devine ![]() o ecuatie
liniara cu solutia
o ecuatie
liniara cu solutia ![]() .
.
Sa se integreze ecuatiile urmatoare:
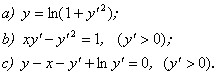
Solutie
a)
Ecuatia fiind de forma ![]() se utilizeaza
metoda parametrului: se noteaza
se utilizeaza
metoda parametrului: se noteaza ![]() si se obtine
si se obtine
![]() , din care prin diferentiere, deoarece
, din care prin diferentiere, deoarece ![]() , se deduce ecuatia
, se deduce ecuatia ![]() cu solutia
generala
cu solutia
generala ![]() . Solutia generala a ecuatiei initiale se
scrie parametric
. Solutia generala a ecuatiei initiale se
scrie parametric 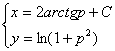 .
.
b)
Ecuatia se scrie ![]() , deci fiind de forma
, deci fiind de forma ![]() se utilizeaza tot
metoda parametrului. Notand
se utilizeaza tot
metoda parametrului. Notand ![]() obtinem
obtinem ![]() si
si 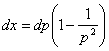 . Dar cum
. Dar cum ![]() rezulta
rezulta ![]() cu solutia
cu solutia ![]() si solutia
ecuatiei initiale este
si solutia
ecuatiei initiale este 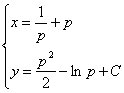 .
.
c)
Ecuatia nu poate fi scrisa sub forma normala ![]() , dar se poate explicita atat in raport cu variabila y
cand
, dar se poate explicita atat in raport cu variabila y
cand ![]() , cat si in raport cu variabila x cand
, cat si in raport cu variabila x cand ![]() .
.
In prima ipoteza notand ![]() se deduce
se deduce ![]() , iar prin diferentiere (in raport cu x) va
rezulta ecuatia diferentiala
, iar prin diferentiere (in raport cu x) va
rezulta ecuatia diferentiala
![]() , adica
, adica ![]() .
.
Daca ![]() , avem
, avem ![]() , deci
, deci ![]() , iar solutia generala este data sub
forma parametrica
, iar solutia generala este data sub
forma parametrica ![]() , cu p>0, sau sub forma
, cu p>0, sau sub forma ![]() , adica
, adica ![]() .
.
Daca ![]() , prin inlocuirea lui in ecuatia initiala
, prin inlocuirea lui in ecuatia initiala ![]() , obtinem solutia singulara
, obtinem solutia singulara ![]() .
.
Sa integram acum ecuatia, dar explicitata in raport
cu variabila x, deci scriem ecuatia sub forma ![]() , care prin derivare in raport cu y, deoarece
, care prin derivare in raport cu y, deoarece 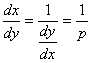 se deduce ecuatia
diferentiala
se deduce ecuatia
diferentiala 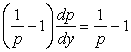 , adica
, adica ![]() . Cazul
. Cazul ![]() , deci
, deci ![]() a fost tratat mai sus;
iar
a fost tratat mai sus;
iar ![]() ne da
ne da ![]() si inlocuind in
ecuatia initiala, obtinem
si inlocuind in
ecuatia initiala, obtinem ![]() , adica s-a regasit solutia generala
anterioara.
, adica s-a regasit solutia generala
anterioara.
Sa se integreze:
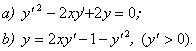
Solutie
a) Scriem
ecuatia sub forma ![]() , adica o ecuatie Clairaut. Pentru rezolvarea
acestei ecuatii derivam in raport cu x si facem
substitutia
, adica o ecuatie Clairaut. Pentru rezolvarea
acestei ecuatii derivam in raport cu x si facem
substitutia ![]() ; rezulta
; rezulta ![]() deci sau
deci sau ![]() adica
adica ![]() si inlocuind pe
si inlocuind pe ![]() in ecuatia
initiala obtinem solutia generala
in ecuatia
initiala obtinem solutia generala ![]() , sau x - p = 0, adica x = p,
, sau x - p = 0, adica x = p, ![]() si solutia
singulara este parabola
si solutia
singulara este parabola ![]() .
.
b) Este o
ecuatie Lagrange. Se noteaza ![]() deci ecuatia
devine
deci ecuatia
devine ![]() si derivand in
raport cu x rezulta
si derivand in
raport cu x rezulta ![]() . Schimbam rolul variabilelor
. Schimbam rolul variabilelor ![]() si obtinem
ecuatia liniara
si obtinem
ecuatia liniara ![]() cu solutia
generala
cu solutia
generala
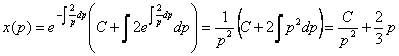 si solutia
generala a ecuatiei Lagrange initiala este data sub
forma parametrica
si solutia
generala a ecuatiei Lagrange initiala este data sub
forma parametrica
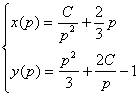 .
.
Sa se determine solutia ecuatiei diferentiale 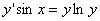 , cu conditia y
, cu conditia y![]() =1.
=1.
Solutie
Ecuatia se scrie sub forma ![]() , adica o ecuatie cu variabile separabile si
integrand obtinem
, adica o ecuatie cu variabile separabile si
integrand obtinem ![]() , deci lny=Ctg
, deci lny=Ctg![]() sau
sau ![]() Din conditia y
Din conditia y![]() =1, rezulta 1 =
=1, rezulta 1 = ![]() , adica C=0 si solutia este
, adica C=0 si solutia este ![]()
Sa se integreze ecuatiile omogene urmatoare :
a) ![]() ;
;
b) ![]()
![]()
c) ![]()
Solutie
a)
Ecuatia este de tipul ![]() anume
anume ![]() se recomanda deci
substitutia
se recomanda deci
substitutia ![]() deci
deci ![]() Ecuatia devine
Ecuatia devine ![]() deci
deci 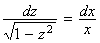 si integrand,
si integrand, ![]() , de unde
, de unde ![]() .
.
b) Scriind
ecuatia sub forma ![]() si notand
si notand ![]() obtinem
obtinem ![]() o ecuatie cu
variabile separabile. Integrand obtinem
o ecuatie cu
variabile separabile. Integrand obtinem ![]() , deci
, deci ![]() , adica
, adica ![]()
![]() si solutia ecuatiei este data sub forma
si solutia ecuatiei este data sub forma ![]()
c)
Ecuatia este omogena fiind de forma ![]() Facem substitutia
Facem substitutia
![]() si obtinem
ecuatia
si obtinem
ecuatia ![]() , adica
, adica ![]() si integrand
obtinem
si integrand
obtinem ![]() , deci
, deci ![]() si cum
si cum ![]() avem solutia
generala
avem solutia
generala ![]() .
.
. Sa se rezolve ecuatiile urmatoare :
a) ![]() ;
;
b) ![]()
Solutie
a) Se
considera dreptele ![]() ,
, ![]() din planul xOy;
ele se intersecteaza in punctul (-1,3). Facand substitutia
din planul xOy;
ele se intersecteaza in punctul (-1,3). Facand substitutia ![]() ,
, ![]() , obtinem ecuatia omogena
, obtinem ecuatia omogena ![]() , deci facem schimbarea
, deci facem schimbarea ![]() si ecuatia
devine
si ecuatia
devine
![]() , adica
, adica
![]() Integrand ecuatia
Integrand ecuatia
![]() obtinem
obtinem ![]() adica
adica ![]() si cum
si cum ![]() ,
, ![]() ,
, ![]() avem
avem 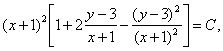 deci
deci ![]()
b) In acest
caz facem substitutia ![]() si ecuatia
devine
si ecuatia
devine ![]() , adica
, adica ![]() Separand variabilele
si integrand obtinem
Separand variabilele
si integrand obtinem ![]() deci
deci ![]()
. Sa se determine solutia
ecuatiei ![]() , ce trece prin punctul de coordonate (1,2).
, ce trece prin punctul de coordonate (1,2).
Solutie
Ecuatia fiind de forma ![]() este o ecuatie de
tip Riccati. Se vede usor ca o solutie particulara a ei este
este o ecuatie de
tip Riccati. Se vede usor ca o solutie particulara a ei este ![]() si facand
substitutia
si facand
substitutia ![]() obtinem
obtinem ![]() , adica ecuatia liniara neomogena
, adica ecuatia liniara neomogena ![]() cu solutia
generala
cu solutia
generala
![]() deci solutia generala
a ecuatiei initiale este
deci solutia generala
a ecuatiei initiale este ![]() Punand conditia
ca solutia sa treaca prin punctul de coordonate (1,2)
obtinem
Punand conditia
ca solutia sa treaca prin punctul de coordonate (1,2)
obtinem ![]() , adica
, adica ![]() si solutia
ceruta este
si solutia
ceruta este ![]()
. Sa se determine solutiile generale ale urmatoarelor ecuatii diferentiale :
a) ![]()
b)![]()
c) ![]()
Solutie
O
ecuatie diferentiala de forma ![]() cu P,Q
functii de clasa
cu P,Q
functii de clasa ![]() pe un domeniu simplu conex din
pe un domeniu simplu conex din ![]() este o ecuatie
exacta daca
este o ecuatie
exacta daca ![]() in orice punct din
D ; in acest caz in vecinatatea oricarui punct fixat
in orice punct din
D ; in acest caz in vecinatatea oricarui punct fixat ![]() exista o
functie, anume
exista o
functie, anume 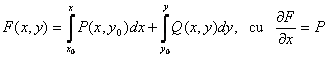 si cu
si cu ![]() , astfel incat ecuatia devine
, astfel incat ecuatia devine ![]() adica dF=0
si are solutia generala F(x, y)=C.
adica dF=0
si are solutia generala F(x, y)=C.
a) Aici ![]() si avem
relatia
si avem
relatia ![]() pe orice domeniu D din
pe orice domeniu D din ![]() , deci ecuatia este exacta. In acest caz, in
vecinatatea oricarui punct fixat
, deci ecuatia este exacta. In acest caz, in
vecinatatea oricarui punct fixat ![]() exista
functia
exista
functia 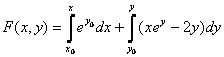 , adica
, adica
![]() si solutia
generala a ecuatiei este
si solutia
generala a ecuatiei este ![]()
Ecuatia se poate rezolva si direct:
![]() si
si
![]()
b) Daca ![]() si
si ![]() avem
avem ![]() , deci ecuatia considerata este exacta pe
, deci ecuatia considerata este exacta pe ![]() si exista in
vecinatatea oricarui punct fixat
si exista in
vecinatatea oricarui punct fixat ![]() functia
functia
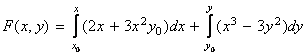 , deci
, deci
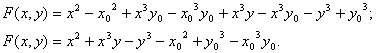
Deci, solutia generala a
ecuatiei este ![]()
![]()
Direct
avem: ![]() ,
,
![]() si
si ![]()
c) Ecuatia este exacta, cu solutia
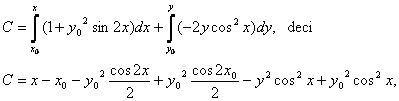
adica luand ![]() =(0,0),
=(0,0), ![]()
Direct
![]() , adica
, adica
![]() , deci rezulta
, deci rezulta ![]() si solutia
si solutia ![]()
. Folosind un factor integrant, sa se rezolve ecuatiile :
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Solutie
Daca
ecuatia diferentiala ![]() nu este exacta,
dar exista
nu este exacta,
dar exista ![]() astfel incat
ecuatia diferentiala
astfel incat
ecuatia diferentiala ![]() sa fie
exacta, atunci
sa fie
exacta, atunci ![]() se numeste factor
integrant al ecuatiei si va verifica ecuatia cu derivate
partiale
se numeste factor
integrant al ecuatiei si va verifica ecuatia cu derivate
partiale ![]()
Determinarea unui factor integrant este mai simpla in cazurile:
1) Daca raportul 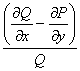 depinde numai de
variabila x, atunci se cauta
depinde numai de
variabila x, atunci se cauta![]() =
=![]() (x).
(x).
2) Daca raportul 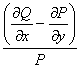 depinde numai de
variabila y, atunci se cauta
depinde numai de
variabila y, atunci se cauta ![]() =
=![]() (y).
(y).
a)
Ecuatia diferentiala nu este exacta; avem ![]() si cum raportul
si cum raportul 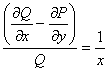 cautam un
factor integrant
cautam un
factor integrant ![]() =
=![]() (x).
(x).
Conditia ![]() ne da
ecuatia
ne da
ecuatia
![]() adica
adica ![]() ce admite solutia
ce admite solutia
![]() Asadar,
ecuatia diferentiala
Asadar,
ecuatia diferentiala ![]() este exacta (s-a
obtinut din ecuatia diferentiala initiala prin
inmultire cu
este exacta (s-a
obtinut din ecuatia diferentiala initiala prin
inmultire cu ![]() ) si are solutia generala
) si are solutia generala ![]()
b) Daca ![]() atunci
atunci ![]()
si ecuatia nu este exacta.
Raportul 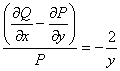 si deci
cautam un factor integrant
si deci
cautam un factor integrant ![]() =
=![]() (y). Conditia
(y). Conditia ![]() ne da
ecuatia
ne da
ecuatia ![]() ce admite solutia
ce admite solutia
![]() si ecuatia
si ecuatia ![]() este exacta cu
solutia
este exacta cu
solutia ![]()
. Folosind un factor integrant ![]() de forma
indicata, sa se rezolve ecuatiile:
de forma
indicata, sa se rezolve ecuatiile:
a)![]()
![]()
b)![]()
Solutie
a) Notand ![]() avem
avem ![]() si
si ![]() .
.
Ecuatia ![]() este exacta
daca
este exacta
daca ![]() adica
adica
![]()
Efectuand
calculele obtinem ecuatia ![]() ce are solutia
ce are solutia ![]() adica
adica ![]() Deci ecuatia
Deci ecuatia
![]() este exacta
si solutia ei verifica ecuatia
este exacta
si solutia ei verifica ecuatia 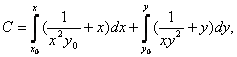 adica
adica ![]()
b) Notand ![]() obtinem
ecuatia
obtinem
ecuatia ![]() cu solutia
cu solutia ![]() , deci
, deci ![]() . Asadar, ecuatia
. Asadar, ecuatia
![]() , adica ecuatia:
, adica ecuatia:
![]()
este exacta si solutia ei verifica ecuatia
![]() , deci
, deci ![]()
. Sa se rezolve problema Cauchy:
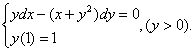
Solutie
Ecuatia nu este exacta, dar cautand un factor integrant ![]() =
=![]() (y), (deoarece raportul
(y), (deoarece raportul 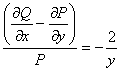 ) obtinem
) obtinem ![]() ce admite solutia
ce admite solutia
![]() . Asadar avem ecuatia exacta
. Asadar avem ecuatia exacta ![]() adica
adica ![]() rezulta
rezulta ![]() deci
deci ![]() si punand
conditia ca solutia ecuatiei sa treaca prin punctul de
coordonate (1, 1) avem C=0 si solutia problemei Cauchy este
parabola
si punand
conditia ca solutia ecuatiei sa treaca prin punctul de
coordonate (1, 1) avem C=0 si solutia problemei Cauchy este
parabola ![]()
Ecuatia
poate fi rezolvata mai simplu schimband rolul variabilelor, adica ![]() si ecuatia
devine
si ecuatia
devine ![]() adica
adica ![]() , o ecuatie liniara cu solutia
, o ecuatie liniara cu solutia ![]() si solutia
problemei Cauchy
si solutia
problemei Cauchy ![]()
. Sa se arate ca ecuatia omogena ![]() admite un factor
integrant de forma
admite un factor
integrant de forma 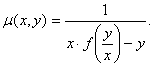
Solutie
Cum ecuatia omogena ![]() se scrie sub forma
se scrie sub forma ![]() aratam ca ecuatia
aratam ca ecuatia ![]() adica
ecuatia
adica
ecuatia 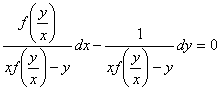 este o ecuatie
exacta.
este o ecuatie
exacta.
Deoarece
![]() adica
adica ![]() inlocuind in
ecuatie, obtinem
inlocuind in
ecuatie, obtinem 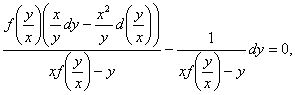
adica 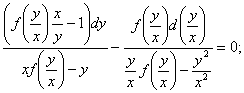 deci
deci 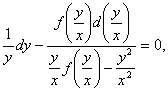 care este o
ecuatie exacta deoarece exista
care este o
ecuatie exacta deoarece exista 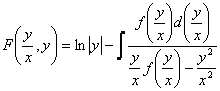 astfel incat
astfel incat ![]() si
si 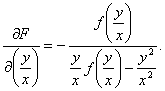
. Sa se demonstreze ca problema Cauchy
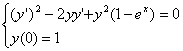
nu are solutie unica.
Solutie
Ecuatia se scrie sub forma ![]() si deci avem
ecuatiile diferentiale sub forma normala
si deci avem
ecuatiile diferentiale sub forma normala ![]() si
si ![]() care in urma unui
rationament elementar rezulta a fi echivalente cu ansamblul de
ecuatii liniare :
care in urma unui
rationament elementar rezulta a fi echivalente cu ansamblul de
ecuatii liniare :![]() ,
, ![]() , ce au solutiile generale
, ce au solutiile generale ![]() si
si ![]() Impunand conditia
initiala y(0)=1 obtinem solutiile distincte
Impunand conditia
initiala y(0)=1 obtinem solutiile distincte ![]() si
si ![]()
Exercitii suplimentare
Sa se integreze ecuatiile urmatoare :
. ![]()
R. ![]()
. ![]()
R ![]()
.![]()
R.![]()
. ![]()
R. ![]()
. ![]()
R. ![]()
.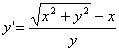
R.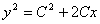
. ![]()
R. ![]()
.![]()
R.![]()
.![]()
R. ![]()
.![]()
R. ![]()
.![]()
R. ![]()
.![]()
R. ![]()
.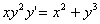
R. ![]()
.![]()
R. ![]()
.![]()
R. ![]()
.![]()
R. ![]()
.![]()
R. ![]()
.![]()
R. ![]()
. ![]()
R. ![]()
.![]()
R. ![]()
.![]()
R. ![]()
. ![]()
R. ![]()
.![]()
R. ![]()
. ![]()
R. ![]()
.![]()
R. ![]()
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 1606
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved