| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Elemente de statistica matematica
Metodele statistice joaca un rol important si in continua crestere in diferite domenii de activitate, cum ar fi: ingineria, agricultura, administratia de stat, asigurarile, economia, chimia, fizica, astronomia, biologia, medicina, sociologia, psihologia etc. In toate domeniile enumerate apar problemele in care este imposibil sa se faca masuratori sau observatii precise, sau in care evenimentele nu se repeta exact in acelasi mod. Analiza unor astfel de probleme implica o incertitudine considerabila. Metodele statistice prin ele insesi se preteaza la analiza unor astfel de probleme, furnizand mijloacele, ce indica, cu un anumit grad de siguranta, dezvoltarea ulterioara.
Statistica fiind stiinta ce are drept scop culegerea, analiza si interpretarea probabilistica a datelor, raspunde la probleme de felul urmator:
Cum sa se organizeze un plan pentru obtinerea unor astfel de date incat concluziile obtinute sa fie adevarate?
Cum sa se analizeze datele obtinute?
Concluziile obtinute pot fi extinse cu incredere?
Metodele statistice au facut ca metodele clasice de cercetare din diferite domenii sa fie mai incisive, totodata facand posibila planificarea acestor experiente in care intervin un numar mare de factori si obtinerea de noi succese.
Odata cu intensificarea folosirii metodelor stiintifice, asistam la o crestere considerabila a volumului masuratorilor de diferite feluri. Deoarece multe din aceste cercetari sunt facute fara o cunoastere temeinica si intelegere a domeniului respectiv si masuratorile facute si folosite sunt selectii, tehnicile statistice, planificarile de experiente devin mai importante ca oricand.
Tehnicile folosite in statistica tind sa rezume diferentele dintre indivizii populatiei la folosirea unor parametri cum ar fi: media, modul, mediana, abaterea medie patratica etc. Pentru anumite persoane , necercetarea fiecarui individ al populatiei constituie o pierdere, cu toate ca sintetizarea unei cantitati mari de informatie este unul dintre rezultatele cele mai folosite ale statisticii.
Obiectul statisticii
Statistica se ocupa cu gruparea, analiza si interpretarea datelor referitoare la anumite fenomene, precum si unele previziuni privind producerea lor viitoare.
Statistica este descriptiva sau formala, cand se ocupa cu culegerea si inregistrarea datelor si matematica, cand analizeaza, interpreteaza sau efectueaza previziuni.
Limbajul statisticii
Definitie:
Se numeste populatie statistica orice multime care formeaza obiectul unei analize
statistice.
Elementele unei populatii statistice se numesc unitati statistice sau indivizi.
Definitie:
Trasatura (proprietatea) comuna a tuturor unitatilor unei popularitatii statistice se numeste caracteristica.
Exemple:
a) In cazul repartitiei elevilor din clasa a X-a dupa notele obtinute la matematica:
multimea tuturor elevilor din clasa formeaza populatia statistica;
fiecare elev este o unitate statistica;
nota obtinuta la matematica este caracteristica studiata;
b) In cazul repartitiei profesorilor de matematica din tara dupa varsta:
multimea tuturor profesorilor de matematica constituie populatia statistica;
fiecare profesor de matematica este o unitate statistica;
varsta fiecarui profesor este caracteristica populatiei;
c) Multimea elevilor Liceului ENERGETIC din orasul Rm. Valcea constituie o populatie statistica, fiecare elev este o unitate statistica iar sexul, talia, anul nasterii, grupa sanguina, prima limba straina studiata pot fi caracteristici ale populatiei.
3.1 Natura statistica a stiintei
Stiinta este statistica chiar in punctele sale culminante. Aceasta inseamna ca "legile stiintifice" nu exprima cu certitudine felul cum se comporta natura, legile stiintifice descriu pur si simplu modul cum s-a comportat natura intre anumite limite, si modul cum probabil se va comporta din nou intre anumite limite, in conditii similare. Este de competenta statisticii de a determina care sunt aceste limite, intr-un concurs special de conditii delimitative, si de a elabora probabilitatea de repartitie a oricarui concurs de evenimente date, in lumina frecventei si regularitatii cu care au aparut in trecut.
Nu putem spune cu certitudine ca soarele va rasari maine. Dar putem spune in mod cu totul justificat ca, fara vreo exceptie care sa fi fost inregistrata vreodata, soarele a rasarit in fiecare zi de la inceputul istoriei, si ca nu s-a schimbat in mod apreciabil niciuna din conditiile cunoscute ale rasaritului sau; de aceea este foarte probabil ca va rasari maine. De asemenea, judecand dupa cele petrecute in trecut, este probabil ca, in regiunile de latitudine nordica, ziua de 1 ianuarie sa fie in viitor mai rece decat cea de 1 aprilie. Totusi nu putem fi siguri de aceasta; caci ziua de Anul Nou este, cateodata, mai putin friguroasa, iar pe de alta parte s-a constatat ca la 1 aprilie, uneori a nins. Deoarece in aceste chestiuni exista variatii considerabile, nu este de loc dincolo de limitele posibilitatii ca un 1 ianuarie extraordinar de nefriguros si de un 1 aprilie extraordinar de racoros sa survina in viitor, in acelasi an. Daca acest fenomen s-ar intampla, relatiile normale de temperatura s-ar gasi in situatia de a fi inversate. Oricat de mica ar fi probabilitatea ca soarelui sa i se nazareasca intr-o buna dimineata sa nu mai rasara, afirmam aceasta cu oarecare incredere, pentru ca contrastul dintre constanta miscarilor soarelui in trecut si inconstanta conditiilor de temperatura este izbitoare. In acest fel, ne dam seama ca gradul de probabilitate a reaparitiei in viitor a unui eveniment este in directa legatura cu gradul de constanta sau lipsa de variabilitate in aparitiile sale din trecut. Statistica se ocupa, intr-o mare masura, cu valorile medii ale evenimentelor survenite in trecut, cu variabilitatea in jurul acestor valori medii si cu probabilitatea evenimentelor viitoare in conformitate cu aceste valori medii din trecut.
Din punct de vedere statistic, diferenta esentiala dintre psihologie si stiinte cum sunt fizica si chimia, consta in variabi1itati1e fenomenelor. Fenomenele psihologice au o variabilitate cu mult mai mare decat fenomenele fizice, si prin urmare ele sunt mai putin previzibile. Acest lucru este conditionat de numarul covarsitor mai mare de variabile care intra in determinarea unui comportament uman sau animal. Pentru a ilustra aceasta vom face uz de o comparatie dintre o experienta familiara din domeniul fizicii si un experiment relativ simplu din psihologie.
La verificarea uzuala a legii lui Boule Mariotte in laboratorul de fizica ne intereseaza relatia dintre volumul si presiunea unui gaz inclus intr-un recipient. Dorim sa stim cum variaza volumul gazului ca o consecinta a variatiei sistematice a presiunii. In afara volumului si presiunii exista o singura variabila importanta de care trebuie sa ne ocupam: temperatura. Este clar ca daca nu pastram temperatura constanta, variatiile de volum rezultante vor fi consecinte atat a variatiilor de temperatura cat si a celor de presiune, Si nu vom sti ce cota parte va trebui sa atribuim fiecareia dintre aceste variabile. Dar este o chestiune relativ simpla de a pastra cea de-a treia variabila constanta in decursul intregii experiente. Variatiile de volum pot fi, in mod definitiv, legate de variatiile de presiune, si se poate formula o lege care sa le guverneze in limitele erorilor de experimentare.
In contrast cu aceasta problema, din domeniul anorganic, caracterizata prin prezenta a trei variabile clar definite, sa luam acum o problema din domeniul psihologiei experimentale.
Sa presupunem ca vrem sa cercetam efectul alcoolului asupra performantelor mentale. Pentru a specifica, sa consideram determinarea efectului produs de 3 uncii de bautura alcoolica asupra performantelor la un test de adunare aritmetica, la 15 minute dupa absorbtia bauturii respective. Dam o descriere sumara a procedurii: mai intai, se da subiectilor un test initial; apoi, se introduce factorul experimental (in acest caz: alcoolul); dupa scurgerea intervalului de timp specificat se procedeaza la testul final. Acum, daca alcoolul are vreun efect ar trebui sa ne asteptam, in general, la o diferenta intre rezultatele obtinute la testul initial si cele obtinute la testul final. Dar putem noi oare sa atribuim orice diferenta, care ar putea surveni, numai si numai factorului experimental ? Din nefericire: nu ! Caci, fara a epuiza posibilitatile, putem insira un mare numar de alte variabile pe seama carora se poate pune cel putin o parte a cauzelor variatiei: oboseala, exercitiu si practica in operatia de adunare, dificultati inegale in executarea color doua teste, grade diferite de distragere datorate zgomotului sau variatiei de iluminare, durata diferita in asa-zisa ,,incalzire". In concentrarea atentiei, in revenirea din stari de plictiseala, sugestia bazata pe notiuni preconcepute asupra efectului alcoolului s.a.m.d. Fata de aceasta formidabila insiruire de influente exterioare, s-ar parea ca intentia de a izola efectul factorului experimental in chestiune, si anume alcoolul, este cu totul lipsita de speranta. Si totusi nu este un caz deznadajduit: caci se poate obtine o izolare a multora dintre aceste variabi1e perturbatorii cu ajutorul unui "grup do control"
Serie statistica
Definitie:
Fie o populatie statistica cu caracteristica X care ia valorile x1,
x2, .,xp si ni, ![]() ,
numarul de indivizi pentru caracteristica X ia valoarea xi.
,
numarul de indivizi pentru caracteristica X ia valoarea xi.
Multimea perechilor (xi, ni), ![]() ,
este o serie statistica. Numerele ni le vom numi efective, frecvente
absolute sau frecvente.
,
este o serie statistica. Numerele ni le vom numi efective, frecvente
absolute sau frecvente.
O serie statistica este, de obicei, prezentata sub forma unui tablou de tipul urmator:
|
Valoarea caracteristicii |
x1 x2 . xi . xp |
|
Frecvente |
n1 n2 ni . np |
sau:
|
Intevale (clase) |
xo-x1 x1-x2 . xp-1 -xp |
|
Frecvente |
n1 n2 . np |
Un interval (clasa) (xi, xi+1) se citeste de la xi la xi+1) sau intre xi si xi+1.
Exemplul 1:
Repartitia elevilor unei clase dupa notele de la proba de evaluare la matematica genereaza seria urmatoare:
|
Nota | |
|
Frecventa |
Exemplul 2:
Seria statistica ce ilustreaza repartitia elevilor dintr-o clasa dupa inaltime (talie)este urmatoarea:
|
Talia (in m) |
|
|||||
|
Frecventa |
Exemplul 3:
Aruncand simultan doua zaruri (pana se obtin in total 1000 de puncte) si retinand suma cifrelor obtinute, se poate obtine urmatorul tablou al unei serii statistice:
|
xi |
2 3 4 5 6 7 8 9 |
|
ni |
23 54 86 114 131 177 142 109 |
|
xi | |
|
ni |
Unde xi,![]() , reprezinta sumele posibile de puncte obtinute la aruncarea a doua zaruri iar
ni numarul de aparitii al sumei xi.
, reprezinta sumele posibile de puncte obtinute la aruncarea a doua zaruri iar
ni numarul de aparitii al sumei xi.
Exemplul 4:
Populatia municipiilor si oraselor judetului Constanta la recensamantul din 7 ianuarie 1992:
|
Orasul | |||||
|
Nr. loc. |
|
Orasul | ||||||
|
Nr. loc. |
Unde: 1 - Constanta, 2 - Basarabi, 3 - Cernavoda, 4 - Eforie, 5 - Harsova, 6 - Mangalia, 7 - Megidia, 8 - Navodari, 9 - Negru Voda, 10 - Ovidiu, 11 - Techerghiol.
Definitie:
Fie (xi, ni) o serie statistica. Numarul ![]() se numeste frecventa absoluta cumulata crescatoare
a valorii xi.
se numeste frecventa absoluta cumulata crescatoare
a valorii xi.
Exemplu:
In cazul seriei din exemplul 1, avem:
N1=1=n1,N3=9,N5=20 si N10=30.
Definitie:
Fie (xi, ni) o serie statistica cu p valori. Numarul ![]() se numeste frecventa absoluta cumulata descrescatoare
a valorii xi.
se numeste frecventa absoluta cumulata descrescatoare
a valorii xi.
Exemplu:
In cazul seriei din exemplul avem:
N1'=30=N, N3'=26,N'8=2=n8
Definitie:
Fie seria statistica (xi, ni) cu efectivul total N.
Numarul real ![]() se
numeste frecventa relativa a valorii xi.
se
numeste frecventa relativa a valorii xi.
Observatii:
Din definitie rezulta ca ![]() .
.
Frecventa relativa se scrie deseori in procente.
Frecventele definite mai sus se trec de obicei in tabelul seriei statistice astfel (exemplul 2):
|
Nota |
Frecventa absoluta |
Frecventa relativa |
Frecventa absoluta cumulata descrescatoare |
Frecventa absoluta cumulata crescatoare |
Frecventa relativa cumulata descrescatoare |
Frecventa relativa cumulata crescatoare |
|
|
Din acest tablou se obtin informatii diverse. Astfel:
a) numarul 15, aflat la intersectia liniei a 4-a cu coloana a 5-a din tablou, arata ca sunt 15 elevi care au obtinut note sub 6.
b) numarul 0.13, aflat la intersectia liniei a 2-a cu coloana a 7-a a tabloului, arata ca 13% din elevi au obtinut sub 5.
c) numarul 0.2, aflat la intersectia liniei a 4-a cu coloana a 3-a a tabloului, arata ca 20%din elevi au obtinut nota 6.
4.Serii cronologice
Definitie:
O serie (xi, ni), unde xi reprezinta un timp sau un interval de timp iar ni valoarea corespunzatoare unei marimi (care evolueaza in timp), se numeste serie cronologica.
Exemple:
a) temperatura aerului la 1 noiembrie a fiecarui an in Bucuresti genereaza seria cronologica urmatoare (datele sunt trecute cu aproximatii):
|
Data |
Temperatura (ºC) |
b) populatia scolara din invatamantul de toate gradele:
|
An scolar |
Nr. total elevi si studenti |
5.Reprezentarea grafica a seriilor statistice
Asa cum aratam la prezentarea obiectului statisticii matematice, dupa culegerea si inregistrarea datelor urmeaza analiza si interpretarea acestora.
Un prim pas de interpretare intuitiva a datelor il constituie reprezentarea grafica a serilor statistice.
Graficul unei serii statistice se numeste diagrama.
In cele ce urmeaza vom prezenta cateva modalitati de intocmire a diagramelor unor serii statistice cu o singura caracteristica.
5.1. Diagrame in batoane
Constructia diagramei in batoane se face astfel:
pe axa absciselor unui sistem de axe ortogonal xOy se considera valorile caracteristicii:xi;
pe axa ordonatelor se considera efectivele ( frecventele absolute ):ni
segmentul cu capetele punctele de coordonate: (xi,0) si (xi,ni), reprezinta batonul corespunzator valorii xi.
Exemplu:
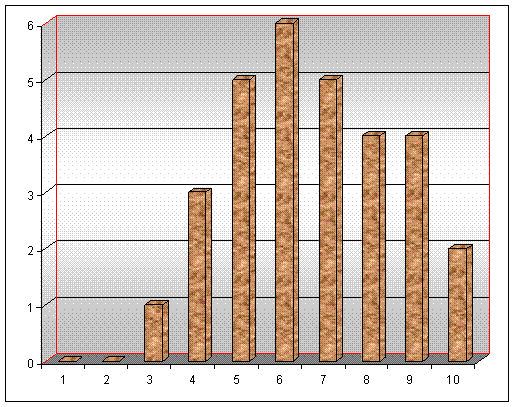
In cazul seriei cu notele elevilor unei clase, la matematica:
|
Nota |
4 5 6 7 8 9 10 |
|
Frecventa |
se obtine urmatoarea diagrama in batoane:
Observatii:
Unitatile de masura nu se iau, de regula, aceleasi pe axa Ox si pe axa Oy
Diagrama in batoane, se deduce, poate fi utilizata pentru valori mici ale efectivelor
Diagrama in batoane este sugestiva; rezultatele se interpreteaza usor vizual dupa inaltimea batoanelor.
5.2. Diagrame prin coloane
Coloanele sunt dreptunghiuri cu bazele egale si inaltimile proportionale cu efectivele (frecventele absolute) ale unei serii statistice.
Exemplu:
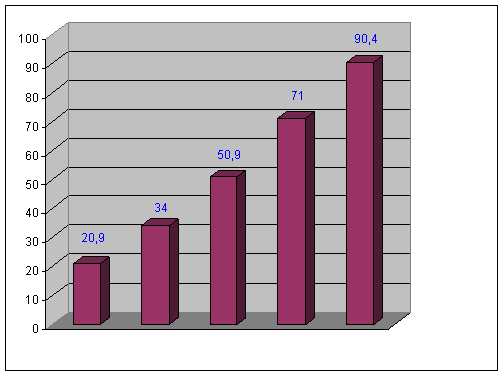
Fie seria generata de cheltuielile social-culturale de la bugetul statului in anii 1965-1985
|
xi: Anii | |||||
|
ni: miliarde lei |
Observatii:
Diagrama prin coloane poate fi graficul unei serii cu valori mari ale efectivelor, spre deosebire de diagrama prin batoane. Din acest motiv aceasta diagrama este mai adesea utilizata in statistica.
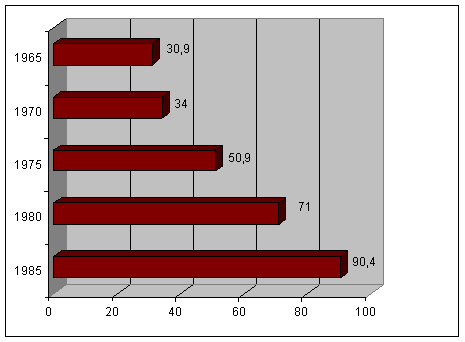
Dreptunghiurile din diagrama prin coloane pot fi asezate orizontal si atunci reprezentarea grafica se numeste diagrama prin benzi.
Prezentam in continuare diagrama prin coloane si prin benzi pentru exemplul anterior.
1970 1975 1980 1985
5.3. Poligonul frecventelor
Poligonul frecventelor se construieste astfel:
pe axa Ox se reprezinta intervalele de timp (xi,xi+1) 1≤i≤p
pe axa Oy se reprezinta frecventele absolute ni, 1≤i≤q
se unesc succesiv punctele de coordonate (mi, ni), unde mi sunt coordonatele mijloacelor segmentelor (xi,xi+1).
Exemplu:
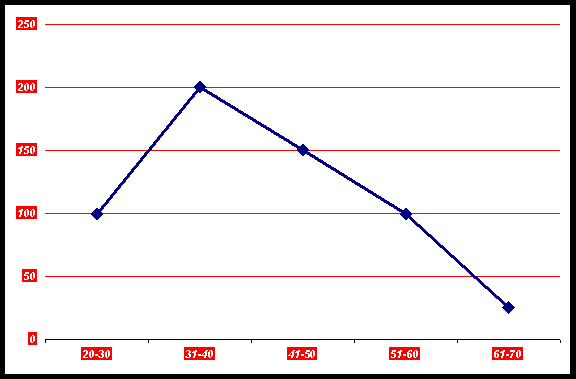
In cazul seriei reprezentand gruparea salariatilor unei societatii pe varste se obtine urmatorul poligon:
|
Grupe de varsta |
20-30 ani |
31-40 ani |
41-50 ani |
51-60 ani |
61-70 ani |
|
Nr. salariatilor |
Observatii:
Poligonul frecventelor cumulate (crescatoare) se obtine unind succesiv, printr-o linie poligonala, punctele de coordonate (xi+1, ni+1) unde xi+1 este extremitatea dreapta a intervalului (xi, xi+1), iar ni+1 frecventa cumulata a clasei (xi, xi+1) sau corespunzatoare valorii xi+1.
Exemplu:
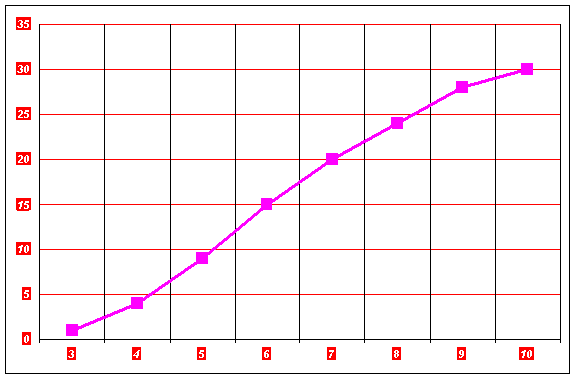
In cazul seriei reprezentand notele obtinute la proba de evaluare la matematica:
|
Nota | |
|
Frecventa absoluta | |
|
Frecventa cumulata crescatoare |
Se obtine poligonul frecventelor cumulate crescator, urmatorul:
5.4. Cronograme
Seriile cronologice se reprezinta grafic, de regula prin poligrame de frecventa sau cronograme astfel:
pe axa Ox de reprezinta momentele xi sau intervalele de timp (xi,xi+1).
pe axa Oy se reprezinta efectivele ni.
unind succesiv punctele de coordonate (xi, xi+1) se obtine cronograma sau histograma respectiva.
Exemplu:
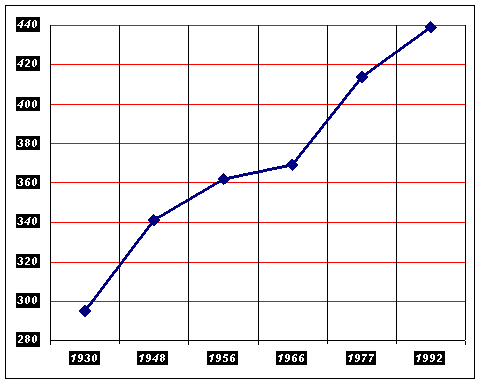
Evolutia in timp a populatiei judetului Valcea genereaza seria statistica:
|
Anii | |
|
Locuitori (mii) |
cu cronograma urmatoare:
5.5. Alte modalitati de reprezentare grafica a seriilor statistice
a) Diagrame circulare
In diagrama circulara aria cercului va reprezenta suma totala, N, a valorilor ni, 1≤i≤p, iar fiecare ni va fi reprezentata printr-un sector de cerc cu aria proportionala cu valoarea ni.
Exemplu:
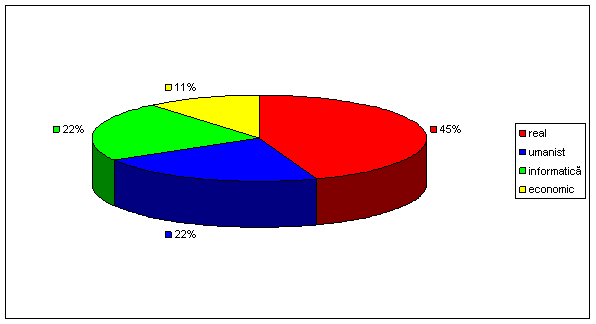
Repartizarea elevilor de la Liceul Teoretic Al. Odobescu din Lehliu Gara pe profile, in anul scolar 1994/1995, genereaza seria statistica urmatoare:
|
Profilul |
real umanist informatica economic |
|
Numar elevi |
Asadar, la 360º ii corespund 540 elevi.
Aplicand regula de trei simpla se obtine:
240.........x
![]()
Analog, la 120 de elevi corespund 80º, iar la 60 de elevi corespund 40º.
Rezulta urmatoarea diagrama circulara:
b) Diagrame prin patrate. Diagrame prin cercuri.
Prin aceste diagrame patratele sau cercurile de laturi, respectiv raze diferite reprezinta proportional, valorile ni ale caracteristicii (unidimensionale).
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 7072
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved