| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
DOCUMENTE SIMILARE |
||||
|
||||
1. Definitie .Fie f o functie f: |R [0,1) ,astfel incat
(x) = x-[x] = ,
unde [x] se numeste partea intreaga a numarului x cu proprietatea
[x] x < [x] + 1, ( ) x I|R.
Partea intreaga se noteaza cu .
Exemple: = 0,35 ; = 0,22.
Dupa cum ati putut constata, "conjugata" functiei "parte fractionara" este functia "parte intreaga" care se poate defini astfel:
Fie g: |R T Z astfel incat g(x)= [x].
Astfel, cele doua functii au proprietatea : g(x) + f(x) = x.
2.Graficul functiei
1)Tabel de valori
![]()
X [-1 - - - 0) [0 1) [1 1 1 1 2) [2 2 2 2 3]
![]()
f(X) [ 0 1) [0 1) [0 1] [0 1]
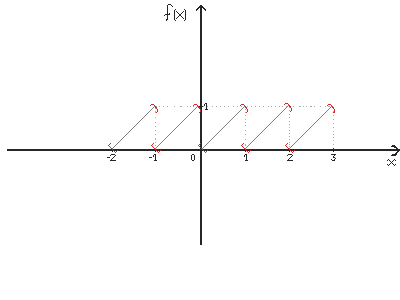
2)Desen grafic

Observatie. Graficul functiei 'parte fractionara' contine o infinitate de segmente oblice ce alcatuiesc cu axa absciselor un unghi de 45 de grade, segmente cu o extremitate deschisa si una inchisa ,motiv pentru care aceasta functie se mai numeste functia 'parcare oblica '.
3.Proprietati ale functiei
1). Functia 'parte fractionara' este o functia periodica avand ca perioada principala T=1.
Fie k I Z,
rezulta ca f( x + k*T) = ( x + k*T) - [ x + k*T]= x - [x] = f(x) .
2). Functia 'parte fractionara' este o functie surjectiva, deoarece oricare ar fi y I |R , exista prin definitie cel putin un numar x ce apartine intervalului [0,1) cu proprietatea ca f(x)= y.
3).Functia 'parte fractionara' are urmatoarea proprietate :
oricare ar fi k I Z, aceasta functie este strict crescatoare pe intervalul [k, k+1).
Demonstatie: Vom lua ca interval de referinta intervalul [0, 1)
Fie doua numere x si y ce apartin acestui interval. Presupunem ca x > y , rezulta ca
x) - f(y) = ( x - [x] ) - ( y - [y] );
Dar [x] = [y] = 0, rezulta ca f(x) - f(y) = x - 0 - y + 0 = x - y > 0, rezulta ca functia este strict crescatoare pe intervalul [0, 1).
4. Relatii ale functiei "parte fractionara"
Partea fractionara a modulului unui numar real
Oricare ar fi x I |R, avem relatia
![]() ,
daca xI
,
daca xI
1 - , daca x I
Oricare ar fi x I |R si f, g sunt doua functii f: |R T si g:|RT astfel incat
![]() daca xI
daca xI
f(x) =
daca x I
![]() - daca xI
- daca xI
g(x) =
daca x I 0) , atunci
= f(x) - g(x)
Relatie intre "partea fractionara" si "partea intreaga" a numerelor reale
+ < 1 [x + y] = [x] + [y] , oricare ar fi x si y I |U , unde
|U = < 0 }
5.Ecuatii si inecuatii cu functia 'parte fractionara'
Tipuri de ecuatii
1).=1/k ,unde x I |R ,iar kI (1,+OO)
Solutia acestei ecuatii este multimea S cu proprietatile :
S=
2). = k, a, b, k I |R, a
a). Daca k I [0,1) , atunci
ax + b = k + m, mIZ T x = ( k + m - b ) / a T S = .
b). Daca k 1), atunci S =
3). [ax + b , a, b I |R, a
![]() [ax
+ b] I Z T [ ax + b ]=0 si x I Z
[ax
+ b] I Z T [ ax + b ]=0 si x I Z
I ) x I |R
[ ax + b ] = 0 ax + b < 1 -b ax < 1 - b -b / a x < (1-b) /a
T S =.
Tip de exercitiu cu functia "parte fractionara":
Determinati domeniul de definitie D al urmatoarei functii :
f :D |R, f(x)=ax+b , m, n, a, b I |R
![]() m{x)+n
m{x)+n
Conditie de existenta : -n/m.
1). Daca -n/m ), atunci D= |R.
2). Daca -n/m I ), atunci
D=|R - =-n/m}.
TESTUL 1
1.Determinati multimile: A = { x I |R | = 0},
B={ x I |R | = x + 1},
C= = (x - 5) / 2}.
Rezolvare:
a). = 0 x I |R T A = Z;
b). = x+1 x- = 1 [x] = -1 x < 0 x I T B=[-1,0);
c). = (x +1) /3-2 ( x + 1)/3- = 2 [(x+1)/3] = 2
![]() 2 (x+1)/3<3 x+1<9 x<8 xI TC=.
2 (x+1)/3<3 x+1<9 x<8 xI TC=.
xIZ
2.Rezolvati urmatoarele ecuatii:
a). [( 2x +1) / 3] =
b)
![]()
![]()
![]() c). xx+5x+6 2
c). xx+5x+6 2
![]() 2+cos x
2+cos x
![]() Rezolvare:
Rezolvare:
a). [(2x+1)/3[T1] IZ T[( 2x + 1) /3] = = 0 [( 2x + 1)/3] = 0 si xIZ
I
![]() 0 (2x+1)/3<1 (2x+1)<3 xI TS=;
0 (2x+1)/3<1 (2x+1)<3 xI TS=;
xIZ
b). = 1/3 (3x-1)/2 = a+1/3, aIZ x = 2/3a +5/9 T
S
![]()
![]()
![]()
![]() c) . x +5x+6 1
c) . x +5x+6 1
2+cos x T S=
2/ 3 <1
3.Determinati domeniul maxim de definitie al urmatoarei functii :
f :D |R, f(x) = x /.
Rezolvare: Conditie de existenta x Z T D= |R- Z.
4.Ordonati crescator numerele: ,,.
Rezolvare: =
= 3 - 1 si
![]()
![]() =
=
Dar ( T 5-2< T 5-2< 2-1< T
( 2+1) si 2-1<
5+2>
T<<.
Punctaj: oficiu 1p
ex.1.3p
ex.2.3p
ex.3.1p
ex.4.2p
TESTUL 2
1.Determinati multimile:
A={x I |R | = 1/2 },
![]()
![]()
![]() B==x log 2 +
2 + 1/3sin(p
B==x log 2 +
2 + 1/3sin(p
C==
Rezolvare:
a). A=;
b). x log 2 + 2 + 1/3sin(p/6) = (1/2)x + 2 + (1/3)(1/2) = x/2 + 17/6 = (3x + 17) / 6T
T = ( 3x + 17 ) / 6 ( 3x + 5 ) / 6 - [( 3x + 5 ) /6] =(3x+17)/6
[( 3x + 5 ) / 6] = -2 (3x + 5) / 6 < -1 3x + 5 < -6
-17 3x<-11 x I 17 / 3 , -11 / 3 ) T B = [ -17 / 3 , -11 / 3) ;
![]()
![]()
![]()
![]()
![]()
![]()
c).9+4 T
![]()
![]()
![]()
![]()
![]() 3+2 T
3+2 T
=5 + 3 T 2,dar
![]() I ) TC=
I ) TC=
5 + 3 2 > 1
2.Rezolvati ecuatiile:
![]() a).
[( 3x + 5 ) / 6]=,
a).
[( 3x + 5 ) / 6]=,
b)
c). = p
Rezolvare:
![]() a).[( 3x + 5)
/ 6]IZ T [( 3x + 5 ) / 6] = 0 si xIZ T
a).[( 3x + 5)
/ 6]IZ T [( 3x + 5 ) / 6] = 0 si xIZ T
I
![]() T (3x
+ 5) / 6< 1 3x
+ 5 < 6 3x
< 1 xI T
T (3x
+ 5) / 6< 1 3x
+ 5 < 6 3x
< 1 xI T
xIZ
xI TS=;
![]() b).Conditie de existenta: xI
b).Conditie de existenta: xI
I ) TS =
![]() 5 23
>1
5 23
>1
c). = p (4x - 5) / 12 = p/6 + a, aIZ
4x - 5 = 2p + 12a x = p/2 + 5/4 + 3a T
TS=.
3.Determinati domeniul maxim de definitie al urmatoarei functii:
:D [0 , +∞ ), f(x) = (log x - 5) / .
![]()
![]()
![]() Rezolvare: mon
Rezolvare: mon
Conditii de existenta: x Z x Z T
log3 x - 5 log x 5 xI
TD = (243 , +∞) Z.
Punctaj:
oficiu..1p,
ex.1... 3p,
ex.2....3p,
ex.3....3p .
TESTUL 3
Sa se reprezinte grafic urmatoarele functii:
( x ) = 2 - 1.
g : |R [0,1), f(x)=.
Rezolvare: Se realizeaza tabelele de valori si se traseaza graficele in coordonate(x,f(x)).
Sa se calculeze x I |R, stiind ca:
![]() a). C = [x]
a). C = [x]
= log 3 + sin(p
![]() b). [x] = lg100
(1 + i)(3 - i) / (2 + i) ]
b). [x] = lg100
(1 + i)(3 - i) / (2 + i) ]
= 0,15 + 2lg6
![]()
c). [x] = 1 + 2 + .. + 1999
![]() Rezolvare:
Rezolvare:
a). C = [x] [x] = 4!/2! [x]=6; Tx = +[x] =27/4
= log 3 + sin(p
b). [x] = 2 - (1- i 1 + i) [x] = 2 - 2 = 0 T x = T
T x = 0,15 + lg36>1 T x I
c) x] = 2000 T [x] = 1 999 000;
Demonstram prin inductie matematica faptul ca:
(1/2!) + . + [(n - 1) / n = 1 - (1/n!) T
T T
Tx = [x] + = 1999 000 + 119/120.
Sa se rezolve urmatoarele inecuatii:
a [ x ];
b). + 7 > x;
c). 3[x] + 6 < 0;
d). > 1/3.
![]() Rezolvare: a). I T I T [x] < 6 x I T S =
(-
Rezolvare: a). I T I T [x] < 6 x I T S =
(-
+ 5 [x]
b). + 7 I 8) T x I T S = (-
c) [x] + 6 = 3x + 3 < 0 x < x I S = (-
d). S = .
4. Sa se ordoneze crescator numerele urmatoare:
, [log 4 + cosp p
Rezolvare: vezi testul anterior.
Punctaj: oficiu .1p
ex.1. 2p
ex.2. 3p
ex.3. 3p
ex.4..1p.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 10456
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved