| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
Metode numerice - metoda coardei
Dem: (metoda Coardei)
![]()
a) ![]() b)
b) ![]()
a) Secventa e aplica in varful
![]() care este varf mobil.
care este varf mobil.
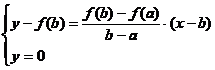
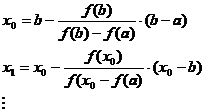
![]()
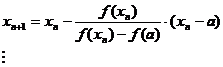 sir descrescator de numere reala ale aproximatiei
sir descrescator de numere reala ale aproximatiei
b) Secanta se aplica in varful
![]() care este
varf mobil, B-varf fix.
care este
varf mobil, B-varf fix.
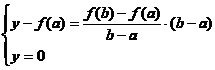
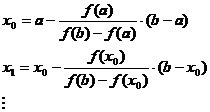
![]()
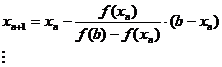 sir crescator de iteratii
sir crescator de iteratii
![]()
![]() sir convergent
sir convergent
![]()
![]() (radacina este
separate in interiorul
(radacina este
separate in interiorul ![]()
Evaluarea restului la metoda coardei
Pentru
evaluarea erorii consideram ca ![]() si
si ![]() au semene
constante pe
au semene
constante pe ![]() si
si ![]() unde
:
unde
: ![]() .
.
Consideram
cazul ![]()
![]()
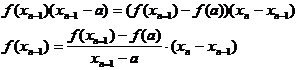
Dar ![]() este
radacina lui
este
radacina lui ![]()
![]() si
si ![]() astfel
incat:
astfel
incat:
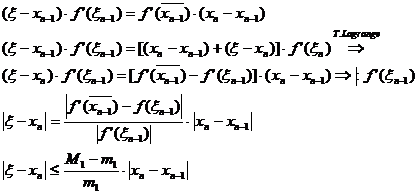
Pentru ![]() sufficient de mic avem
sufficient de mic avem
![]()
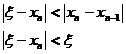
Aplicatie:
Determinati
radacina pozitiva a ecuatiei: ![]() cu eroarea
0,002.
cu eroarea
0,002.
Calculam intervalul:
![]()
![]()
![]()
![]()
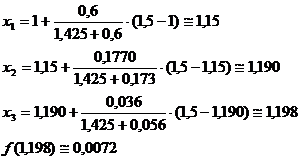
![]()
![]()
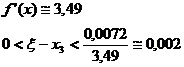
![]()
![]()
Metoda combinata
I.
![]()
![]() Th. Clestelui
Th. Clestelui
II.
![]()
![]()
III.
![]()
IV.
![]()
In cazul II :
Coarda
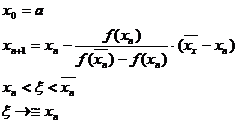
Tangenta
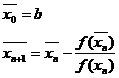
Metoda aproximatiilor succesive
![]() are in intervalul [a,b] o singura radacina
are in intervalul [a,b] o singura radacina
![]()
![]() Daca
Daca ![]() este o radacina a
ecuatiei (1) atunci ea este si radacina pentru ecuatia (2).
este o radacina a
ecuatiei (1) atunci ea este si radacina pentru ecuatia (2).
Fie ![]() Є [a,b]
Є [a,b] ![]()
![]()
![]()
![]()
![]()
. (3) sirul aproximatiilor succesive
![]()
![]()
TEOREMA:
1.
![]() derivabila
derivabila
2.
![]() derivata marginita
derivata marginita ![]()
![]()
1.
Sirul iteratiilor (3) este convergent
catre ![]()
2.
![]() este unic
este unic
DEMONSTRATIE:
1.
Fie ![]() astfel incat
astfel incat
![]()
![]()
![]()
![]()
![]() 1.
1.
2. ![]()
![]() astfel incat
astfel incat
![]()
Evaluarea erorii:
Sa dezvoltam pe ![]() in jurul lui
in jurul lui ![]()
![]()
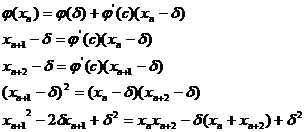
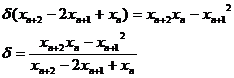 (Aitken metoda celor trei abscise)
(Aitken metoda celor trei abscise)
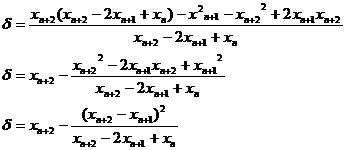
OBSERVATIE: Aceasta relatie permite ca pe baza a trei valori succesive sa se determine o valoare noua imbunatatita.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 647
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved