| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
PRIMITIVE
I. 1. Sa se stabileasca daca o functie admite sau nu primitive
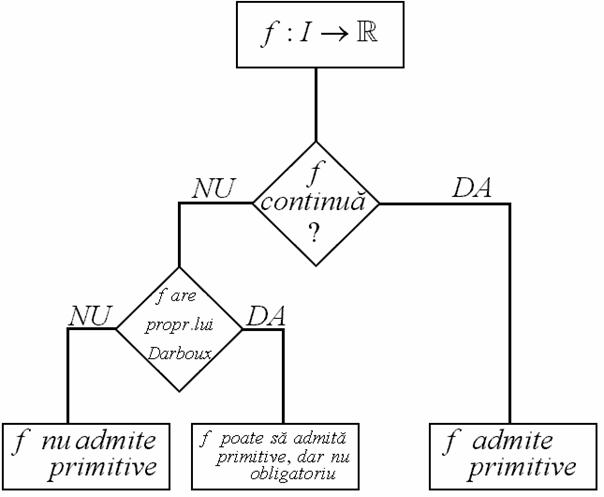
I. 2. Proprietati ale functiilor care admit primitive:
a)
Functia
care admite primitive are proprietatea ![]() derivate
derivate
b) Orice functie continua pe un interval ![]() admite
primitive pe
admite
primitive pe ![]()
c) Daca ![]() si
si
![]() nu
este interval, atunci
nu
este interval, atunci ![]() nu
admite primitive pe
nu
admite primitive pe ![]()
d) Fie ![]() o
functie care admite primitive. Atunci orice functie
o
functie care admite primitive. Atunci orice functie ![]() care
difera de
care
difera de ![]() intr-o
multime finita nevida de puncte, nu are primitive.
intr-o
multime finita nevida de puncte, nu are primitive.
e)
Functia ![]() care nu are proprietatea lui Darboux, nu admite primitive.
care nu are proprietatea lui Darboux, nu admite primitive.
f)
![]() functii
care admit primitive si nu sunt continue ( continuitatea de speta a doua )
functii
care admit primitive si nu sunt continue ( continuitatea de speta a doua )
g) ![]() functii
care au proprietatea lui Darboux si nu au primitive.
functii
care au proprietatea lui Darboux si nu au primitive.
h) ![]() functii
care au primitive si ale caror patrate nu au primitive.
functii
care au primitive si ale caror patrate nu au primitive.
Observatie
![]() -
multimea functiilor continue pe I
-
multimea functiilor continue pe I
![]() -
multimea functiilor care admit primitive pe I
-
multimea functiilor care admit primitive pe I
![]() -
multimea functiilor care au proprietatea lui Darboux.
-
multimea functiilor care au proprietatea lui Darboux.
![]()
I.3. Definitii:
Def.: Fie![]() f
admite primitivee pe I daca
f
admite primitivee pe I daca![]() astfel
incat:
astfel
incat:
1) F derivabila pe I
2) ![]()
Def.: Daca![]() admite
primitive, multimea primitivelor lui f se numeste integrala nedefinita a lui f
si se noteaza
admite
primitive, multimea primitivelor lui f se numeste integrala nedefinita a lui f
si se noteaza![]()
Propozitie: Fie ![]() Daca
Daca![]() sunt
doua primitive ale functiei f, atunci
sunt
doua primitive ale functiei f, atunci![]() o
constanta
o
constanta ![]() astfel
incat
astfel
incat ![]()
I.4. Operatii
Daca![]() sunt
doua functii care admit primitive si
sunt
doua functii care admit primitive si![]() atunci
atunci
![]() si
si![]() admit
primitive si au loc relatiile:
admit
primitive si au loc relatiile: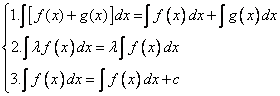
I.5. Tabel de integrale nedefinite (elementare)
(fise)
1.![]() 2.
2.![]()
3. ![]() 4.
4. ![]()
5.![]() 6.
6.![]()
7.![]() 8.
8.![]()
9.![]() 10.
10.![]()
11.![]()
(carte)
|
Functia (simpla) |
Derivata |
Domeniul de derivabilitate |
|
|
c |
R |
||
|
x |
R |
||
|
|
|
R |
|
|
|
|
cel putin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
R |
|
|
Functii (compuse) |
Derivata |
||
|
u |
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
|
||
II. Integrarea prin parti
Teorema: Daca![]() sunt
functii derivabile cu derivate continue, atunci
sunt
functii derivabile cu derivate continue, atunci![]() admit primitive pe I si sunt exprimate prin relatia:
admit primitive pe I si sunt exprimate prin relatia:
![]()
III.1 Prima metoda de schimbare de variabila
Teorema: Fie ![]() si
si ![]() functii cu proprietatile:
functii cu proprietatile:
1.![]() derivabila
pe I
derivabila
pe I
2.
f admite primitive pe J (F este o primitiva a sa). Atunci functia![]() admite
primitiva pe I, iar
admite
primitiva pe I, iar![]() este
o primitiva a lui
este
o primitiva a lui![]() de
forma:
de
forma:
![]()
Observatie:
Etape:
a)
Fie![]() care
are primitive
care
are primitive
b)
Se cauta![]() astfel
incat
astfel
incat ![]()
c)
Se cauta o primitiva![]()
d)
O primitiva a lui h este ![]() adica
adica
![]()
e)
Practic ![]() si
se diferentiaza ca o egalitate
si
se diferentiaza ca o egalitate![]() sau
sau ![]()
![]()
III.2 Primitivele functiilor rationale simple
1)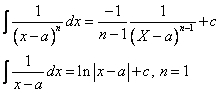
2)![]()
cazul ![]() :
: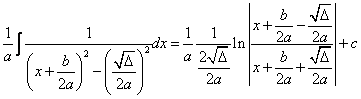
cazul ![]() :
: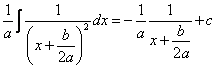
cazul ![]() :
: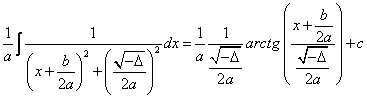
3)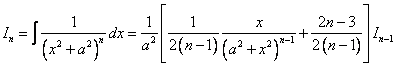
Observatie: In cazul 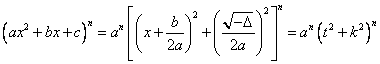
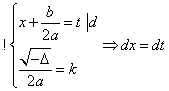
4)![]() grad
grad
![]() grad
grad![]()
a) Daca ![]() are
radacini simple:
are
radacini simple: ![]()
![]()
b) Daca ![]() are
radacini multiple:
are
radacini multiple:![]()
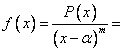
![]()
![]()
c) Daca ![]() nu
are radacini reale:
nu
are radacini reale:![]()
![]()
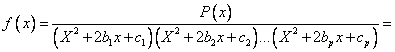
![]()
d) Daca ![]() nu
are radacini reale:
nu
are radacini reale:![]() :
:![]()
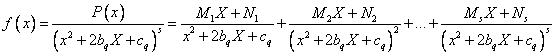
e) Daca ![]() are
in componenta descompunerile a,b,c,d atunci:
are
in componenta descompunerile a,b,c,d atunci:
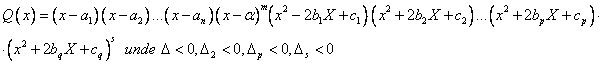
 Observatii:
Observatii:
Se determina constantele de la numarator si integram fiecare expresie in parte.
Pentru![]()
![]() ,
,![]() se
trateaza cu a,b,c,d,e (form.)
se
trateaza cu a,b,c,d,e (form.)
III.3 Primitivele functiilor rationale simple
1. ![]()
a) 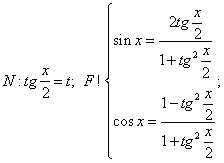
![]()
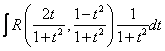
b) R impara in![]()
c) R impara in![]()
d) R para![]() ,
,
![]()
2. ![]()
3. ![]() substitutia:
substitutia:
![]()
4. ![]() substitutia:
substitutia: ![]()
5. ![]()
![]()
6. ![]()
![]()
7. ![]()
![]()
![]() Substitutie:
Substitutie: ![]()
8. 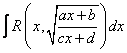
![]()
9. Substitutiile
Euler: ![]()
a. ![]()
b. ![]()
10. ![]() Substitutie:
Substitutie:![]()
11. Substitutii
pentru functii binome (Cebarsev):![]()
a. ![]()
b. ![]()
c. ![]()
12.![]() grad Q = grad P-1
grad Q = grad P-1
Coeficientii polinomului Q si![]() se
determina prin derivare si identificare.
se
determina prin derivare si identificare.
13.![]() ,
grad Q = grad P
,
grad Q = grad P
14. ![]()
![]() si
si![]() se
determina prin derivare si identificare.
se
determina prin derivare si identificare.
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2600
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2026 . All rights reserved