| CATEGORII DOCUMENTE |
| Astronomie | Biofizica | Biologie | Botanica | Carti | Chimie | Copii |
| Educatie civica | Fabule ghicitori | Fizica | Gramatica | Joc | Literatura romana | Logica |
| Matematica | Poezii | Psihologie psihiatrie | Sociologie |
TRANSFORMARI LINIARE
1. Definitia transformArilor liniare. ProprietAtile lor generale
Indisolubil legatA de notiunea de spatiu vectorial este notiunea de transformare liniarA de spatii vectoriale .
Fie V si W douA spatii vectoriale peste campul K.
Definitia 1 Se numeste
transformare liniarA (operator liniar sau morfism) de spatii vectoriale o functie
![]() cu proprietAtile
cu proprietAtile
![]() (1)
(1)
![]() (2)
(2)
Exemple
1) Trecerea la conjugat in spatiul C al numerelor complexe cu scalari reali este o transformare liniarA cAci
![]()
si pentru ![]() .
.
2)
Aplicatia nulA ![]() definitA prin relatia
definitA prin relatia ![]() pentru orice
pentru orice ![]() , este o transformare
liniarA. Intr-adevAr,
, este o transformare
liniarA. Intr-adevAr, ![]()
![]() este indeplinitA,
este indeplinitA, ![]()
![]() este indeplinitA.
este indeplinitA.
3) Aplicatia identicA ![]() este o transformare liniarA.
este o transformare liniarA.
4) DacA X este un subspatiu
al lui V, aplicatia ![]() definitA prin relatia
definitA prin relatia ![]() , este o aplicatie liniarA. intr-adevAr,
, este o aplicatie liniarA. intr-adevAr, ![]() este indeplinitA.
este indeplinitA.
AceastA aplicatie se numeste injectia canonicA a lui X in V. TransformArile liniare ale unui spatiu vectorial V intr-un spatiu vectorial de dimensiune 1 meritA o atentie deosebitA intrucat spatiul V se poate identifica cu corpul K al scalarilor. Aceste aplicatii se numesc forme liniare s-au functionale liniare definite pe V .
Teorema 1 O aplicatie ![]() este o transformare liniarA dacA si numai dacA
este o transformare liniarA dacA si numai dacA
![]() (3)
(3)
Demonstratie. Presupunem cA![]() este o transformare liniarA. Aplicand (1) si (2) gAsim
este o transformare liniarA. Aplicand (1) si (2) gAsim
![]()
Reciproc, dacA ![]() satisface conditia (2)
atunci punand
satisface conditia (2)
atunci punand ![]() deducem
deducem ![]() ; punand apoi
; punand apoi ![]() avem
avem ![]() ceea ce aratA cA
aplicatia
ceea ce aratA cA
aplicatia ![]() este liniarA.
este liniarA.
Teorema 2 DacA ![]() este o transformare liniarA atunci
este o transformare liniarA atunci
1)
![]()
2). DacA U este un subspatiu
vectorial al lui V , atunci ![]() este un subspatiu
vectorial al lui W.
este un subspatiu
vectorial al lui W.
3) DacA vectorii ![]() sunt liniar dependenti atunci si vectorii
sunt liniar dependenti atunci si vectorii ![]() sunt liniar dependenti.
sunt liniar dependenti.
Demonstratie.
1. Pentru ![]() (2) devine
(2) devine ![]()
In baza definitiei subspatiului este suficient sA arAtAm cA pentru orice
![]() si orice
si orice ![]() (corpul scalarilor
(corpul scalarilor ![]() Deoarece
Deoarece ![]() existA
existA ![]() astfel incat
astfel incat ![]() prin urmare
prin urmare ![]() (U fiind subspatiu ). Avem deci :
(U fiind subspatiu ). Avem deci :
![]()
Operatii cu transformAri liniare. Spatiul dual unui spatiu vectorial
Multimea tuturor transformArilor
liniare definite pe V si cu valori in W se noteazA cu ![]() Egalitatea transformArilor
liniare, adunarea si inmultirea cu scalari se definesc ca la functii: dacA
Egalitatea transformArilor
liniare, adunarea si inmultirea cu scalari se definesc ca la functii: dacA ![]() apartin lui
apartin lui ![]() atunci
atunci
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Teorema 3 In raport cu adunarea endomorfismelor si inmultirea lor cu scalari din K, L(V,W) este un spatiu vectorial peste campul K .
ConsecintA. Multimile L(V,V) si L(V,K) sunt spatii vectoriale peste K.
Denumiri.
a). O transformare liniarA![]() se numeste endomorfism
al spatiului V
se numeste endomorfism
al spatiului V
b). O transformare liniarA ![]() se numeste formA
liniarA.
se numeste formA
liniarA.
Cu aceste denumiri, consecinta teoremei 3. poate fi enuntatA astfel:
a). Multimea L(V,V), a endomorfismelor lui V, formeazA un spatiu vectorial peste K.
b). Multimea L(V,K), a formelor liniare definite pe V, formeazA un spatiu vectorial peste K. Acest spatiu se numeste dualul spatiului V.
Compunerea a douA transformAri liniare, definitA ca la functii, este denumitA inmultire (produs) si are ca rezultat tot o transformare liniarA. Compunerea este asociativA dar nu este si comutativA.
Operatia de compunere poate fi combinatA cu operatiile algebrice de adunare si inmultire cu scalari si avem astfel proprietAtile:
1). DacA A,B,C sunt transformAri liniare pentru care au sens A +B, AC si BC, atunci ![]()
![]()
2). DacA A,B,C sunt transformAri liniare pentru care au sens A+B, CA si C B, atunci ![]()
![]()
Teorema 4. Endomorfismele unui spatiu vectorial V formeazA un inel cu unitate necomutativ.
Fie ![]() un endomorfism al lui
V. Puterile naturale ale lui
un endomorfism al lui
V. Puterile naturale ale lui ![]() se definesc inductiv:
se definesc inductiv:
![]()
unde I este identitatea. Fie ![]() o transformare liniarA bijectivA.
o transformare liniarA bijectivA.
Inversa ![]() este tot o
transformare liniarA. In plus dacA
este tot o
transformare liniarA. In plus dacA ![]() sunt transformAri
liniare bijective atunci
sunt transformAri
liniare bijective atunci ![]() este tot o transformare liniarA bijectivA si
este tot o transformare liniarA bijectivA si ![]()
Observatie.
Teoremele 3 si 4 vor fi demonstrate folosind izomorfismele multimilor evidentiate
in enunturile teoremelor, cu spatiul vectorial ![]() respectiv cu inelul
respectiv cu inelul![]() .
.
3. Nucleul si imaginea unei transformAri liniare.
Fie U si V spatii vectoriale
peste K iar ![]() o transformare liniarA.
o transformare liniarA.
Definitia 2
Se numeste nucleu al morfismului ![]() multimea.
multimea.
![]() (7)
(7)
Nucleul lui ![]() se noteazA adesea cu
se noteazA adesea cu ![]()
Definitia 3
Se numeste imagine a morfismului ![]() multimea valorilor lui
multimea valorilor lui ![]()
![]()
Teorema 5
Fie morfismul ![]()
1). Nucleul lui![]() este un subspatiu vectorial al lui U;
este un subspatiu vectorial al lui U;
2). Imaginea lui U prin ![]() este un subspatiu
vectorial al lui V.
este un subspatiu
vectorial al lui V.
Demonstratie.
Fie ![]()
Avem deci ![]() si
si ![]() . ArAtAm
. ArAtAm ![]() Intr-adevAr,
Intr-adevAr,
![]()
deci ![]() ;
;![]() este subspatiu al lui U.
este subspatiu al lui U.
U este subspatiu
al lui U si , pe baza Teoremei 2, punctul 2, rezultA cA![]() (deci
(deci ![]() ) este subspatiu al
spatiului V.
) este subspatiu al
spatiului V.
Teorema 6 DacA ![]() este o transformare
liniarA atunci sunt echivalente urmAtoarele afirmatii:
este o transformare
liniarA atunci sunt echivalente urmAtoarele afirmatii:
1) ![]() este injectivA;
este injectivA;
2) ![]() este inversabilA;
este inversabilA;
3) ![]()
Demonstratie. Echivalenta dintre 1) si 2) este evidentA. De aceea este suficient sA demonstrAm echivalenta dintre 1) si 3).
Presupunem adevAratA relatia
![]() . ConsiderAm
. ConsiderAm ![]() si arAtAm cA x=y.
Intr-adevAr, din
si arAtAm cA x=y.
Intr-adevAr, din ![]() rezultA
rezultA ![]() deci
deci ![]() si cum
si cum ![]() rezultA x-y=0.
rezultA x-y=0.
Reciproc, dacA ![]() si
si ![]() deci
deci ![]() si cum
si cum ![]() este injectivA avem
este injectivA avem ![]() deci
deci ![]() .
.
Teorema 7 Fie ![]() o transformare liniarA. DacA V este finit dimensional ,
atunci si spatiul
o transformare liniarA. DacA V este finit dimensional ,
atunci si spatiul ![]() este finit dimensional
si
este finit dimensional
si
![]() (8)
(8)
Dimensiunea nucleului lui ![]() se numeste defectul lui
se numeste defectul lui ![]() iar dimensiunea
imaginii lui V prin
iar dimensiunea
imaginii lui V prin ![]() se numeste rangul lui
se numeste rangul lui![]() .
.
Demonstratie. ConsiderAm cA ![]() si
si ![]() DacA p=0 adicA
DacA p=0 adicA![]() rezultA
rezultA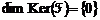 ceea ce, dupA teorema 4. este echivalent cu proprietatea cA
ceea ce, dupA teorema 4. este echivalent cu proprietatea cA ![]() este inversabilA, deci cA
este inversabilA, deci cA![]() este un izomorfism . Ori douA spatii izomorfe au aceeasi
dimensiune :
este un izomorfism . Ori douA spatii izomorfe au aceeasi
dimensiune : ![]()
Avem n = n+0 si deci relatia 3 este indeplinitA pentru p=0.
ConsiderAm cazul ![]() si baza
si baza ![]() a lui
a lui![]() pe care o completAm panA la o bazA
pe care o completAm panA la o bazA ![]() a lui V.
a lui V.
Fie
![]() (9)
(9)
Aplicand morfismul ![]() egalitatatii (9) si tinand
seama de relatiile:
egalitatatii (9) si tinand
seama de relatiile: ![]() obtinem
obtinem
![]()
Deci![]() este un sistem de generatori pentru spatiul
este un sistem de generatori pentru spatiul ![]() Dar vectorii
Dar vectorii![]() sunt liniar independenti. Intr-adevAr, presupunand cA ar
exista o relatie de dependentA liniarA nebanalA (cu cel putin un coeficient
nenul, de exemplu
sunt liniar independenti. Intr-adevAr, presupunand cA ar
exista o relatie de dependentA liniarA nebanalA (cu cel putin un coeficient
nenul, de exemplu ![]() ).
).
![]()
ar rezulta
![]()
adicA vectorul ![]() ar apartine spatiului
ar apartine spatiului ![]() Cum in
Cum in ![]() o bazA este
o bazA este ![]() am avea atunci
am avea atunci
![]()
cu ![]() adicA vectorii
adicA vectorii ![]() ar fi linar dependenti.
Contradictie cu alegerea lor (multimea aceasta a fost consideratA bazA a lui
V).
ar fi linar dependenti.
Contradictie cu alegerea lor (multimea aceasta a fost consideratA bazA a lui
V).
Astfel ![]() este o bazA a lui
este o bazA a lui ![]() si deci
si deci
![]()
4. Reprezentarea analiticA a unei transformAri liniare. Matricea transformArii
Fie ![]() si
si ![]() douA spatii vectoriale de dimensiuni finite peste campul K si o transformare
liniarA
douA spatii vectoriale de dimensiuni finite peste campul K si o transformare
liniarA ![]() . Fie
. Fie ![]() o bazA a lui V.
o bazA a lui V. ![]()
![]() Deci transformarea liniarA
Deci transformarea liniarA![]()
este datA dacA sunt
dati vectorii ![]()
Teorema 8. DacA ![]() este o bazA a lui
este o bazA a lui ![]() si
si ![]() este o bazA a lui
este o bazA a lui![]() , atunci existA o matrice si numai una
, atunci existA o matrice si numai una ![]() de tipul
de tipul ![]() astfel incat
astfel incat ![]() Mai mult, dacA
Mai mult, dacA![]() are imaginea
are imaginea
![]() (10)
(10)
atunci
![]() (11)
(11)
Notand ![]() se obtine scrierea matricealA
se obtine scrierea matricealA
![]() (12)
(12)
Demonstratie. Pentru fiecare vector ![]() j fixat, existA
coordonatele sale
j fixat, existA
coordonatele sale ![]() in raport cu baza
in raport cu baza ![]() Deci
Deci ![]()
Matricea ![]() ale cArei coloane au drept elemente coordonatele vectorilor
ale cArei coloane au drept elemente coordonatele vectorilor
![]() in raport cu baza
in raport cu baza![]() este astfel unic determinatA. Fie
este astfel unic determinatA. Fie
![]()
Tinand seama de
expresiile vectorilor ![]() avem
avem
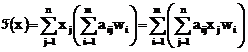
Cum pe de altA parte
![]()
gAsim
![]()
relatii care sunt tocmai cele din enunt.
A se numeste matricea
transformArii liniare ![]() in raport cu perechea de baze considerate. Vom scrie
in raport cu perechea de baze considerate. Vom scrie ![]()
Teorema 9.
Matricele A si B pAtratice de ordinul n cu elemente din K reprezintA aceeasi
transformare liniarA![]() dacA si numai dacA existA o matrice nesingularA C astfel
incat
dacA si numai dacA existA o matrice nesingularA C astfel
incat ![]() .Matricea C este matricea de trecere de la baza veche la baza
nouA.
.Matricea C este matricea de trecere de la baza veche la baza
nouA.
Demonstratie. Fie ![]() si
si![]() douA baze a lui
douA baze a lui ![]() iar C matricea de trecere de la prima bazA la a doua, adicA
iar C matricea de trecere de la prima bazA la a doua, adicA
![]() (13)
(13)
Fie ![]() o transformare liniarA. NotAm cu
o transformare liniarA. NotAm cu ![]() matricea atasatA lui
matricea atasatA lui ![]() in prima bazA adicA
in prima bazA adicA
![]() (14)
(14)
si cu ![]() matricea atasatA lui
matricea atasatA lui![]() in cea de-a doua bazA
in cea de-a doua bazA
![]() (15)
(15)
Aplicand ![]() in (12) si tinand seama de (14) obtinem
in (12) si tinand seama de (14) obtinem
![]()
Pornind de la (15) si
inlocuind pe ![]() cu expresiile lor din (13) obtinem
cu expresiile lor din (13) obtinem
![]()
Cum intr-o bazA datA a unui
spatiu vectorial coordonatele unui vector sunt unice (aici in baza ![]() ) rezultA, din cele douA expresii ale lui
) rezultA, din cele douA expresii ale lui ![]() , cA:
, cA:
![]()
sau matriceal, CB =AC de unde rezultA
![]()
MentionAm cA ![]() existA intrucat C este
presupusA nesingularA.
existA intrucat C este
presupusA nesingularA.
Exemple
1. Fie endomorfismul ![]() , unde
, unde
![]()
fatA de o pereche de
baze ![]() pe care le presupunem
ca fiind bazele canonice din
pe care le presupunem
ca fiind bazele canonice din![]() respectiv
respectiv ![]() . Endomorfismul
. Endomorfismul ![]() este dat dacA este datA
matricea sa, sugeratA prin notatia
este dat dacA este datA
matricea sa, sugeratA prin notatia ![]() .
.
Fie, de exemplu, ![]() in acest caz
endomorfismul
in acest caz
endomorfismul ![]() are matricea
are matricea
|
Politica de confidentialitate | Termeni si conditii de utilizare |

Vizualizari: 2752
Importanta: ![]()
Termeni si conditii de utilizare | Contact
© SCRIGROUP 2025 . All rights reserved