Scrigroup - Documente si articole

     

 
HomeDocumenteUploadResurseAlte limbi doc
 
Statistica


Elemente de statistica matematica utilizate la prelucrarea datelor experimentale

Statistica



+ Font mai mare | - Font mai mic



Elemente de statistica matematica utilizate la prelucrarea datelor experimentale

1.Erori de masura.



Orice proces tehnologic este caracterizat de variabile intre care exista anumite legaturi functionale (cauza-efect). Variabilele care joaca rol de cauza se numesc variabile de intrare (factori ai procesului), iar cele ce joaca rol de efect se numesc variabile de iesire (performante ale procesului).

In analiza si controlul procesului tehnologic suntem deseori nevoiti sa efectuam masurari ale anumitor performante ale procesului, pentru a preciza modul in care aceste marimi sunt influentate de diferiti factori (fig.1).

z1 z2 z3 zw


Proces tehnologic

  x1 y1

x2 y2

xk yp


Fig.1. Variabile care intervin in proces.

x , x2,.., xk Variabile de intrare - parametrii (factorii procesului): temperatura, presiune, concentratii, granulatie etc.

y , y2,.., yp Variabile de iesire - performantele procesului: productivitate, calitatea produsului, costuri de fabricatie, beneficiu, rentabilitate, grad de poluare etc.

z1, z2,.., zw Variabile de perturbatie - factori necontrolati si necomandati (factori aleatori).

Performantele procesului y1, y2,.., yp ar fi constante la valori fixate ale variabilelor de intrare x1, x2,.., xk, daca asupra procesului n-ar actiona variabilele de perturbatie z1, z2,.., zw. Actiunea permanenta si necontrolabila a acestor variabile imprima un caracter aleator (intamplator) performantelor procesului, cu alte cuvinte aceste variabile de iesire sunt tratate ca marimi aleatoare si nu ca marimi deterministe.

Rezultatul masurarii oricarei marimi este afectat de erori, acestea fiind clasificate in trei grupe:

- erori grobe (grosolane) provocate de actiunea brutala a unor factori externi cum ar fi: deteriorarea unor aparate de masura in timpul experimentarii (sau exploatarii instalatiei), realizarea incorecta a unor montaje (de regula circuite electrice: ampermetre montate in paralel, sau voltmetre montate in serie), functionarea instalatiei in regim de avarie, calificarea necorespunzatoare a personalului de exploatare etc;

- erori sistematice care apar datorita actiunii unui factor care a fost ignorat. De cele mai multe ori astfel de erori se datoresc unor neglijente in realizarea unui experiment de lunga durata, prin omiterea aducerii la "zero" (sau a recalibrarii la anumite intervale de timp) a aparaturii de masura si control;

- erori intamplatoare care sunt produse de actiunea cumulata a factorilor aleatori.

Rezultatele masurarilor afectate de erori grobe nu pot fi utilizate, ele fiind excluse din setul de observatii, in schimb rezultatele afectate de erori sistematice pot si vor fi folosite dupa corectarea acestora (prin eliminarea erorii).

Orice rezultat experimental, neafectat de o eroare groba sau eroare sistematica este afectat, totusi, de erori intamplatoare.

Aceste erori pot fi puse in evidenta prin repetarea experimentului (sau prin fixarea conditiilor de lucru ale instalatiei), stiut fiind faptul ca astfel de erori au o distributie Student, sau o distributie normala daca numarul de determinari repetate (paralele) este suficient de mare (n >

Exemplul 1.

Se elaboreaza un aliaj pe baza de Al si se cere sa se stabileasca, pe baza a opt probe (determinari paralele) continutul mediu de Al in aliaj si eroarea maxima aferenta acestui continut. Rezultatele analizelor sunt urmatoarele (%Al):

y

y

y

y

y

y

y

y

Volumul probei (date paralele):

Continutul mediu de Al in aliaj: ; .

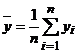Dispersia rezultatelor:    ; .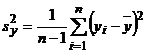

Numarul gradelor de libertate:    ; .

Prag (nivel) de semnificatie:   

Valoarea criteriului Student: (tabele statistice)

Eroarea de determinare a valorii medii:

;

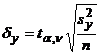Continut de Al in aliaj:    ;

Se admite cu o probabilitate de 95% ( eroare sau risc 5% - ) ca aliajul are un continut de Al in limitele: 76,312

Intervalul dintre 76,312 si 76,781 de lungime se numeste intervalul de incredere al valorii medii: el reprezinta intervalul in care se afla continutul mediu de Al (continut necunoscut) cu o probabilitate de 95%.

Intervalul de incredere se micsoreaza (creste precizia) daca numarul de determinari paralele (n) creste. Acest lucru se poate constata usor reluand exemplul anterior pentru valori diferite ale lui n: n = 2,3,.,8.

n = n ta n 0,259; d

n = n ta n 4,303; 0,186; d

n = n ta n 3,182; 0,140; d

n = n ta n 2,776; 0,135; d

n = n ta n 2,571; 0,109; d

n = n ta n 2,447; 0,092; d

n = n ta n 2,365; 0,079; d

Exemplul 2.

Intr-un laborator se efectueaza zilnic analize privind continutul de metal A din diferite materiale utilizate in procesul tehnologic. In acest scop se iau n = 2 3 probe din fiecare material si se determina doua caracteristici statistice care prezinta importanta: valoarea medie - - (calculata ca medie aritmetica) si dispersia - - (vezi exemplul 1).

Intr-un interval de 2-3 luni se pot acumula N = 40 60 de date privind valorile dispersiilor a caror medie (s2) poate fi utilizata pentru determinarea erorii dy cu o mai mare precizie, deoarece distributia erorilor poate fi considerata normala si nu Student ca in exemplul anterior.

a) Se calculeaza dispersia medie (s2) cu relatia

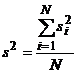
daca dispersiile au aceleasi grade de libertate: n n nN = n-1 (cazul I),

sau cu relatia

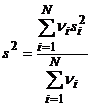
daca dispersiile au grade de libertate diferite (cazul II),

b) Se calculeaza eroarea dy cu relatia

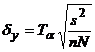; Ta = T 1,96 ( distributia normala)    (cazul I),

sau cu relatia

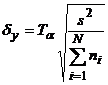(cazul II).

Obs. Eroarea dy din acest exemplu este mai mica decat eroarea dy din exemplul anterior, cand in calcule s-a folosit distributia Student si nu distributia normala (Gauss).

2.Valori anomale

Rezultatele masurarilor afectate de erori grobe sunt considerate rezultate anomale; intr-un sir ordonat (crescator sau descrescator) de valori obtinute prin determinari paralele, o astfel de valoare se plaseaza la unul din capetele sirului.

Deoarece astfel de valori trebuie excluse din setul de observatii, micsorandu-se astfel precizia determinarilor, este normal ca decizia de a considera un rezultat ca fiind anomal sa fie adoptata doar ca rezultat al testarii statistice a acesteia.

Exemplul 3.

Se realizeaza un proces de rafinare electrolitica a unui metal A si se supun analizei sapte probe prelevate din depozitul catodic pentru a se stabili continutul mediu de impuritate B, %:

y

y

y

y

y

y

y

Aceste date sunt aranjate in ordine crescatoare obtinandu-se urmatorul sir:

0,034

0,038

0,039

0,041

0,045

0,061

Deoarece 0,061 este mult diferita de celelalte valori din sir se supune testarii pentru a se stabili daca este sau nu valoare anomala, folosindu-se in acest scop criteriul rmax(min) sau Q (daca numarul de determinari paralele este relativ mic: n

Criteriul rmax(min

- valoarea medie: ; dispersia: ;

- se utilizeaza relatia: ;

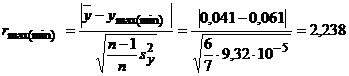- valoarea tabelata a criteriului: se compara cu valoarea calculata si deoarece rmax(min) > rT valoarea testata 0,061 se considera anomala si va fi eliminata din setul de date;

- se recalculeaza valoarea medie: si dispersia: care vor putea fi utilizate in calculele ulterioare.

Criteriul Q

- se determina amplitudinea datelor (W) cu relatia: W = ymax - ymin = 0,029;

- se calculeaza raportul Q : ( este diferenta

dintre valoarea presupusa anomala si valoarea din imediata vecinatate);

- valoarea tabelata a criteriului Q : se compara cu valoarea calculata Qc ; deoarece Qc > QT marimea testata 0,061 se considera anomala si va fi eliminata din setul de date.

Compararea dispersiilor si a valorilor medii

In rezolvarea multor probleme practice solutia se obtine prin compararea unor dispersii sau/si valori medii.

Exemplul 4

Continutul de Cu dintr-un concentrat este determinat cu ajutorul unui polarograf A rezultatele analizelor - 10 probe prelevate - fiind urmatoarele:

y

y

y

y

y

y

y

y

y

y

% Cu

Pentru modernizarea activitatii in laboratorul de analize se propune inlocuirea vechiului polarograf A cu un polarograf mai nou B, rezultatele analizelor - 10 probe prelevate - fiind urmatoarele:

y

y

y

y

y

y

y

y

y

y

% Cu

Rezolvare

Problema se reduce la compararea dispersiilor datelor furnizate de cele doua polarografe.

Polarograf A: n = 10; ; .

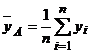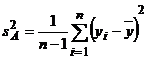; nA = n- .

Polarograf B: n = 10; ; .

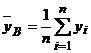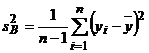; nB = n- .

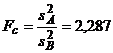Se calculeaza raportul dispersional

( se calculeaza astfel incat Fc sa fie supraunitar)

si se compara cu valoarea tabelata a criteriului F (Fischer): .

Deoarece Fc < FT se considera ca diferentele dintre dispersii sunt provocate de factorii aleatori si nu de caracteristicile noului polarograf; desi (din punct de vedere algebric), cele doua dispersii se considera egale statistic: cu alte cuvinte, din punct de vedere al preciziei cele doua polarografe sunt echivalente si deci nu este oportuna inlocuirea polarografului A cu polarograful B.

Exemplul 5

Randamentul unei instalatii metalurgice in conditii de functionare standard (A) are urmatoarele valori, %:

y

y

y

y

y

(A)

(nA = 5 - date paralele)

Pentru imbunatatirea performantei instalatiei s-a considerat necesar sa se modifice unul din parametrii de functionare ai acesteia, obtinandu-se in aceste conditii (B) urmatoarele rezultate, %:

y

y

y

y

(B)

(nB = 4 - date paralele)

Se cere sa se stabileasca daca modificarea regimului de functionare are sau nu efect pozitiv asupra randamentului.

Rezolvare

Problema consta in compararea valorilor medii ale randamentului y(A) si y(B) pentru cele doua situatii (A) si (B): daca cele doua medii sunt egale statistic chiar daca algebric nu sunt egale se considera ca modificarea regimului de functionare nu are efect pozitiv asupra randamentului, iar daca mediile nu sunt egale statistic se admite ipoteza ca modificarea regimului de functionare are efect pozitiv asupra randamentului.

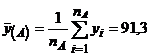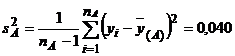(A)    ; ; nA = nA -

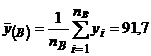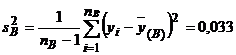(B); ; nB = nB -

Cu ajutorul criteriului Fischer (F) se verifica daca cele doua dispersii sunt egale statistic, deoarece, numai in acest caz se poate trece la compararea celor doua medii y(A) si y(B)

; ;

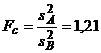Deoarece Fc < FT se admite ca cele doua dispersii sunt egale statistic si se calculeaza o dispersie medie

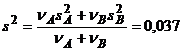; n nA nB

care va fi utilizata in testul Student (t) pentru compararea valorilor medii

;

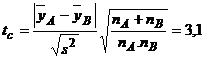Se constata ca tc > tT si in concluzie se apreciaza ca cele doua medii nu sunt egale statistic; cu alte cuvinte modificarea regimului de functionare are efect pozitiv asupra randamentului.

Exemplul 6

Pentru a stabili influenta microalierii (cu elementul K) asupra duritatii unui aliaj special s-a efectuat un experiment pe schema analizei dispersionale. In acest scop s-au elaborat m = 6 aliaje cu continuturi diferite de K, s-au prelevat cate n = 3 probe din fiecare aliaj si s-au facut determinari ale duritatii rezultatele fiind centralizate in tabelul 1.

Tabelul 1. Determinarea influentei elementului A asupra duritatii

Adaos de K, %

Nivelul factorului

Determinari    paralele n = 3

Obs. Prin niveluri ale factorului K se inteleg valorile distincte (m = 6) pe care acesta le ia in timpul experimentarii.

Rezolvare

Aceasta este o problema complexa, pentru rezolvarea careia trebuie parcurse mai multe etape:

a) Se calculeaza sumele de patrate

; ;

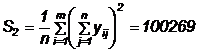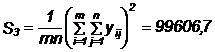
in care

S1 - este suma patratelor tuturor datelor din tabel: S1 = PVM + IFK + IFA (PVM - patratul valorilor medii, IFK - influenta factorului K, IFA - influenta factorilor aleatori);

S2 - este suma patratelor valorilor obtinute prin inlocuirea datelor din fiecare rand al tabelului prin media lor aritmetica: S2 = PVM + IFK;

S3 - este suma patratelor valorilor obtinute prin inlocuirea tuturor datelor din tabel prin media lor aritmetica: S3 = PVM.

b) Se calculeaza dispersiile corespunzatoare fiecarui nivel al factorului K

;

; ; ; ; .

c) Se verifica omogenitatea lor (daca sunt egale statistic) cu ajutorul criteriului Cochran; pentru aceasta, se calculeaza raportul Gc dintre dispersia maxima () si suma tuturor dispersiilor si se compara Gc cu o valoare critica (tabelata) GT

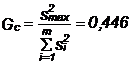; ; (a

n reprezinta numarul gradelor de libertate ale dispersiei ,n =n-1=2, iar n este numarul dispersiilor care se compara ,n = m = 6

Deoarece Gc < GT se admite, cu o probabilitate de 95% (P = 1-a) ca dispersiile sunt omogene, iar in calculele ulterioare va fi utilizata media lor aritmetica (- dispersia reproductibilitatii) care este o masura a influentei factorilor aleatori ( o masura a erorii experimentale).

; n = m(n-1)=12.

d) Se calculeaza o dispersie globala (s2) care contine atat dispersia provocata de factorii aleatori () cat si dispersia provocata de factorul analizat ()

; n = m-1

e) Cele doua dispersii ( si s2) se compara cu ajutorul criteriului Fischer

;

si deoarece Fc > FT rezulta ca microalierea cu elementul K influenteaza asupra duritatii aliajului, dispersia provocata de acest element avand valoarea

.

f) Pentru a se stabili modul in care adaosul de element K poate influenta asupra duritatii se apeleaza la criteriul de rang Duncan parcurgandu-se urmatoarele etape:

- valorile medii, corespunzatoare nivelurilor factorului K, se aranjeaza in ordine crescatoare

Nivelul 1 2 3 4 5 6

Valori medii

g) Se calculeaza abaterea medie patratica normata

.

h) Din tabelele criteriului de rang Duncan se extrag m-1 valori ale rangurilor

; ; ;

; .

i) Se determina cele mai mici ranguri semnificative (cmmrs) inmultind valorile rangurilor cu abaterea medie patratica normata

; ; ;

; .

j) Diferentele dintre medii, in numar de se compara cu cele mai mici ranguri semnificative, comparatia realizandu-se astfel:

- diferenta se compara cu cmmrsm-1,

....................

- diferenta se compara cu cmmrsm-k,

....................

- diferenta se compara cu cmmrsk-i etc.

Diferentele se considera semnificative daca depasesc valorile cmmrs la pragul de semnificatie ales (a ), rezultatele compararii fiind trecute in tabelul 2.

Tabelul 2. Compararea diferentelor dintre medii cu cele mai mici ranguri semnificative

Nr. aliajelor comparate

Diferenta dintre medii

cmmrs

Semnificatia diferentelor

Semnificativa

Semnificativa

Semnificativa

Semnificativa

Nesemnificativa

Semnificativa

Semnificativa

Semnificativa

Nesemnificativa

Semnificativa

Semnificativa

Nesemnificativa

Nesemnificativa

Nesemnificativa

Nesemnificativa

Din analiza rezultatelor compararii se desprind urmatoarele concluzii:

- aliajele 1, 2 si 3, cu continuturi de 0%; 0,4% si respectiv 0,8% K, nu se deosebesc semnificativ din punct de vedere al duritatii, cu alte cuvinte adaosurile de element K pana la 0,8% nu afecteaza sensibil duritatea;

- aliajul cu duritatea cea mai mare este aliajul nr.6 (cu 2% K) cu precizarea ca acesta nu se deosebeste semnificativ, din punct de vedere al proprietatii analizate, de aliajul nr. 5 (cu 1,6% K). Din acest motiv se recomanda ca microalierea sa se realizeze cu 1,6% K, nefiind necesare adaosuri de 2% K.


Politica de confidentialitate | Termeni si conditii de utilizare



DISTRIBUIE DOCUMENTUL

Comentarii


Vizualizari: 3015
Importanta: rank

Comenteaza documentul:

Te rugam sa te autentifici sau sa iti faci cont pentru a putea comenta

Creaza cont nou

Termeni si conditii de utilizare | Contact
© SCRIGROUP 2024 . All rights reserved