Modele experimentale fundamentate pe analiza dispersionala

1 Notiuni generale utilizate in modelarea experimentelor

Analiza dispersionala, cunoscuta si sub numele de analiza de varianta (ANOVA - Analzsis Of Variance), a fost introdusa de matematicianul R.A. Fisher. Pornind de la observatiile acumulate pe parcursul mai multor ani de experiente agrotehnice acesta a fundamentat o serie de principii si metode de programare si dirijare a experimentelor precum si de interpretare statistica a rezultatelor. Rezultatele acestei cercetarii au fost sintetizate in doua lucrari de referinta chiar si astazi: "Statistical Methods for Research Workers" - 1925 si "The Design of Experiments" - 193

Demersul stiintific al acestuia a pornit de la compararea productiilor medii ale unor suprafete de teren cultivate cu diferite soiuri de cerale sau plante tehnice. Aceste suprafete erau supuse unor tratamente diferentiate (de exemplu: adancimea araturii, cantitatea si periodicitatea irigarilor sau a igrasamintelor folosite).

Metodele puse la punct de Fisher s-au concretizat ulterior in modele experimentale ce si-au gasit utilitatea in diverse domenii ca: industrie (testarea unor prorotipuri sau tehnologii), comert (impactul unor campanii publicitare), medicina (fundamentarea diagnosticului si estimarea efectului tratamentelor aplicate), mediu (impactul asupra mediului a factorilor poluanti sau al tehnologiilor de depoluare), agricultura (efectul diferitelor proceduri de tratare/cultivare a solurilor asupra productiei medii obtinute sau in procesul de obtinere a soiurilor superioare), etc.

"In general se considera ca experimentul este acea metoda de cercetare prin care variatia (modificarea) uneia sau mai multor variabile explicative (independente) este controlata sau "manipulata" de cercetator, masurandu-se apoi efectul acesteia asupra variabilei (variabilelor) rezultative (efect)"[1].

Pornind de la aceasta definitie vom cauta sa explicitam termenii utilizati.

Variabile rezultative. Sunt variabile dependente a caror transformare este masurata in cadrul experimentului. Deoarece esenta medodei de analiza dispersionala consta in compararea mediilor este obligatoriu ca acestea sa fie variabile cantitative.

Variabile explicative. Sunt variabile independente ce constituie factorii cauzali ce produc modificari asupra variabilei dependente explicative. Acestea pot fi:

• cantitative (temperatura, valori ale unor analize medicale obtinute din laborator, umiditate, etc.) ;
• calitative (sex, mediu de provenienta, studii, tip de sol, etc.).

Considerand experimentul ca un sistem putem clasifica variabilele independente astfel:

• endogene (variabile controlate / manipulate in cadrul esperimentului);
• exogene (din afara sistemului analizat, care nu sunt supuse experimentarii si a caror influenta se poate interfera cu cea a variabilelor rezultative ducand la reducerea performantelor de fidelitate a modelului experimental.

In functie de conditiile de desfasurare a experimentului putem intalnii urmatoarele situatii:

• Experimentul are loc intr-un sistem inchis. Experimentatorul poate mentine la un nivel constant toate variabilele exogene. O astfel de situatie poate fi usor reprodusa in domeniul tehnic (fizica, chimie, etc.)
• Experimentul are loc intr-un sistem deschis. In cazul proceselor din sfera economica sau sociala controlul efectiv al variabilelor exogene este imposibil de realizat. In consecinta, in aceasta situatie se va efectua un control de natura statistica, prin aplicarea unui procedeu de selectie aleator, pentru a forma esantioanele supuse experimentului.

Dupa scopul urmarit se disting urmaroarele tipuri de experimente:

• Preliminare. Se urmareste testarea unui numar mare de factori (tratamente) pentru a avea informatii in vederea proiectarii cercetarilor ulterioare;
• Critice. Se compara rezultatele diferitelor tratamente pentru a le putea identifica pe cele care au o influenta semnificativa;
• Demonstrative. Se testeaza unul sau mai mulste tratamente in raport cu un etalon fixat anterior.

Dupa numarul variabilelor explicative experimentele pot fi unifactoriale sau multifactoriale.

In figura 1 este prezentata schema decizionala de alegere a modelului de analiza dispersionala in functie de numarul variabilelor factoriale si modul in care au fost selectate esantioanele.

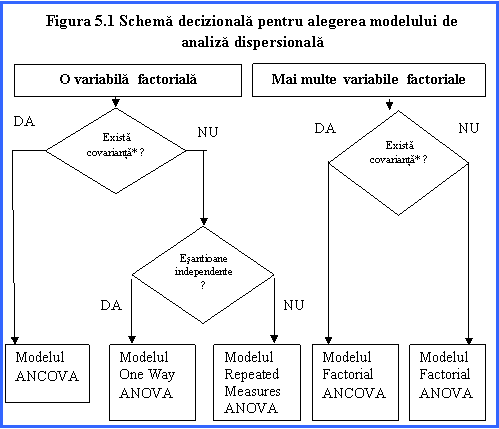
o variabila nominala ce influenteaza variabila dependenta

Modelul de analiza dispersionala unifactoriala.

One-Way ANOVA

Cu ajutorul testului parametric de analiza dispersionala ANOVA se pot examina doua sau mai multe esantioane independente pentru a determina daca mediile populatiilor din care provin ar putea fi egale, putandu-se pune astfel in evidenta influenta factorului considerat sau a tratamentului efectuat.

Practic populatiile se pot clasifica utilizand un singur criteriu, numit factor (tratament) dupa cum se poate observa in figura nr. 2. Fiecare populatie este determinata de un nivel al factorului (sunt k niveluri).

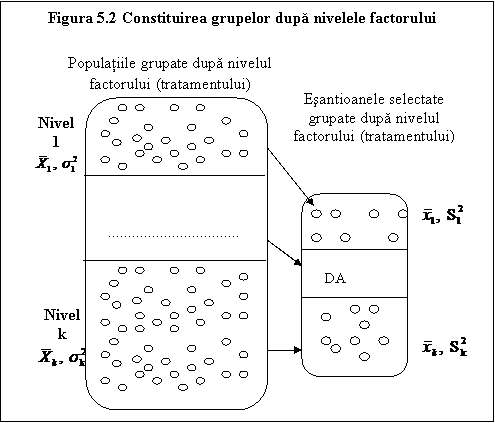
Ipoteza nula si ipoteza alternativa:

H₀: pentru j=1,.,k

H₁: astfel incat

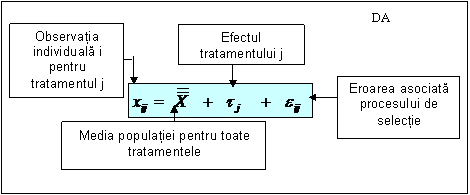
Fiecare observatie individuala, considerata ca suma a trei componente separate, poate fi descrisa in termenii modelului 1.

In concordanta cu acest model fiecare observatie (x_ij) asociata tratamentului j este suma componentelor: media populatiei pentru toate tratamentele, efectul tratamentului j si eroarea de esantionare. In acest context ipotezele pot fi reformulate astfel:

H₀: t_j=0 pentru orice j=1,.,k

H₁: t_j 0 pentru cel putin unul dintre j=1,.,k.

Daca efectul fiecarui tratament t_j pentru orice j=1,.,k este nul, media fiecarei populatii este egala cu media totala.

Model 1

Utilizarea testului parametric ANOVA pleaca de la urmatoarele premize:

Esantioanele au fost selectate independent;

Dispersiile populatiilor sunt egale ();

Populatiile sunt normal distribuite.

Aceste conditii (in special cea privind egalitatea dispersiilor) sunt foarte importante. Daca nu sunt indeplinite se va utiliza testul neparametric Kruskal-Wallis pentru a compara tendinta centrala a doua sau mai multe esantioane independente.

In realitate ANOVA este un procedeu robust, adica neafectat major de neindeplinirea unei conditii, cu exceptia celei cu privire egalitatea dispersiilor,

Pentru efectuarea testului este necesara calcularea variatiei pe surse de provenienta astfel:

Tabel nr. 1

Variatia dintre grupuri (SSB) reflecta variatia dintre mediile esantioanelor si media generala. Variatia reziduala (SSE) se calculeaza pornind de la abaterile valorilor observate si mediile fiecarui grup. Pentru ca cale doua tipuri de variatie sa fie comparabile in vederea realizarii testului statistic este necesara corectarea acestora cu numarul corespunzator de grade de libertate.

Testul statistic este dat de relatia:.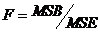

Testul se realizeaza unilateral dreapta si pentru un anumit nivel de siguranta a se respinge ipoteza nula daca valoarea calculata F este mai mare decat cea teoretica, corespunzatoare nivelului de semnificatie ales si numarului de grade de libertate df₁ si df₂.

Tinand cont de ipoteza egalitatii dispersiilor populatiilor, intervalul de incredere pentru estimarea mediilor esantioanelor este dat de relatia:

unde S_p= estimatia abaterii standard in populatii;

n_j= numarul de elemente ce formeaza esantionul j;

= media esantionului j;

t= valoarea distributiei t corespunzatoare nivelului de semnificatie ales si numarului de grade ce libertate asociat variatiei din interiorul grupurilor.

In cazul in care se compara mediile din doua esantioane testul ANOVA unifactoriala si testul Student realizat pe baza dispersiei estimate sunt echivalente. Ambele testeaza ipoteza egalitatii mediilor a doua populatii pe baza datelor din doua esantioane independente si pornesc de la premiza egalitatii variantelor celor doua populatii, utilizand o estimatie a acesteia.

2.1. Tematici avansate in ANOVA. Comparatiile perechi

Chiar daca in urma aplicarii testul de analiza dispersionala ANOVA se respinge ipoteza egalitatii mediilor, exista posibilitatea pentru anumite subseturi diferentele dintre medii sa nu fie semnificative statistic.

Metoda comparatiilor perechi este precedata intotdeauna de ANOVA si are sens aplicarea ei doar in situatia in care valoarea testului F din tabelul de analiza a variatiei duce la acceptarea ipotezei alternative conform careia nu toate mediile grupurilor sunt egale. Ne punem intrebarea: Care sunt mediile diferite? Am putea efectua testele pentru verificarea mediilor a doua esantioane independente comparand pe rand grupul 1 cu grupul 2, grupul 1 cu grupul 3, etc. Am avea de efectuat k(k-1)/2 comparatii pentru verificarea ipotezelor.

Problematica metodei comparatiilor perechi porneste in mod uzual de la stabilirea nivelului de semnificatie al experimentului (a) si al familiei comparatiilor multiple ce trebuiesc efectuate (a_F). Pentru fiecare verificare de ipoteza probabilitatea aparitiei erorii de tip I este a. Probabilitatea ca o eroare de tipul I sa apara undeva in lista comparatiilor multiple este a_F si se numeste nivel de semnificatie global.

In continuare sunt prezentate cateva metode de realizare a comparatiilor multiple pentru un grup de medii.

Tukey's Honestly Significant Differences

Testul Tukey este prima metoda care a abordat problematica realizarii comparatiilor multiple in urma efectuarii testului ANOVA:

Consideram variabilele normal repartizate si cu dispersiile egale, provenite din esantioane independente X_j~N() unde j=1,..,k; k reprezentand numarul esantioanelor de volum n. S² reprezinta estimatia nedeplasata a dispersiei s bazata pe numarul gradelor de libertate df. Deci, aplicarea acestui test, trebuie sa urmeze unui test de verificare a egalitatii dispersiilor .

H₀: pentru j=1,.,k

H₁: astfel incat

Se observa ca ipoteza H₀ este echivalenta cu multimea tuturor ipotezelor:

H_0(ij): (i j, 1 i,j k). Aceasta ipoteza este acceptata daca:

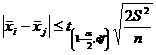unde reprezinta mediile selectiilor.

Acest lucru inseamna ca pentru oricare doua valori i si j ipoteza poate fi verificata utilizand testul Student. Deoarece H₀ este echivalenta cu multimea ipotezelor H_0(ij): (i j, 1 i,j k), o putem verifica luand intersectia tuturor celor regiuni de acceptare si o acceptam daca se verifica relatia:

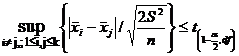sau daca: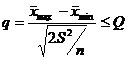

unde Q este cuantila de ordinul 1-a a amplitudinii studentizate cu df grade de libertate.

Sub aceasta forma testul poate gasi semnificatie a diferentelor pentru mediile cu valori indepartate chiar daca pe ansamblul tuturor mediilor nu exista o semnificatie a diferentelor. In aceasta situatie se recomanda utilizarea testului Tukey modificat precedata de realizarea unei analize dispersionale. Chiar daca s-a acceptat sau nu ipoteza egalitatii mediilor acest procedeu de testare nu permitea sa se precizeze intre care dintre cele k medii sunt diferente semnificative.

Testul Tukey presupune calcularea unei statistici proprii de forma: . Valoarea q se extrage din tabela cu valorile critice ale testului Tukey pentru nivelul de semnificatie ales, k numarul de esantioane pentru care se face comparatia si df2 numarul de grade de libertate pentru variatia din interiorul grupurilor (determinata de procesul de esantionare) din tabelul ANOVA.

Valoarea este data de relatia in care MSE este media variatiei din interiorul grupurilor (tabelul ANOVA) iar n reprezinta volumul selectiilor.

Valoarea w este o diferenta limita pentru nivelul de semnificatie ales. Orice diferenta dintre mediile esantioanelor mai mare decat w este semnificativa.

In cazul in care volumele esantioanelor difera se calculeaza valoarea in care s este abaterea standard totala. Apoi, comparatia se realizeaza pe perechi. Pentru fiecare pereche i,j se calculeaza 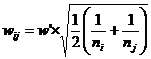. Daca diferenta dintre mediile si este mai mare decat valoarea critica w_ij se considera semnificativa.

Inegalitatea lui Bonferroni

Este considerata o metoda simpla si poate fi utilizata in orice situatie atunci cand efectuam comparatii multiple si dorim sa controlam nivelul de semnificatie global.

Verificam ipoteza pentru testul T₁ utilizand nivelul de semnificatie a , Testul T₂ cu nivelul de semnificatie a si asa mai departe pana la testul T_g cu nivelul de semnificatie a_g. Probabilitatea de producere a unei erori te tipul I la oricare comparatie din lista este α₁+α₂++α_g.

De exemplu daca dorim sa comparam mediile a 5 esantioane independente avem nevoie de 5x45x4/2 = 10 teste de verificare a ipotezei egalitatii mediilor. Daca dorim sa mentinem nivelul de semnificatie global comparatiilor a 10% vom efectua fiecare test individual pentru un nivel de semnificatie de 1%.

Algoritmul de aplicarea inegalitatii lui Bonferroni este:

1.Se calculeaza g, numarul de comparatii ce trebuie efectuate. Pentru k esantioane independente g=k(k-1)/2

2. Se alege a_F nivelul de semnificatie global al comparatiilor. In mod uzual se ia 10% exceptand situatiile in care numarul de esantioane independente este mic (2 or 3).

3. Se calculeaza nivelul de semnificatie al fiecarui experiment a a_F / g

4. Se efectueaza comparatii pentru mediile grupurilor luate doua cate doua. Decidem ca exista diferenta semnificativa statistic intre mediile grupului i si j daca :

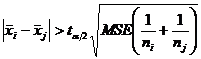sau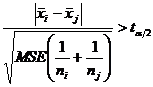

Numarul de grade de libertate necesare pentru a stabili valoarea teoretica t_a conform repartitiei Student se preia din tabela ANOVA (este notat df2 si este valoarea utilizata la calcularea MSE).

2.2 Postulatele ANOVA si remediile posibile in cazul nerespectarii acestora

Dupa cum s-a precizat la paragraful 2, efectuarea testului de analiza dispersionala ANOVA presupune respectarea unor premize majore si anume: esantioanele au fost selectate independent; populatiile sunt normal distribuite si dispersiile populatiilor sunt egale.

Ipoteza independentei esantioanelor

Prin esantioane independente se intelege ca procedeul de selectie al unui esantion nu este asociat cu procedeele de selectie ale celorlalte. Aceasta premiza este usor de verificat prin analiza modului in care au fost selectate elementele esantioanelor. Exemple de esantioane formate din observatii dependente: cele utilizate in studii de tipul inainte si dupa aplicarea unui tratament, esantioane de tip panel si observatii pereche.

Spunem ca observatiile sunt independente atunci cand nu exista corelatie intre variabilele independente si intre componentele reziduale.

In cazul in care nu este respectat acest postulat, chiar daca estimatorii obtinuti nu sunt deplasati eroarea standard este eronata.

Independenta esantioanelor este testata cu ajutorul testului Durbin-Watson. Statistica testului este data de relatia:

unde reprezinta coeficientul de corelatie dintre observatiile x₁ si x₂ pentru care se verifica independenta.

Valoarea calculata d este cuprinsa in intervalul [0,4] iar interpretarea acesteia se face sub urmatoarea forma:

daca valoarea obtinuta este apropiata de 0 ne indica existenta unei autocorelatii pozitive, eroarea standard obtinuta fiind eronata in sensul diminuarii acesteia;

daca valoarea obtinuta este apropiata de 4 ne indica existenta unei autocorelatii negative, eroarea standard obtinuta fiind eronata in sensul exagerarii acesteia;

daca valoarea obtinuta este apropiata de 2 nu exista autocorelatie.

daca valoarea obtinuta este intre 1,5 si 2,5 se accepta ipoteza independentei observatiilor.

Remediile posibile in cazul dependentei observatiilor sunt:

cautarea unui factor neluat in consideratie caruia sa i se atribuie covariatia existenta;

in cazul in care nu poate fi gasit un astfel de factor se recomanda fie utilizarea unui alt model de analiza (random effects models pentru date longitudinale) fie transformarea variabilelor dependente utilizand coeficientul de corelatie.

Ipoteza normalitatii distributiilor

Aceasta poate fi usor verificata prin analizarea histogramei sau a graficului probabilitatilor normale, realizat de majoritatea programelor statistice. Cand analiza graficelor este neconcludenta se recomanda utilizarea unuia din urmatoarele teste (prezentate pe larg in paragraful XXX):

Shapiro-Wilks (W test).Acesta este considerat testul standard de verificare a normalitatii si este recomandat pentru esantioane de volum redus si mediu;

Testul χ² este recomandat in cazul esantioanelor de volum mare;

Testul Kolmogorov-Smitnov sau Testul K-S cu aplicarea corectiei Lilliefors se aplica tot in cazul esantioanelor de volum mare. Daca datele sunt grupate pe intervale aceste teste sunt preferate testului χ² .

Consecintele nerespectarii acestei ipoteze sunt:

O larga deviere de la normalitate duce la scaderea puterii si eficientei acelor teste de semnificatie care pornesc de la aceasta conditie;

In situatia in care dimensiunile esantioanelor sunt diferite, orice deviere de la normalitate este amplificata;

In cazul in care esantioanele sunt de volum normal (n>50) verificarea normalitatii distributiilor nu mai este foarte importanta deoarece, conform Teoremei limitei centrale, esantioanele de volum normal aproximeaza distributia normala.

In cazul nerespectarii acestui postulat, pentru evitarea consecintelor mai sus enumerate se recomanda fie transformarea datelor fie utilizarea testelor neparametrice alternative (de exemplu testul Kruskal-Wallis) . Decizia transformarii datelor trebuie realizata insa cu prudenta deoarece poate produce schimbari ale relatiilor de legatura intre variabilele dependente si cele independente.

Ipoteza egalitatii dispersiilor

Este considerata cea mai importanta conditie. Exista mai multe metode de verificare a omogenitatii dispersiilor (HOV-Homogeneity of Variance). In paragraful 3.2.3 sunt prezentate pe larg testele statistice cu ajutorul carora se poate verifica aceasta ipoteza.

Se cunoaste faptul ca daca postulatul egalitatii variantelor nu este indeplinit rezultatele ANOVA sunt neconcludente.

In cazul in care nici ipoteza normalitatii distributiilor nu este respectata se recomanda transformarea datelor in vederea normalizarii acestora si stabilizarii variantelor. Daca acestea raman neomogene se vor utiliza teste neparametrice.

In schimb, daca ipoteza normalitatii distributiilor este acceptata exista posibilitatea aplicarii unei corectii. Metoda este intalnita sub denumirea Welch's ANOVA.

Acesta se realizeaza in ipoteza independentei celor k esantioane selectate din populatii normal distribuite de medie μ_i si dispersie . Estimatorii parametrilor pentru esantionul i sunt determinati dupa relatiile:

si

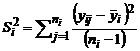
Numarul total de observatii este iar media pe total.

Se definesc ponderile . Pe baza lor se va putea calcula estimatorul ponderat al mediei pe total conform relatiei:

Deoarece dispersiile esantioanelor nu se cunosc pentru ponderile w_i se vor utiliza estimatorii acestora: relatia estimatorului ponderat al mediei pe total devenite:

In cazul in care se cunosc dispersiile , varianta dintre grupuri ar putea fi masurata prin varianta explicata ponderata conform relatiei:

Estimatorul acesteia este

Consideram    f_i numarul de grade de libertate al esantionului i si notam:

Statistica testului Welch este: 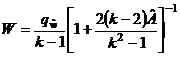(relatia 1)

Valoarea calculata se compara cu valoarea teoretica a distributiei F_v1,v2 pentru nivelul de semnificatie ales unde v₁ =k-1 iar v₂ =.

3. Modelul de analiza dispersionala unifactoriala realizat pe esantioane dependente (Repeated Measures ANOVA)

Metoda se bazeaza pe modelul de analiza a variatiei cu masuratori repetate. In aceasta situatie fiecare unitate este studiata pentru fiecare tratament aplicat. Unitatile formeaza blocuri si pentru fiecare unitate dintr-un bloc se produc masuratori la aplicarea fiecarui tratament.

Modelele cu masuratori repetate sunt frecvent utilizate in cercetarea fenomenelor economica sociale cand se obtin informatii repetate de la acelasi esantion numit panel.

Avantajele modelelor cu masuratori repetate

Variabilitatea inter unitati este exclusa din variatia reziduala ceea ce face mai usoara compararea tratamentelor;

Fiecare unitate serveste pentru propriul control;

Reducerea costurilor. Odata facute cheltuielile necesare esantionarii acestea nu se vor mai efectua pentru cercetarile ulterioare realizate pe baza aceluiasi esantion

Dezavantajele modelelor cu masuratori repetate

• Exista o perioada de asteptate intre tratamente care poate determina aparitia fenomenelor:

de acumulare (in cazul tratamentelor chimice ale solurilor in agricultura);

de invatare (in cercetarile sociale indivizii dobandesc anumite cunostinte din cercetarile anterioare);

de imunizare sau dependenta (in medicina)

• Exista riscul ca raspunsurile sa nu mai fie spontane, ele devenind rezultatul unei rutine sau fiind conditionate de raspunsurile anterioare la intrebarile similare.

Datele pot fi sistematizate intr-un tabel de forma urmatoare:

Cu toate ca putem controla si blocurile, preocuparea principala este legata de testarea egalitatii mediilor pentru toate tratamentele (esantioanele). In consecinta formularea ipotezelor este urmatoarea:

H₀: pentru j=1,.,k;

H₁: astfel incat

Ca si in cazul ANOVA unifactoriala, fiecare observatie individuala este considerata ca suma a unor componente separate ce poate fi descrisa in termenii modelului 2.

Model 2

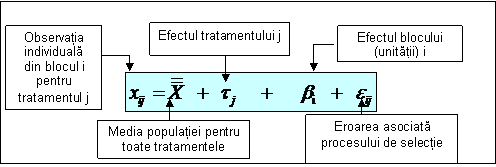
In acest model fiecare valoare x_ij asociata blocului i si tratamentului j este suma urmatoarelor elemente: media populatiei pentru toate tratamentele (esantioanele), efectul tratamentului j (t_j), efectul blocului i (b_i) si eroarea de esantionare (e_ij). In acest context ipotezele pot fi reformulate astfel:

H₀: t_j=0 pentru orice j=1,.,k

H₁: t_j 0 pentru cel putin unul dintre j=1,.,k.

Daca efectul fiecarui tratament t_j pentru orice j=1,.,k este nul, media fiecarei populatii este egala cu media totala.

In cazul acestei metode exista o singura observatie x_ij pentru fiecare combinatie bloc-tratament. Se poate considera ca fiecare din aceste combinatii reprezinta un esantion format dintr-o singura unitate.

Utilizare metodei blocurilor randomizate pleaca de la urmatoarele premize:

• Variabila independenta este nominala;
• Esantioanele sunt dependente (datele sunt culese in urma u ui plan de masuratori repetate);
• Variabila dependenta este masurata pe scala cardinala sau proportionala;
• Pentru fiecare tratament variabila dependenta urmeaza o distributie normala sau aproximativ normala;
• Dispersiile valorilor x_ij sunt egale pentru fiecare tratament j=1,.,k. Aceasta este prezumtia de sfericitate si este echivalenta cu cea de omogenitate a dispersiilor pentru modelul ANOVA;
• Nu exista o interactiune intre blocuri si tratamente. Conform metodei blocurilor randomizate prezenta unei interactiuni ar fi atunci cand efectul tratamentului depinde de blocul unde urmeaza sa fie administrat.

Pentru efectuarea testului este necesara calcularea urmatoarelor tipuri de variatie:

Tabel nr. 2

Testul statistic este dat de relatia:.

Ca si in catul testului ANOVA unifactorial MSB reprezinta variatia dintre mediile tratamentelor (esantioanelor) iar MSE reprezinta variatia din interiorul esantioanelor. Este un test unilateral dreapta iar valoarea calculata se compara cu valoarea critica pentru un nivel de semnificatie dat (a) si numarul de grade de libertate df₁=k-1 si df₂=(k-1)(b-1). Daca valoarea calculata este mai mare decat valoarea critica se respinge H₀ si se accepta H₁.

4 Utilizarea modelelor de analiza dispersionala sub SPSS

Primul pas in efectuarea unui test statistic pentru compararea mediilor a doua grupuri il reprezinta alegerea optiunii potrivite in functie de modul in care au fost selectate esantioanele.

A)    Esantioane independente. One-Way ANOVA

Daca avem doua sau mai multe esantioane independente vom alege metoda adecvata din submeniul de comparare a mediilor urmand urmatoarea cale: Analyze/Compare Means/ One-Way ANOVA. Dupa selectarea testului se deschide fereastra de definire a acestuia (figura nr. ) care ne permite in zona Dependent List selectarea variabilei/variabilelor pentru care dorim sa efectuam testul.

In fereastra Factor se trece variabila in functie de care se formeaza grupurile pentru care dorim sa testam semnificatia diferentelor.

In situatia in care se vor trece mai multe variabile dependente se va returna pentru fiecare din ele un tabel cu rezultatele aplicarii testului ANOVA. Fiecare variabila din lista trebuie sa fie masurata pe scala de interval sau proportionala, trebuie sa urmeze o repartitie normala sau aproximativ normala. Conditia de normalitate a distributiei este foarte important sa fie respectata doar in cazul esantioanelor de volum redus.

Inainte de efectuarea testului este obligatorie verificarea respectarii prezumtiei egalitatii variantelor. Prin activarea butonului de comanda Options se deschide fereastra One-Way ANOVA Options (figura ) de unde putem activa efectuarea testarii omogenitatii variantelor.

Pentru exemplificare s-a selectat din baza de date variabila dependenta "nota acordata utilitatii practice a cursurilor" si variabila factoriala "Facultatea".

Figura 3 Fereastra de definire a testului One-Way ANOVA

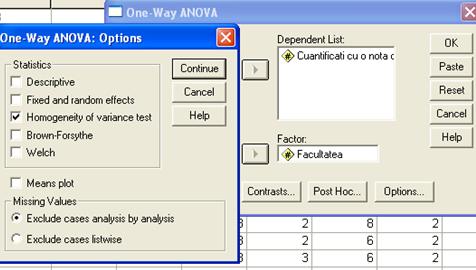
Prin butonul OK se comanda procesarea testului, obtinandu-se outputurile din tabelele 3 (rezultatele efectuarii testului Levene pentru verificarea omogenitatii variantelor) si 4 (rezultatele testului de analiza dispersionala unifactoriala ANOVA).

Tabel 3

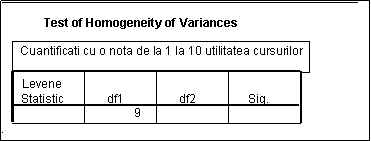
Interpretarea outputului din tabelul 3:

Levene Test. Valoarea calculata a a statisticii testului.

df₁ Numarul de grade de libertate k-1 unde k este numarul de grupe dupa variabila factor.

df₂ Numarul de grade de libertate n-k unde n este numarul de unitati observate.

Sig. Nivelul de semnificatie. Daca valoarea acestuia este mai mare de 0,05 putem accepta ipoteza egalitatii variantelor.

In exemplul considerat putem afirma ca dispersiile grupelor sunt egale deoarece nivelul de semnificatie a este 0,054.

Prezumtia de homoscedasticitate fiind respectata putem efectua testul ANOVA. Ipotezele acestuia sunt:

H₀: pentru j=1,.,k

H₁: astfel incat .

Rezultatele sunt prezentate in tabelul 4.    Primele coloane indica tipul variatiei, variatia, numarul de grade de libertate si media variatiei conform reletiilor de calcul prezentate in tabelul nr. 1. In plus in SPSS-ul returneaza si valoarea calculata a raportului F (conform relatiei ). Un nivel de semnificatie a <0,05 duce respingerea ipotezei nule.

Tabelul 4

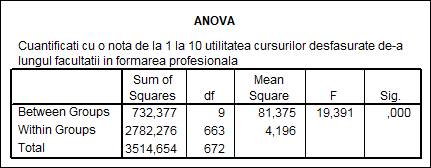
In situatia in care prezumtia de homoscedasticitate nu este indeplinita rezultatele testului ANOVA sunt neconcludente. Pentru a nu recurge la teste neparametruce vom apela la corectia Welch selectand aceasta obtiune din fereastra de definire a testului (figura nr. 1). In urma aplicarii acestei corectii (tabelul 5) obtinem valoarea calculata a statisticii testului dupa relatia 1 care se compara valoarea teoretica a distributiei F pentru numarul corectat al gradelor de libertate. Si in acest caz, daca nivelul de semnificatie a este mai mic decat 0,05 se respinge ipoteza egalitatii mediilor.

Tabelul 5

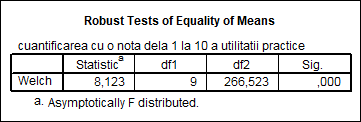
Chiar daca in urma aplicarii se respinge ipoteza egalitatii mediilor este posibil sa existe subseturi pentru care diferentele dintre medii sa nu fie semnificative. Pentru a verifica aceasta ipoteza, din fereastra de definire a testului (figura 3) se activeaza meniul Post Hoc. In figura nr. 4 este prezentata fereastra din care se pot selecta testele pe care dorim sa le utilizam in vederea realizarii comparatiilor multiple.

Figura nr. 4. Alegerea testului pentru efectuarea comparatiilor multiple

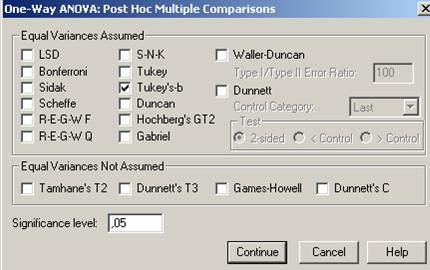
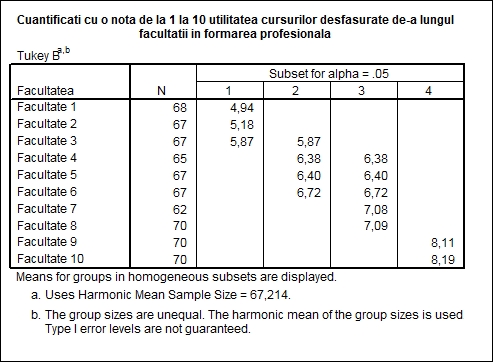
In urma efectuarii testului Tukey's s-au format 4 subseturi omogene (grupe dupa variabila factoriala pentru care este acceptata ipoteza egalitatii mediilor) prezentate in tabelul 6.

Tabelul 6