PROIECT STATISTICA

UTILIZAREA SONDAJULUI IN CARACTERIZAREA FENOMENELOR ECONOMICO-SOCIALE

0        TEMA PROIECTULUI

Un agent economic dispune de o rețea de unități economice cu profilul alimentație publică în care sunt angajați 500 de vânzători.

Pentru cei 500 de vânzători, considerați ca o colectivitate generală, s-a întocmit o bază de sondaj. Înscrierea în baza de sondaj a vânzătorilor s-a făcut în ordine alfabetică, ceea ce constituie un criteriu aleator și li s-a dat un cod (nr. crt.).

Considerând cei 500 de vânzători ca formând o colectivitate statistică se cere:

1.     să se extragă printr-un procedeu de sondaj un eșantion de 60 de unități și să se centralizeze nivelurile individuale ale fiecăruia din variabilele prezentate potrivit conținutului lor;

2.     să se grupeze datele înregistrate la punctul precedent folosind grupările simple pentru toate caracteristicile înregistrate pe intervale egale și neegale (se vor folosi minim 8 grupe pentru intervale egale și minim 3 grupe pentru intervale neegale) și să se centralizeze datele condiționate de grupările folosite. Să se reprezinte grafic seriile obținute,

3.     să se calculeze toate mărimile relative posibile și să se reprezinte grafic mărimile obținute folosind diagramele adecvate;

4.     să se calculeze indicatorii tendinței centrale, indicatorii variației și ai asimetriei pentru variabilele înregistrate;

5.     să se aplice metoda corelației și regresiei pentru datele din eșantion. Să se măsoare gradul de intensitate al corelației. Pentru date grupate se vor lua în calcul primele 10 unități din eșantion, la care se vor calcula și coeficienții de corelație a rangurilor.

1        Extragerea eșantionului

1. Din baza de sondaj se extrage un eșantion format din 60 de vânzători. La extragere s-a folosit procedeul selecției mecanice cu pas de numărare egal cu 8 și prima unitate extrasăin exemplul nostru a fost 8.

S-au înregistrat datele privind sexul, vârsta (ani), zile lucrate, ore lucrate, valoarea desfacerilor lunare (lei) și salariul net lunar (lei) din luna februarie 2009.

Interpretare..Cei 60 de vanzatori extrasi din baza de sondaj ne ofera pentru inceput urmatoarele informatii: au lucrat in total intr-o luna 1266 de zile - 10280

1.1          Gruparea datelor înregistrate

1.1.1    Gruparea pe intervale de variație egale

1.     Gruparea datelor înregistrate

1.1.  Gruparea pe intervale de variație egale

Gruparea pe intervale egale implică următoarele etape:

a)     calculul amplitudinii absolute de variației (A) care exprimă împrăștierea maximă a valorilor serei.

A^x_a = X_max – X_min;

Dacă variația este foarte mică (în cazul nostru A^x_a £ 10) se va forma o distribuție pe variante (valabil în cazul caracteristicilor: vârsta; zile lucrate).

b) stabilirea în parametrii într-un anumit număr de grupe (r) se poate stabili astfel:

Ø   dacă variația caracteristicii este relativ uniformă și volumul de unități nu este suficient de mare numărul de grupe se poate fixa anterior (din cerințele proiectului se vor folosi minimul 8 grupe pentru intervale egale);

Ø   iar dacă numărul grupelor nu este anterior cunoscut și volumul unităților este suficient de mare se recomandă stabilirea grupelor conform relației lui Sturgers,

r = 1+3,322log n

unde: n - nr. caracteristicilor.

c)determinarea mărimii intervalului de grupare (h), se calculează ca raport între amplitudinea absolută a variației și numărul de grupe:

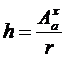sau

Notă: Mărimea intervalului (h) se rotunjește la întreg în plus (ex.3,25 4)

Prima grupă se pornește de la x_min adăugându-se succesiv mărimea intervalului de grupare (h) rezultat din calculul anterior. Valoarea din stânga intervalului va fi considerată ca limită inferioară, iar valoarea din dreapta ca limită superioară. Valorile care formează limitele intervalelor se înregistrează fie numai ca limită superioară fie ca limită inferioară pentru a evita înregistrări duble a caracteristicilor.

Analog se rezolvă pentru orice variabilă.

2A. Gruparea pe intervale egale a vânzătorilor după vârstă

a) Amplitudinea variației A^x_a = X_max – X_min = 27-19=8

Repartiția vânzătorilor după vârstă

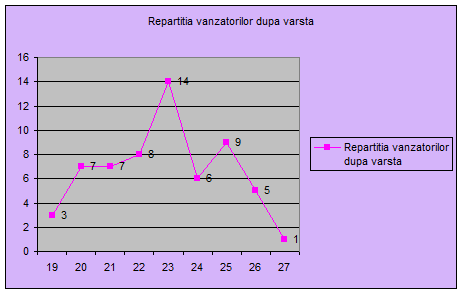
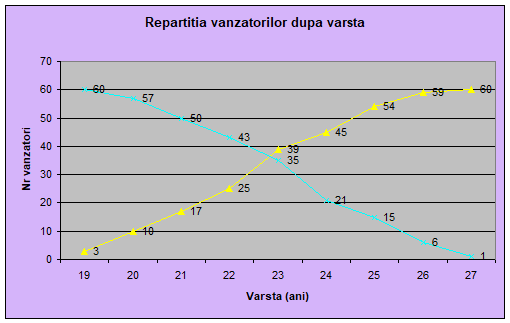
Reprezentarea grafică a repartiției vânzătorilor după vârstă se ilustrează prin poligonul frecvențelor și prin curba cumulativă a frecvențelor.

2B. Gruparea pe intervale egale a vânzătorilor după zile lucrate

a) Amplitudinea variației A^x_a = X_max – X_min = 24-17=7

Se obține o distribuție formată din   variante.

Repartiția vânzătorilor după numărul zilelor lucrate

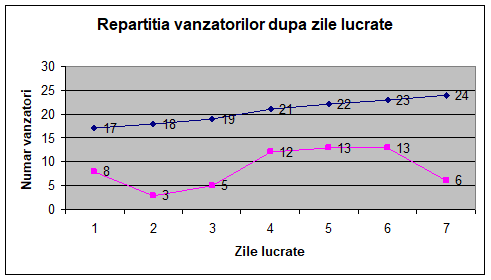
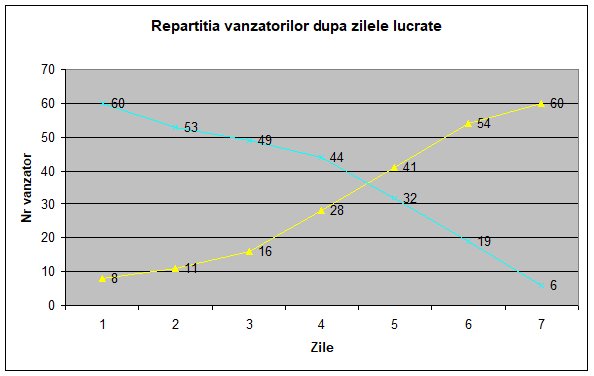
Repartizarea grafică a repartiției vânzătorilor după zilele lucrate se ilustrează prin poligonul

frecvențelor și prin curba cumulativă a frecvențelor

2C. Gruparea pe intervale egale a vânzătorilor după ore lucrate

a) Amplitudinea variației A^x_a = X_max -X_min = 211-135=76

b) Nr. de grupe r = 8

c) Mărimea intervalului h =≈ 10

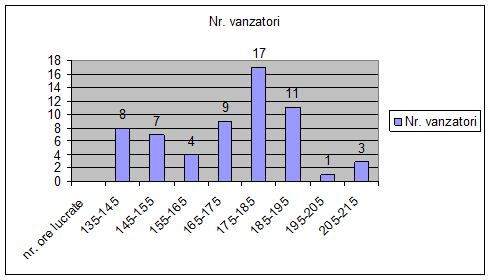
Repartiția vânzătorilor după numărul de ore lucrate

Nota: Limita superioară este inclusă în interval.

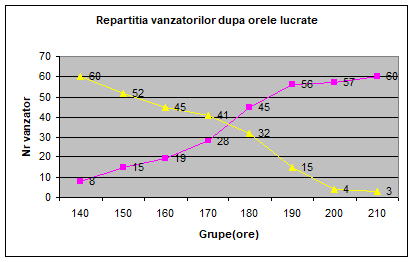
Repartizarea grafică a repartiției vânzătorilor după numărul de ore lucrate se ilustrează prin poligonl frecvențelor și prin curba cumulativă a frecvențelor.

Gruparea pe intervale egale permite structurarea colectivității pe grupe cât mai omogene, iar gruparea statistică este cea mai semnificativă modalitate a sistemetizării datelor după o caracteristică numerică sau nominativă.

Sistematizarea datelor printr-o grupare pe intervale egale răspunde necesității de sistematizare și omogenizare a datelor unei observații statistice de masă și a caracterizării independente a fiecărei variabile din propria observare.

2E. Gruparea pe intervale egale a vanzatorilor dupa salariul net

a) Amplitudinea variației A^x_a = X_max -X_min = 1846-1100=746

b) Nr. de grupe r = 8

c) Mărimea intervalului h = 746/8=93.25

Repartitia vanzatorilor in functie de salariul net lunar

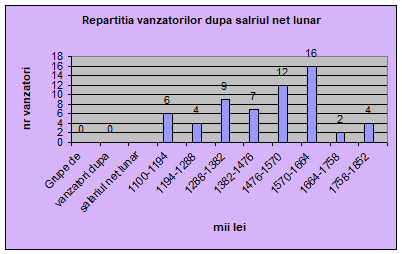
Nota: Limita inferioara este inclusa in interval.

Centralizarea valorilor dupa salariul net lunar se obtine la fel ca si la orele lucrate.

Reprezentarea grafica a repartitiei vanzatorilor dupa salariul net lunar, se poate ilustra prin histograma, poligonul frecventelor( Figura 5) si curba cumulativa a frecventelor( Figura 6).

Repartitia vanzatorilor in functie de salariul net lunar

1.1.2    Gruparea pe intervale de variație neegale

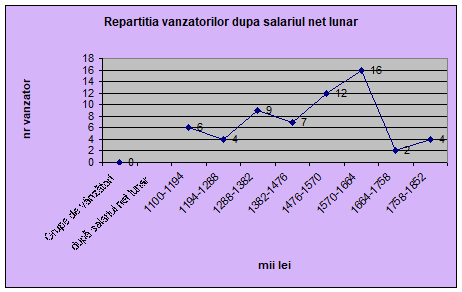
Pentru analiza structurii colectivității pe grupe tipice se folosește gruparea pe intervale neegale.

Gruparea pe intervale neegale presupune regruparea intervalelor egale.

Un prim principiu al grupării pe intervale neegale este trecerea de la variația lineară (interval de mărime constantă) la variația neuniformă a unor intervale de grupare din ce în ce mai mari.

Un alt principiu de grupare are în vedere separarea unităților pe trei grupe: mici, mijlocii și mari.

2.2.C. Gruparea pe intervale neegale a vânzătorilor după orele lucrate

Nivelul mediu 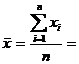   10280/60=171,33

Notă: Limita superioară inclusă în interval

2        CALCULUL MĂRIMILOR RELATIVE DE STRUCTURĂ

Din cele 5 mărimi relative întâlnite în statistică, în proiectul de față se pot determina trei:

2.1. Mărimile relative de structură se obțin ca raport între parte și întreg. Forma cea mai obișnuita de exprimare a mărimilor relative de structură este cea a procentelor care arată câte unității din indicatorul raportat revin la 100 unități ale indicatorului bază de raportare. Se pot calcula atât pe baza frecvențelor absolute și în acest caz au sens de frecvențe relative ()

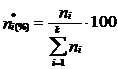
cât și pe baza valorilor centralizate privind : vârsta, zilele lucrate, orele lucrate, volumul desfacerilor și salariul net, obținându-se în acest caz ponderea sau greutatea specifică () a unei valori () în totalul valorilor colectivității ():

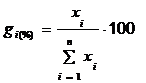
2.2. Mărimile relative de coordonare se obțin ca raport între două grupe sau între două colectivități ce coexistă în spațiu.

Pentru o colectivitate împărțită în două grupe pentru care nivelul pe grupe al variabilei studiate este x_A și x_B :

sau

Dacă sunt mai multe grupe, se alege una ca bază de comparație și se raportează, pe rând, fiecare grupă la baza aleasă.

2.3. Mărimile relative de intensitate se obțin prin raportarea a doi indicatori cu conținut diferit dar între care există o relație de interdependență.

la nivel parțial: 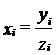; la nivelul ansamblului: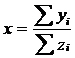

3.C Calculul mărimilor relative pe baza repartiției vânzătorilor după numărul de ore lucrate

Repartiția timpului lucrat în zile a fondului de salarii și a structurii acestora în funcție de numărul de ore lucrate

Repartiția timpului lucrat (în zile și ore), a fondului de salarii și a raportului acestora față de prima grupa, în funcție de valoarea desfacerii

Repartiția timpului lucrat (în zile și ore), a fondului de salarii pe total și în medie pe un vânzător în funcție de valoarea desfacerii

3        CARACTERIZAREA STATISTICĂ A REPARTIȚIILOR OBȚINUTE

Caracterizarea statistică în cazul dat se referă la determinarea:

a)     Indicatorilor tendinței centrale:

q      Media aritmetică

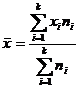
q Modul (modulul, dominanta)

q   Mediana (Me)

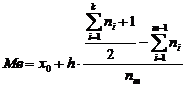
b)     Indicatorii sintetici ai variației și ai asimetriei:

q      Abaterea medie liniară :

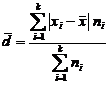
q      Dispersia

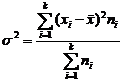
q      Abaterea medie pătratică

q        Coeficientul de variație (v):

respectiv             

q      Coeficientul de asimetrie

sau

3.1      Repartiția vânzătorilor după vârstă

a)     Calculul indicatorilor tendinței centrale:

q Media aritmetică

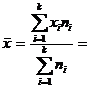
= 22.8 ani/vanz

q      Modul (modulul, dominanta)

Fiind o serie pe variante Mo este valoarea cu frecvența maximă

Mo=23 ani/vanzari                                 

q      Mediana (Me)

locul medianei: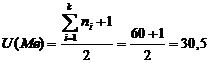

Me=23ani/vanz

b)     Calculul indicatorii sintetici ai variației și ai asimetriei

q    Dispersia

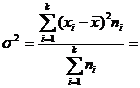
= 4,12 ani/vanz

q    Abaterea medie pătratică

q    Coeficientul de variație (v):

∙100= 8,8

v^` și v < 35% - seria este omogenă și media este reprezentativă pentru serie

q      Coeficientul de asimetrie

= -0,09

= -0.29

3.2      Repartiția vânzătorilor după zilele lucrate

a)     Calculul indicatorilor tendinței centrale:

q Media aritmetică

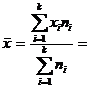
= 23,3 zile/vanz.

q      Modul (modulul, dominanta)

Fiind o serie pe variante Mo este valoarea cu frecvența maximă

q      Mediana (Me)

locul medianei: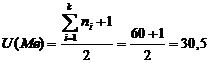

b)     Calculul indicatorii sintetici ai variației și ai asimetriei

q        Dispersia

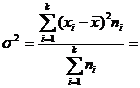
= 9,72 ani/vanz.

q    Abaterea medie pătratică

q    Coeficientul de variație (v):

∙100= 13,34

v^` și v < 35% - seria este omogenă și media este reprezentativă pentru serie

q      Coeficientul de asimetrie

= -0,09

= -0.28

Rezultă asimetrie moderată

3.3      Repartiția vânzătorilor după orele lucrate

c)     Calculul indicatorilor tendinței centrale:

q Media aritmetică

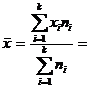
= 172 zile/vanz.

q      Modul (modulul, dominanta)

Fiind o serie pe variante Mo este valoarea cu frecvența maximă

q     

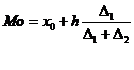
Mo= 175+10∙= 180.7 ore/vanz

q      Mediana (Me)

locul medianei: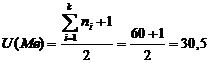

Variabila 23 ani este prima a cărei frecvență cumulată crescător este mai mare de 30,5

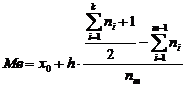= 175+ 10∙= 176.4ore/vanz

d)     Calculul indicatorii sintetici ai variației și ai asimetriei

q    Dispersia

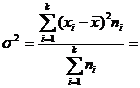
= 23,62 ani/vanz.

q    Abaterea medie pătratică

q    Coeficientul de variație (v):

∙100= 2,82

v^` și v < 35% - seria este omogenă și media este reprezentativă pentru serie

q      Coeficientul de asimetrie

= -1,79

= -2,71

Rezultă asimetrie negativa ascendenta.

Pentru interpretarea rezultatelor se vor trece indicatorii obținuți într-un tabel sintetic.

Indicatorii tendinței centrale, de variație totală și de asimetrie pentru variabilele înregistrate în eșantion.

4        ANALIZA CORELAȚIEI DINTRE VALOAREA DESFACERII ȘI SALARIU

Se aplică pentru primele 10 unități din eșantion, privind numărul de ore lucrate (x_i) și salariul net lunar (y_i ) - mii lei. Seria se va ordona crescător după numărul de ore lucrate (x_i) menținându-se salariul net lunar (y_i ) corespunzător.

Dintre metodele simple de cercetare a legaturilor statistice recurgem la :

A)     Metoda seriilor paralele interdependente

Concluzie: Valorile x_i fiind ordonate crescător se poate observa că și valorile y_i cresc în cea mai mare parte, ceea ce sugerează o legătură directă.

B)     Metoda grafică este o altă cale de a stabili legătura dintre fenomene.

Pentru a obține graficul de corelație, denumit și corelograma, valorile caracteristicii factoriale (x_i) sau intervalele acesteia se trec pe abscisa, iar pe ordonate valorile caracteristicii rezultative (y_i) sau intervalele respective. Fiecare unitate observată a celor două caracteristici se reprezintă grafic printr-un punct.

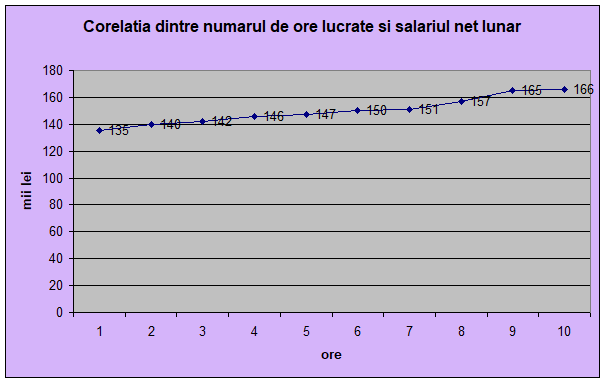
Graficul de asemenea confirmă o legătură directă de formă liniară.

Metoda grafica este utilizată cu bune rezultate pentru alegerea funcției analitice care se studiază (în cazul regresiei și corelației)

Metodele de studiere a legaturilor prezentate anterior au ca deficiență principală faptul că deși permit constatarea legăturii și caracterulul ei, nu o pot măsura printr-un indicator sintetic. Acest inconvenient este înlăturat prin utilizarea metodei regresie.

Metoda regresiei constituie o metoda statistică analitică de cercetare a legăturii dintre variabile cu ajutorul unor funcții denumite funcții de regresie.

Notând cu Y variabile dependenta și cu x₁ , x₂ x_n variabilele independente obținem ecuația de regresie y = f (x₁ , x₂ x_n).

În cazul de fata am apelat la modelul de regresie unifactorială liniar considerând legătura dintre y și x de tipul y_xi = a +bx_i. Parametri ecuației în acest caz se determină prin rezolvarea următorului sistem de ecuații:

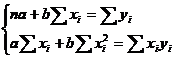
Dacă se folosește metoda determinanților se obține:

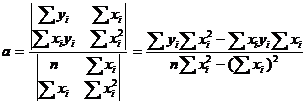
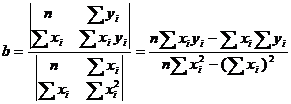
Datele necesare calculării celor doi parametri sunt prezentate în tabelul de mai jos.

Funcția de regresie este: y_xi = a +bx_i

Intensitatea legăturii se măsoară prin coeficientul de corelație (r_y/x).

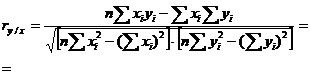
Interpretare…

Rezulta ca legatura dintre aceste 2 variabile este directa si puternica.

5        BIBLIOGRAFIE

1. Elena-Maria Biji, Eugenia Lilea, Mihaela Vătui, Emilia Gogu, STATISTICĂ APLICATĂ ÎN ECONOMIE, Editura Oscar Print, 2007

2. . Elena-Maria Biji, Eugenia Lilea, Mihaela Vătui, Emilia Gogu, APLICAȚII STATISTICE ÎN STUDIUL FENOMENELOR ECONOMICE, Editura Oscar Print, București 2007